沪科版九年级上册数学第一次月考试卷(含答案)
文档属性
| 名称 | 沪科版九年级上册数学第一次月考试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 460.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 15:20:40 | ||
图片预览


文档简介
沪科版九年级上册数学第一次月考试题
一、选择题。(每小题只有一个正确答案,每小题3分,共30分)
1.下列函数是二次函数的是( )
A. B. C. D.
2.将抛物线y=2x2向右平移1个单位,得到的抛物线是( )
A.y=2x2+1 B.y=2x2﹣1 C.y=2(x+1) D.y=2(x﹣1)2
3.共享单车为市民出行带来了方便,某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,设该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )
A.y=x2+a B.y=a(1+x)2 C.y=(1﹣x)2+a D.y=a(1﹣x)2
4.在平面直角坐标系xOy中,抛物线的顶点坐标是( )
A.(2,-1) B.(-1,-1) C.(1,1) D.(1,-1)
5.若函数的图象与坐标轴有三个交点,则b的取值范围是
A.且 B. C. D.
6.下列二次函数的图象中,其对称轴是x=1的为( )
A.y=x2+2x B.y=x2﹣2x C.y=x2﹣2 D.y=x2﹣4x
7.中国贵州省内的射电望远镜()是目前世界上口径最大,精度最高的望远镜,根据有关资料显示,该望远镜的轴截面呈现抛物线状,口径为500米,最低点到口径面的距离是100米,若按如图(2)建立平面直角坐标系,则抛物线的解析式是( )
A. B. C. D.
8.某同学在利用描点法画二次函数y=ax2+bx+c(a=0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x … 0 1 2 3 4 …
y … ﹣3 0 ﹣1 0 ﹣3 …
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A. B. C. D.
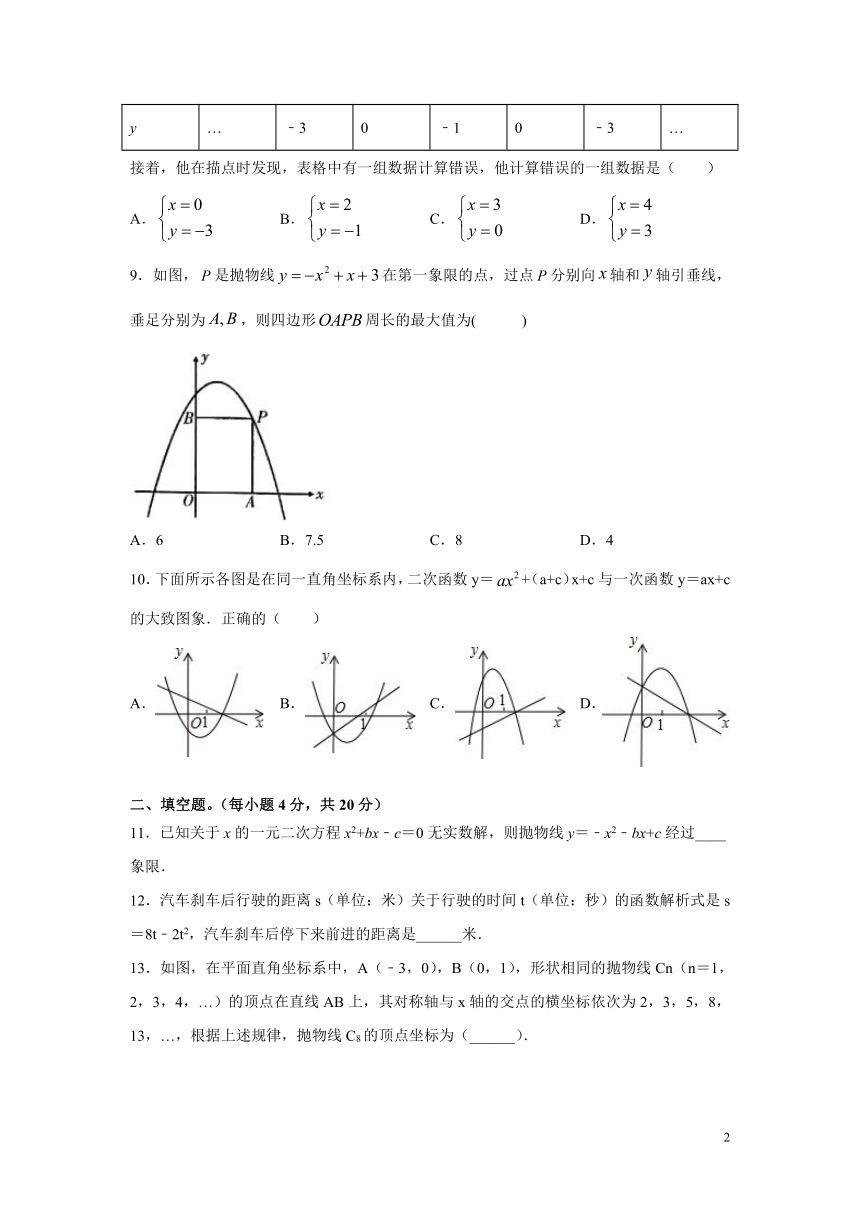
9.如图,是抛物线在第一象限的点,过点分别向轴和轴引垂线,垂足分别为,则四边形周长的最大值为( )
A.6 B.7.5 C.8 D.4
10.下面所示各图是在同一直角坐标系内,二次函数y=+(a+c)x+c与一次函数y=ax+c的大致图象.正确的( )
A. B. C. D.
二、填空题。(每小题4分,共20分)
11.已知关于x的一元二次方程x2+bx﹣c=0无实数解,则抛物线y=﹣x2﹣bx+c经过____象限.
12.汽车刹车后行驶的距离s(单位:米)关于行驶的时间t(单位:秒)的函数解析式是s=8t﹣2t2,汽车刹车后停下来前进的距离是______米.
13.如图,在平面直角坐标系中,A(﹣3,0),B(0,1),形状相同的抛物线Cn(n=1,2,3,4,…)的顶点在直线AB上,其对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…,根据上述规律,抛物线C8的顶点坐标为(______).
14.在直角坐标系中,点的坐标为,若抛物线与线段有且只有一个公共点,则的取值范围为______.
15.二次函数的图象如图,则_______0.(填“>”“<”或“=”)
三、解答题。(共70分)
16.(6分)已知二次函数,求顶点坐标,小明的计算结果与其他同学的不同,请你帮他检查一个,在标出的①②③④几个步骤中开始出现错误的是____步,请写出此题正确的求顶点的计算过程.
小明的计算过程:
① ;
② ;
③ ;
∴顶点坐标是 ④ ;
17.(9分)已知二次函数y=x2﹣2x﹣1.
x … ﹣1 0 1 2 3 …
y … …
(1)请在表内的空格中填入适当的数;
(2)根据列表,请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象;
(3)当x在什么范围内时,y随x增大而减小;
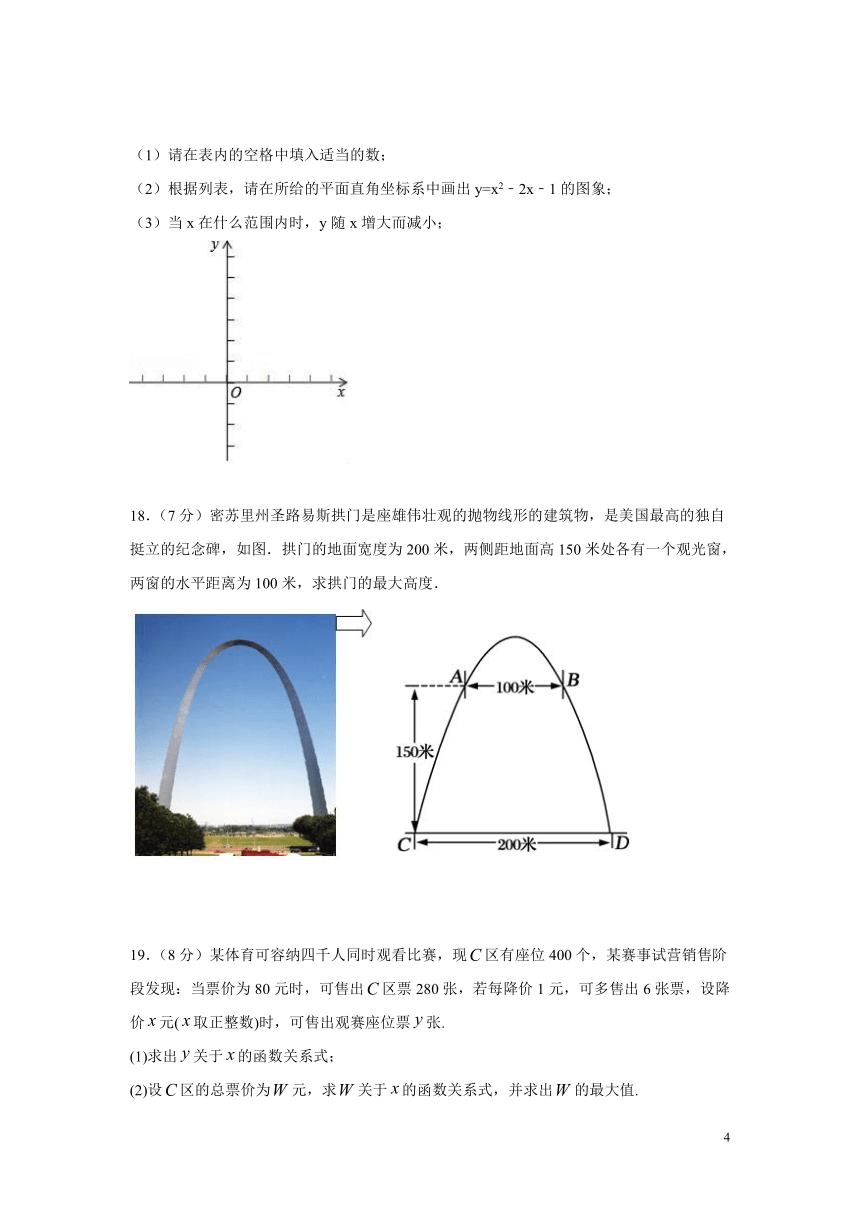
18.(7分)密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.
19.(8分)某体育可容纳四千人同时观看比赛,现区有座位400个,某赛事试营销售阶段发现:当票价为80元时,可售出区票280张,若每降价1元,可多售出6张票,设降价元(取正整数)时,可售出观赛座位票张.
(1)求出关于的函数关系式;
(2)设区的总票价为元,求关于的函数关系式,并求出的最大值.
20.(6分)阿波罗尼奥斯(Apollonius of Perga,约公元前262-190年),古希腊数学家,与欧几里得,阿基米德齐名,他的著作《圆锥曲线论》是古代世界光辉的科学成果.
材料:《圆锥曲线论》里面对抛物线的定义:平面内一个动点到一个定点与一条定直线的距离之比等于1,或者说:平面内一动点到一定点与一条直线的距离相等的轨迹就是抛物线.
问题:已知点,,直线,连接,若点到直线的距离与的长相等,请求出与的关系式.
解:如图,∵,,
∴
∵,直线,
∴点到直线的距离为
∵点到直线的距离与的长相等,
∴,
平方化简得,.
若将上述问题中点坐标改为,直线变为,按照问题解题思路,试求出与的关系式,并在平面直角坐标系中利用描点法画出其图象,你能发现什么?
21.(8分)如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了46米木栏.
(1)若a=26,所围成的矩形菜园的面积为280平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
22.(9分)对于某一函数给出如下定义:对于任意实数,当自变量时,函数关于的函数图象为,将沿直线翻折后得到的函数图象为,函数的图象由和两部分共同组成,则函数为原函数的“对折函数”,如函数()的对折函数为
(1)求函数()的对折函数;
(2)若点在函数()的对折函数的图象上,求的值;
(3)当函数()的对折函数与轴有不同的交点个数时,直接写出的取值范围.
23.(8分)已知二次函数y=x2﹣4x+3,
(1)画出它的图象,并求出它的的顶点坐标和对称轴;
(2)当函数值y>0时,观察图象,直接写出自变量x的取值范围.
24.(9分)如图,一次函数的图象和反比例函数的图象相交于两点.
(1)试确定一次函数与反比例函数的解析式;
(2)求的面积;
(3)结合图象,直接写出使成立的的取值范围.
参考答案
1.C
2.D
3.B
4.D
5.A
6.B
7.A
8.B
9.C
10.D
11.三、四.
12.8
13.(55,).
14.或
15.>
16.①;正确过程见解析.
17.(1)填表见解析;(2)图象见解析. (3)由函数图象可知抛物线的对称轴为x=1,当x<1时,y随x的增大而减小.
18.200米.
19.(1);(2) ;当时,元.
20.,图象见解析;该图象为开口向右的抛物线.
21.(1)20m;
(2)当a≥24时, S最大值为288平方米;当0<a<24时, S最大值为.
22.(1);(2)或-6;(3)n<-1时,与x轴有4个交点,n=-1时,与x轴有3个交点;与x轴有2个交点;n=3时,与x轴有3个交点;n>3时,与x轴无交点.
23.(1)画图见解析;顶点坐标为(2,﹣1),对称轴为x=2
(2)x<1或x>3
24.(1)反比例函数的解析式为,一次函数的解析式为;(2)8;(3)或.
(
2
)
(
1
)
一、选择题。(每小题只有一个正确答案,每小题3分,共30分)
1.下列函数是二次函数的是( )
A. B. C. D.
2.将抛物线y=2x2向右平移1个单位,得到的抛物线是( )
A.y=2x2+1 B.y=2x2﹣1 C.y=2(x+1) D.y=2(x﹣1)2
3.共享单车为市民出行带来了方便,某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,设该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )
A.y=x2+a B.y=a(1+x)2 C.y=(1﹣x)2+a D.y=a(1﹣x)2
4.在平面直角坐标系xOy中,抛物线的顶点坐标是( )
A.(2,-1) B.(-1,-1) C.(1,1) D.(1,-1)
5.若函数的图象与坐标轴有三个交点,则b的取值范围是
A.且 B. C. D.
6.下列二次函数的图象中,其对称轴是x=1的为( )
A.y=x2+2x B.y=x2﹣2x C.y=x2﹣2 D.y=x2﹣4x
7.中国贵州省内的射电望远镜()是目前世界上口径最大,精度最高的望远镜,根据有关资料显示,该望远镜的轴截面呈现抛物线状,口径为500米,最低点到口径面的距离是100米,若按如图(2)建立平面直角坐标系,则抛物线的解析式是( )
A. B. C. D.
8.某同学在利用描点法画二次函数y=ax2+bx+c(a=0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x … 0 1 2 3 4 …
y … ﹣3 0 ﹣1 0 ﹣3 …
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A. B. C. D.
9.如图,是抛物线在第一象限的点,过点分别向轴和轴引垂线,垂足分别为,则四边形周长的最大值为( )
A.6 B.7.5 C.8 D.4
10.下面所示各图是在同一直角坐标系内,二次函数y=+(a+c)x+c与一次函数y=ax+c的大致图象.正确的( )
A. B. C. D.
二、填空题。(每小题4分,共20分)
11.已知关于x的一元二次方程x2+bx﹣c=0无实数解,则抛物线y=﹣x2﹣bx+c经过____象限.
12.汽车刹车后行驶的距离s(单位:米)关于行驶的时间t(单位:秒)的函数解析式是s=8t﹣2t2,汽车刹车后停下来前进的距离是______米.
13.如图,在平面直角坐标系中,A(﹣3,0),B(0,1),形状相同的抛物线Cn(n=1,2,3,4,…)的顶点在直线AB上,其对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…,根据上述规律,抛物线C8的顶点坐标为(______).
14.在直角坐标系中,点的坐标为,若抛物线与线段有且只有一个公共点,则的取值范围为______.
15.二次函数的图象如图,则_______0.(填“>”“<”或“=”)
三、解答题。(共70分)
16.(6分)已知二次函数,求顶点坐标,小明的计算结果与其他同学的不同,请你帮他检查一个,在标出的①②③④几个步骤中开始出现错误的是____步,请写出此题正确的求顶点的计算过程.
小明的计算过程:
① ;
② ;
③ ;
∴顶点坐标是 ④ ;
17.(9分)已知二次函数y=x2﹣2x﹣1.
x … ﹣1 0 1 2 3 …
y … …
(1)请在表内的空格中填入适当的数;
(2)根据列表,请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象;
(3)当x在什么范围内时,y随x增大而减小;
18.(7分)密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.
19.(8分)某体育可容纳四千人同时观看比赛,现区有座位400个,某赛事试营销售阶段发现:当票价为80元时,可售出区票280张,若每降价1元,可多售出6张票,设降价元(取正整数)时,可售出观赛座位票张.
(1)求出关于的函数关系式;
(2)设区的总票价为元,求关于的函数关系式,并求出的最大值.
20.(6分)阿波罗尼奥斯(Apollonius of Perga,约公元前262-190年),古希腊数学家,与欧几里得,阿基米德齐名,他的著作《圆锥曲线论》是古代世界光辉的科学成果.
材料:《圆锥曲线论》里面对抛物线的定义:平面内一个动点到一个定点与一条定直线的距离之比等于1,或者说:平面内一动点到一定点与一条直线的距离相等的轨迹就是抛物线.
问题:已知点,,直线,连接,若点到直线的距离与的长相等,请求出与的关系式.
解:如图,∵,,
∴
∵,直线,
∴点到直线的距离为
∵点到直线的距离与的长相等,
∴,
平方化简得,.
若将上述问题中点坐标改为,直线变为,按照问题解题思路,试求出与的关系式,并在平面直角坐标系中利用描点法画出其图象,你能发现什么?
21.(8分)如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了46米木栏.
(1)若a=26,所围成的矩形菜园的面积为280平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
22.(9分)对于某一函数给出如下定义:对于任意实数,当自变量时,函数关于的函数图象为,将沿直线翻折后得到的函数图象为,函数的图象由和两部分共同组成,则函数为原函数的“对折函数”,如函数()的对折函数为
(1)求函数()的对折函数;
(2)若点在函数()的对折函数的图象上,求的值;
(3)当函数()的对折函数与轴有不同的交点个数时,直接写出的取值范围.
23.(8分)已知二次函数y=x2﹣4x+3,
(1)画出它的图象,并求出它的的顶点坐标和对称轴;
(2)当函数值y>0时,观察图象,直接写出自变量x的取值范围.
24.(9分)如图,一次函数的图象和反比例函数的图象相交于两点.
(1)试确定一次函数与反比例函数的解析式;
(2)求的面积;
(3)结合图象,直接写出使成立的的取值范围.
参考答案
1.C
2.D
3.B
4.D
5.A
6.B
7.A
8.B
9.C
10.D
11.三、四.
12.8
13.(55,).
14.或
15.>
16.①;正确过程见解析.
17.(1)填表见解析;(2)图象见解析. (3)由函数图象可知抛物线的对称轴为x=1,当x<1时,y随x的增大而减小.
18.200米.
19.(1);(2) ;当时,元.
20.,图象见解析;该图象为开口向右的抛物线.
21.(1)20m;
(2)当a≥24时, S最大值为288平方米;当0<a<24时, S最大值为.
22.(1);(2)或-6;(3)n<-1时,与x轴有4个交点,n=-1时,与x轴有3个交点;与x轴有2个交点;n=3时,与x轴有3个交点;n>3时,与x轴无交点.
23.(1)画图见解析;顶点坐标为(2,﹣1),对称轴为x=2
(2)x<1或x>3
24.(1)反比例函数的解析式为,一次函数的解析式为;(2)8;(3)或.
(
2
)
(
1
)
同课章节目录
