沪科版九年级上册数学第一次月考试题(含答案)
文档属性
| 名称 | 沪科版九年级上册数学第一次月考试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 198.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 00:00:00 | ||
图片预览


文档简介
沪科版九年级上册数学第一次月考试题
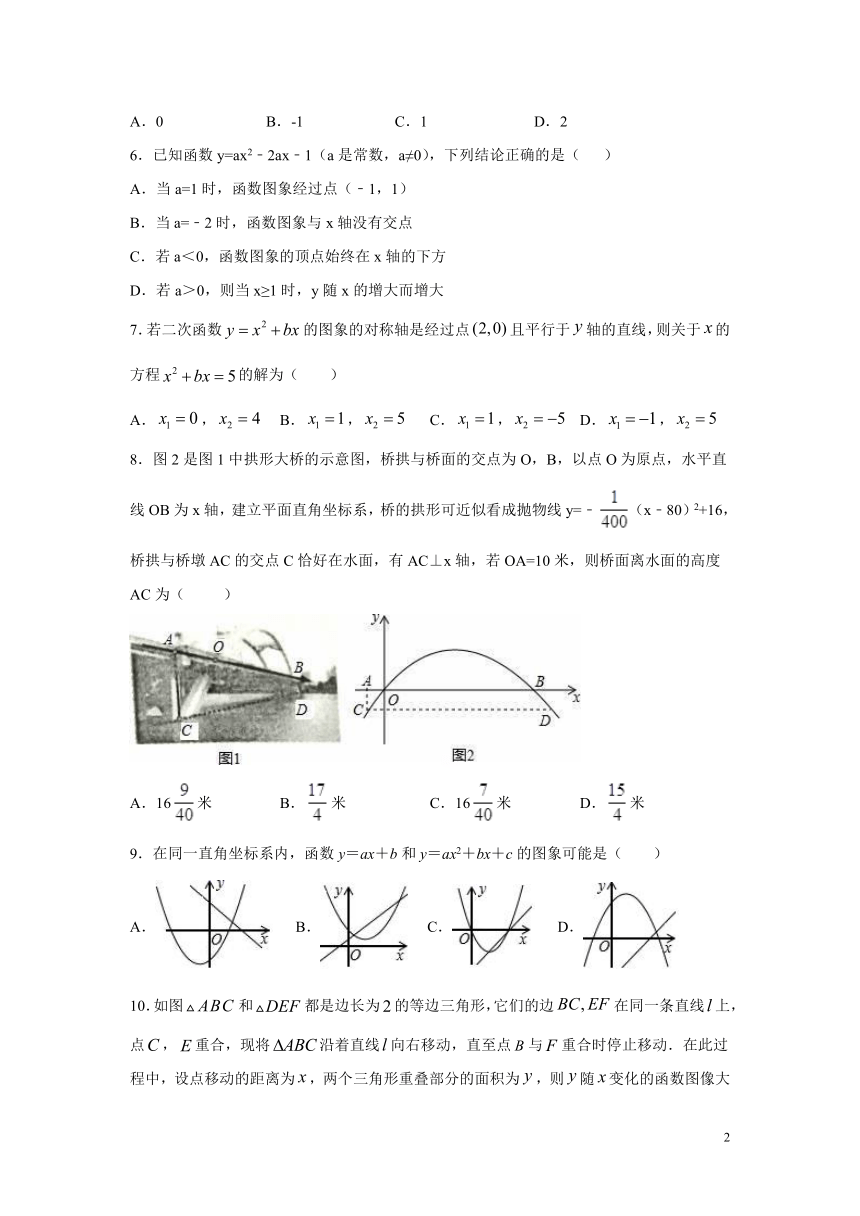
一、选择题。(每小题只有一个正确答案,每小题3分,共30分)
1.函数y=﹣x2﹣4x﹣3图象顶点坐标是( )
A.(2,﹣1) B.(﹣2,1) C.(﹣2,﹣1) D.(2,1)
2.将函数y=x2+x的图象向右平移a(a>0)个单位,得到函数y=x2-3x+2的图象,则a的值为( )
A.1 B.2 C.3 D.4
3.如图,已知反比例函数y=(x>0),则k的范围是( )
A.14.如图,正的顶点A在反比例函数(x>0)的图象上,则点B的坐标为( )
A.(2,0) B.(,0) C.(2,0) D.(,0)
5.如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a-b+c的值为( )
A.0 B.-1 C.1 D.2
6.已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象经过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a<0,函数图象的顶点始终在x轴的下方
D.若a>0,则当x≥1时,y随x的增大而增大
7.若二次函数的图象的对称轴是经过点且平行于轴的直线,则关于的方程的解为( )
A., B., C., D.,
8.图2是图1中拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线y=﹣(x﹣80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为( )
A.16米 B.米 C.16米 D.米
9.在同一直角坐标系内,函数y=ax+b和y=ax2+bx+c的图象可能是( )
A. B. C. D.
10.如图和都是边长为的等边三角形,它们的边在同一条直线上,点,重合,现将沿着直线向右移动,直至点与重合时停止移动.在此过程中,设点移动的距离为,两个三角形重叠部分的面积为,则随变化的函数图像大致为( )
A. B.
C. D.
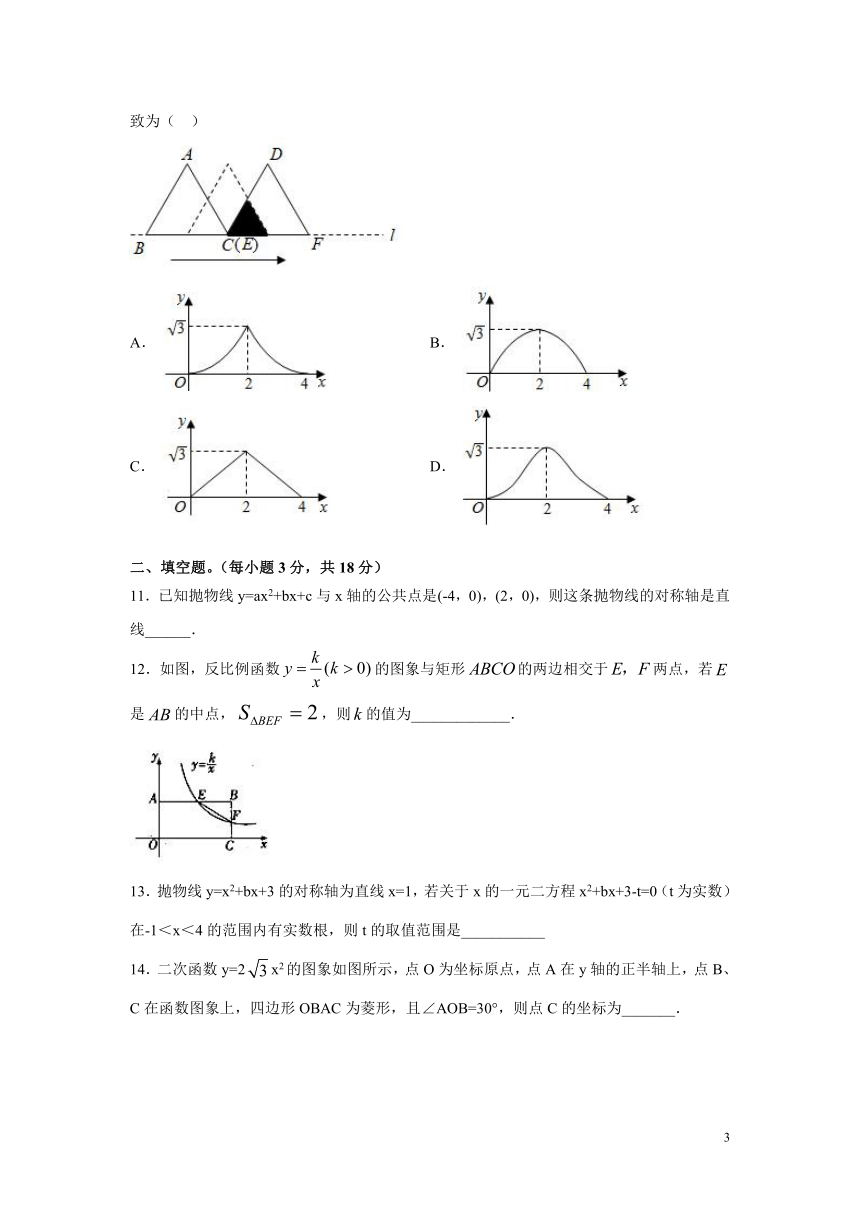
二、填空题。(每小题3分,共18分)
11.已知抛物线y=ax2+bx+c与x轴的公共点是(-4,0),(2,0),则这条抛物线的对称轴是直线______.
12.如图,反比例函数的图象与矩形的两边相交于两点,若是的中点,,则的值为_____________.
13.抛物线y=x2+bx+3的对称轴为直线x=1,若关于x的一元二方程x2+bx+3-t=0(t为实数)在-1<x<4的范围内有实数根,则t的取值范围是___________
14.二次函数y=2x2的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B、C在函数图象上,四边形OBAC为菱形,且∠AOB=30°,则点C的坐标为_______.
15.已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:①abc<0;②b2﹣4ac>0;③3a+c>0;④(a+c)2<b2其中正确的结论有______(填序号).
16.若二次函数y=a(x+h)2+k的图象经过(-3,0),(5,0)两点,则h的值为________.
三、解答题。(共72分)
17.(6分)已知二次函数的顶点坐标为(2,4),且其图像与x轴的交点在正方向3个单位处,求此二次函数的解析式.
18.(8分)如图,D为反比例函数的图象上一点,过D作DE⊥x轴于点E,DC⊥y轴于点C,一次函数y=-x+2的图象经过C点,与x轴相交于A点,四边形DCAE的面积为4,求k的值.
19.(8分)如图所示,某建筑物有一抛物线形的大门,小强想知道这道门的高度.他先测出门的宽度AB=8 m,然后用一根长为4 m的小竹竿CD竖直地接触地面和门的内壁,并测得AC=1 m.小强画出了如图的草图,请你帮他算一算门的高度OE(精确到0.1 m).
20.(8分)已知二次函数y=ax2+bx+c中,函数值y与自变量x的部分对应值如下表:
x … -1 0 1 2 3 4 …
y … 10 5 2 1 2 5 …
(1)求该二次函数的表达式;
(2)当x为何值时,y有最小值,最小值是多少?
21.(8分)在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A(-2,0),B(4,0)两点,交y轴于点C,点P是第四象限内抛物线上的一个动点.
(1)求二次函数的解析式;
(2)如图,连接AC,PA,PC,若S△PAC=,求点P的坐标;
22.(8分)有一个抛物线形的拱形隧道,隧道的最大高度为6m,跨度为8m,把它放在如图所示的平面直角坐标系中.
求这条抛物线所对应的函数关系式;
若要在隧道壁上点如图安装一盏照明灯,灯离地面高求灯与点B的距离.
23.(9分)如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图像和反比例函数的图像的两个交点
(1)求反比例函数和一次函数的解析式
(2)求直线与x轴的交点C的坐标及△AOB的面积
(3)当x取何值时,y1=y2;当x取何值时,y1>y2
24.(9分)新冠肺炎严重影响了企业生产销售,为此,六安市政府根据企业的实际情况决定对其进行财政支持.某企业在销售某种进价为600元/台的家用“消毒柜”时.经过市场销售后发现:在一个月内,当售价是700元/台时,可售出350台,且售价每提高10元,就会少售出5台.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;
(2)请计算当售价x(元台)定为多少时,该商场每月销售这种“空气清洁器”所获得的利润W(元)最大?最大利润是多少?
(3)若政府根据企业的经营产品,将销售“消毒柜”纳入民生工程项目,规定:每销售一台“消毒柜”,财政补贴商家200元,但销售利润不能高于进价的25%,请问:该商场想获取最大利润,是否参与竞标此民生工程项目?并说明理由.
25.(8分)如果二次函数的二次项系数为l,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3]
(1)若一个函数的特征数为[﹣2,1],求此函数图象的顶点坐标.
(2)探究下列问题:
①若一个函数的特征数为[4,﹣1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
参考答案
1.B
2.B
3.C
4.A
5.A
6.D
7.D
8.B
9.C
10.A
11.x=-1.
12.8
13.2≤t<11
14.(﹣)
15.②④
16.-1
17.
18.-2
19.门的高度约为9.1m
20.(1)y=(x-2)2+1.(2)当x=2时,y有最小值1.
21.(1); (2)
22.; 照明灯与点B的距离为.
23.(1)y2=,y1=-x-2;(2)6;(3)x=-4或x=2;x<-4或0<x<2
24.(1);(2)当时,;(3)该商场想获取最大利润,会参与竞标此民生工程项目.
25.(1)(1,0);(2)①[2,﹣3];②原函数的图象向左平移个单位,再向下平移个单位得到.
(
2
)
(
1
)
一、选择题。(每小题只有一个正确答案,每小题3分,共30分)
1.函数y=﹣x2﹣4x﹣3图象顶点坐标是( )
A.(2,﹣1) B.(﹣2,1) C.(﹣2,﹣1) D.(2,1)
2.将函数y=x2+x的图象向右平移a(a>0)个单位,得到函数y=x2-3x+2的图象,则a的值为( )
A.1 B.2 C.3 D.4
3.如图,已知反比例函数y=(x>0),则k的范围是( )
A.1
A.(2,0) B.(,0) C.(2,0) D.(,0)
5.如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a-b+c的值为( )
A.0 B.-1 C.1 D.2
6.已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象经过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a<0,函数图象的顶点始终在x轴的下方
D.若a>0,则当x≥1时,y随x的增大而增大
7.若二次函数的图象的对称轴是经过点且平行于轴的直线,则关于的方程的解为( )
A., B., C., D.,
8.图2是图1中拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线y=﹣(x﹣80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为( )
A.16米 B.米 C.16米 D.米
9.在同一直角坐标系内,函数y=ax+b和y=ax2+bx+c的图象可能是( )
A. B. C. D.
10.如图和都是边长为的等边三角形,它们的边在同一条直线上,点,重合,现将沿着直线向右移动,直至点与重合时停止移动.在此过程中,设点移动的距离为,两个三角形重叠部分的面积为,则随变化的函数图像大致为( )
A. B.
C. D.
二、填空题。(每小题3分,共18分)
11.已知抛物线y=ax2+bx+c与x轴的公共点是(-4,0),(2,0),则这条抛物线的对称轴是直线______.
12.如图,反比例函数的图象与矩形的两边相交于两点,若是的中点,,则的值为_____________.
13.抛物线y=x2+bx+3的对称轴为直线x=1,若关于x的一元二方程x2+bx+3-t=0(t为实数)在-1<x<4的范围内有实数根,则t的取值范围是___________
14.二次函数y=2x2的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B、C在函数图象上,四边形OBAC为菱形,且∠AOB=30°,则点C的坐标为_______.
15.已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:①abc<0;②b2﹣4ac>0;③3a+c>0;④(a+c)2<b2其中正确的结论有______(填序号).
16.若二次函数y=a(x+h)2+k的图象经过(-3,0),(5,0)两点,则h的值为________.
三、解答题。(共72分)
17.(6分)已知二次函数的顶点坐标为(2,4),且其图像与x轴的交点在正方向3个单位处,求此二次函数的解析式.
18.(8分)如图,D为反比例函数的图象上一点,过D作DE⊥x轴于点E,DC⊥y轴于点C,一次函数y=-x+2的图象经过C点,与x轴相交于A点,四边形DCAE的面积为4,求k的值.
19.(8分)如图所示,某建筑物有一抛物线形的大门,小强想知道这道门的高度.他先测出门的宽度AB=8 m,然后用一根长为4 m的小竹竿CD竖直地接触地面和门的内壁,并测得AC=1 m.小强画出了如图的草图,请你帮他算一算门的高度OE(精确到0.1 m).
20.(8分)已知二次函数y=ax2+bx+c中,函数值y与自变量x的部分对应值如下表:
x … -1 0 1 2 3 4 …
y … 10 5 2 1 2 5 …
(1)求该二次函数的表达式;
(2)当x为何值时,y有最小值,最小值是多少?
21.(8分)在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A(-2,0),B(4,0)两点,交y轴于点C,点P是第四象限内抛物线上的一个动点.
(1)求二次函数的解析式;
(2)如图,连接AC,PA,PC,若S△PAC=,求点P的坐标;
22.(8分)有一个抛物线形的拱形隧道,隧道的最大高度为6m,跨度为8m,把它放在如图所示的平面直角坐标系中.
求这条抛物线所对应的函数关系式;
若要在隧道壁上点如图安装一盏照明灯,灯离地面高求灯与点B的距离.
23.(9分)如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图像和反比例函数的图像的两个交点
(1)求反比例函数和一次函数的解析式
(2)求直线与x轴的交点C的坐标及△AOB的面积
(3)当x取何值时,y1=y2;当x取何值时,y1>y2
24.(9分)新冠肺炎严重影响了企业生产销售,为此,六安市政府根据企业的实际情况决定对其进行财政支持.某企业在销售某种进价为600元/台的家用“消毒柜”时.经过市场销售后发现:在一个月内,当售价是700元/台时,可售出350台,且售价每提高10元,就会少售出5台.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;
(2)请计算当售价x(元台)定为多少时,该商场每月销售这种“空气清洁器”所获得的利润W(元)最大?最大利润是多少?
(3)若政府根据企业的经营产品,将销售“消毒柜”纳入民生工程项目,规定:每销售一台“消毒柜”,财政补贴商家200元,但销售利润不能高于进价的25%,请问:该商场想获取最大利润,是否参与竞标此民生工程项目?并说明理由.
25.(8分)如果二次函数的二次项系数为l,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3]
(1)若一个函数的特征数为[﹣2,1],求此函数图象的顶点坐标.
(2)探究下列问题:
①若一个函数的特征数为[4,﹣1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
参考答案
1.B
2.B
3.C
4.A
5.A
6.D
7.D
8.B
9.C
10.A
11.x=-1.
12.8
13.2≤t<11
14.(﹣)
15.②④
16.-1
17.
18.-2
19.门的高度约为9.1m
20.(1)y=(x-2)2+1.(2)当x=2时,y有最小值1.
21.(1); (2)
22.; 照明灯与点B的距离为.
23.(1)y2=,y1=-x-2;(2)6;(3)x=-4或x=2;x<-4或0<x<2
24.(1);(2)当时,;(3)该商场想获取最大利润,会参与竞标此民生工程项目.
25.(1)(1,0);(2)①[2,﹣3];②原函数的图象向左平移个单位,再向下平移个单位得到.
(
2
)
(
1
)
同课章节目录
