沪科版九年级上册数学第一次月考试题(含答案)
文档属性
| 名称 | 沪科版九年级上册数学第一次月考试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 235.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 15:23:35 | ||
图片预览


文档简介
沪科版九年级上册数学第一次月考试题
一、选择题。(每小题只有一个正确答案,每小题3分,共30分)
1.下列函数一定是关于x的二次函数的是( )
A. B.
C. D.
2.将抛物线向上平移两个单位长度,再向右平移一个单位长度后,得到的物物线解析式是( )
A. B.
C. D.
3.抛物线与坐标轴的交点个数为( )
A.0 B.1 C.2 D.3
4.如图所示,反比例函数y=(k≠0,x>0)的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为8,则k的值为( )
A. B.2 C.2 D.2
5.若二次函数,当时,随的增大而减小,则的取值范围是( )
A. B. C. D.
6.若抛物线()恒在轴下方,则常数应满足( )
A. B.
C. D.
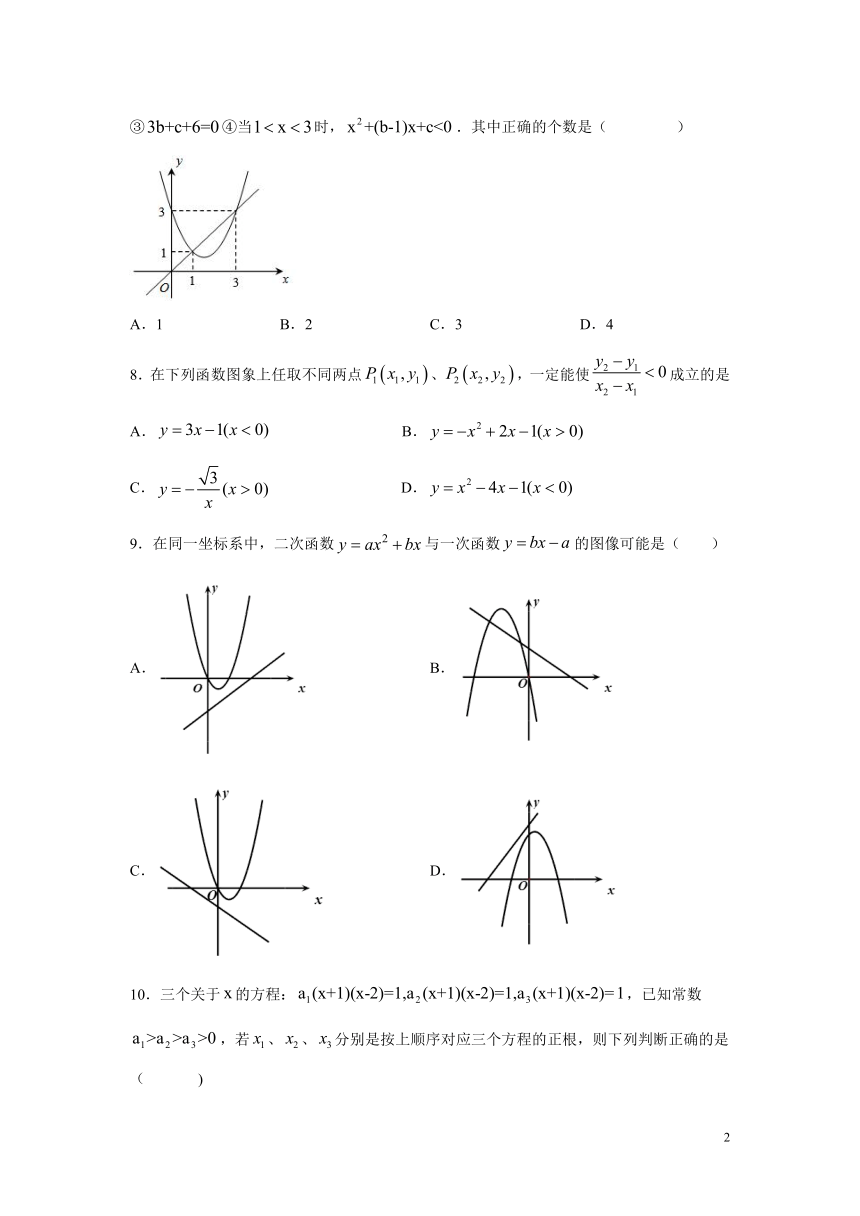
7.函数与的图象如图所示,有以下结论:① ② ③④当时,.其中正确的个数是( )
A.1 B.2 C.3 D.4
8.在下列函数图象上任取不同两点、,一定能使成立的是
A. B.
C. D.
9.在同一坐标系中,二次函数与一次函数的图像可能是( )
A. B.
C. D.
10.三个关于的方程:,已知常数,若、、分别是按上顺序对应三个方程的正根,则下列判断正确的是( )
A. B.
C. D.不能确定的大小
二、填空题。(每小题4分,共16分)
11.若(-2,5)、(4,5)是抛物线上的两点,则它的对称轴是_____________.
12.二次函数的图象绕其顶点旋转180°后所得图像的解析式是_____________.
13.二次函数,当时,的取值范围是_____________.
14.如图,点在双曲线上,且点A的横坐标为3,过作⊥轴,垂足为,的垂直平分线交于,则的面积为________________.
三、解答题。(共74分)
15.(8分)已知二次函数的图象经过点(0,0),且它的顶点坐标是(1,-2).
(1)求这个二次函数的表达式;
(2)判断点(3,5)是否在这个二次函数的图像上,并说明理由.
16.(6分)用配方法将二次函数转化为顶点式,并写出其对称轴和顶点坐标.
17.(8分)已知抛物线交y轴于负半轴,且与轴有两个不同的交点.
(1)求c的取值范围;
(2)若抛物线经过点、点和点,试比较的大小.
18.(8分)二次函数y=a(x-h)2的图象如图,已知a=,OA=OC,试求该抛物线的解析式.
19.(8分)如图,在平面直角坐标系中,已知点B(4,0),等腰直角三角形的直角顶点在反比例函数的图象上.
(1)求反比例函数的表达式;
(2)把向右平移个单位长度,对应得到.当这个函数图象经过一边的中点时,求的值.
20.(8分)有一个抛物线形的单向道路隧道,隧道离地面的最大高度为4m,跨度为10m,把它放在图示平面直角坐标系中.
(1)求抛物线所对应的函数表达式;
(2)通过计算说明,现有一辆宽4m,高3.2m的厢式货车能否安全通过此隧道
21.(9分)如图,一次函数(,为常数,)的图象与反比例函数()的图象交于点与点
(1)求一次函数与反比例函数的解析式;
(2)根据图象直接写出当为何值时,;
(3)求出的面积.
22.(10分)如图,抛物线()经过三点;
(1)写出不等式的解集;
(2)点为第四象限内抛物线上一动点,求以四点构成的四边形面积的最大值.
23.(9分)某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元.则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润 最大的月利润是多少元
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元 根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元
参考答案
1.A
2.D
3.C
4.B
5.C
6.D
7.C
8.D
9.C
10.A
11.
12.y=-2x2+4x-1
13.-5≤y<13.
14.
15.(1);(2)不在,理由见解析
16.顶点式为,对称轴为:直线,顶点坐标为
17.(1)c<0;(2)m>n>q
18.y=(x-2)2
19.(1);(2)1或3
20.(1)y=(x-5)2+4;(2)货船能从桥下通过,理由见解析.
21.(1)y1=-2x+10,;(2)0<x<1或x>4;(3)15.
22.(1)x<-1或x>5
(2)
23.(1) y=-10x2+110x+2 100(0<x≤15且x为整数); (2) 每件55元或56元时,最大月利润为2 400元;(3)见解析.
(
2
)
(
1
)
一、选择题。(每小题只有一个正确答案,每小题3分,共30分)
1.下列函数一定是关于x的二次函数的是( )
A. B.
C. D.
2.将抛物线向上平移两个单位长度,再向右平移一个单位长度后,得到的物物线解析式是( )
A. B.
C. D.
3.抛物线与坐标轴的交点个数为( )
A.0 B.1 C.2 D.3
4.如图所示,反比例函数y=(k≠0,x>0)的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为8,则k的值为( )
A. B.2 C.2 D.2
5.若二次函数,当时,随的增大而减小,则的取值范围是( )
A. B. C. D.
6.若抛物线()恒在轴下方,则常数应满足( )
A. B.
C. D.
7.函数与的图象如图所示,有以下结论:① ② ③④当时,.其中正确的个数是( )
A.1 B.2 C.3 D.4
8.在下列函数图象上任取不同两点、,一定能使成立的是
A. B.
C. D.
9.在同一坐标系中,二次函数与一次函数的图像可能是( )
A. B.
C. D.
10.三个关于的方程:,已知常数,若、、分别是按上顺序对应三个方程的正根,则下列判断正确的是( )
A. B.
C. D.不能确定的大小
二、填空题。(每小题4分,共16分)
11.若(-2,5)、(4,5)是抛物线上的两点,则它的对称轴是_____________.
12.二次函数的图象绕其顶点旋转180°后所得图像的解析式是_____________.
13.二次函数,当时,的取值范围是_____________.
14.如图,点在双曲线上,且点A的横坐标为3,过作⊥轴,垂足为,的垂直平分线交于,则的面积为________________.
三、解答题。(共74分)
15.(8分)已知二次函数的图象经过点(0,0),且它的顶点坐标是(1,-2).
(1)求这个二次函数的表达式;
(2)判断点(3,5)是否在这个二次函数的图像上,并说明理由.
16.(6分)用配方法将二次函数转化为顶点式,并写出其对称轴和顶点坐标.
17.(8分)已知抛物线交y轴于负半轴,且与轴有两个不同的交点.
(1)求c的取值范围;
(2)若抛物线经过点、点和点,试比较的大小.
18.(8分)二次函数y=a(x-h)2的图象如图,已知a=,OA=OC,试求该抛物线的解析式.
19.(8分)如图,在平面直角坐标系中,已知点B(4,0),等腰直角三角形的直角顶点在反比例函数的图象上.
(1)求反比例函数的表达式;
(2)把向右平移个单位长度,对应得到.当这个函数图象经过一边的中点时,求的值.
20.(8分)有一个抛物线形的单向道路隧道,隧道离地面的最大高度为4m,跨度为10m,把它放在图示平面直角坐标系中.
(1)求抛物线所对应的函数表达式;
(2)通过计算说明,现有一辆宽4m,高3.2m的厢式货车能否安全通过此隧道
21.(9分)如图,一次函数(,为常数,)的图象与反比例函数()的图象交于点与点
(1)求一次函数与反比例函数的解析式;
(2)根据图象直接写出当为何值时,;
(3)求出的面积.
22.(10分)如图,抛物线()经过三点;
(1)写出不等式的解集;
(2)点为第四象限内抛物线上一动点,求以四点构成的四边形面积的最大值.
23.(9分)某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元.则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润 最大的月利润是多少元
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元 根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元
参考答案
1.A
2.D
3.C
4.B
5.C
6.D
7.C
8.D
9.C
10.A
11.
12.y=-2x2+4x-1
13.-5≤y<13.
14.
15.(1);(2)不在,理由见解析
16.顶点式为,对称轴为:直线,顶点坐标为
17.(1)c<0;(2)m>n>q
18.y=(x-2)2
19.(1);(2)1或3
20.(1)y=(x-5)2+4;(2)货船能从桥下通过,理由见解析.
21.(1)y1=-2x+10,;(2)0<x<1或x>4;(3)15.
22.(1)x<-1或x>5
(2)
23.(1) y=-10x2+110x+2 100(0<x≤15且x为整数); (2) 每件55元或56元时,最大月利润为2 400元;(3)见解析.
(
2
)
(
1
)
同课章节目录
