13.3.2等边三角形同步练习2023—2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 13.3.2等边三角形同步练习2023—2024学年人教版数学八年级上册(含答案) | 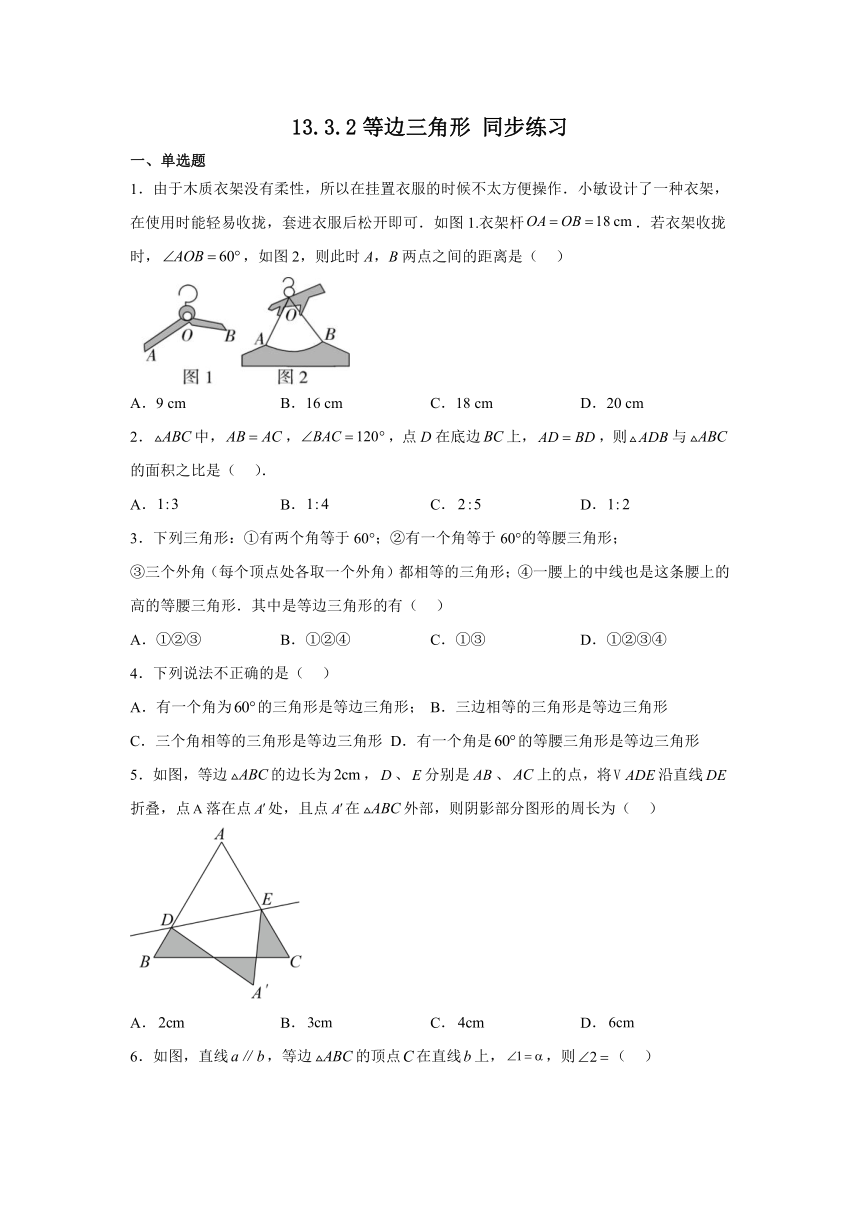 | |
| 格式 | docx | ||
| 文件大小 | 863.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 15:31:28 | ||
图片预览



文档简介
13.3.2等边三角形 同步练习
一、单选题
1.由于木质衣架没有柔性,所以在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,套进衣服后松开即可.如图1.衣架杆.若衣架收拢时,,如图2,则此时A,B两点之间的距离是( )
A.9 cm B.16 cm C.18 cm D.20 cm
2.中,,,点D在底边上,,则与的面积之比是( ).
A. B. C. D.
3.下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;
③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )
A.①②③ B.①②④ C.①③ D.①②③④
4.下列说法不正确的是( )
A.有一个角为的三角形是等边三角形; B.三边相等的三角形是等边三角形
C.三个角相等的三角形是等边三角形 D.有一个角是的等腰三角形是等边三角形
5.如图,等边的边长为,、分别是、上的点,将沿直线折叠,点落在点处,且点在外部,则阴影部分图形的周长为( )
A. B. C. D.
6.如图,直线,等边的顶点在直线上,,则( )
A. B. C. D.
7.如图,在中,,的平分线交于点,恰好是的垂直平分线,垂足为.若,则的长为( )
A.4 B.3 C.2 D.1
8.如图,是等边三角形,D为延长线上一点,,平分,下列结论:(1);(2);(3)是等边三角形;其中正确的个数为( )
A.0个 B.1个 C.2个 D.3个
二、填空题
9.如图,正三角形的三个内角平分线交于点,则 .
10.已知:在中,,则是 三角形.
11.如图,是等边三角形的角平分线,,垂足为E,边的垂直平分线交于点P,交于点F.若,则的长为 .
12.如图,是等边三角形,为角平分线,若,则的长度为 .
13.如图,在中,,,.三角尺中30°角的顶点在边上,两边分别与的边,相交于点,,连接,.
(1) ;
(2)在平移三角尺的过程中,的值 发生变化(填“会”或“不会”);当正好与平行时,的长等于 .
三、解答题
14.如图,在中,,为边的中点,于点,于点,.求证:是等边三角形.
15.如图,在中,,平分,交于点C,且,过C作交于点E,连接.
(1)求证:是等边三角形.
(2)求证:.
16.在中,为锐角,点D为射线上一点,且与点B、C不重合,连接.以为边,向外作等边三角形,连接.
(1)若,.
①如图1,当点D在线段上时,试探讨与的数量关系和此时与位置关系,并说明理由;
②如图2,当点D在线段的延长线上时,①中的结论是否仍然成立,请说明理由;
(2)如图3,若,,点D在线段上,且时,试求的度数.
17.如图,是正三角形,是等腰三角形,,,以D为顶点作一个角,角的两边分别交边于M、N两点,连接.
(1)探究之间的关系,并说明理由.
(2)若的边长为2,求的周长.
参考答案
1--8CADAD BCD
9.
10.等边
11.3
12.4
13. 不会
14.证明:∵为的中点,
∴,
∵,,
∴
在和中,
∴,
∴,
∴,
∵,
∴是等边三角形.
15.(1)证明:∵平分,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴是等边三角形;
(2)∵,
∴,
∴,
∴是等边三角形,
∴,
∵,,
∴,
∴,
∴E是的中点,
∴是边的中线,
∵是等边三角形,
∴.
16.(1)解:,;理由如下,
∵,,
∴和是等边三角形,
∴,,
∴,
在和中,
∵,,,
∴(SAS),
∴,,
∵,
∴,
∴
∴;
②成立,理由如下:
∵,
∴,即,
在和中,
∵,,,
∴(SAS),
∴,,
∵,,
∴,
∴,
∴;
(2)以点A为顶点,为边作,交BC于点E,
∴,,
∵是等边三角形,
∴,,
∴,
∵,
∴,
∵,
∴,
而,
∴,
在和中,
∵,,,
∴(AAS),
∴,
∵,
∴是等边三角形,
∴.
17.(1)解:.理由如下:
如图:延长至E,使得并连接,
∵是正三角形,是等腰三角形,
∴,
又∵,且,
∴,
∴,
∴,
在与中,,
∴,
∴,
又∵,
∴,
∴,即,
∵,
在与中,
,
∴,
∴,
又∵,
∴.
(2)解:∵为等边三角形,
∴,
利用(1)中的结论得出:,
的周长,
,
,
,
,
.
一、单选题
1.由于木质衣架没有柔性,所以在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,套进衣服后松开即可.如图1.衣架杆.若衣架收拢时,,如图2,则此时A,B两点之间的距离是( )
A.9 cm B.16 cm C.18 cm D.20 cm
2.中,,,点D在底边上,,则与的面积之比是( ).
A. B. C. D.
3.下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;
③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )
A.①②③ B.①②④ C.①③ D.①②③④
4.下列说法不正确的是( )
A.有一个角为的三角形是等边三角形; B.三边相等的三角形是等边三角形
C.三个角相等的三角形是等边三角形 D.有一个角是的等腰三角形是等边三角形
5.如图,等边的边长为,、分别是、上的点,将沿直线折叠,点落在点处,且点在外部,则阴影部分图形的周长为( )
A. B. C. D.
6.如图,直线,等边的顶点在直线上,,则( )
A. B. C. D.
7.如图,在中,,的平分线交于点,恰好是的垂直平分线,垂足为.若,则的长为( )
A.4 B.3 C.2 D.1
8.如图,是等边三角形,D为延长线上一点,,平分,下列结论:(1);(2);(3)是等边三角形;其中正确的个数为( )
A.0个 B.1个 C.2个 D.3个
二、填空题
9.如图,正三角形的三个内角平分线交于点,则 .
10.已知:在中,,则是 三角形.
11.如图,是等边三角形的角平分线,,垂足为E,边的垂直平分线交于点P,交于点F.若,则的长为 .
12.如图,是等边三角形,为角平分线,若,则的长度为 .
13.如图,在中,,,.三角尺中30°角的顶点在边上,两边分别与的边,相交于点,,连接,.
(1) ;
(2)在平移三角尺的过程中,的值 发生变化(填“会”或“不会”);当正好与平行时,的长等于 .
三、解答题
14.如图,在中,,为边的中点,于点,于点,.求证:是等边三角形.
15.如图,在中,,平分,交于点C,且,过C作交于点E,连接.
(1)求证:是等边三角形.
(2)求证:.
16.在中,为锐角,点D为射线上一点,且与点B、C不重合,连接.以为边,向外作等边三角形,连接.
(1)若,.
①如图1,当点D在线段上时,试探讨与的数量关系和此时与位置关系,并说明理由;
②如图2,当点D在线段的延长线上时,①中的结论是否仍然成立,请说明理由;
(2)如图3,若,,点D在线段上,且时,试求的度数.
17.如图,是正三角形,是等腰三角形,,,以D为顶点作一个角,角的两边分别交边于M、N两点,连接.
(1)探究之间的关系,并说明理由.
(2)若的边长为2,求的周长.
参考答案
1--8CADAD BCD
9.
10.等边
11.3
12.4
13. 不会
14.证明:∵为的中点,
∴,
∵,,
∴
在和中,
∴,
∴,
∴,
∵,
∴是等边三角形.
15.(1)证明:∵平分,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴是等边三角形;
(2)∵,
∴,
∴,
∴是等边三角形,
∴,
∵,,
∴,
∴,
∴E是的中点,
∴是边的中线,
∵是等边三角形,
∴.
16.(1)解:,;理由如下,
∵,,
∴和是等边三角形,
∴,,
∴,
在和中,
∵,,,
∴(SAS),
∴,,
∵,
∴,
∴
∴;
②成立,理由如下:
∵,
∴,即,
在和中,
∵,,,
∴(SAS),
∴,,
∵,,
∴,
∴,
∴;
(2)以点A为顶点,为边作,交BC于点E,
∴,,
∵是等边三角形,
∴,,
∴,
∵,
∴,
∵,
∴,
而,
∴,
在和中,
∵,,,
∴(AAS),
∴,
∵,
∴是等边三角形,
∴.
17.(1)解:.理由如下:
如图:延长至E,使得并连接,
∵是正三角形,是等腰三角形,
∴,
又∵,且,
∴,
∴,
∴,
在与中,,
∴,
∴,
又∵,
∴,
∴,即,
∵,
在与中,
,
∴,
∴,
又∵,
∴.
(2)解:∵为等边三角形,
∴,
利用(1)中的结论得出:,
的周长,
,
,
,
,
.
