沪科版九年级上册数学期中复习培优试卷(含解析)
文档属性
| 名称 | 沪科版九年级上册数学期中复习培优试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 373.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 16:21:10 | ||
图片预览




文档简介
沪科版九年级上册数学期中复习培优试卷
一、选择题。(每小题只有一个正确答案)
1.下列函数属于二次函数的是( )
A.y=2x﹣1 B.y= C.y=x2+2x﹣3 D.y=
2.抛物线y=(x﹣1)2+2的顶点坐标是( )
A.(1,2) B.(1,﹣2) C.(﹣1,2) D.(﹣1,﹣2)
3.设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+3上的三点,则y1,y2,y3的大小关系为( )
A.y1>y2>y3 B.y1>y3>y2 C.y3>y2>y1 D.y3>y1>y2
4. 将抛物线y=x2-2x+1向下平移2个单位,再向左平移1个单位,所得抛物线的解析式是
A.y=x2-2x-1 B.y=x2+2x-1 C.y=x2-2 D.y=x2+2
5.已知抛物线y=x2﹣x﹣1,与x轴的一个交点为(m,0),则代数式m2﹣m+2016的值为( )
A.2015 B.2016 C.2017 D.2010
6.函数y=ax﹣a与y=(a≠0)在同一直角坐标系中的图象可能是( )
A. B.
C. D.
7.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A. B. C. D.
8.如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
A.1:3 B.1:4 C.1:5 D.1:25
9.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
A. B. C. D.12
10.如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.其中正确结论是( )
A.①②③ B.①③④ C.③④⑤ D.②③⑤
二、填空题
11.若线段MN的长为1,P是MN的黄金分割点,则MP的长为__.
12.若4a﹣3b=0,则=__.
13.如果两个相似三角形周长的比是2:3,那么它们的相似比是__.
14.如图,一抛物线型拱桥,当拱顶到水面的距离为2 m时,水面宽度为4 m;那么当水位下降1m后,水面的宽度为_________m.
15.若抛物线y=x2-kx+k-1的顶点在轴上,则k=_______.
16.如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连接CD,过点B作BG丄CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF.给出以下四个结论:①; ②点F是GE的中点; ③AF=AB;④S△ABC=5S△BDF,其中正确的结论序号是__________.
三、解答题
17.已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.
18.已知二次函数y=﹣x2+2x+3
(1)在如图所示的坐标系中,画出该函数的图象
(2)根据图象回答,x取何值时,y>0?
(3)根据图象回答,x取何值时,y随x的增大而增大?x取何值时,y随x的增大而减小?
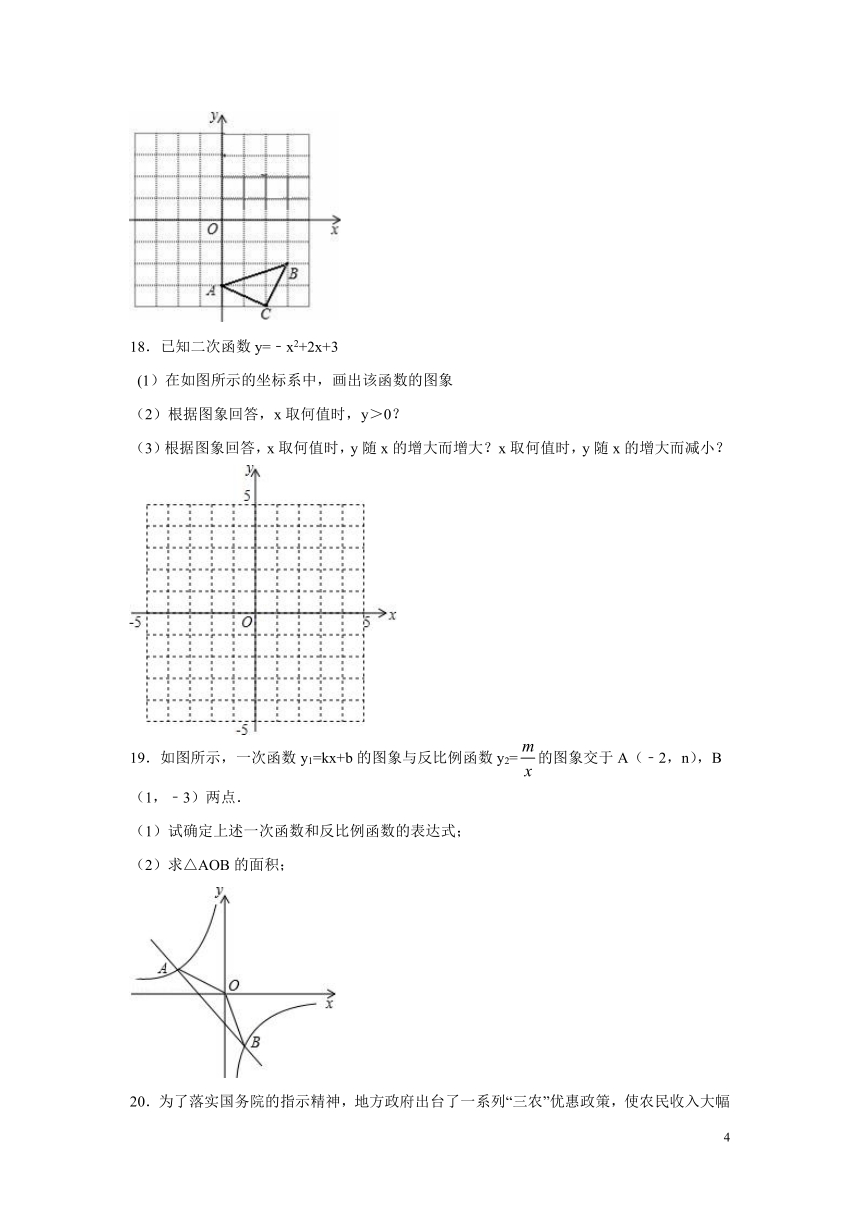
19.如图所示,一次函数y1=kx+b的图象与反比例函数y2=的图象交于A(﹣2,n),B(1,﹣3)两点.
(1)试确定上述一次函数和反比例函数的表达式;
(2)求△AOB的面积;
20.为了落实国务院的指示精神,地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:. 设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
21.在等腰△ABC中,AB=AC=10,BC=12,D为底边BC的中点,以D为顶点的角∠PDQ=∠B.
(1)如图1,若射线DQ经过点A,DP交AC边于点E,直接写出与△CDE相似的三角形;
(2)如图2,若射线DQ交AB于点F,DP交AC边于点E,设AF=x,AE为y,试写出y与x的函数关系式;(不要求写出自变量的取值范围)
(3)在(2)的条件下,连接EF,则△DEF与△CDE相似吗?试说明理由.
22.如图,在中,E是DC上一点,连接AE、F为AE上一点,且.
求证:.
23.已知:如图,△ABC中,∠BAC=90°,AB=AC,点D是BC边上的一个动点(不与B,C重合),∠ADE=45°.求证:△ABD∽△DCE.
24.2016年里约奥运会,中国女排的姑娘们在郎平教练指导下,通过刻苦训练,取得了世界冠军,为国争光,如图,已知排球场的长度OD为18米,位于球场中线处球网的高度AB为2.43米,一队员站在点O处发球,排球从点O的正上方1.8米的C点向正前方飞出,当排球运行至离点O的水平距离OE为7米时,到达最高点G建立如图所示的平面直角坐标系.
(1)当球上升的最大高度为3.2米时,求排球飞行的高度y(单位:米)与水平距离x(单位:米)的函数关系式.(不要求写自变量x的取值范围).
(2)在(1)的条件下,对方距球网0.5米的点F处有一队员,他起跳后的最大高度为3.1米,问这次她是否可以拦网成功?请通过计算说明.
(3)若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)
参考答案
1.C
【解析】
试题解析:A、y=2x-1是一次函数,故A错误;
B、y=+3自变量的次数是-2,故B错误;
C、y=x2+2x-3是二次函数,故C正确;
D、y=是反比例函数,故D错误.
故选C.
2.A
【解析】试题分析:根据抛物线的顶点式解析式写出顶点坐标即可.
解:y=(x﹣1)2+2的顶点坐标为(1,2).
故选A.
考点:二次函数的性质.
3.A
【解析】试题解析:∵函数的解析式是y=-(x+1)2+3,
∴对称轴是x=-1,
∴点A关于对称轴的点A′是(0,y1),
那么点A′、B、C都在对称轴的右边,而对称轴右边y随x的增大而减小,
于是y1>y2>y3.
故选A.
4.C
【分析】
抛物线y=x2-2x+1化为顶点坐标式再按照“左加右减,上加下减”的规律平移则可.
【详解】
解:根据题意y=x2-2x+1=(x-1)2向下平移2个单位,再向左平移1个单位,得y=(x-1+1)2-2,y=x2-2.
故选:C.
【点睛】
此题不仅考查了对平移的理解,同时考查了学生将一般式转化顶点式的能力.
5.C
【解析】
试题解析:∵抛物线y=x2-x-1与x轴的一个交点为(m,0),
∴m2-m-1=0,
∴m2-m+2016=m2-m-1+2017=2017.
故选C.
6.D
【解析】试题解析:A、从反比例函数图象得a>0,则对应的一次函数y=ax-a图象经过第一、三、四象限,所以A选项错误;
B、从反比例函数图象得a>0,则对应的一次函数y=ax-a图象经过第一、三、四象限,所以B选项错误;
C、从反比例函数图象得a<0,则对应的一次函数y=ax-a图象经过第一、二、四象限,所以C选项错误;
D、从反比例函数图象得a<0,则对应的一次函数y=ax-a图象经过第一、二、四象限,所以D选项正确.
故选D.
7.B
【详解】
根据勾股定理,AB==2,
BC==,
AC==,
所以△ABC的三边之比为:2:=1:2:,
A、三角形的三边分别为2,=,=3,三边之比为2::3=::3,故本选项错误;
B、三角形的三边分别为2,4,=2,三边之比为2:4:2=1:2:,故本选项正确;
C、三角形的三边分别为2,3,=,三边之比为2:3:,故本选项错误;
D、三角形的三边分别为=,=,4,三边之比为::4,故本选项错误.
故选B.
8.B
【详解】
∵DE∥AC,
∴△DOE∽△COA,又S△DOE:S△COA=1:25,
∴,
∵DE∥AC,
∴,
∴,
∴S△BDE与S△CDE的比是1:4,
故选B.
9.C
【解析】
试题分析:所给的三角形面积等于长方形面积减去三个直角三角形的面积,然后即可求出B的横纵坐标的积即是反比例函数的比例系数.
解:∵四边形OCBA是矩形,
∴AB=OC,OA=BC,
设B点的坐标为(a,b),
∵BD=3AD,
∴D(,b),
∵点D,E在反比例函数的图象上,
∴=k,∴E(a,),
∵S△ODE=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE=ab﹣﹣﹣ (b﹣)=9,
∴k=,
故选C.
考点:反比例函数系数k的几何意义.
10.B
【解析】试题解析:∵抛物线与x轴的一个交点在点(3,0)和(4,0)之间,而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点在点(-2,0)和(-1,0)之间.
∴当x=-1时,y>0,
即a-b+c>0,所以①正确;
∵抛物线的对称轴为直线x=-=1,即b=-2a,
∴3a+b=3a-2a=a,所以②错误;
∵抛物线的顶点坐标为(1,n),
∴=n,
∴b2=4ac-4an=4a(c-n),所以③正确;
∵抛物线与直线y=n有一个公共点,
∴抛物线与直线y=n-1有2个公共点,
∴一元二次方程ax2+bx+c=n-1有两个不相等的实数根,所以④正确.
故选B.
11.或.
【解析】
试题解析:当MP>NP时,MP=,
当MP<NP时,MP=1-=.
考点:黄金分割.
12.
【解析】
试题解析:∵4a-3b=0,
∴4a=3b,
∴.
13.2:3
【详解】
试题解析:∵两个相似三角形周长的比是2:3,
∴两个相似三角形相似比是2:3
14.2
【详解】
试题解析:如图,建立平面直角坐标系,
设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半2米,抛物线顶点C坐标为(0,2),通过以上条件可设顶点式,其中a可通过代入A点坐标(﹣2,0),到抛物线解析式得出:a=﹣0.5,所以抛物线解析式为,当水面下降1米,通过抛物线在图上的观察可转化为:
当y=﹣1时,对应的抛物线上两点之间的距离,也就是直线y=﹣1与抛物线相交的两点之间的距离,可以通过把y=﹣1代入抛物线解析式得出:,解得:x=,所以水面宽度增加到米,故答案为米.
15.k=2
【解析】
试题分析:顶点在x轴上,则说明图象与x轴只有一个交点,即-4(k-1)=0,解得:k=2.
考点:二次函数的顶点.
16.①③
【分析】
先证明△AFG∽△CFB,再根据相似三角形的性质进行判断.
【详解】
∵在Rt△ABC中,∠ABC=90°,
∴AB⊥BC,AG⊥AB,
∴AG∥BC,
∴△AFG∽△CFB,
∴,
∵BA=BC,
∴,故①正确;
∵∠ABC=90°,BG⊥CD
∴∠DBE+∠BDE=∠BDE+∠BCD=90°,
∴∠DBE=∠BCD,
∵AB=CB,点D是AB的中点,
∴BD=AB=CB,
∵tan∠BCD==,
∴在Rt△ABG中,tan∠DBE==,
∵,
∴FG=FB,故②错误;
∵△AFG∽△CFB,
∴AF:CF=AG:BC=1:2,
∴AF=AC,
∵AC=AB,
∴AF=AB,故③正确;
∵BD=AB,AF=AC,
∴S△ABC=6S△BDF,故④错误.
故答案为①③.
考点:1.相似三角形的判定与性质;2. 勾股定理;3. 等腰直角三角形.
17.(1)作图见解析;(2)作图见解析;A2坐标(﹣2,﹣2).
【解析】
试题分析(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)利用位似图形的性质得出对应点的位置进而得出.
试题解析:⑴如图所示: △A1B1C1,即为所求;⑵如图所示△A2B2C2,即为所求;A2坐标(-2,-2)
18.(1)图象见解析;(2)-1<x<3;(3)当x<1时,y随x的增大而增大.当x>1时,y随x的增大而减小.
【解析】
试题分析:(1)列表,描点,连线,画出抛物线;
(2)(3)根据图象回答问题即可.
试题解析:(1)列表:
x … -1 0 1 2 3 …
y … 0 3 4 3 0 …
描点、连线可得如图所示抛物线.
(2)当-1<x<3时,y>0;
(3)当x<1时,y随x的增大而增大.当x>1时,y随x的增大而减小.
19.(1)反比例函数的表达式为.一次函数的表达式为y=﹣x﹣1.(2).
【解析】
试题分析:(1)首先把A的坐标代入反比例函数关系式中可以求出m,再把B(1,n)代入反比例函数关系式中可以求出n的值,然后利用待定系数法就可以求出一次函数的解析式;
(2)△AOB的面积不能直接求出,要求出一次函数与x轴的交点坐标,然后利用面积的割补法球它的面积.S△AOB=S△AOC+S△BOC.
解:(1)∵点A(﹣2,1)在反比例函数的图象上,
∴m=(﹣2)×1=﹣2.
∴反比例函数的表达式为.
∵点B(1,n)也在反比例函数的图象上,
∴n=﹣2,即B(1,﹣2).
把点A(﹣2,1),点B(1,﹣2)代入一次函数y=kx+b中,
得解得.
∴一次函数的表达式为y=﹣x﹣1.
(2)∵在y=﹣x﹣1中,当y=0时,得x=﹣1.
∴直线y=﹣x﹣1与x轴的交点为C(﹣1,0).
∵线段OC将△AOB分成△AOC和△BOC,
∴S△AOB=S△AOC+S△BOC=×1×1+×1×2=+1=.
考点:一次函数综合题;反比例函数综合题.
20.(1);(2)该产品销售价定为每千克30元时,每天销售利润最大,最大销售利润200元.
【解析】
试题分析:(1)根据销售额=销售量×销售价单x,列出函数关系式;(2)用配方法将(2)的函数关系式变形,利用二次函数的性质求最大值.
试题解析:(1)由题意得:,
∴w与x的函数关系式为:.
(2),
∵﹣2<0,∴当x=30时,w有最大值.w最大值为200.
答:该产品销售价定为每千克30元时,每天销售利润最大,最大销售利润200元.
考点:1.二次函数的应用;2.由实际问题列函数关系式;3.二次函数的最值.
21.(1)(1)与△CDE相似的三角形为△ABD,△ACD,△ADE;理由见解析;(2)y=;(3)△DEF与△CDE相似.理由见解析.
【解析】
试题分析:1)由等腰三角形的性质得出∠B=∠C,∠ADB=∠ADC=90°,因此△ABD∽△ACD,证出∠PDQ=∠C,由∠DAE=∠CAD,得出△ADE∽△ACD;在证出△CDE∽△CAD,即可得出结果;
(2)证出△BDF∽△CDE,得出对应边成比例,即可得出y与x的函数关系式;
(3)由(2)可知:△BDF∽△CDE,得出证出,由∠EDF=∠C,即可得出△DEF∽△CED.
试题分析:(1)与△CDE相似的三角形为△ABD,△ACD,△ADE;理由如下:
∵AB=AC,D为底边BC的中点,
∴∠B=∠C,AD⊥BC,
∴∠ADB=∠ADC=90°,
∴△ABD∽△ACD,
∵∠PDQ=∠B,
∴∠PDQ=∠C,
又∵∠DAE=∠CAD,
∴△ADE∽△ACD;
∵∠CDE+∠PDQ=90°,
∴∠C+∠PDQ=90°,
∴∠CED=90°=∠ADC,
又∵∠C=∠C,
∴△CDE∽△CAD,
∴△△ABD∽△ACD∽△ADE∽△CDE;
(2)∵∠FDC=∠B+∠BDF,
∠FDC=∠FDE+∠EDC,
∴∠EDC=∠BDF,
∴△BDF∽△CDE,
∴,
∵D为BC的中点,
∴BD=CD=6,
∴
∴y=;
(3)△DEF与△CDE相似.理由如下:如图所示:
由(2)可知:△BDF∽△CDE,
则,
∵BD=CD,
∴,
又∵∠EDF=∠C,
∴△DEF∽△CED.
22.证明见解析.
【分析】
本题要证明,根据题目给定的条件中没有给定与边对应成比例有关的信息,只有与角有关的条件,故在方法选择上确定利用定理“两角对应相等,两三角形相似”,通过证明,即可完成.
【详解】
证明∵四边形ABCD是平行四边形,
∴,,,
∴
∵,且,
∴.
∵,
∴,
∴.
【点睛】
本题考查的是相似三角形的判定,关键是根据题意利用“两角对应相等,两三角形相似”的方法来证明两三角形相似.
23.见解析
【分析】
已知等腰直角三角形的两底角相等:∠B=∠C=45°,所以欲证明△ABD∽△DCE,只需推知∠1=∠3,由“两角法”证得结论.
【详解】
∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠2+∠ADE+∠3=180°,∠ADE=45°,
∴∠2+∠3=180°﹣∠ADE=135°,
∴∠1=∠3,
∴△ABD∽△DCE.
【点睛】
本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了等腰直角三角形的判定与性质.
24.(1)(1) (2)不能拦网成功;(3)h>
【解析】
试题分析:(1)根据题意得抛物线的顶点为(5,3),∴可以设抛物线的解析式为 ,把C(0,2)代入即可. (2)∵OD=15,∴OA=7.5, ∵对方距球网0.5米的点F,∴OF=8,把x=8代入解析式求出y的值,和2.7比较即可. (3)根据题意可以把解析式设为y=(x-5)2+h,把C(0,2)代入得
a(-5)2+h=2,,要求过网,所以当 时, ,要求不出界,所以当时, ,解不等式即可求出h的取值范围.
试题解析:
(1)
(2) 当x=8时,
不能拦网成功
(3) 设y=(x-5)2+h
将C(0,2)代入y=(x-5)2+h中,得
a(-5)2+h=2,
∴
由 解得h>
点睛:本题的难点是第3问,要把过网并且不出界的要求转化为数学问题,本题有未知数h,过网满足当,y值大于网高,不出界的转化较难,当时,,说明球不出界.
(
2
)
(
1
)
一、选择题。(每小题只有一个正确答案)
1.下列函数属于二次函数的是( )
A.y=2x﹣1 B.y= C.y=x2+2x﹣3 D.y=
2.抛物线y=(x﹣1)2+2的顶点坐标是( )
A.(1,2) B.(1,﹣2) C.(﹣1,2) D.(﹣1,﹣2)
3.设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+3上的三点,则y1,y2,y3的大小关系为( )
A.y1>y2>y3 B.y1>y3>y2 C.y3>y2>y1 D.y3>y1>y2
4. 将抛物线y=x2-2x+1向下平移2个单位,再向左平移1个单位,所得抛物线的解析式是
A.y=x2-2x-1 B.y=x2+2x-1 C.y=x2-2 D.y=x2+2
5.已知抛物线y=x2﹣x﹣1,与x轴的一个交点为(m,0),则代数式m2﹣m+2016的值为( )
A.2015 B.2016 C.2017 D.2010
6.函数y=ax﹣a与y=(a≠0)在同一直角坐标系中的图象可能是( )
A. B.
C. D.
7.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A. B. C. D.
8.如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
A.1:3 B.1:4 C.1:5 D.1:25
9.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
A. B. C. D.12
10.如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.其中正确结论是( )
A.①②③ B.①③④ C.③④⑤ D.②③⑤
二、填空题
11.若线段MN的长为1,P是MN的黄金分割点,则MP的长为__.
12.若4a﹣3b=0,则=__.
13.如果两个相似三角形周长的比是2:3,那么它们的相似比是__.
14.如图,一抛物线型拱桥,当拱顶到水面的距离为2 m时,水面宽度为4 m;那么当水位下降1m后,水面的宽度为_________m.
15.若抛物线y=x2-kx+k-1的顶点在轴上,则k=_______.
16.如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连接CD,过点B作BG丄CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF.给出以下四个结论:①; ②点F是GE的中点; ③AF=AB;④S△ABC=5S△BDF,其中正确的结论序号是__________.
三、解答题
17.已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.
18.已知二次函数y=﹣x2+2x+3
(1)在如图所示的坐标系中,画出该函数的图象
(2)根据图象回答,x取何值时,y>0?
(3)根据图象回答,x取何值时,y随x的增大而增大?x取何值时,y随x的增大而减小?
19.如图所示,一次函数y1=kx+b的图象与反比例函数y2=的图象交于A(﹣2,n),B(1,﹣3)两点.
(1)试确定上述一次函数和反比例函数的表达式;
(2)求△AOB的面积;
20.为了落实国务院的指示精神,地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:. 设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
21.在等腰△ABC中,AB=AC=10,BC=12,D为底边BC的中点,以D为顶点的角∠PDQ=∠B.
(1)如图1,若射线DQ经过点A,DP交AC边于点E,直接写出与△CDE相似的三角形;
(2)如图2,若射线DQ交AB于点F,DP交AC边于点E,设AF=x,AE为y,试写出y与x的函数关系式;(不要求写出自变量的取值范围)
(3)在(2)的条件下,连接EF,则△DEF与△CDE相似吗?试说明理由.
22.如图,在中,E是DC上一点,连接AE、F为AE上一点,且.
求证:.
23.已知:如图,△ABC中,∠BAC=90°,AB=AC,点D是BC边上的一个动点(不与B,C重合),∠ADE=45°.求证:△ABD∽△DCE.
24.2016年里约奥运会,中国女排的姑娘们在郎平教练指导下,通过刻苦训练,取得了世界冠军,为国争光,如图,已知排球场的长度OD为18米,位于球场中线处球网的高度AB为2.43米,一队员站在点O处发球,排球从点O的正上方1.8米的C点向正前方飞出,当排球运行至离点O的水平距离OE为7米时,到达最高点G建立如图所示的平面直角坐标系.
(1)当球上升的最大高度为3.2米时,求排球飞行的高度y(单位:米)与水平距离x(单位:米)的函数关系式.(不要求写自变量x的取值范围).
(2)在(1)的条件下,对方距球网0.5米的点F处有一队员,他起跳后的最大高度为3.1米,问这次她是否可以拦网成功?请通过计算说明.
(3)若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)
参考答案
1.C
【解析】
试题解析:A、y=2x-1是一次函数,故A错误;
B、y=+3自变量的次数是-2,故B错误;
C、y=x2+2x-3是二次函数,故C正确;
D、y=是反比例函数,故D错误.
故选C.
2.A
【解析】试题分析:根据抛物线的顶点式解析式写出顶点坐标即可.
解:y=(x﹣1)2+2的顶点坐标为(1,2).
故选A.
考点:二次函数的性质.
3.A
【解析】试题解析:∵函数的解析式是y=-(x+1)2+3,
∴对称轴是x=-1,
∴点A关于对称轴的点A′是(0,y1),
那么点A′、B、C都在对称轴的右边,而对称轴右边y随x的增大而减小,
于是y1>y2>y3.
故选A.
4.C
【分析】
抛物线y=x2-2x+1化为顶点坐标式再按照“左加右减,上加下减”的规律平移则可.
【详解】
解:根据题意y=x2-2x+1=(x-1)2向下平移2个单位,再向左平移1个单位,得y=(x-1+1)2-2,y=x2-2.
故选:C.
【点睛】
此题不仅考查了对平移的理解,同时考查了学生将一般式转化顶点式的能力.
5.C
【解析】
试题解析:∵抛物线y=x2-x-1与x轴的一个交点为(m,0),
∴m2-m-1=0,
∴m2-m+2016=m2-m-1+2017=2017.
故选C.
6.D
【解析】试题解析:A、从反比例函数图象得a>0,则对应的一次函数y=ax-a图象经过第一、三、四象限,所以A选项错误;
B、从反比例函数图象得a>0,则对应的一次函数y=ax-a图象经过第一、三、四象限,所以B选项错误;
C、从反比例函数图象得a<0,则对应的一次函数y=ax-a图象经过第一、二、四象限,所以C选项错误;
D、从反比例函数图象得a<0,则对应的一次函数y=ax-a图象经过第一、二、四象限,所以D选项正确.
故选D.
7.B
【详解】
根据勾股定理,AB==2,
BC==,
AC==,
所以△ABC的三边之比为:2:=1:2:,
A、三角形的三边分别为2,=,=3,三边之比为2::3=::3,故本选项错误;
B、三角形的三边分别为2,4,=2,三边之比为2:4:2=1:2:,故本选项正确;
C、三角形的三边分别为2,3,=,三边之比为2:3:,故本选项错误;
D、三角形的三边分别为=,=,4,三边之比为::4,故本选项错误.
故选B.
8.B
【详解】
∵DE∥AC,
∴△DOE∽△COA,又S△DOE:S△COA=1:25,
∴,
∵DE∥AC,
∴,
∴,
∴S△BDE与S△CDE的比是1:4,
故选B.
9.C
【解析】
试题分析:所给的三角形面积等于长方形面积减去三个直角三角形的面积,然后即可求出B的横纵坐标的积即是反比例函数的比例系数.
解:∵四边形OCBA是矩形,
∴AB=OC,OA=BC,
设B点的坐标为(a,b),
∵BD=3AD,
∴D(,b),
∵点D,E在反比例函数的图象上,
∴=k,∴E(a,),
∵S△ODE=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE=ab﹣﹣﹣ (b﹣)=9,
∴k=,
故选C.
考点:反比例函数系数k的几何意义.
10.B
【解析】试题解析:∵抛物线与x轴的一个交点在点(3,0)和(4,0)之间,而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点在点(-2,0)和(-1,0)之间.
∴当x=-1时,y>0,
即a-b+c>0,所以①正确;
∵抛物线的对称轴为直线x=-=1,即b=-2a,
∴3a+b=3a-2a=a,所以②错误;
∵抛物线的顶点坐标为(1,n),
∴=n,
∴b2=4ac-4an=4a(c-n),所以③正确;
∵抛物线与直线y=n有一个公共点,
∴抛物线与直线y=n-1有2个公共点,
∴一元二次方程ax2+bx+c=n-1有两个不相等的实数根,所以④正确.
故选B.
11.或.
【解析】
试题解析:当MP>NP时,MP=,
当MP<NP时,MP=1-=.
考点:黄金分割.
12.
【解析】
试题解析:∵4a-3b=0,
∴4a=3b,
∴.
13.2:3
【详解】
试题解析:∵两个相似三角形周长的比是2:3,
∴两个相似三角形相似比是2:3
14.2
【详解】
试题解析:如图,建立平面直角坐标系,
设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半2米,抛物线顶点C坐标为(0,2),通过以上条件可设顶点式,其中a可通过代入A点坐标(﹣2,0),到抛物线解析式得出:a=﹣0.5,所以抛物线解析式为,当水面下降1米,通过抛物线在图上的观察可转化为:
当y=﹣1时,对应的抛物线上两点之间的距离,也就是直线y=﹣1与抛物线相交的两点之间的距离,可以通过把y=﹣1代入抛物线解析式得出:,解得:x=,所以水面宽度增加到米,故答案为米.
15.k=2
【解析】
试题分析:顶点在x轴上,则说明图象与x轴只有一个交点,即-4(k-1)=0,解得:k=2.
考点:二次函数的顶点.
16.①③
【分析】
先证明△AFG∽△CFB,再根据相似三角形的性质进行判断.
【详解】
∵在Rt△ABC中,∠ABC=90°,
∴AB⊥BC,AG⊥AB,
∴AG∥BC,
∴△AFG∽△CFB,
∴,
∵BA=BC,
∴,故①正确;
∵∠ABC=90°,BG⊥CD
∴∠DBE+∠BDE=∠BDE+∠BCD=90°,
∴∠DBE=∠BCD,
∵AB=CB,点D是AB的中点,
∴BD=AB=CB,
∵tan∠BCD==,
∴在Rt△ABG中,tan∠DBE==,
∵,
∴FG=FB,故②错误;
∵△AFG∽△CFB,
∴AF:CF=AG:BC=1:2,
∴AF=AC,
∵AC=AB,
∴AF=AB,故③正确;
∵BD=AB,AF=AC,
∴S△ABC=6S△BDF,故④错误.
故答案为①③.
考点:1.相似三角形的判定与性质;2. 勾股定理;3. 等腰直角三角形.
17.(1)作图见解析;(2)作图见解析;A2坐标(﹣2,﹣2).
【解析】
试题分析(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)利用位似图形的性质得出对应点的位置进而得出.
试题解析:⑴如图所示: △A1B1C1,即为所求;⑵如图所示△A2B2C2,即为所求;A2坐标(-2,-2)
18.(1)图象见解析;(2)-1<x<3;(3)当x<1时,y随x的增大而增大.当x>1时,y随x的增大而减小.
【解析】
试题分析:(1)列表,描点,连线,画出抛物线;
(2)(3)根据图象回答问题即可.
试题解析:(1)列表:
x … -1 0 1 2 3 …
y … 0 3 4 3 0 …
描点、连线可得如图所示抛物线.
(2)当-1<x<3时,y>0;
(3)当x<1时,y随x的增大而增大.当x>1时,y随x的增大而减小.
19.(1)反比例函数的表达式为.一次函数的表达式为y=﹣x﹣1.(2).
【解析】
试题分析:(1)首先把A的坐标代入反比例函数关系式中可以求出m,再把B(1,n)代入反比例函数关系式中可以求出n的值,然后利用待定系数法就可以求出一次函数的解析式;
(2)△AOB的面积不能直接求出,要求出一次函数与x轴的交点坐标,然后利用面积的割补法球它的面积.S△AOB=S△AOC+S△BOC.
解:(1)∵点A(﹣2,1)在反比例函数的图象上,
∴m=(﹣2)×1=﹣2.
∴反比例函数的表达式为.
∵点B(1,n)也在反比例函数的图象上,
∴n=﹣2,即B(1,﹣2).
把点A(﹣2,1),点B(1,﹣2)代入一次函数y=kx+b中,
得解得.
∴一次函数的表达式为y=﹣x﹣1.
(2)∵在y=﹣x﹣1中,当y=0时,得x=﹣1.
∴直线y=﹣x﹣1与x轴的交点为C(﹣1,0).
∵线段OC将△AOB分成△AOC和△BOC,
∴S△AOB=S△AOC+S△BOC=×1×1+×1×2=+1=.
考点:一次函数综合题;反比例函数综合题.
20.(1);(2)该产品销售价定为每千克30元时,每天销售利润最大,最大销售利润200元.
【解析】
试题分析:(1)根据销售额=销售量×销售价单x,列出函数关系式;(2)用配方法将(2)的函数关系式变形,利用二次函数的性质求最大值.
试题解析:(1)由题意得:,
∴w与x的函数关系式为:.
(2),
∵﹣2<0,∴当x=30时,w有最大值.w最大值为200.
答:该产品销售价定为每千克30元时,每天销售利润最大,最大销售利润200元.
考点:1.二次函数的应用;2.由实际问题列函数关系式;3.二次函数的最值.
21.(1)(1)与△CDE相似的三角形为△ABD,△ACD,△ADE;理由见解析;(2)y=;(3)△DEF与△CDE相似.理由见解析.
【解析】
试题分析:1)由等腰三角形的性质得出∠B=∠C,∠ADB=∠ADC=90°,因此△ABD∽△ACD,证出∠PDQ=∠C,由∠DAE=∠CAD,得出△ADE∽△ACD;在证出△CDE∽△CAD,即可得出结果;
(2)证出△BDF∽△CDE,得出对应边成比例,即可得出y与x的函数关系式;
(3)由(2)可知:△BDF∽△CDE,得出证出,由∠EDF=∠C,即可得出△DEF∽△CED.
试题分析:(1)与△CDE相似的三角形为△ABD,△ACD,△ADE;理由如下:
∵AB=AC,D为底边BC的中点,
∴∠B=∠C,AD⊥BC,
∴∠ADB=∠ADC=90°,
∴△ABD∽△ACD,
∵∠PDQ=∠B,
∴∠PDQ=∠C,
又∵∠DAE=∠CAD,
∴△ADE∽△ACD;
∵∠CDE+∠PDQ=90°,
∴∠C+∠PDQ=90°,
∴∠CED=90°=∠ADC,
又∵∠C=∠C,
∴△CDE∽△CAD,
∴△△ABD∽△ACD∽△ADE∽△CDE;
(2)∵∠FDC=∠B+∠BDF,
∠FDC=∠FDE+∠EDC,
∴∠EDC=∠BDF,
∴△BDF∽△CDE,
∴,
∵D为BC的中点,
∴BD=CD=6,
∴
∴y=;
(3)△DEF与△CDE相似.理由如下:如图所示:
由(2)可知:△BDF∽△CDE,
则,
∵BD=CD,
∴,
又∵∠EDF=∠C,
∴△DEF∽△CED.
22.证明见解析.
【分析】
本题要证明,根据题目给定的条件中没有给定与边对应成比例有关的信息,只有与角有关的条件,故在方法选择上确定利用定理“两角对应相等,两三角形相似”,通过证明,即可完成.
【详解】
证明∵四边形ABCD是平行四边形,
∴,,,
∴
∵,且,
∴.
∵,
∴,
∴.
【点睛】
本题考查的是相似三角形的判定,关键是根据题意利用“两角对应相等,两三角形相似”的方法来证明两三角形相似.
23.见解析
【分析】
已知等腰直角三角形的两底角相等:∠B=∠C=45°,所以欲证明△ABD∽△DCE,只需推知∠1=∠3,由“两角法”证得结论.
【详解】
∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠2+∠ADE+∠3=180°,∠ADE=45°,
∴∠2+∠3=180°﹣∠ADE=135°,
∴∠1=∠3,
∴△ABD∽△DCE.
【点睛】
本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了等腰直角三角形的判定与性质.
24.(1)(1) (2)不能拦网成功;(3)h>
【解析】
试题分析:(1)根据题意得抛物线的顶点为(5,3),∴可以设抛物线的解析式为 ,把C(0,2)代入即可. (2)∵OD=15,∴OA=7.5, ∵对方距球网0.5米的点F,∴OF=8,把x=8代入解析式求出y的值,和2.7比较即可. (3)根据题意可以把解析式设为y=(x-5)2+h,把C(0,2)代入得
a(-5)2+h=2,,要求过网,所以当 时, ,要求不出界,所以当时, ,解不等式即可求出h的取值范围.
试题解析:
(1)
(2) 当x=8时,
不能拦网成功
(3) 设y=(x-5)2+h
将C(0,2)代入y=(x-5)2+h中,得
a(-5)2+h=2,
∴
由 解得h>
点睛:本题的难点是第3问,要把过网并且不出界的要求转化为数学问题,本题有未知数h,过网满足当,y值大于网高,不出界的转化较难,当时,,说明球不出界.
(
2
)
(
1
)
同课章节目录
