沪科版九年级上册数学期中复习培优试卷(含解析)
文档属性
| 名称 | 沪科版九年级上册数学期中复习培优试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 500.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 00:00:00 | ||
图片预览




文档简介
沪科版九年级上册数学期中复习培优试题
一、选择题。(每小题只有一个正确答案)
1.抛物线y=2(x-3)2+4的顶点坐标是( )
A.(3,4) B.(-3,4) C.(3,-4) D.(2,4)
2.已知2x=3y,则下列比例式成立的是( )
A. B. C. D.
3.将抛物线向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数表达式为( )
A. B. C. D.
4.二次函数的图象与轴( )
A.有两个交点,且它们位于轴同侧 B.只有一个交点
C.有两个交点,且它们位于轴两侧 D.无交点
5.如图,△ABC中,AD、BE是两条中线,则S△EDC:S△ABC=( )
A.1:2 B.2:3 C.1:3 D.1:4
6.下表是一组二次函数的自变量x与函数值y的对应值:
x 1 1.1 1.2 1.3 1.4
y -1 -0.49 0.04 0.59 1.16
那么方程的一个近似根是( )
A.1 B.1.1 C.1.2 D.1.3
7.如图,直线与轴交于点A,与双曲线交于点B,若,则的值是( )
A.4 B.3 C.2 D.1
8.如图,已知正方形ABCD的边长为4,P是BC边上一动点(与B,C不重合)连接AP,作PE⊥AP交∠BCD的外角平分线于E,设BP=,△PCE的面积为,则与的函数关系式是( )
A. B. C. D.
9.如图,在正方形ABCD中,点E、F分别在边BC,DC上,AE、AF分别交BD于点M、N,连接CN、EN,且CN=EN.下列结论:①AN=EN,AN⊥EN;②BE+DF=EF;③∠DFE=2∠AMN;④;④图中有4对相似三角形.其中正确结论个数是( )
A.5 B.4 C.3 D.2
10.如图,反比例函数的图象经过矩形OABC的边AB的中点D ,则矩形OABC的面积为( )
A.2 B.4 C.5 D.8
二、填空题
11.抛物线经过点A(-3,0),B(1,0),则抛物线的对称轴是__________.
12.如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为___米.
13.二次函数的图象如图,若一元二次方程有实数根,则 的最大值为___
14.如图,将一张直角三角形纸片BEC的斜边放在矩形ABCD的BC边上,恰好完全重合,BE、CE分别交AD于点F、G,BC=6,AF:FG:GD=3:2:1,则AB的长为________.
15.若,则_______.
三、解答题
16.以A(-1,4)为顶点的二次函数的图象经过点B(2,-5),求该函数的表达式.
17.在△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D
(1)求证:; (2)求线段AD的长.
18.已知函数(m为常数).
(1)求证:不论m为何值,该函数图象的顶点都在函数的图象上.
(2)当﹣2≤m≤3时,求该函数的图象的顶点纵坐标的取值范围.
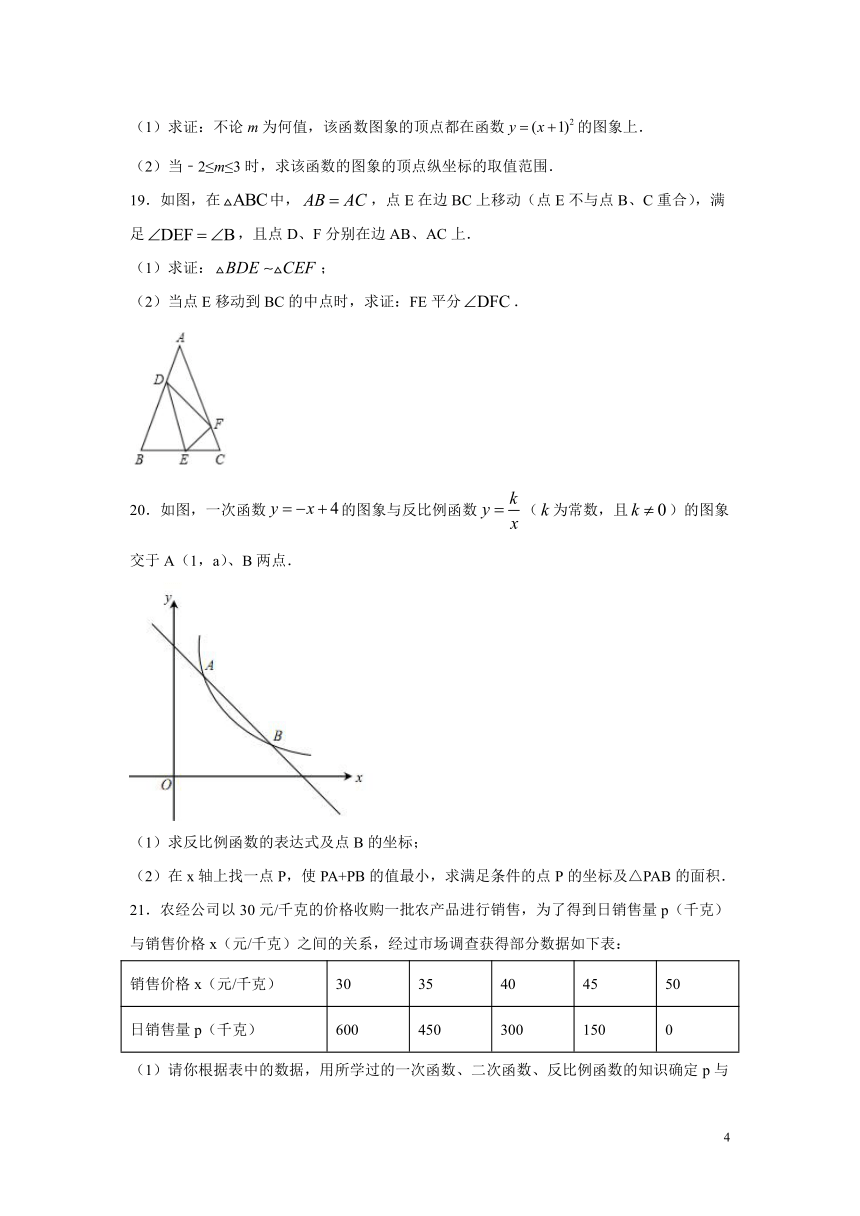
19.如图,在中,,点E在边BC上移动(点E不与点B、C重合),满足,且点D、F分别在边AB、AC上.
(1)求证:;
(2)当点E移动到BC的中点时,求证:FE平分.
20.如图,一次函数的图象与反比例函数(为常数,且)的图象交于A(1,a)、B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
21.农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) 30 35 40 45 50
日销售量p(千克) 600 450 300 150 0
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)
22.如图,是的高,点、分别在、上,且,交于点.设,,,.
(1)求的长;
(2)求点到的距离.
23.如图, 已知△ADE∽△ABC,且AD=6,AE=4,AB=12,求CD的长.
24.如图,一次函数y1=k1x+b的图象与反比例函数y2=的图象相交于A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,-4),连接AO,AO=5,sin∠AOC=.
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积;
(3)请直接写出当x<m时,y2的取值范围.
参考答案
1.A
【详解】
根据 的顶点坐标为 ,易得抛物线y=2(x﹣3)2+4顶点坐标是(3,4).故选A.
2.C
【分析】
把各个选项依据比例的基本性质,两内项之积等于两外项之积,已知的比例式可以转化为等积式2x=3y,即可判断
【详解】
解:A、变成等积式是:xy=6,故错误;
B、变成等积式是:3x=2y,故错误;
C、变成等积式是:2x=3y,故正确;
D、变成等积式是:3x=2y,故错误.
故选:C.
【点睛】
本题主要考查了判断两个比例式是否能够互化的方法,即转化为等积式,判断是否相同即可.
3.A
【分析】
先确定抛物线y=x2的顶点坐标为(0,0),再根据点平移的规律得到点(0,0)平移后所得对应点的坐标为(-2,-3),然后根据顶点式写出平移后的抛物线解析式.
【详解】
抛物线y=x2的顶点坐标为(0,0),把点(0,0)向左平移1个单位,再向下平移2个单位长度所得对应点的坐标为(-2,-3),所以平移后的抛物线解析式为y=(x+2)2-3.
故选A.
4.C
【解析】
令y=0,求二次函数与x轴的交点,可得:,解得:
所以二次函数与x轴的交点坐标为:(-1,0),(3,0),故选C.
5.D
【详解】
试题分析:∵△ABC中,AD、BE是两条中线,
∴DE是△ABC的中位线,
∴DE∥AB,DE=AB,
∴△EDC∽△ABC,
∴S△EDC:S△ABC=()2=.
故选D.
考点:1.相似三角形的判定与性质;2.三角形中位线定理.
6.C
【详解】
解:观察表格得:方程x2+3x﹣5=0的一个近似根为1.2,
故选C
考点:图象法求一元二次方程的近似根.
7.D
【解析】
因为直线与轴交于点A,所以令y=0,可得:,解得,
则OA=2b,又因为,所以B点纵坐标是:,因为B点在,所以B点坐标为(-2b,),又因为B点在直线上,所以,解得,因为直线与轴交于正半轴,所以,所以,故选D.
8.C
【解析】
过点E作EH⊥BC的延长线于点H,因为∠APB+∠EPC=90°, ∠BAP+∠APB=90°,
所以∠BAP=∠EPH,因为∠B=∠H,所以△ABP∽△PHE,设EH=a,因为∠ECH=45°, ∠H=90°,所以CH=EH=a,因为BP=x,所以CP=4-x,根据相似三角形的性质,可知,即
,整理得:,解得,所以y与x的函数关系式为:,故选C.
9.B
【详解】
将△ABE绕点A逆时针旋转90°,得到△ADH,
因为四边形ABCD是正方形,
所以AB=BC=AD, ∠BAD=∠ABC=90°,∠ABD=∠CBD=45°,
在△BNA和△BNC中,
,
所以△BNA≌△BNC,
所以AN=CN,
∠NEC=∠NCE=∠BAN,
因为∠NEC+∠BEN=180°,
所以∠BAN+∠BEN=180°,
所以∠ABC+∠ANE=180°,
所以∠ANE=90°,
所以AN=NE,AN⊥NE,故①正确,
因为∠3=45°, ∠1=∠4,
所以∠2+∠4=∠2+∠1=45°,
所以∠3=∠FAH=45°,
因为AF=AF,AE=AH,
所以△AFE≌△AFH,
所以EF=FH=DF+DH=DF+BE, ∠AFH=∠AFE,故②正确,
因为∠MAN=∠NDF=45°, ∠ANM=∠NDF,
所以∠AMN=∠AFD,
又因为∠AFE=∠AFD, ∠DFE=∠AFE+∠AFD
所以∠DFE=2∠AMN,故③正确,
因为∠MAN=∠EAF, ∠AMN=∠AFE,
所以△AMN∽△AFE,
所以,
所以MN,
如图2中,将△ABN绕点A逆时针旋转90°,得到△ADG,
易证△ANG≌△ANM, △GDN是直角三角形,
所以MN=GN,
所以,
所以,故④正确,
图中相似三角形有△ANE∽△BAD∽△BCD, △ANM∽△AEF, △ABN∽△FDN,
△BEM∽△DAM等,故⑤错误,故选B.
10.B
【解析】
试题分析:∵,∴OA OD=2.∵D是AB的中点,∴AB=2AD,∴矩形的面积=OA AB=2AD OA=2×2=4.故选B.
考点:反比例函数系数k的几何意义.
11.
【解析】
因为二次函数与x轴的交点是关于对称轴对称的两点,根据对称性可得:抛物线的对称轴,故答案为:.
12.5
【详解】
根据题意,易得△MBA∽△MCO,
根据相似三角形的性质可知,即,解得AM=5.
∴小明的影长为5米.
13.3
【详解】
试题解析::∵抛物线的开口向上,顶点纵坐标为-3,
∴a>0.
-=-3,即b2=12a,
∵一元二次方程ax2+bx+m=0有实数根,
∴△=b2-4am≥0,即12a-4am≥0,即12-4m≥0,解得m≤3,
∴m的最大值为3,
14.
【解析】
因为BC=6,AF:FG:GD=3:2:1,所以AF=3,DG=1,
因为∠AFB=∠GFE,∠A=∠E=90°,
所以∠ABF=∠FGE,
又因为∠FGE=∠DGC,
所以∠ABF=∠DGC,
因为∠A=∠D=90°,
所以△AFB∽△DCG,
所以,
因为AB=CD,
所以即,
所以,
所以.
故答案为:.
15.或
【分析】
用含k的式子分别表示出,,,然后相加整理得到一个等式,对等式进行分析可得到k的值.
【详解】
解:,
,,
,
,
或,
当时,,
当时,,
所以,或.
故答案为:或.
【点睛】
本题考查了分式的化简求值,解题关键在于将式子变形为.
16.
【解析】
试题分析:根据已知条件二次函数的顶点坐标A(-1,4)可设二次函数顶点式即:
,然后根据二次函数经过点B(2, -5),代入可求得a=,然后代入解析式即可求解.
试题解析:由顶点A(-1,4),可设函数解析式为,
∵二次函数的图象过点B(2,-5),
∴,
解得,
∴二次函数解析式为.
17.(1)见解析;(2).
【解析】
试题分析:(1)先根据AB=AC,可证得△ABC是等腰三角形,由∠A=36°,可得∠ABC=∠C=72°,因为BD平分∠ABC交AC于点D,所以∠CBD=∠ABD=36°,
∠BDC=∠C =72°,根据等角对等边可得: AD=BD=BC, 根据∠CBD=∠A,∠C=∠C,
可判定△CBD∽△CAB,根据相似三角形对应边成比例可得:,即可求证
,(2)设AD=x,则CD=1-x,再根据,可得,
解得:.
试题解析:(1)∵AB=AC=1,∠A=36°,
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠CBD=∠ABD=36°,∠BDC=72°,
∴AD=BD=BC,
∵∠CBD=∠A,∠C=∠C,
∴△CBD∽△CAB,
∴,即
(2)由(1)得,点D是AC的一个黄金分割点,
∴AD=.
18.(1)见解析;(2)0≤z≤4.
【解析】
试题分析:先根据顶点坐标公式计算出函数(m为常数)的顶点坐标,然后把顶点坐标横坐标代入的图象上可求出对应的函数值,函数值与顶点坐标的纵坐标相等,即可证明,(2)把顶点纵坐标看成关于m的二次函数,然后根据二次函数图象性质,在﹣2≤m≤3范围内求出顶点坐标纵坐标的最大值和最小值,即可求解.
试题解析:∵的顶点坐标为 ,
把代入得:,
∴不论m为何值,该函数的图象的顶点都在函数的图象上,
(2)设函数,
当时,有最小值为0,
当时,随m的增大而减小,当m>﹣1时,z随m的增大而增大,
当m=﹣2时,z=,当m=3时,z=4,
∴当﹣2≤m≤3时,该函数图象的顶点纵坐标的取值范围是0≤z≤4.
19.(1)证明见解析;(2)证明见解析
【分析】
(1)根据等腰三角形的性质可得∠B=∠C,再由∠DEF+∠CEF=∠B+∠BDE,,即可判定,根据相似三角形的判定方法即可得△BDE∽△CEF;(2)由相似三角形的性质可得,再由点E是BC的中点,可得BE=CE,即可得,又因,即可判定△CEF∽△EDF,根据相似三角形的性质可得,即可证得即FE平分∠DFC.
【详解】
解:(1)因为AB=AC,所以∠B=∠C,
因为∠DEF+∠CEF=∠B+∠BDE,
所以,
所以△BDE∽△CEF;
(2)因为△BDE∽△CEF,所以,
因为点E是BC的中点,所以BE=CE,即,
所以,又,故△CEF∽△EDF,
所以,即FE平分∠DFC.
20.(1),;(2)P ,.
【详解】
试题分析:(1)由点A在一次函数图象上,结合一次函数解析式可求出点A的坐标,再由点A的坐标利用待定系数法即可求出反比例函数解析式,联立两函数解析式成方程组,解方程组即可求出点B坐标;
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,连接PB.由点B、D的对称性结合点B的坐标找出点D的坐标,设直线AD的解析式为y=mx+n,结合点A、D的坐标利用待定系数法求出直线AD的解析式,令直线AD的解析式中y=0求出点P的坐标,再通过分割图形结合三角形的面积公式即可得出结论.
试题解析:(1)把点A(1,a)代入一次函数y=-x+4,
得:a=-1+4,解得:a=3,
∴点A的坐标为(1,3).
把点A(1,3)代入反比例函数y=,
得:3=k,
∴反比例函数的表达式y=,
联立两个函数关系式成方程组得:,
解得:,或,
∴点B的坐标为(3,1).
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,连接PB,如图所示.
∵点B、D关于x轴对称,点B的坐标为(3,1),
∴点D的坐标为(3,- 1).
设直线AD的解析式为y=mx+n,
把A,D两点代入得:,
解得:,
∴直线AD的解析式为y=-2x+5.
令y=-2x+5中y=0,则-2x+5=0,
解得:x=,
∴点P的坐标为(,0).
S△PAB=S△ABD-S△PBD=BD (xB-xA)-BD (xB-xP)
=×[1-(-1)]×(3-1)-×[1-(-1)]×(3-)
=.
考点:1.反比例函数与一次函数的交点问题;2.待定系数法求一次函数解析式;3.轴对称-最短路线问题.
21.(1)函数关系为p=﹣30x+1500;(2)这批农产品的销售价格定为40元,才能使日销售利润最大;(3)a的值为2.
【分析】
(1)首先根据表中的数据,可猜想y与x是一次函数关系,任选两点求表达式,再验证猜想的正确性;
(2)根据题意列出日销售利润w与销售价格x之间的函数关系式,根据二次函数的性质确定最大值即可;
(3)根据题意列出日销售利润w与销售价格x之间的函数关系式,并求得抛物线的对称轴,再分两种情况进行讨论,依据二次函数的性质求得a的值.
【详解】
(1)假设p与x成一次函数关系,设函数关系式为p=kx+b,
则,
解得:k=﹣30,b=1500,
∴p=﹣30x+1500,
检验:当x=35,p=450;当x=45,p=150;当x=50,p=0,符合一次函数解析式,
∴所求的函数关系为p=﹣30x+1500;
(2)设日销售利润w=p(x﹣30)=(﹣30x+1500)(x﹣30)
即w=﹣30x2+2400x﹣45000,
∴当x=﹣=40时,w有最大值3000元,
故这批农产品的销售价格定为40元,才能使日销售利润最大;
(3)日获利w=p(x﹣30﹣a)=(﹣30x+1500)(x﹣30﹣a),
即w=﹣30x2+(2400+30a)x﹣(1500a+45000),
对称轴为x=﹣=40+a,
①若a≥10,则当x=45时,w有最大值,
即w=2250﹣150a<2430(不合题意);
②若a<10,则当x=40+a时,w有最大值,
将x=40+a代入,可得w=30(a2﹣10a+100),
当w=2430时,2430=30(a2﹣10a+100),
解得a1=2,a2=-38(舍去),
综上所述,a的值为2.
【点睛】
本题主要考查二次函数的应用,解题的关键是:
(1) 首先根据表中的数据,可猜想y与x是一次函数关系, 任选两点求表达式,再验证猜想的正确性;
(2)根据题意列出日销售利润w与销售价格x之间的函数关系式,根据二次函数的性质确定最大值即可;
(3)根据题意列出日销售利润w与销售价格x之间的函数关系式,并求得抛物线的对称轴,再分两种情况进行讨论,依据二次函数的性质求得a的值.
22.(1)8 (2)6
【分析】
(1)由DE∥BC,得到△ADE∽△ABC,根据相似三角形的性质得到,代入数据即可得到结论;
(2)根据平行线的性质得到AF⊥DE,根据DE∥BC,推出△ADG∽△ABF,根据相似三角形的性质得到,代入数据即可得到结论.
【详解】
解:(1)∵,
∴∽,
∴,
∵,,,
∴,
∴;
(2)∵是的高,
∴,
∵,
∴,
∵,
∴∽,
∴,
∵,
∴,
∴,
即点到的距离是6.
【点睛】
本题考查了相似三角形的判定和性质,平行线的性质,熟练掌握相似三角形的判定和性质是解题的关键.
23.CD=2.
【分析】
根据三角形相似的性质求解即可.
【详解】
∵△ADE∽△ABC,
∴.
∵AD=6,AE=4,AB=12,
∴.
∴AC=8.
∴CD=AC-AD=8-6=2.
【点睛】
本题考查的是相似三角形的性质,熟知相似三角形的对应边成比例是解答此题的关键.
24.(1)y2=-;(2)S△AOB=;(3)当x<3时,y2>0或y2<-4.
【解析】
【分析】
(1)过点A作AE⊥轴于点E,在Rt△AEO中,通过解直角三角形可求出点A的坐标,由反比例函数图象上点的坐标特征即可求出反比例函数的解析式;
(2)由反比例函数图象上点的坐标特征可求出点B的坐标,根据点A、B的坐标,利用待定系数法可求出直线AB的解析式,再根据一次函数图象上点的坐标特征可求出点C的坐标,利用三角形的面积公式即可求出△AOB的面积;
(3)观察函数图象可得出:<0以及0<<3时,的取值范围,合在一起即可得出结论.
【详解】
解:(1)过点A作AE⊥x轴于点E,如图所示.
在Rt△AEO中,AO=5,sin∠AOC=,
∴AE=AO sin∠AOC=5×=3,
∴OE==4,
∴点A的坐标为(-4,3).
∵点A在反比例函数y2=的图象上,
∴k2=-4×3=-12,
∴反比例函数的解析式为y2=-.
(2)∵点B(m,-4)反比例函数y2=-的图象上,
∴-4=-,解得:m=3,
∴点B的坐标为(3,-4).
将A(-4,3)、B(3,-4)代入y1=k1x+b中,
,解得:,
∴直线AB的解析式为y=-x-1.
当y=-x-1=0时,x=-1,
∴点C的坐标为(-1,0),
∴S△AOB=OC (yA-yB)=×1×[3-(-4)]=.
(3)观察函数图象可知:当x<0时,y2>0;当0<x<3时,y2<-4.
∴当x<3时,y2>0或y2<-4.
【点睛】
本题考查了反比例函数与一次函数的交点问题、待定系数法求一次函数解析式、反比例(一次)函数图象上点的坐标特征以及三角形的面积,解题的关键是:(1)通过解直角三角形找出点A的坐标;(2)根据点A、B的坐标,利用待定系数法求出直线AB的解析式;(3)观察函数图象,找出当<m时,的取值范围.
(
2
)
(
1
)
一、选择题。(每小题只有一个正确答案)
1.抛物线y=2(x-3)2+4的顶点坐标是( )
A.(3,4) B.(-3,4) C.(3,-4) D.(2,4)
2.已知2x=3y,则下列比例式成立的是( )
A. B. C. D.
3.将抛物线向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数表达式为( )
A. B. C. D.
4.二次函数的图象与轴( )
A.有两个交点,且它们位于轴同侧 B.只有一个交点
C.有两个交点,且它们位于轴两侧 D.无交点
5.如图,△ABC中,AD、BE是两条中线,则S△EDC:S△ABC=( )
A.1:2 B.2:3 C.1:3 D.1:4
6.下表是一组二次函数的自变量x与函数值y的对应值:
x 1 1.1 1.2 1.3 1.4
y -1 -0.49 0.04 0.59 1.16
那么方程的一个近似根是( )
A.1 B.1.1 C.1.2 D.1.3
7.如图,直线与轴交于点A,与双曲线交于点B,若,则的值是( )
A.4 B.3 C.2 D.1
8.如图,已知正方形ABCD的边长为4,P是BC边上一动点(与B,C不重合)连接AP,作PE⊥AP交∠BCD的外角平分线于E,设BP=,△PCE的面积为,则与的函数关系式是( )
A. B. C. D.
9.如图,在正方形ABCD中,点E、F分别在边BC,DC上,AE、AF分别交BD于点M、N,连接CN、EN,且CN=EN.下列结论:①AN=EN,AN⊥EN;②BE+DF=EF;③∠DFE=2∠AMN;④;④图中有4对相似三角形.其中正确结论个数是( )
A.5 B.4 C.3 D.2
10.如图,反比例函数的图象经过矩形OABC的边AB的中点D ,则矩形OABC的面积为( )
A.2 B.4 C.5 D.8
二、填空题
11.抛物线经过点A(-3,0),B(1,0),则抛物线的对称轴是__________.
12.如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为___米.
13.二次函数的图象如图,若一元二次方程有实数根,则 的最大值为___
14.如图,将一张直角三角形纸片BEC的斜边放在矩形ABCD的BC边上,恰好完全重合,BE、CE分别交AD于点F、G,BC=6,AF:FG:GD=3:2:1,则AB的长为________.
15.若,则_______.
三、解答题
16.以A(-1,4)为顶点的二次函数的图象经过点B(2,-5),求该函数的表达式.
17.在△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D
(1)求证:; (2)求线段AD的长.
18.已知函数(m为常数).
(1)求证:不论m为何值,该函数图象的顶点都在函数的图象上.
(2)当﹣2≤m≤3时,求该函数的图象的顶点纵坐标的取值范围.
19.如图,在中,,点E在边BC上移动(点E不与点B、C重合),满足,且点D、F分别在边AB、AC上.
(1)求证:;
(2)当点E移动到BC的中点时,求证:FE平分.
20.如图,一次函数的图象与反比例函数(为常数,且)的图象交于A(1,a)、B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
21.农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) 30 35 40 45 50
日销售量p(千克) 600 450 300 150 0
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)
22.如图,是的高,点、分别在、上,且,交于点.设,,,.
(1)求的长;
(2)求点到的距离.
23.如图, 已知△ADE∽△ABC,且AD=6,AE=4,AB=12,求CD的长.
24.如图,一次函数y1=k1x+b的图象与反比例函数y2=的图象相交于A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,-4),连接AO,AO=5,sin∠AOC=.
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积;
(3)请直接写出当x<m时,y2的取值范围.
参考答案
1.A
【详解】
根据 的顶点坐标为 ,易得抛物线y=2(x﹣3)2+4顶点坐标是(3,4).故选A.
2.C
【分析】
把各个选项依据比例的基本性质,两内项之积等于两外项之积,已知的比例式可以转化为等积式2x=3y,即可判断
【详解】
解:A、变成等积式是:xy=6,故错误;
B、变成等积式是:3x=2y,故错误;
C、变成等积式是:2x=3y,故正确;
D、变成等积式是:3x=2y,故错误.
故选:C.
【点睛】
本题主要考查了判断两个比例式是否能够互化的方法,即转化为等积式,判断是否相同即可.
3.A
【分析】
先确定抛物线y=x2的顶点坐标为(0,0),再根据点平移的规律得到点(0,0)平移后所得对应点的坐标为(-2,-3),然后根据顶点式写出平移后的抛物线解析式.
【详解】
抛物线y=x2的顶点坐标为(0,0),把点(0,0)向左平移1个单位,再向下平移2个单位长度所得对应点的坐标为(-2,-3),所以平移后的抛物线解析式为y=(x+2)2-3.
故选A.
4.C
【解析】
令y=0,求二次函数与x轴的交点,可得:,解得:
所以二次函数与x轴的交点坐标为:(-1,0),(3,0),故选C.
5.D
【详解】
试题分析:∵△ABC中,AD、BE是两条中线,
∴DE是△ABC的中位线,
∴DE∥AB,DE=AB,
∴△EDC∽△ABC,
∴S△EDC:S△ABC=()2=.
故选D.
考点:1.相似三角形的判定与性质;2.三角形中位线定理.
6.C
【详解】
解:观察表格得:方程x2+3x﹣5=0的一个近似根为1.2,
故选C
考点:图象法求一元二次方程的近似根.
7.D
【解析】
因为直线与轴交于点A,所以令y=0,可得:,解得,
则OA=2b,又因为,所以B点纵坐标是:,因为B点在,所以B点坐标为(-2b,),又因为B点在直线上,所以,解得,因为直线与轴交于正半轴,所以,所以,故选D.
8.C
【解析】
过点E作EH⊥BC的延长线于点H,因为∠APB+∠EPC=90°, ∠BAP+∠APB=90°,
所以∠BAP=∠EPH,因为∠B=∠H,所以△ABP∽△PHE,设EH=a,因为∠ECH=45°, ∠H=90°,所以CH=EH=a,因为BP=x,所以CP=4-x,根据相似三角形的性质,可知,即
,整理得:,解得,所以y与x的函数关系式为:,故选C.
9.B
【详解】
将△ABE绕点A逆时针旋转90°,得到△ADH,
因为四边形ABCD是正方形,
所以AB=BC=AD, ∠BAD=∠ABC=90°,∠ABD=∠CBD=45°,
在△BNA和△BNC中,
,
所以△BNA≌△BNC,
所以AN=CN,
∠NEC=∠NCE=∠BAN,
因为∠NEC+∠BEN=180°,
所以∠BAN+∠BEN=180°,
所以∠ABC+∠ANE=180°,
所以∠ANE=90°,
所以AN=NE,AN⊥NE,故①正确,
因为∠3=45°, ∠1=∠4,
所以∠2+∠4=∠2+∠1=45°,
所以∠3=∠FAH=45°,
因为AF=AF,AE=AH,
所以△AFE≌△AFH,
所以EF=FH=DF+DH=DF+BE, ∠AFH=∠AFE,故②正确,
因为∠MAN=∠NDF=45°, ∠ANM=∠NDF,
所以∠AMN=∠AFD,
又因为∠AFE=∠AFD, ∠DFE=∠AFE+∠AFD
所以∠DFE=2∠AMN,故③正确,
因为∠MAN=∠EAF, ∠AMN=∠AFE,
所以△AMN∽△AFE,
所以,
所以MN,
如图2中,将△ABN绕点A逆时针旋转90°,得到△ADG,
易证△ANG≌△ANM, △GDN是直角三角形,
所以MN=GN,
所以,
所以,故④正确,
图中相似三角形有△ANE∽△BAD∽△BCD, △ANM∽△AEF, △ABN∽△FDN,
△BEM∽△DAM等,故⑤错误,故选B.
10.B
【解析】
试题分析:∵,∴OA OD=2.∵D是AB的中点,∴AB=2AD,∴矩形的面积=OA AB=2AD OA=2×2=4.故选B.
考点:反比例函数系数k的几何意义.
11.
【解析】
因为二次函数与x轴的交点是关于对称轴对称的两点,根据对称性可得:抛物线的对称轴,故答案为:.
12.5
【详解】
根据题意,易得△MBA∽△MCO,
根据相似三角形的性质可知,即,解得AM=5.
∴小明的影长为5米.
13.3
【详解】
试题解析::∵抛物线的开口向上,顶点纵坐标为-3,
∴a>0.
-=-3,即b2=12a,
∵一元二次方程ax2+bx+m=0有实数根,
∴△=b2-4am≥0,即12a-4am≥0,即12-4m≥0,解得m≤3,
∴m的最大值为3,
14.
【解析】
因为BC=6,AF:FG:GD=3:2:1,所以AF=3,DG=1,
因为∠AFB=∠GFE,∠A=∠E=90°,
所以∠ABF=∠FGE,
又因为∠FGE=∠DGC,
所以∠ABF=∠DGC,
因为∠A=∠D=90°,
所以△AFB∽△DCG,
所以,
因为AB=CD,
所以即,
所以,
所以.
故答案为:.
15.或
【分析】
用含k的式子分别表示出,,,然后相加整理得到一个等式,对等式进行分析可得到k的值.
【详解】
解:,
,,
,
,
或,
当时,,
当时,,
所以,或.
故答案为:或.
【点睛】
本题考查了分式的化简求值,解题关键在于将式子变形为.
16.
【解析】
试题分析:根据已知条件二次函数的顶点坐标A(-1,4)可设二次函数顶点式即:
,然后根据二次函数经过点B(2, -5),代入可求得a=,然后代入解析式即可求解.
试题解析:由顶点A(-1,4),可设函数解析式为,
∵二次函数的图象过点B(2,-5),
∴,
解得,
∴二次函数解析式为.
17.(1)见解析;(2).
【解析】
试题分析:(1)先根据AB=AC,可证得△ABC是等腰三角形,由∠A=36°,可得∠ABC=∠C=72°,因为BD平分∠ABC交AC于点D,所以∠CBD=∠ABD=36°,
∠BDC=∠C =72°,根据等角对等边可得: AD=BD=BC, 根据∠CBD=∠A,∠C=∠C,
可判定△CBD∽△CAB,根据相似三角形对应边成比例可得:,即可求证
,(2)设AD=x,则CD=1-x,再根据,可得,
解得:.
试题解析:(1)∵AB=AC=1,∠A=36°,
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠CBD=∠ABD=36°,∠BDC=72°,
∴AD=BD=BC,
∵∠CBD=∠A,∠C=∠C,
∴△CBD∽△CAB,
∴,即
(2)由(1)得,点D是AC的一个黄金分割点,
∴AD=.
18.(1)见解析;(2)0≤z≤4.
【解析】
试题分析:先根据顶点坐标公式计算出函数(m为常数)的顶点坐标,然后把顶点坐标横坐标代入的图象上可求出对应的函数值,函数值与顶点坐标的纵坐标相等,即可证明,(2)把顶点纵坐标看成关于m的二次函数,然后根据二次函数图象性质,在﹣2≤m≤3范围内求出顶点坐标纵坐标的最大值和最小值,即可求解.
试题解析:∵的顶点坐标为 ,
把代入得:,
∴不论m为何值,该函数的图象的顶点都在函数的图象上,
(2)设函数,
当时,有最小值为0,
当时,随m的增大而减小,当m>﹣1时,z随m的增大而增大,
当m=﹣2时,z=,当m=3时,z=4,
∴当﹣2≤m≤3时,该函数图象的顶点纵坐标的取值范围是0≤z≤4.
19.(1)证明见解析;(2)证明见解析
【分析】
(1)根据等腰三角形的性质可得∠B=∠C,再由∠DEF+∠CEF=∠B+∠BDE,,即可判定,根据相似三角形的判定方法即可得△BDE∽△CEF;(2)由相似三角形的性质可得,再由点E是BC的中点,可得BE=CE,即可得,又因,即可判定△CEF∽△EDF,根据相似三角形的性质可得,即可证得即FE平分∠DFC.
【详解】
解:(1)因为AB=AC,所以∠B=∠C,
因为∠DEF+∠CEF=∠B+∠BDE,
所以,
所以△BDE∽△CEF;
(2)因为△BDE∽△CEF,所以,
因为点E是BC的中点,所以BE=CE,即,
所以,又,故△CEF∽△EDF,
所以,即FE平分∠DFC.
20.(1),;(2)P ,.
【详解】
试题分析:(1)由点A在一次函数图象上,结合一次函数解析式可求出点A的坐标,再由点A的坐标利用待定系数法即可求出反比例函数解析式,联立两函数解析式成方程组,解方程组即可求出点B坐标;
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,连接PB.由点B、D的对称性结合点B的坐标找出点D的坐标,设直线AD的解析式为y=mx+n,结合点A、D的坐标利用待定系数法求出直线AD的解析式,令直线AD的解析式中y=0求出点P的坐标,再通过分割图形结合三角形的面积公式即可得出结论.
试题解析:(1)把点A(1,a)代入一次函数y=-x+4,
得:a=-1+4,解得:a=3,
∴点A的坐标为(1,3).
把点A(1,3)代入反比例函数y=,
得:3=k,
∴反比例函数的表达式y=,
联立两个函数关系式成方程组得:,
解得:,或,
∴点B的坐标为(3,1).
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,连接PB,如图所示.
∵点B、D关于x轴对称,点B的坐标为(3,1),
∴点D的坐标为(3,- 1).
设直线AD的解析式为y=mx+n,
把A,D两点代入得:,
解得:,
∴直线AD的解析式为y=-2x+5.
令y=-2x+5中y=0,则-2x+5=0,
解得:x=,
∴点P的坐标为(,0).
S△PAB=S△ABD-S△PBD=BD (xB-xA)-BD (xB-xP)
=×[1-(-1)]×(3-1)-×[1-(-1)]×(3-)
=.
考点:1.反比例函数与一次函数的交点问题;2.待定系数法求一次函数解析式;3.轴对称-最短路线问题.
21.(1)函数关系为p=﹣30x+1500;(2)这批农产品的销售价格定为40元,才能使日销售利润最大;(3)a的值为2.
【分析】
(1)首先根据表中的数据,可猜想y与x是一次函数关系,任选两点求表达式,再验证猜想的正确性;
(2)根据题意列出日销售利润w与销售价格x之间的函数关系式,根据二次函数的性质确定最大值即可;
(3)根据题意列出日销售利润w与销售价格x之间的函数关系式,并求得抛物线的对称轴,再分两种情况进行讨论,依据二次函数的性质求得a的值.
【详解】
(1)假设p与x成一次函数关系,设函数关系式为p=kx+b,
则,
解得:k=﹣30,b=1500,
∴p=﹣30x+1500,
检验:当x=35,p=450;当x=45,p=150;当x=50,p=0,符合一次函数解析式,
∴所求的函数关系为p=﹣30x+1500;
(2)设日销售利润w=p(x﹣30)=(﹣30x+1500)(x﹣30)
即w=﹣30x2+2400x﹣45000,
∴当x=﹣=40时,w有最大值3000元,
故这批农产品的销售价格定为40元,才能使日销售利润最大;
(3)日获利w=p(x﹣30﹣a)=(﹣30x+1500)(x﹣30﹣a),
即w=﹣30x2+(2400+30a)x﹣(1500a+45000),
对称轴为x=﹣=40+a,
①若a≥10,则当x=45时,w有最大值,
即w=2250﹣150a<2430(不合题意);
②若a<10,则当x=40+a时,w有最大值,
将x=40+a代入,可得w=30(a2﹣10a+100),
当w=2430时,2430=30(a2﹣10a+100),
解得a1=2,a2=-38(舍去),
综上所述,a的值为2.
【点睛】
本题主要考查二次函数的应用,解题的关键是:
(1) 首先根据表中的数据,可猜想y与x是一次函数关系, 任选两点求表达式,再验证猜想的正确性;
(2)根据题意列出日销售利润w与销售价格x之间的函数关系式,根据二次函数的性质确定最大值即可;
(3)根据题意列出日销售利润w与销售价格x之间的函数关系式,并求得抛物线的对称轴,再分两种情况进行讨论,依据二次函数的性质求得a的值.
22.(1)8 (2)6
【分析】
(1)由DE∥BC,得到△ADE∽△ABC,根据相似三角形的性质得到,代入数据即可得到结论;
(2)根据平行线的性质得到AF⊥DE,根据DE∥BC,推出△ADG∽△ABF,根据相似三角形的性质得到,代入数据即可得到结论.
【详解】
解:(1)∵,
∴∽,
∴,
∵,,,
∴,
∴;
(2)∵是的高,
∴,
∵,
∴,
∵,
∴∽,
∴,
∵,
∴,
∴,
即点到的距离是6.
【点睛】
本题考查了相似三角形的判定和性质,平行线的性质,熟练掌握相似三角形的判定和性质是解题的关键.
23.CD=2.
【分析】
根据三角形相似的性质求解即可.
【详解】
∵△ADE∽△ABC,
∴.
∵AD=6,AE=4,AB=12,
∴.
∴AC=8.
∴CD=AC-AD=8-6=2.
【点睛】
本题考查的是相似三角形的性质,熟知相似三角形的对应边成比例是解答此题的关键.
24.(1)y2=-;(2)S△AOB=;(3)当x<3时,y2>0或y2<-4.
【解析】
【分析】
(1)过点A作AE⊥轴于点E,在Rt△AEO中,通过解直角三角形可求出点A的坐标,由反比例函数图象上点的坐标特征即可求出反比例函数的解析式;
(2)由反比例函数图象上点的坐标特征可求出点B的坐标,根据点A、B的坐标,利用待定系数法可求出直线AB的解析式,再根据一次函数图象上点的坐标特征可求出点C的坐标,利用三角形的面积公式即可求出△AOB的面积;
(3)观察函数图象可得出:<0以及0<<3时,的取值范围,合在一起即可得出结论.
【详解】
解:(1)过点A作AE⊥x轴于点E,如图所示.
在Rt△AEO中,AO=5,sin∠AOC=,
∴AE=AO sin∠AOC=5×=3,
∴OE==4,
∴点A的坐标为(-4,3).
∵点A在反比例函数y2=的图象上,
∴k2=-4×3=-12,
∴反比例函数的解析式为y2=-.
(2)∵点B(m,-4)反比例函数y2=-的图象上,
∴-4=-,解得:m=3,
∴点B的坐标为(3,-4).
将A(-4,3)、B(3,-4)代入y1=k1x+b中,
,解得:,
∴直线AB的解析式为y=-x-1.
当y=-x-1=0时,x=-1,
∴点C的坐标为(-1,0),
∴S△AOB=OC (yA-yB)=×1×[3-(-4)]=.
(3)观察函数图象可知:当x<0时,y2>0;当0<x<3时,y2<-4.
∴当x<3时,y2>0或y2<-4.
【点睛】
本题考查了反比例函数与一次函数的交点问题、待定系数法求一次函数解析式、反比例(一次)函数图象上点的坐标特征以及三角形的面积,解题的关键是:(1)通过解直角三角形找出点A的坐标;(2)根据点A、B的坐标,利用待定系数法求出直线AB的解析式;(3)观察函数图象,找出当<m时,的取值范围.
(
2
)
(
1
)
同课章节目录
