沪科版九年级上册数学期中复习培优试卷(含解析)
文档属性
| 名称 | 沪科版九年级上册数学期中复习培优试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 523.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 16:38:35 | ||
图片预览




文档简介
沪科版九年级上册数学期中复习培优试卷
一、选择题。(每小题只有一个正确答案)
1.抛物线的对称轴是( )
A.直线 B.直线 C.轴 D.直线
2.已知(5,-1)是双曲线上的一点,则下列各点中不在该图象上的是( )
A. B. C. D.
3.已知x:y=5:2,则下列各式中不正确的是( )
A. B. C. D.
4.在同一直角坐标系中,一次函数和二次函数的图象大致为
A. B. C. D.
5.若∽,其面积比为,则与的相似比为( )
A. B. C. D.
6.已知:如图,在△ABC中,∠ADE=∠C,则下列等式成立的是 ( )
A. B. C. D.
7.已知,那么( )
A.a是b 、c 的比例中项 B.c是a、b的比例中项
C.b是a、c的比例中项 D.以上都不对
8.函数的图象上有两点,,若,则( )
A. B.
C. D.的大小不确定
9.将抛物线的图象向右平移2个单位,再向下平移3个单位,得到的抛物线是
A. B.
C. D.
10.如图,在中,,,,点是上的一个动点(不与、两点重合),于点,于点,点从靠近点的某一点向点移动,矩形的周长变化情况是( )
A.逐渐减小 B.逐渐增大 C.先增大后减小 D.先减小后增大
二、填空题
11.已知、是线段的两个黄金分割点,且,则长为_________
12.已知抛物线的顶点在y轴上,k的值______________.
13.教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为,由此可知铅球推出的距离是______m.
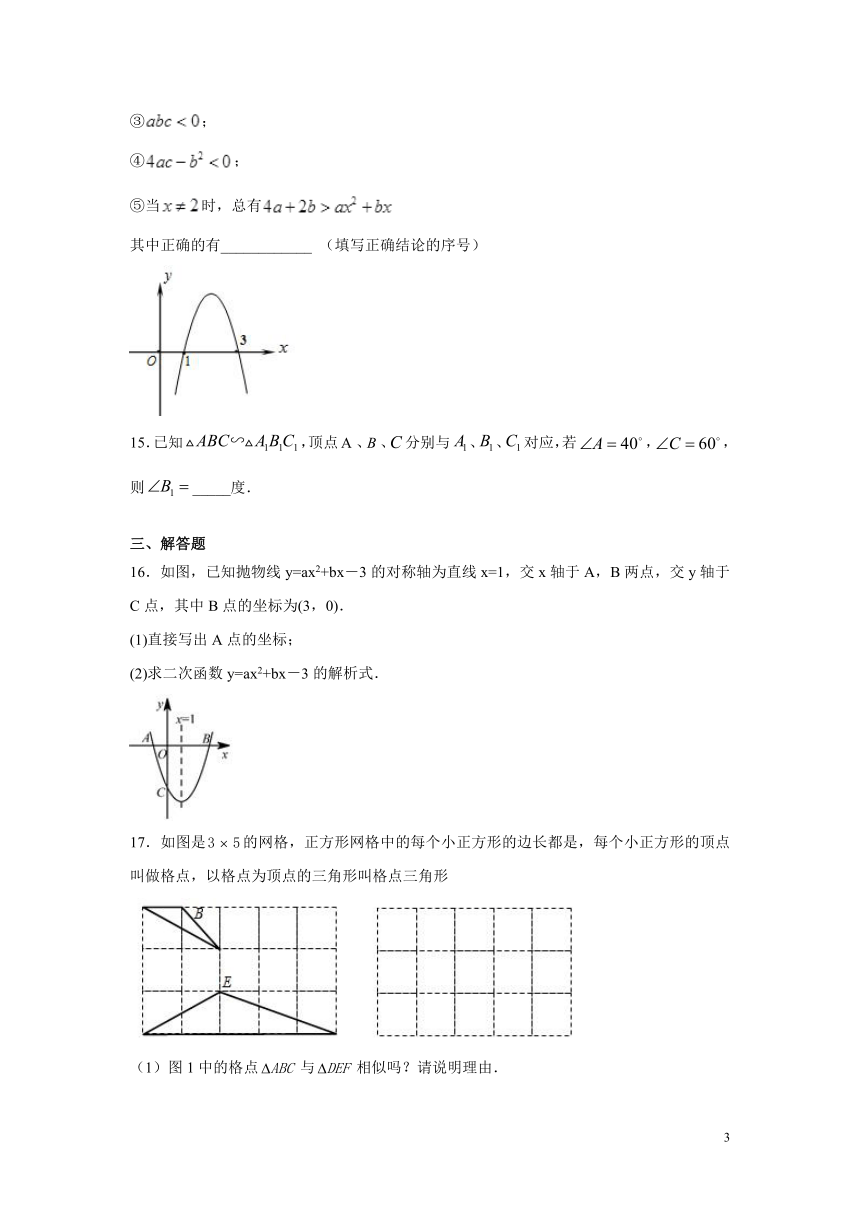
14.二次函数的图象如图所示,以下结论:
①;
②;
③;
④;
⑤当时,总有
其中正确的有____________ (填写正确结论的序号)
15.已知,顶点、、分别与、、对应,若,,则_____度.
三、解答题
16.如图,已知抛物线y=ax2+bx-3的对称轴为直线x=1,交x轴于A,B两点,交y轴于C点,其中B点的坐标为(3,0).
(1)直接写出A点的坐标;
(2)求二次函数y=ax2+bx-3的解析式.
17.如图是的网格,正方形网格中的每个小正方形的边长都是,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫格点三角形
(1)图1中的格点与相似吗?请说明理由.
(2)请在图2中画一个格点与相似(注意:与、都不全等)
18.已知函数(为常数).
(1)证明:无论m取何值,该函数与轴总有两个交点;
(2)设函数的两交点的横坐标分别为和,且,求此函数的解析式.
19.如图,一次函数与反比例函数的图象交于、两点.
(1)求、两点的坐标和反比例函数的解析式;
(2)根据图象,直接写出当时的取值范围;
(3)求的面积.
20.如图,在等腰三角形中,,是边上一点,以为一边,向上作等腰,使,连,求证:
(1); (2).
21.为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)x为何值时,y有最大值?最大值是多少?
22.如图,是等边三角形,点、分别在、上,且,与相交于点.
(1)证明:≌;
(2)与相似吗?说说你的理由;
(3)吗?请说明理由.
23.如图,反比例函数的图象经过点A(,4),直线()与双曲线在第二、四象限分别相交于P,Q 两点,与x轴、y 轴分别相交于C,D 两点.
(1)求k 的值;
(2)当时,求△OCD 的面积;
(3)连接OQ,是否存在实数b,使得? 若存在,请求出b 的值;若不存在,请说明理由.
参考答案
1.C
【解析】
试题分析:因为二次函数的对称轴是y轴,所以抛物线的对称轴是y轴,故选;C.
考点:二次函数的对称轴.
2.B
【详解】
解:因为点(5,-1)是双曲线上的一点,
将(5,-1)代入得k=-5;
四个选项中只有B不符合要求:k=5×1≠-5.
故选B.
【点睛】
本题考查反比例函数图象上点的坐标特征.
3.B
【解析】
试题解析:A、由合比性质得,,故A正确;
B、由反比性质,得y:x=2:5.由分比性质得,再由反比性质得,故B错误;
C、由反比性质,得y:x=2:5.由合比性质得,再由反比性质得,故C正确;
D、由分比性质,得,故D正确;
故选B.
考点:比例的性质.
4.B
【解析】
试题分析:A、由一次函数y=ax+c的图象可得,a>0,c>0,此时二次函数y=ax2+c开口应向上,所以A错误;B、由一次函数y=ax+c可得,a<0,c>0,二次函数y=ax2+c开口应向下,在y轴上与一次函数交于同一点,符合;C、由一次函数y=ax+c可得,a<0,c<0,二次函数y=ax2+c开口应向下,与图不符;
D、一次函数y=ax+c和二次函数y=ax2+c常数项相同,在y轴上应交于同一点,与图不符;故选B.
考点:1.一次函数图像的性质、2.二次函数图像的性质.
5.D
【解析】
试题分析:因为∽,且其面积比为,所以根据相似三角形的性质可得:与的相似比为,故选:D.
考点:相似三角形的性质.
6.C
【解析】
【分析】
试题分析:,又,所以△AEC∽△ABC,所以
故选C,考点:相似三角形各边之比
点评:相似三角形各边之比为常数,相等的角相对应的边成比例.
【详解】
请在此输入详解!
7.C
【解析】
试题分析:因为,所以,所以b是a、c的比例中项,故选C.
考点:比例中项
8.B
【解析】
试题分析:因为,所以对称轴为,又<0,抛物线开口向下,所以当x>-4时,y随x的增大而减小,因为,所以,故选:B.
考点:抛物线的性质.
9.D
【解析】
试题分析:根据抛物线的平移规律:左加右减,上加下减,所以将抛物线的图象向右平移2个单位得,,再向下平移3个单位,得到的抛物线是,故选;D.
考点:抛物线的平移.
10.A
【详解】
试题分析:设DE=x,DF=y,因为,,,所以AB=10,又,,所以根据题意可得:△ADE∽ABC,△BDF∽BAC,所以,所以,所以,所以(0<x<10),所以矩形的周长l=2x+2y=2x+2()=,所以l的值随着x的值的增大而减小,因为点从靠近点的某一点向点移动时,x的值逐渐增大,所以矩形的周长逐渐减小,故选A.
考点:1.相似三角形的判定性质、2.一次函数的应用.
11.10-20
【分析】
首先根据题意画出图形,由P、Q是线段AB的两个黄金分割点,可求得AQ与BP的长,继而求得答案.
【详解】
根据黄金分割点的概念,可知AQ=BP=×10=(5 5)cm.
则PQ=AQ+BP AB=(5 5)×2 10=(10 20)cm,
故本题答案为:(10 20).
【点睛】
本题考查了黄金分割,熟练掌握黄金分割点是解题的关键.
12.-2
【解析】
试题分析:因为抛物线的顶点在轴上,所以抛物线的对称轴是y轴,所以,所以k= -2.
考点:抛物线的性质.
13.10
【分析】
要求铅球推出的距离,实际上是求铅球的落脚点与坐标原点的距离,故可直接令,求出x的值,x的正值即为所求.
【详解】
在函数式中,令,得
,解得,(舍去),
∴铅球推出的距离是10m.
【点睛】
本题是二次函数的实际应用题,需要注意的是中3代表的含义是铅球在起始位置距离地面的高度;当时,x的正值代表的是铅球最终离原点的距离.
14.①②④⑤
【解析】
试题分析:观察图形可知二次函数的图象过点(1,0),所以,所以①正确;又因为二次函数的图象过点(3,0),所以对称轴是x=2,所以,所以b=-4a,所以,所以②正确;因为抛物线开口向下,所以a<0,因为对称轴是x=2,所以a、b异号,所以b>0,因为抛物线与y轴交于负半轴,所以c<0,所以abc>0,所以③错误;因为二次函数的图象与z轴有两个交点,所以>0,所以,因此④正确;因为当x=2时,y有最大值,所以当时,总有,因此⑤正确;所以正确的有①②④⑤.
考点:二次函数图象的性质.
15.80
【分析】
由∠A=40°,∠C=60°,根据三角形的内角和定理,即可求得∠B的度数,又由△ABC∽△A1B1C1,根据相似三角形的对应角相等,即可求得∠B1的度数.
【详解】
解:∵∠A=40°,∠C=60°,
∴∠B=180°-∠A-∠C=80°,
∵△ABC∽△A1B1C1,
∴∠B1=∠B=80°.
故答案为80.
【点睛】
此题考查了相似三角形的性质与三角形内角和定理.解题的关键是注意掌握相似三角形的对应角相等.
16.(1)(-1,0);(2)
【分析】
(1)由抛物线y=ax2+bx-3的对称轴为直线x=1,交x轴于A、B两点,其中B点的坐标为(3,0),根据二次函数的对称性,即可求得A点的坐标;
(2)利用待定系数法,将A(-1,0)、B(3,0)两点的坐标代入y=ax2+bx-3,即可求得二次函数y=ax2+bx-3的解析式.
【详解】
(1)∵抛物线对称轴为直线,
交轴于A、B两点,其中B点坐标为(3,0),
∴A点横坐标为:,
∴A点坐标为:(-1,0)
(2)将A(-1,0),B(3,0)代入得
解得:
故抛物线解析式为:
考点:1.待定系数法,2.二次函数的解析式
17.(1)△ABC∽△DEF,理由见解析(2)见解析
【解析】
试题分析:(1)分别求出两个三角形的三边的长,然后利用相似三角形的判定定理证明即可;(2)在图2中画一个边长分别为的三角形即可.
试题解析:(1)△ABC∽△DEF,理由如下:
由图可知:,,,,,
则,
∴△ABC∽△DEF;
(2)△如图所示。
考点:相似三角形的判定.
18.(1)见解析(2)y=x2-2x-8.
【解析】
试题分析:(1)证明△=b2-4ac>0即可;(2)利用根与系数的关系得到x1+x2=2m,x1x2=-2(m+3)代入,解方程得出m=1即可.
试题解析:(1)令y=0,得△=(-2m)2-4[-2(m+3)]=4(m+1)2+20>0
∴无论m取何值,方程x2-2mx-2(m+3)=0总有两个不相等的实数根.
即无论m取何值,该函数与轴总有两个交点.
(2)依题意有x1+x2=2m,x1x2=-2(m+3)
由,解得m=1.∴函数的解析式为y=x2-2x-8.
考点:二次函数与一元二次方程.
19.(1)A(1,4)、B(4,1),;(2)x<0或1<x<4;(3)
【解析】
试题分析:(1)把A(1,m)、B(4,n)代入,即可求出两点的坐标,然后把点A的坐标代入,即可求出反比例函数的解析式;(2)根据函数图象直接作答即可;(3)作AC⊥x轴于C,BD⊥x轴于D,然后根据计算即可.
试题解析:(1)将A(1,m)、B(4,n)代入,得 ,
∴A、B两点的坐标是A(1,4)、B(4,1)
把A(1,4)代入,得,故反比例函数的解析式为。
(2)由图象,得所求的x取值范围是:x<0或1<x<4
(3)作AC⊥x轴于C,BD⊥x轴于D. 则
∴= =
考点:1.一次函数、2.反比例函数与一元一次方程、3.函数图象的性质与不等式.
20.(1)见解析(2)见解析
【解析】
试题分析:(1)由得到,然后利用角的和差关系即可证明;(2)根据条件证明∽得到,再由得到,从而得出,然后可证明结论.
试题解析: (1)
∴
(2)
∴∽
∴
∴
∴
∴
考点:相似三角形的判定与性质.
21.(1)(0<x<40);(2)当x=20时,y有最大值,最大值是300平方米.
【详解】
试题分析:(1)根据三个矩形面积相等,得到矩形AEFD面积是矩形BCFE面积的2倍,可得出AE=2BE,设BE=a,则有AE=2a,表示出a与2a,进而表示出y与x的关系式,并求出x的范围即可;
(2)利用二次函数的性质求出y的最大值,以及此时x的值即可.
试题解析:(1)∵三块矩形区域的面积相等,
∴矩形AEFD面积是矩形BCFE面积的2倍,
∴AE=2BE,
设BE=a,则AE=2a,
∴8a+2x=80,
∴a=-x+10,3a=-x+30,
∴y=(-x+30)x=-x2+30x,
∵a=-x+10>0,
∴x<40,
则y=-x2+30x(0<x<40);
(2)∵y=-x2+30x=-(x-20)2+300(0<x<40),且二次项系数为-<0,
∴当x=20时,y有最大值,最大值为300平方米.
考点:二次函数的应用.
22.(1)见解析 (2)见解析 (3)见解析
【分析】
(1)根据等边三角形的性质,利用SAS证得△ABD≌△BCE;
(2)由△ABD≌△BCE得∠BAD=∠CBE,然后可证,结合公共角,由此可以证明△AEF∽△BEA;
(3)由,结合公共角,证明∽,然后可以得到,即BD2=AD DF.
【详解】
(1)在与中,
∵,,,
∴≌;
(2)由≌,得,
∵,
∴,
∵是与的公共角,
∴∽;
(3)∵,是与的公共角,
∴∽,
∴,即.
【点睛】
本题考查了全等三角形的判定和性质、等边三角形的性质以及相似三角形的判定和性质,有一定的综合性,熟练掌握相关性质定理是解题关键.
23.(1);(2)2;(3).
【解析】
试题分析:(1)把A(-1,4)代入双曲线的解析式即可;
(2)由,可得到直线CD的解析式为,从而得出CO=DO=2,即可得到的值;
(3)过Q作QE⊥y轴,垂足为E.然后分①b<0和②b>0两种情况讨论.当b<0时,由可知, OC=OD,∠OCD=∠ODC=45°,所以∠EDQ=∠DQE=45°,得到DE=EQ,由,可得到CO=QE,从而有Q(-b,2b),由点Q在双曲线的图象上,得到,即可得到b的值;②当b>0时,有,综和这两种情况,得到b的值.
试题解析:(1)∵A(-1,4)在双曲线上,∴;
(2)∵,∴直线CD的解析式为,∴C(-2,0),D(0,-2),∴CO=2,DO=2,∴=CO·DO=2;
(3)过Q作QE⊥y轴,垂足为E.
①当b<0时,由可知,C(b,0),D(0,b),∴OC=OD,∴∠OCD=∠ODC=45°,∴∠EDQ=∠DQE=45°,∴DE=EQ,∵,∴CO·DO=DO·QE,∴CO=QE,∴Q(-b,2b),∵点Q在双曲线的图象上,∴,∴,∴,∵b<0,∴;
②当b>0时,此时;
综上所述,当时,.
考点:反比例函数与一次函数的交点问题.
(
2
)
(
1
)
一、选择题。(每小题只有一个正确答案)
1.抛物线的对称轴是( )
A.直线 B.直线 C.轴 D.直线
2.已知(5,-1)是双曲线上的一点,则下列各点中不在该图象上的是( )
A. B. C. D.
3.已知x:y=5:2,则下列各式中不正确的是( )
A. B. C. D.
4.在同一直角坐标系中,一次函数和二次函数的图象大致为
A. B. C. D.
5.若∽,其面积比为,则与的相似比为( )
A. B. C. D.
6.已知:如图,在△ABC中,∠ADE=∠C,则下列等式成立的是 ( )
A. B. C. D.
7.已知,那么( )
A.a是b 、c 的比例中项 B.c是a、b的比例中项
C.b是a、c的比例中项 D.以上都不对
8.函数的图象上有两点,,若,则( )
A. B.
C. D.的大小不确定
9.将抛物线的图象向右平移2个单位,再向下平移3个单位,得到的抛物线是
A. B.
C. D.
10.如图,在中,,,,点是上的一个动点(不与、两点重合),于点,于点,点从靠近点的某一点向点移动,矩形的周长变化情况是( )
A.逐渐减小 B.逐渐增大 C.先增大后减小 D.先减小后增大
二、填空题
11.已知、是线段的两个黄金分割点,且,则长为_________
12.已知抛物线的顶点在y轴上,k的值______________.
13.教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为,由此可知铅球推出的距离是______m.
14.二次函数的图象如图所示,以下结论:
①;
②;
③;
④;
⑤当时,总有
其中正确的有____________ (填写正确结论的序号)
15.已知,顶点、、分别与、、对应,若,,则_____度.
三、解答题
16.如图,已知抛物线y=ax2+bx-3的对称轴为直线x=1,交x轴于A,B两点,交y轴于C点,其中B点的坐标为(3,0).
(1)直接写出A点的坐标;
(2)求二次函数y=ax2+bx-3的解析式.
17.如图是的网格,正方形网格中的每个小正方形的边长都是,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫格点三角形
(1)图1中的格点与相似吗?请说明理由.
(2)请在图2中画一个格点与相似(注意:与、都不全等)
18.已知函数(为常数).
(1)证明:无论m取何值,该函数与轴总有两个交点;
(2)设函数的两交点的横坐标分别为和,且,求此函数的解析式.
19.如图,一次函数与反比例函数的图象交于、两点.
(1)求、两点的坐标和反比例函数的解析式;
(2)根据图象,直接写出当时的取值范围;
(3)求的面积.
20.如图,在等腰三角形中,,是边上一点,以为一边,向上作等腰,使,连,求证:
(1); (2).
21.为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)x为何值时,y有最大值?最大值是多少?
22.如图,是等边三角形,点、分别在、上,且,与相交于点.
(1)证明:≌;
(2)与相似吗?说说你的理由;
(3)吗?请说明理由.
23.如图,反比例函数的图象经过点A(,4),直线()与双曲线在第二、四象限分别相交于P,Q 两点,与x轴、y 轴分别相交于C,D 两点.
(1)求k 的值;
(2)当时,求△OCD 的面积;
(3)连接OQ,是否存在实数b,使得? 若存在,请求出b 的值;若不存在,请说明理由.
参考答案
1.C
【解析】
试题分析:因为二次函数的对称轴是y轴,所以抛物线的对称轴是y轴,故选;C.
考点:二次函数的对称轴.
2.B
【详解】
解:因为点(5,-1)是双曲线上的一点,
将(5,-1)代入得k=-5;
四个选项中只有B不符合要求:k=5×1≠-5.
故选B.
【点睛】
本题考查反比例函数图象上点的坐标特征.
3.B
【解析】
试题解析:A、由合比性质得,,故A正确;
B、由反比性质,得y:x=2:5.由分比性质得,再由反比性质得,故B错误;
C、由反比性质,得y:x=2:5.由合比性质得,再由反比性质得,故C正确;
D、由分比性质,得,故D正确;
故选B.
考点:比例的性质.
4.B
【解析】
试题分析:A、由一次函数y=ax+c的图象可得,a>0,c>0,此时二次函数y=ax2+c开口应向上,所以A错误;B、由一次函数y=ax+c可得,a<0,c>0,二次函数y=ax2+c开口应向下,在y轴上与一次函数交于同一点,符合;C、由一次函数y=ax+c可得,a<0,c<0,二次函数y=ax2+c开口应向下,与图不符;
D、一次函数y=ax+c和二次函数y=ax2+c常数项相同,在y轴上应交于同一点,与图不符;故选B.
考点:1.一次函数图像的性质、2.二次函数图像的性质.
5.D
【解析】
试题分析:因为∽,且其面积比为,所以根据相似三角形的性质可得:与的相似比为,故选:D.
考点:相似三角形的性质.
6.C
【解析】
【分析】
试题分析:,又,所以△AEC∽△ABC,所以
故选C,考点:相似三角形各边之比
点评:相似三角形各边之比为常数,相等的角相对应的边成比例.
【详解】
请在此输入详解!
7.C
【解析】
试题分析:因为,所以,所以b是a、c的比例中项,故选C.
考点:比例中项
8.B
【解析】
试题分析:因为,所以对称轴为,又<0,抛物线开口向下,所以当x>-4时,y随x的增大而减小,因为,所以,故选:B.
考点:抛物线的性质.
9.D
【解析】
试题分析:根据抛物线的平移规律:左加右减,上加下减,所以将抛物线的图象向右平移2个单位得,,再向下平移3个单位,得到的抛物线是,故选;D.
考点:抛物线的平移.
10.A
【详解】
试题分析:设DE=x,DF=y,因为,,,所以AB=10,又,,所以根据题意可得:△ADE∽ABC,△BDF∽BAC,所以,所以,所以,所以(0<x<10),所以矩形的周长l=2x+2y=2x+2()=,所以l的值随着x的值的增大而减小,因为点从靠近点的某一点向点移动时,x的值逐渐增大,所以矩形的周长逐渐减小,故选A.
考点:1.相似三角形的判定性质、2.一次函数的应用.
11.10-20
【分析】
首先根据题意画出图形,由P、Q是线段AB的两个黄金分割点,可求得AQ与BP的长,继而求得答案.
【详解】
根据黄金分割点的概念,可知AQ=BP=×10=(5 5)cm.
则PQ=AQ+BP AB=(5 5)×2 10=(10 20)cm,
故本题答案为:(10 20).
【点睛】
本题考查了黄金分割,熟练掌握黄金分割点是解题的关键.
12.-2
【解析】
试题分析:因为抛物线的顶点在轴上,所以抛物线的对称轴是y轴,所以,所以k= -2.
考点:抛物线的性质.
13.10
【分析】
要求铅球推出的距离,实际上是求铅球的落脚点与坐标原点的距离,故可直接令,求出x的值,x的正值即为所求.
【详解】
在函数式中,令,得
,解得,(舍去),
∴铅球推出的距离是10m.
【点睛】
本题是二次函数的实际应用题,需要注意的是中3代表的含义是铅球在起始位置距离地面的高度;当时,x的正值代表的是铅球最终离原点的距离.
14.①②④⑤
【解析】
试题分析:观察图形可知二次函数的图象过点(1,0),所以,所以①正确;又因为二次函数的图象过点(3,0),所以对称轴是x=2,所以,所以b=-4a,所以,所以②正确;因为抛物线开口向下,所以a<0,因为对称轴是x=2,所以a、b异号,所以b>0,因为抛物线与y轴交于负半轴,所以c<0,所以abc>0,所以③错误;因为二次函数的图象与z轴有两个交点,所以>0,所以,因此④正确;因为当x=2时,y有最大值,所以当时,总有,因此⑤正确;所以正确的有①②④⑤.
考点:二次函数图象的性质.
15.80
【分析】
由∠A=40°,∠C=60°,根据三角形的内角和定理,即可求得∠B的度数,又由△ABC∽△A1B1C1,根据相似三角形的对应角相等,即可求得∠B1的度数.
【详解】
解:∵∠A=40°,∠C=60°,
∴∠B=180°-∠A-∠C=80°,
∵△ABC∽△A1B1C1,
∴∠B1=∠B=80°.
故答案为80.
【点睛】
此题考查了相似三角形的性质与三角形内角和定理.解题的关键是注意掌握相似三角形的对应角相等.
16.(1)(-1,0);(2)
【分析】
(1)由抛物线y=ax2+bx-3的对称轴为直线x=1,交x轴于A、B两点,其中B点的坐标为(3,0),根据二次函数的对称性,即可求得A点的坐标;
(2)利用待定系数法,将A(-1,0)、B(3,0)两点的坐标代入y=ax2+bx-3,即可求得二次函数y=ax2+bx-3的解析式.
【详解】
(1)∵抛物线对称轴为直线,
交轴于A、B两点,其中B点坐标为(3,0),
∴A点横坐标为:,
∴A点坐标为:(-1,0)
(2)将A(-1,0),B(3,0)代入得
解得:
故抛物线解析式为:
考点:1.待定系数法,2.二次函数的解析式
17.(1)△ABC∽△DEF,理由见解析(2)见解析
【解析】
试题分析:(1)分别求出两个三角形的三边的长,然后利用相似三角形的判定定理证明即可;(2)在图2中画一个边长分别为的三角形即可.
试题解析:(1)△ABC∽△DEF,理由如下:
由图可知:,,,,,
则,
∴△ABC∽△DEF;
(2)△如图所示。
考点:相似三角形的判定.
18.(1)见解析(2)y=x2-2x-8.
【解析】
试题分析:(1)证明△=b2-4ac>0即可;(2)利用根与系数的关系得到x1+x2=2m,x1x2=-2(m+3)代入,解方程得出m=1即可.
试题解析:(1)令y=0,得△=(-2m)2-4[-2(m+3)]=4(m+1)2+20>0
∴无论m取何值,方程x2-2mx-2(m+3)=0总有两个不相等的实数根.
即无论m取何值,该函数与轴总有两个交点.
(2)依题意有x1+x2=2m,x1x2=-2(m+3)
由,解得m=1.∴函数的解析式为y=x2-2x-8.
考点:二次函数与一元二次方程.
19.(1)A(1,4)、B(4,1),;(2)x<0或1<x<4;(3)
【解析】
试题分析:(1)把A(1,m)、B(4,n)代入,即可求出两点的坐标,然后把点A的坐标代入,即可求出反比例函数的解析式;(2)根据函数图象直接作答即可;(3)作AC⊥x轴于C,BD⊥x轴于D,然后根据计算即可.
试题解析:(1)将A(1,m)、B(4,n)代入,得 ,
∴A、B两点的坐标是A(1,4)、B(4,1)
把A(1,4)代入,得,故反比例函数的解析式为。
(2)由图象,得所求的x取值范围是:x<0或1<x<4
(3)作AC⊥x轴于C,BD⊥x轴于D. 则
∴= =
考点:1.一次函数、2.反比例函数与一元一次方程、3.函数图象的性质与不等式.
20.(1)见解析(2)见解析
【解析】
试题分析:(1)由得到,然后利用角的和差关系即可证明;(2)根据条件证明∽得到,再由得到,从而得出,然后可证明结论.
试题解析: (1)
∴
(2)
∴∽
∴
∴
∴
∴
考点:相似三角形的判定与性质.
21.(1)(0<x<40);(2)当x=20时,y有最大值,最大值是300平方米.
【详解】
试题分析:(1)根据三个矩形面积相等,得到矩形AEFD面积是矩形BCFE面积的2倍,可得出AE=2BE,设BE=a,则有AE=2a,表示出a与2a,进而表示出y与x的关系式,并求出x的范围即可;
(2)利用二次函数的性质求出y的最大值,以及此时x的值即可.
试题解析:(1)∵三块矩形区域的面积相等,
∴矩形AEFD面积是矩形BCFE面积的2倍,
∴AE=2BE,
设BE=a,则AE=2a,
∴8a+2x=80,
∴a=-x+10,3a=-x+30,
∴y=(-x+30)x=-x2+30x,
∵a=-x+10>0,
∴x<40,
则y=-x2+30x(0<x<40);
(2)∵y=-x2+30x=-(x-20)2+300(0<x<40),且二次项系数为-<0,
∴当x=20时,y有最大值,最大值为300平方米.
考点:二次函数的应用.
22.(1)见解析 (2)见解析 (3)见解析
【分析】
(1)根据等边三角形的性质,利用SAS证得△ABD≌△BCE;
(2)由△ABD≌△BCE得∠BAD=∠CBE,然后可证,结合公共角,由此可以证明△AEF∽△BEA;
(3)由,结合公共角,证明∽,然后可以得到,即BD2=AD DF.
【详解】
(1)在与中,
∵,,,
∴≌;
(2)由≌,得,
∵,
∴,
∵是与的公共角,
∴∽;
(3)∵,是与的公共角,
∴∽,
∴,即.
【点睛】
本题考查了全等三角形的判定和性质、等边三角形的性质以及相似三角形的判定和性质,有一定的综合性,熟练掌握相关性质定理是解题关键.
23.(1);(2)2;(3).
【解析】
试题分析:(1)把A(-1,4)代入双曲线的解析式即可;
(2)由,可得到直线CD的解析式为,从而得出CO=DO=2,即可得到的值;
(3)过Q作QE⊥y轴,垂足为E.然后分①b<0和②b>0两种情况讨论.当b<0时,由可知, OC=OD,∠OCD=∠ODC=45°,所以∠EDQ=∠DQE=45°,得到DE=EQ,由,可得到CO=QE,从而有Q(-b,2b),由点Q在双曲线的图象上,得到,即可得到b的值;②当b>0时,有,综和这两种情况,得到b的值.
试题解析:(1)∵A(-1,4)在双曲线上,∴;
(2)∵,∴直线CD的解析式为,∴C(-2,0),D(0,-2),∴CO=2,DO=2,∴=CO·DO=2;
(3)过Q作QE⊥y轴,垂足为E.
①当b<0时,由可知,C(b,0),D(0,b),∴OC=OD,∴∠OCD=∠ODC=45°,∴∠EDQ=∠DQE=45°,∴DE=EQ,∵,∴CO·DO=DO·QE,∴CO=QE,∴Q(-b,2b),∵点Q在双曲线的图象上,∴,∴,∴,∵b<0,∴;
②当b>0时,此时;
综上所述,当时,.
考点:反比例函数与一次函数的交点问题.
(
2
)
(
1
)
同课章节目录
