沪科版九年级上册数学期中复习培优试题(含解析)
文档属性
| 名称 | 沪科版九年级上册数学期中复习培优试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 735.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 17:24:56 | ||
图片预览


文档简介
沪科版九年级上册数学期中复习培优试题
一、选择题。(每小题只有一个正确答案)
1.二次函数的对称轴是
A.直线 B.直线 C.y轴 D.x轴
2.若,则的值为( )
A.1 B. C. D.
3.已知二次函数y=(x-1)2-3,则此二次函数( )
A.有最大值1 B.有最小值1
C.有最大值-3 D.有最小值-3
4.将抛物线向右平移2个单位,再向下平移1个单位,则平移后抛物线的顶点坐标是( )
A.(2,1) B.(2,-1) C.(-2,-1) D.(-2,1)
5.如图,线段相交于点.若,则的长为( )
A. B. C. D.
6.如图,在平面直角坐标系中有两点,如果抛物线与线段有公共点,那么的取值范围是( )
A. B. C. D.
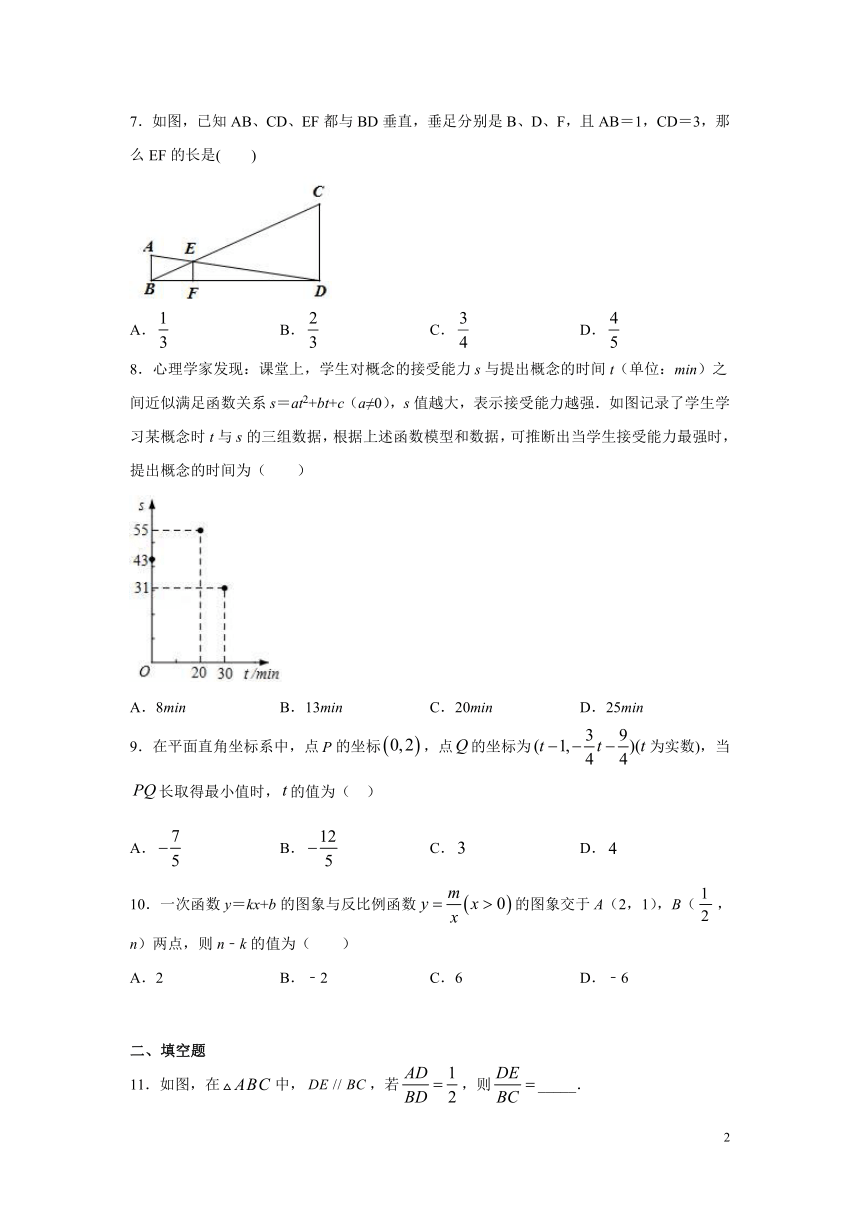
7.如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
A. B. C. D.
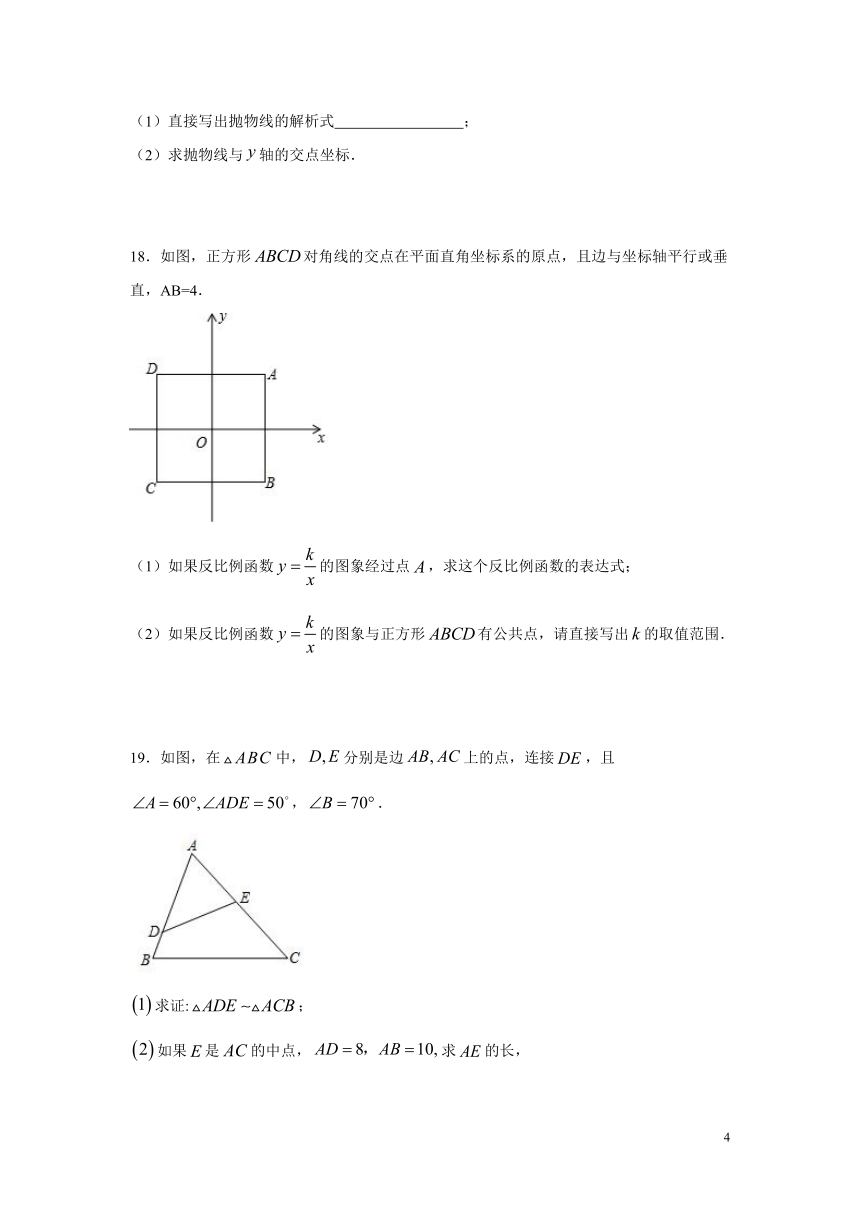
8.心理学家发现:课堂上,学生对概念的接受能力s与提出概念的时间t(单位:min)之间近似满足函数关系s=at2+bt+c(a≠0),s值越大,表示接受能力越强.如图记录了学生学习某概念时t与s的三组数据,根据上述函数模型和数据,可推断出当学生接受能力最强时,提出概念的时间为( )
A.8min B.13min C.20min D.25min
9.在平面直角坐标系中,点的坐标,点的坐标为为实数),当长取得最小值时,的值为( )
A. B. C. D.
10.一次函数y=kx+b的图象与反比例函数的图象交于A(2,1),B(,n)两点,则n﹣k的值为( )
A.2 B.﹣2 C.6 D.﹣6
二、填空题
11.如图,在中,,若,则_____.
12.某水果店销售一批水果,平均每天可售出,每千克盈利元,经调查发现,每千克降价元,商店平均每天可多售出水果,则商店平均每天的最高利润为______________ 元
13.如图,在轴上方,平行于轴的直线与反比例函数和的图象分别交于两点,连接.若的面积为则 __________.
14.已知二次函数为常数),当时,的最大值是,则的值是__________.
15.已知,则=_____.
16.如图,函数y=和y=﹣的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为_____.
三、解答题
17.抛物线的顶点为,它的形状与相同,但开口方向与之相反.
(1)直接写出抛物线的解析式 ;
(2)求抛物线与轴的交点坐标.
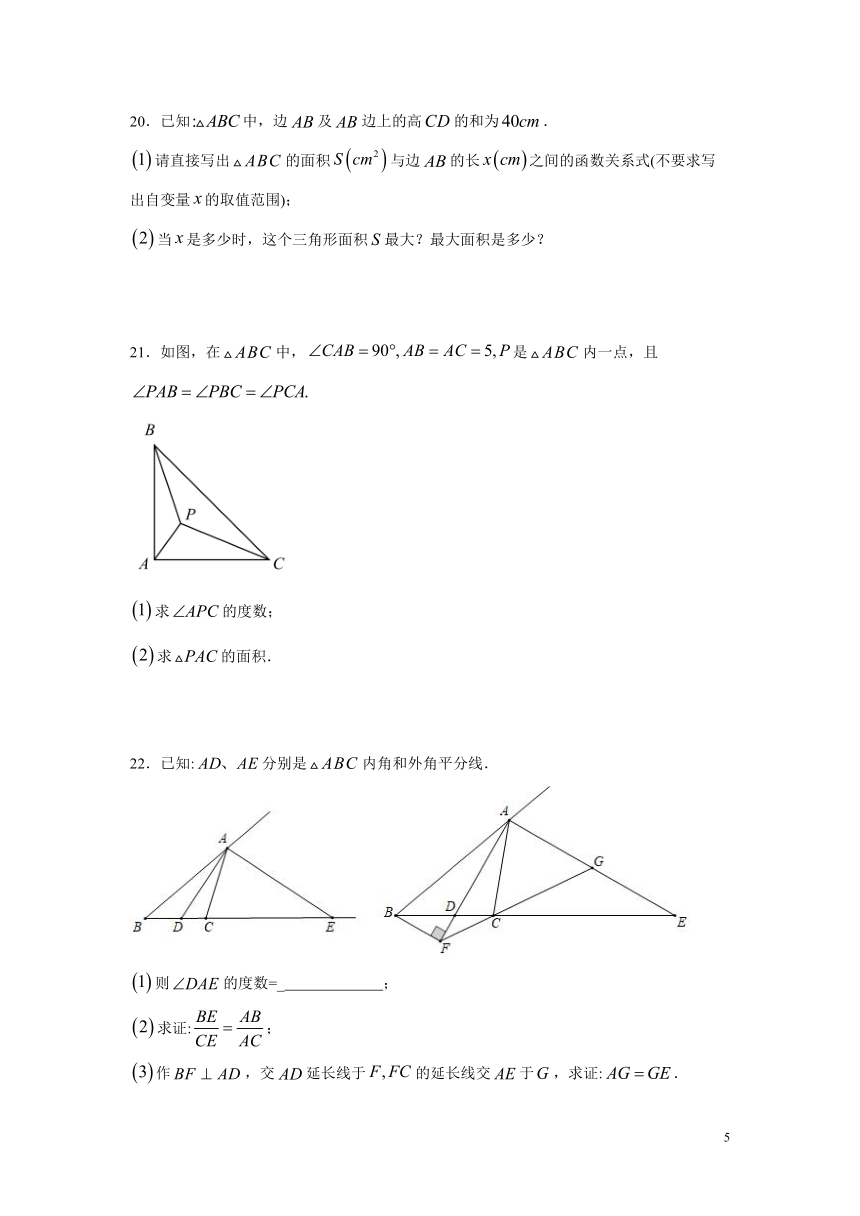
18.如图,正方形对角线的交点在平面直角坐标系的原点,且边与坐标轴平行或垂直,AB=4.
(1)如果反比例函数的图象经过点,求这个反比例函数的表达式;
(2)如果反比例函数的图象与正方形有公共点,请直接写出的取值范围.
19.如图,在中,分别是边上的点,连接,且,.
求证:;
如果是的中点,求的长,
20.已知中,边及边上的高的和为.
请直接写出的面积与边的长之间的函数关系式(不要求写出自变量的取值范围);
当是多少时,这个三角形面积最大?最大面积是多少?
21.如图,在中,是内一点,且
求的度数;
求的面积.
22.已知:分别是内角和外角平分线.
则的度数=_ ;
求证:;
作,交延长线于的延长线交于,求证:.
23.定义: 在平面直角坐标系中,如果点和都在某函数的图象上,则称点是图象的一对“相关点”.例如,点和点是直线的一对相关点.
请写出反比例函数的图象上的一对相关点的坐标;
如图,抛物线的对称轴为直线,与轴交于点.
求抛物线的解析式:
若点是抛物线上的一对相关点,直线与轴交于点,点为抛物线上之间的一点,求面积的最大值.
24.如图,两个反比例函数y=和y=在第一象限内的图象分别是C1和C2,设点P(1,4)在C1上,PA⊥x轴于点A,交C2于点B(1,m),求k,m的值及△POB的面积.
25.如图,△ABC∽△ADE,AB=30 cm,BD=18 cm,BC=20 cm,∠BAC=75°,∠ABC=40°.
(1)求∠AED的度数.
(2)求DE的长.
参考答案
1.C
【分析】
根据顶点式y=a(x-h)2+k的对称轴是直线x=h,找出h即可得出答案.
【详解】
解:二次函数y=x2的对称轴为y轴.
故选:C .
【点睛】
本题考查二次函数的性质,解题关键是顶点式y=a(x-h)2+k的对称轴是直线x=h,顶点坐标为(h,k).
2.D
【详解】
∵,
∴==,
故选D
3.D
【解析】
试题解析:∵a=1>0,
∴二次函数y=(x-1)2-3有最小值-3.
故选D.
考点:二次函数的最值.
4.B
【解析】
【分析】
直接根据二次函数图象平移的法则即可得出结论.
【详解】
解:根据“上加下减,左加右减”的法则可知,将抛物线向右平移2个单位,再向下平移1个单位所得抛物线的表达式是-1.
所以平移后抛物线的顶点坐标是(2,-1).
【点睛】
本题考查的是二次函数的图象与几何变换,熟知“上加下减,左加右减”的法则是解答此题的关键.
5.C
【分析】
根据相似三角形的性质与判定即可求出答案.
【详解】
解:∵DE∥BC,
∴△ABC∽△ADE,
∴,
∴,
∴AC=3.6,
故选:C.
【点睛】
本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于基础题型.
6.D
【分析】
分别把A、B点的坐标代入y=ax2得a的值,根据二次函数的性质得到a的取值范围.
【详解】
解:把A(1,1)代入y=ax2得a=1,
把B(3,1)代入y=ax2得a=,
所以a的取值范围为.
故选D.
【点睛】
本题考查了二次函数图象与系数的关系:二次项系数a决定抛物线的开口方向和大小.
7.C
【分析】
易证△DEF∽△DAB,△BEF∽△BCD,根据相似三角形的性质可得= ,=,从而可得+=+=1.然后把AB=1,CD=3代入即可求出EF的值.
【详解】
∵AB、CD、EF都与BD垂直,
∴AB∥CD∥EF,
∴△DEF∽△DAB,△BEF∽△BCD,
∴= ,=,
∴+=+==1.
∵AB=1,CD=3,
∴+=1,
∴EF=.
故选C.
【点睛】
本题考查了相似三角形的判定及性质定理,熟练掌握性质定理是解题的关键.
8.B
【分析】
先利用条件求出解析式,再变式求出最值即可解答.
【详解】
解:已知满足函数关系s=at2+bt+c(a≠0),
根据图像可知经过(0,43),(20,55),(30,31),
将已知点代入解析式得s=-0.1+2.6t+43,
根据函数性质得t=-=13时,s最大,
故选B.
【点睛】
本题主要考察求函数最值,可利用配方法,公式法等.
9.A
【分析】
由两点间的距离公式可得出PQ2关于t的二次函数关系式,利用配方法结合二次函数的性质即可得出当PQ取最小值时t的值.
【详解】
解:由两点间的距离公式可知:PQ2=(t-1)2+(t--2)2=(t+)2+16,
∵>0,
∴当t=时,PQ2最小.
故选:A.
【点睛】
本题考查了两点间的距离公式以及二次函数的性质,解题的关键是找出PQ2关于t的二次函数关系式.
10.C
【分析】
把A的坐标代入反比例函数的解析式即可求出反比例函数的解析式,把B的坐标代入求出n的值,把A、B的坐标代入一次函数y=kx+b即可求出k的值.
【详解】
解:∵把A(2,1)代入y= 得:m=2,
∴反比例函数的解析式是y=,
∵B(,n)代入反比例函数y=得:n=4,
∴B的坐标是(,4),
把A、B的坐标代入一次函数y1=kx+b,得,
解得:k=﹣2,
∴n﹣k=4+2=6,
故选:C.
【点睛】
本题是一次函数和反比例函数的综合题,解答关键是应用待定系数法确定函数关系式.
11.
【分析】
由,可知:,列出比例式,即可得到答案.
【详解】
∵,
∴,
∴,
∵,
∴,
选答案是:.
【点睛】
本题主要考查相似三角形的判定和性质定理,根据相似三角形的性质,列出比例式是解题的关键.
12.
【分析】
设每千克降价x元,先用含x的式子表示出每天的销售量,再设商店平均每天的利润为w元,根据每千克的盈利乘以销售量等于利润,写出关于x的函数,写成顶点式,根据二次函数的性质,可得答案.
【详解】
解:设每千克降价x元,由题意得每天的销售量为:
40+×10=(40+20x)千克,
设商店平均每天的利润为w元,由题意得:
w=(4-x)(40+20x)
=-20x2+40x+160
=-20(x-1)2+180,
∵二次项系数为-20<0,
∴当x=1时,w取得最大值180元.
故答案为:180.
【点睛】
本题考查了二次函数在销售问题中的应用,理清题中的数量关系,正确列出函数关系式并明确二次函数的相关性质,是解题的关键.
13.
【分析】
根据AB∥x轴,设A(x,),B(,),得到AB=-x,根据△AOB的面积为6,列方程即可得到结论.
【详解】
解:∵AB∥x轴,
∴设A(x,),B(,),
∴AB=-x,
∵△AOB的面积为6,
∴(-x)×=6,
∴k2-k1=12,
故答案为:12.
【点睛】
本题考查的是反比例函数的性质以及反比例函数图像上的点,解题的关键是将A和B的坐标表示出来,从而得到△AOB的面积的代数式.
14.和
【分析】
根据题目中的函数解析式和当-2≤x≤4时,y的最大值是15,利用分类讨论的方法可以求得m的值,本题得以解决.
【详解】
解:二次函数y=-x2+mx+m=-(x-)2++m,
当4<时,即m>8,
在-2≤x≤4时,x=4时取得最大值,则15=-42+4m+m,得m=6.2(舍去);
当<-2时,即m<-4,
在-2≤x≤4时,x=-2时取得最大值,则15=-22-2m+m,得m=-19,
当-2≤≤4时,即-4≤m≤8,
在-2≤x≤4时,x=时取得最大值,则15=+m,得m1=6,m2=-10(舍去),
由上可得,m的值是和,
故答案为:和.
【点睛】
本题考查考查二次函数的性质、二次函数的最值,解答本题的关键是明确题意,利用二次函数的性质和分类讨论的方法解答.
15.
【分析】
设,然后表示出a,b,c,再进行化简即可.
【详解】
解:设.
则根据比例的性质,得a=2k,b=3k,c=4k,
∴==;
故答案为:.
【点睛】
本题考查了比例的性质,熟练掌握设k法是解题的关键.
16.8
【详解】
解:∵点P在y=上,
∴|xp|×|yp|=|k|=1,
∴设P的坐标是(a,)(a为正数),
∵PA⊥x轴,
∴A的横坐标是a,
∵A在y=﹣上,
∴A的坐标是(a,﹣),
∵PB⊥y轴,
∴B的纵坐标是,
∵B在y=﹣上,
∴代入得: =﹣,
解得:x=﹣3a,
∴B的坐标是(﹣3a,),
∴PA=|﹣(﹣)|=,PB=|a﹣(﹣3a)|=4a,
∵PA⊥x轴,PB⊥y轴,x轴⊥y轴,
∴PA⊥PB,
∴△PAB的面积是:PA×PB=××4a=8.
故答案为8.
【点睛】
本题考查了反比例函数和三角形面积公式的应用,关键是能根据P点的坐标得出A、B的坐标,本题具有一定的代表性,是一道比较好的题目.
17.(1);(2)
【分析】
(1)由抛物线y=a(x+h)2的顶点为(-2,0),得出h=2,抛物线y=a(x+h)2的形状与y=3x2的相同,开口方向相反,得出a=-3,从而确定该抛物线的函数表达式;
(2)根据图象上点的坐标特征求得即可.
【详解】
解:(1)∵抛物线y=a(x+h)2的顶点为(-2,0),
∴-h=-2,
∴h=2,
抛物线y=a(x+h)2的形状与y=3x2的相同,开口方向相反,
∴a=-3,
则该抛物线的函数表达式是y=-3(x+2)2;
(2)当时,,
抛物线与轴的交点坐标为.
【点睛】
主要考查了待定系数法求二次函数的解析式.要求掌握二次函数图象的性质,并会利用性质得出系数之间的数量关系进行解题.
18.(1);(2) 或
【分析】
(1)根据题意得出A的坐标,然后根据待定系数法即可求得;
(2)根据A、B、C、D的坐标,结合图象即可求得.
【详解】
解:(1)由题意,得,
反比例函数的图象经过点,
,
反比例函数的表达式;
(2)由图象可知:
当反比例函数刚好经过A和C,或B和D时,k分别为4和-4,k≠0,
则如果反比例函数的图象与正方形ABCD有公共点,
k的取值范围是或.
【点睛】
本题考查了待定系数法求反比例函数的解析式,正方形的性质以及反比例函数的图象,根据图象得出正方形各点的坐标是解题的关键.
19.(1)见解析;(2)
【分析】
(1)由条件得出,根据相似三角形的判定即可求出证.
(2)由于点E是AC的中点,设AE=x,根据相似三角形的性质可知,从而列出方程解出x的值.
【详解】
解:(1)证明:
,
,
,
,
;
(2)由(1)知,
,
点是的中点,设,
,
,
,
解得(负值舍去) .
.
【点睛】
本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定.
20.(1);(2)当为时,三角形面积最大,最大面积是
【分析】
(1)S=x×这边上的高,把相关数值代入化简即可;
(2)结合(1)得到的关系式,利用公式法求得二次函数的最值即可.
【详解】
解:(1)由题意可得:;
(2),
有最大值,
当==20时,有最大值为,
∴当为时,三角形面积最大,最大面积是.
【点睛】
本题考查二次函数的应用,掌握二次函数的最值求法是解决本题的关键.
21.(1)90°;(2)5
【分析】
(1)根据,利用余角的性质求解;
(2)证明,得到,设PA为x,将相应边表示出来,根据AC=5求出x,即可计算△PAC的面积.
【详解】
解:(1),
;
(2)在等腰直角中,
,
,
∴,
∴,
设,
,则,
,
,
.
【点睛】
本题考查了相似三角形的判定和性质,等腰直角三角形的性质,解题的关键是正确寻找相似三角形,证明∠APC=90°是本题的突破点,属于中考常考题型.
22.(1)90°;(2)见解析;(3)见解析
【分析】
(1)根据角平分线的定义和邻补角的定义即可解得;
(2)过点C作CN∥AB交AE于点N,如图,易证CA=CN.由CN∥AB可得△ECN∽△EBA,则有,由CA=CN可得;
(3)分别延长BF、AC交于点H,证明△ABF≌△AHF,可得BF=HF,证明△BCF∽△ECG,△ACG∽△HCF,可得比例线段,则结论得证.
【详解】
解:(1)∵AD、AE分别是△ABC中∠A内角的平分线和外角平分线,
∴∠DAE=∠DAC+∠EAC
=∠BAC+∠CAF
=(∠BAC+∠CAF)
=×180°=90°.
故答案为:90°;
(2)证明:过点作交于点,如图1,
则有.
,
,
.
,
,
,
;
(3)如图2,分别延长、交于点;
为的角平分线,
;
在与中,
,
,
;
,,
,
,,
,,
,
∵,
.
【点睛】
本题主要考查了相似三角形的判定与性质、全等三角形的判定与性质、等腰三角形的判定、角平分线的定义等知识,添加平行线构造相似三角形是解题的关键.
23.(1),;(2)①;②
【分析】
(1)xy=6,当x=2时,y=3,当x=3时,y=2,即可求解;
(2)①根据C(0,-1)求得c,根据x=-1,函数对称轴为:x=-=-1,解得:b=-2,即可求解;
②由“相关点”的定义,可得直线MN的表达式,求出点M、N的坐标,将△PMN面积利用S=×PQ×(xM-xN)表示出来即可求解.
【详解】
解:(1)xy=6,当x=2时,y=3,当x=3时,y=2,
故答案为:(2,3)和(3,2);
(2)①∵抛物线的对称轴为直线,
解得,
抛物线与轴交于点,
,
抛物线的解析式为;
②由相关点定义得,点关于直线对称.
又直线与轴交于点,
直线的解析式为.
代入抛物线的解析式中,并整理,得
,
解得,,
两点坐标为和.
设点的横坐标为,则点,
过作轴交直线于点,
则点坐标为,
,
即当时,的面积最大,最大值为.
【点睛】
本题考查的是二次函数综合运用,涉及到一次函数、图形的面积计算等,这种新定义类的题目,通常按照题设的顺序逐次求解较为容易.
24.k=4,m=2,.
【详解】
试题分析:将点P的坐标代入C1的解析式即可求出k的值;将点B的横坐标代入C2的解析式即可求出m的值;S△POB=S△POA-S△BOA,由反比例函数k的几何意义可以分别求出S△POA、S△BOA的值.
试题解析:
∵P(1,4),∴k=4;
∵B(1,m),C2解析式为:y=,∴m=2;
S△POB=S△POA-S△BOA=2-1=1.
点睛:掌握反比例函数k的几何意义.
25.(1)65°(2)8
【详解】
试题分析:(1)∵
∴
∵△ABC∽△ADE
∴
(2) ∵
∴
又∵△ABC∽△ADE
∴ 即:
∴.
【点睛】
本题考查相似三角形,掌握相似三角形的性质是解本题的关键,所以要求考生对相似三角形的性质要熟悉.
(
2
)
(
1
)
一、选择题。(每小题只有一个正确答案)
1.二次函数的对称轴是
A.直线 B.直线 C.y轴 D.x轴
2.若,则的值为( )
A.1 B. C. D.
3.已知二次函数y=(x-1)2-3,则此二次函数( )
A.有最大值1 B.有最小值1
C.有最大值-3 D.有最小值-3
4.将抛物线向右平移2个单位,再向下平移1个单位,则平移后抛物线的顶点坐标是( )
A.(2,1) B.(2,-1) C.(-2,-1) D.(-2,1)
5.如图,线段相交于点.若,则的长为( )
A. B. C. D.
6.如图,在平面直角坐标系中有两点,如果抛物线与线段有公共点,那么的取值范围是( )
A. B. C. D.
7.如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
A. B. C. D.
8.心理学家发现:课堂上,学生对概念的接受能力s与提出概念的时间t(单位:min)之间近似满足函数关系s=at2+bt+c(a≠0),s值越大,表示接受能力越强.如图记录了学生学习某概念时t与s的三组数据,根据上述函数模型和数据,可推断出当学生接受能力最强时,提出概念的时间为( )
A.8min B.13min C.20min D.25min
9.在平面直角坐标系中,点的坐标,点的坐标为为实数),当长取得最小值时,的值为( )
A. B. C. D.
10.一次函数y=kx+b的图象与反比例函数的图象交于A(2,1),B(,n)两点,则n﹣k的值为( )
A.2 B.﹣2 C.6 D.﹣6
二、填空题
11.如图,在中,,若,则_____.
12.某水果店销售一批水果,平均每天可售出,每千克盈利元,经调查发现,每千克降价元,商店平均每天可多售出水果,则商店平均每天的最高利润为______________ 元
13.如图,在轴上方,平行于轴的直线与反比例函数和的图象分别交于两点,连接.若的面积为则 __________.
14.已知二次函数为常数),当时,的最大值是,则的值是__________.
15.已知,则=_____.
16.如图,函数y=和y=﹣的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为_____.
三、解答题
17.抛物线的顶点为,它的形状与相同,但开口方向与之相反.
(1)直接写出抛物线的解析式 ;
(2)求抛物线与轴的交点坐标.
18.如图,正方形对角线的交点在平面直角坐标系的原点,且边与坐标轴平行或垂直,AB=4.
(1)如果反比例函数的图象经过点,求这个反比例函数的表达式;
(2)如果反比例函数的图象与正方形有公共点,请直接写出的取值范围.
19.如图,在中,分别是边上的点,连接,且,.
求证:;
如果是的中点,求的长,
20.已知中,边及边上的高的和为.
请直接写出的面积与边的长之间的函数关系式(不要求写出自变量的取值范围);
当是多少时,这个三角形面积最大?最大面积是多少?
21.如图,在中,是内一点,且
求的度数;
求的面积.
22.已知:分别是内角和外角平分线.
则的度数=_ ;
求证:;
作,交延长线于的延长线交于,求证:.
23.定义: 在平面直角坐标系中,如果点和都在某函数的图象上,则称点是图象的一对“相关点”.例如,点和点是直线的一对相关点.
请写出反比例函数的图象上的一对相关点的坐标;
如图,抛物线的对称轴为直线,与轴交于点.
求抛物线的解析式:
若点是抛物线上的一对相关点,直线与轴交于点,点为抛物线上之间的一点,求面积的最大值.
24.如图,两个反比例函数y=和y=在第一象限内的图象分别是C1和C2,设点P(1,4)在C1上,PA⊥x轴于点A,交C2于点B(1,m),求k,m的值及△POB的面积.
25.如图,△ABC∽△ADE,AB=30 cm,BD=18 cm,BC=20 cm,∠BAC=75°,∠ABC=40°.
(1)求∠AED的度数.
(2)求DE的长.
参考答案
1.C
【分析】
根据顶点式y=a(x-h)2+k的对称轴是直线x=h,找出h即可得出答案.
【详解】
解:二次函数y=x2的对称轴为y轴.
故选:C .
【点睛】
本题考查二次函数的性质,解题关键是顶点式y=a(x-h)2+k的对称轴是直线x=h,顶点坐标为(h,k).
2.D
【详解】
∵,
∴==,
故选D
3.D
【解析】
试题解析:∵a=1>0,
∴二次函数y=(x-1)2-3有最小值-3.
故选D.
考点:二次函数的最值.
4.B
【解析】
【分析】
直接根据二次函数图象平移的法则即可得出结论.
【详解】
解:根据“上加下减,左加右减”的法则可知,将抛物线向右平移2个单位,再向下平移1个单位所得抛物线的表达式是-1.
所以平移后抛物线的顶点坐标是(2,-1).
【点睛】
本题考查的是二次函数的图象与几何变换,熟知“上加下减,左加右减”的法则是解答此题的关键.
5.C
【分析】
根据相似三角形的性质与判定即可求出答案.
【详解】
解:∵DE∥BC,
∴△ABC∽△ADE,
∴,
∴,
∴AC=3.6,
故选:C.
【点睛】
本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于基础题型.
6.D
【分析】
分别把A、B点的坐标代入y=ax2得a的值,根据二次函数的性质得到a的取值范围.
【详解】
解:把A(1,1)代入y=ax2得a=1,
把B(3,1)代入y=ax2得a=,
所以a的取值范围为.
故选D.
【点睛】
本题考查了二次函数图象与系数的关系:二次项系数a决定抛物线的开口方向和大小.
7.C
【分析】
易证△DEF∽△DAB,△BEF∽△BCD,根据相似三角形的性质可得= ,=,从而可得+=+=1.然后把AB=1,CD=3代入即可求出EF的值.
【详解】
∵AB、CD、EF都与BD垂直,
∴AB∥CD∥EF,
∴△DEF∽△DAB,△BEF∽△BCD,
∴= ,=,
∴+=+==1.
∵AB=1,CD=3,
∴+=1,
∴EF=.
故选C.
【点睛】
本题考查了相似三角形的判定及性质定理,熟练掌握性质定理是解题的关键.
8.B
【分析】
先利用条件求出解析式,再变式求出最值即可解答.
【详解】
解:已知满足函数关系s=at2+bt+c(a≠0),
根据图像可知经过(0,43),(20,55),(30,31),
将已知点代入解析式得s=-0.1+2.6t+43,
根据函数性质得t=-=13时,s最大,
故选B.
【点睛】
本题主要考察求函数最值,可利用配方法,公式法等.
9.A
【分析】
由两点间的距离公式可得出PQ2关于t的二次函数关系式,利用配方法结合二次函数的性质即可得出当PQ取最小值时t的值.
【详解】
解:由两点间的距离公式可知:PQ2=(t-1)2+(t--2)2=(t+)2+16,
∵>0,
∴当t=时,PQ2最小.
故选:A.
【点睛】
本题考查了两点间的距离公式以及二次函数的性质,解题的关键是找出PQ2关于t的二次函数关系式.
10.C
【分析】
把A的坐标代入反比例函数的解析式即可求出反比例函数的解析式,把B的坐标代入求出n的值,把A、B的坐标代入一次函数y=kx+b即可求出k的值.
【详解】
解:∵把A(2,1)代入y= 得:m=2,
∴反比例函数的解析式是y=,
∵B(,n)代入反比例函数y=得:n=4,
∴B的坐标是(,4),
把A、B的坐标代入一次函数y1=kx+b,得,
解得:k=﹣2,
∴n﹣k=4+2=6,
故选:C.
【点睛】
本题是一次函数和反比例函数的综合题,解答关键是应用待定系数法确定函数关系式.
11.
【分析】
由,可知:,列出比例式,即可得到答案.
【详解】
∵,
∴,
∴,
∵,
∴,
选答案是:.
【点睛】
本题主要考查相似三角形的判定和性质定理,根据相似三角形的性质,列出比例式是解题的关键.
12.
【分析】
设每千克降价x元,先用含x的式子表示出每天的销售量,再设商店平均每天的利润为w元,根据每千克的盈利乘以销售量等于利润,写出关于x的函数,写成顶点式,根据二次函数的性质,可得答案.
【详解】
解:设每千克降价x元,由题意得每天的销售量为:
40+×10=(40+20x)千克,
设商店平均每天的利润为w元,由题意得:
w=(4-x)(40+20x)
=-20x2+40x+160
=-20(x-1)2+180,
∵二次项系数为-20<0,
∴当x=1时,w取得最大值180元.
故答案为:180.
【点睛】
本题考查了二次函数在销售问题中的应用,理清题中的数量关系,正确列出函数关系式并明确二次函数的相关性质,是解题的关键.
13.
【分析】
根据AB∥x轴,设A(x,),B(,),得到AB=-x,根据△AOB的面积为6,列方程即可得到结论.
【详解】
解:∵AB∥x轴,
∴设A(x,),B(,),
∴AB=-x,
∵△AOB的面积为6,
∴(-x)×=6,
∴k2-k1=12,
故答案为:12.
【点睛】
本题考查的是反比例函数的性质以及反比例函数图像上的点,解题的关键是将A和B的坐标表示出来,从而得到△AOB的面积的代数式.
14.和
【分析】
根据题目中的函数解析式和当-2≤x≤4时,y的最大值是15,利用分类讨论的方法可以求得m的值,本题得以解决.
【详解】
解:二次函数y=-x2+mx+m=-(x-)2++m,
当4<时,即m>8,
在-2≤x≤4时,x=4时取得最大值,则15=-42+4m+m,得m=6.2(舍去);
当<-2时,即m<-4,
在-2≤x≤4时,x=-2时取得最大值,则15=-22-2m+m,得m=-19,
当-2≤≤4时,即-4≤m≤8,
在-2≤x≤4时,x=时取得最大值,则15=+m,得m1=6,m2=-10(舍去),
由上可得,m的值是和,
故答案为:和.
【点睛】
本题考查考查二次函数的性质、二次函数的最值,解答本题的关键是明确题意,利用二次函数的性质和分类讨论的方法解答.
15.
【分析】
设,然后表示出a,b,c,再进行化简即可.
【详解】
解:设.
则根据比例的性质,得a=2k,b=3k,c=4k,
∴==;
故答案为:.
【点睛】
本题考查了比例的性质,熟练掌握设k法是解题的关键.
16.8
【详解】
解:∵点P在y=上,
∴|xp|×|yp|=|k|=1,
∴设P的坐标是(a,)(a为正数),
∵PA⊥x轴,
∴A的横坐标是a,
∵A在y=﹣上,
∴A的坐标是(a,﹣),
∵PB⊥y轴,
∴B的纵坐标是,
∵B在y=﹣上,
∴代入得: =﹣,
解得:x=﹣3a,
∴B的坐标是(﹣3a,),
∴PA=|﹣(﹣)|=,PB=|a﹣(﹣3a)|=4a,
∵PA⊥x轴,PB⊥y轴,x轴⊥y轴,
∴PA⊥PB,
∴△PAB的面积是:PA×PB=××4a=8.
故答案为8.
【点睛】
本题考查了反比例函数和三角形面积公式的应用,关键是能根据P点的坐标得出A、B的坐标,本题具有一定的代表性,是一道比较好的题目.
17.(1);(2)
【分析】
(1)由抛物线y=a(x+h)2的顶点为(-2,0),得出h=2,抛物线y=a(x+h)2的形状与y=3x2的相同,开口方向相反,得出a=-3,从而确定该抛物线的函数表达式;
(2)根据图象上点的坐标特征求得即可.
【详解】
解:(1)∵抛物线y=a(x+h)2的顶点为(-2,0),
∴-h=-2,
∴h=2,
抛物线y=a(x+h)2的形状与y=3x2的相同,开口方向相反,
∴a=-3,
则该抛物线的函数表达式是y=-3(x+2)2;
(2)当时,,
抛物线与轴的交点坐标为.
【点睛】
主要考查了待定系数法求二次函数的解析式.要求掌握二次函数图象的性质,并会利用性质得出系数之间的数量关系进行解题.
18.(1);(2) 或
【分析】
(1)根据题意得出A的坐标,然后根据待定系数法即可求得;
(2)根据A、B、C、D的坐标,结合图象即可求得.
【详解】
解:(1)由题意,得,
反比例函数的图象经过点,
,
反比例函数的表达式;
(2)由图象可知:
当反比例函数刚好经过A和C,或B和D时,k分别为4和-4,k≠0,
则如果反比例函数的图象与正方形ABCD有公共点,
k的取值范围是或.
【点睛】
本题考查了待定系数法求反比例函数的解析式,正方形的性质以及反比例函数的图象,根据图象得出正方形各点的坐标是解题的关键.
19.(1)见解析;(2)
【分析】
(1)由条件得出,根据相似三角形的判定即可求出证.
(2)由于点E是AC的中点,设AE=x,根据相似三角形的性质可知,从而列出方程解出x的值.
【详解】
解:(1)证明:
,
,
,
,
;
(2)由(1)知,
,
点是的中点,设,
,
,
,
解得(负值舍去) .
.
【点睛】
本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定.
20.(1);(2)当为时,三角形面积最大,最大面积是
【分析】
(1)S=x×这边上的高,把相关数值代入化简即可;
(2)结合(1)得到的关系式,利用公式法求得二次函数的最值即可.
【详解】
解:(1)由题意可得:;
(2),
有最大值,
当==20时,有最大值为,
∴当为时,三角形面积最大,最大面积是.
【点睛】
本题考查二次函数的应用,掌握二次函数的最值求法是解决本题的关键.
21.(1)90°;(2)5
【分析】
(1)根据,利用余角的性质求解;
(2)证明,得到,设PA为x,将相应边表示出来,根据AC=5求出x,即可计算△PAC的面积.
【详解】
解:(1),
;
(2)在等腰直角中,
,
,
∴,
∴,
设,
,则,
,
,
.
【点睛】
本题考查了相似三角形的判定和性质,等腰直角三角形的性质,解题的关键是正确寻找相似三角形,证明∠APC=90°是本题的突破点,属于中考常考题型.
22.(1)90°;(2)见解析;(3)见解析
【分析】
(1)根据角平分线的定义和邻补角的定义即可解得;
(2)过点C作CN∥AB交AE于点N,如图,易证CA=CN.由CN∥AB可得△ECN∽△EBA,则有,由CA=CN可得;
(3)分别延长BF、AC交于点H,证明△ABF≌△AHF,可得BF=HF,证明△BCF∽△ECG,△ACG∽△HCF,可得比例线段,则结论得证.
【详解】
解:(1)∵AD、AE分别是△ABC中∠A内角的平分线和外角平分线,
∴∠DAE=∠DAC+∠EAC
=∠BAC+∠CAF
=(∠BAC+∠CAF)
=×180°=90°.
故答案为:90°;
(2)证明:过点作交于点,如图1,
则有.
,
,
.
,
,
,
;
(3)如图2,分别延长、交于点;
为的角平分线,
;
在与中,
,
,
;
,,
,
,,
,,
,
∵,
.
【点睛】
本题主要考查了相似三角形的判定与性质、全等三角形的判定与性质、等腰三角形的判定、角平分线的定义等知识,添加平行线构造相似三角形是解题的关键.
23.(1),;(2)①;②
【分析】
(1)xy=6,当x=2时,y=3,当x=3时,y=2,即可求解;
(2)①根据C(0,-1)求得c,根据x=-1,函数对称轴为:x=-=-1,解得:b=-2,即可求解;
②由“相关点”的定义,可得直线MN的表达式,求出点M、N的坐标,将△PMN面积利用S=×PQ×(xM-xN)表示出来即可求解.
【详解】
解:(1)xy=6,当x=2时,y=3,当x=3时,y=2,
故答案为:(2,3)和(3,2);
(2)①∵抛物线的对称轴为直线,
解得,
抛物线与轴交于点,
,
抛物线的解析式为;
②由相关点定义得,点关于直线对称.
又直线与轴交于点,
直线的解析式为.
代入抛物线的解析式中,并整理,得
,
解得,,
两点坐标为和.
设点的横坐标为,则点,
过作轴交直线于点,
则点坐标为,
,
即当时,的面积最大,最大值为.
【点睛】
本题考查的是二次函数综合运用,涉及到一次函数、图形的面积计算等,这种新定义类的题目,通常按照题设的顺序逐次求解较为容易.
24.k=4,m=2,.
【详解】
试题分析:将点P的坐标代入C1的解析式即可求出k的值;将点B的横坐标代入C2的解析式即可求出m的值;S△POB=S△POA-S△BOA,由反比例函数k的几何意义可以分别求出S△POA、S△BOA的值.
试题解析:
∵P(1,4),∴k=4;
∵B(1,m),C2解析式为:y=,∴m=2;
S△POB=S△POA-S△BOA=2-1=1.
点睛:掌握反比例函数k的几何意义.
25.(1)65°(2)8
【详解】
试题分析:(1)∵
∴
∵△ABC∽△ADE
∴
(2) ∵
∴
又∵△ABC∽△ADE
∴ 即:
∴.
【点睛】
本题考查相似三角形,掌握相似三角形的性质是解本题的关键,所以要求考生对相似三角形的性质要熟悉.
(
2
)
(
1
)
同课章节目录
