7.1.2三角形的高、中线和角平分线[下学期]
文档属性
| 名称 | 7.1.2三角形的高、中线和角平分线[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-30 00:00:00 | ||
图片预览




文档简介
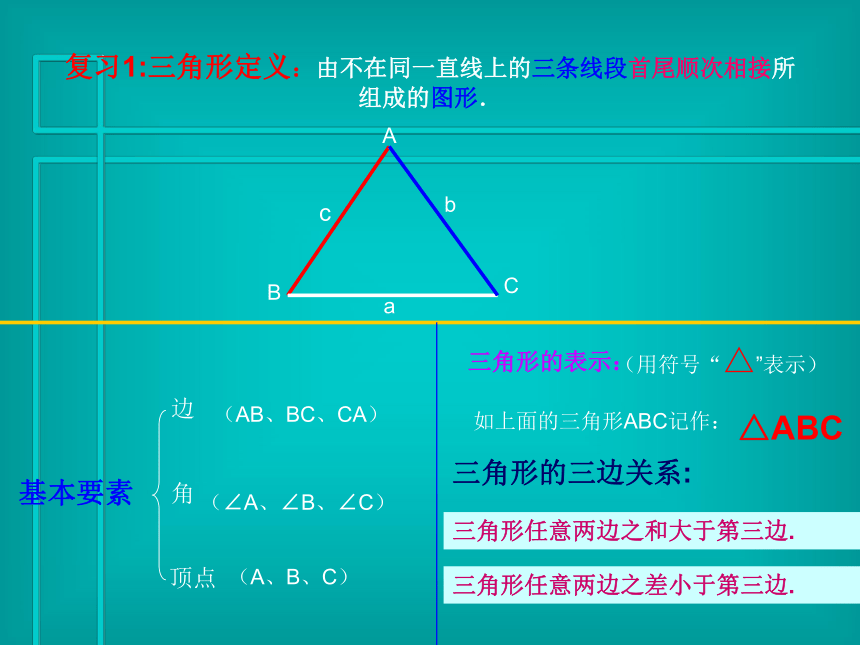
课件12张PPT。七年级下册第七章授课教师:许海健复习1:三角形定义:由不在同一直线上的三条线段首尾顺次相接所组成的图形.边基本要素角顶点ABC(AB、BC、CA)(∠A、∠B、∠C)(A、B、C)如上面的三角形ABC记作:三角形的表示:(用符号“△”表示)△ABCbca三角形的三边关系:三角形任意两边之和大于第三边.三角形任意两边之差小于第三边.复习2:
1、现有长度为2cm、3cm、4cm、5cm的木棒,从中任取三根,能组成三角形的个数为( )
A、1个 B、2个 C、3个 D、4个
2、如果一个三角形两边为2cm,7cm,且第三边为奇数,则第三边的长为 cm。
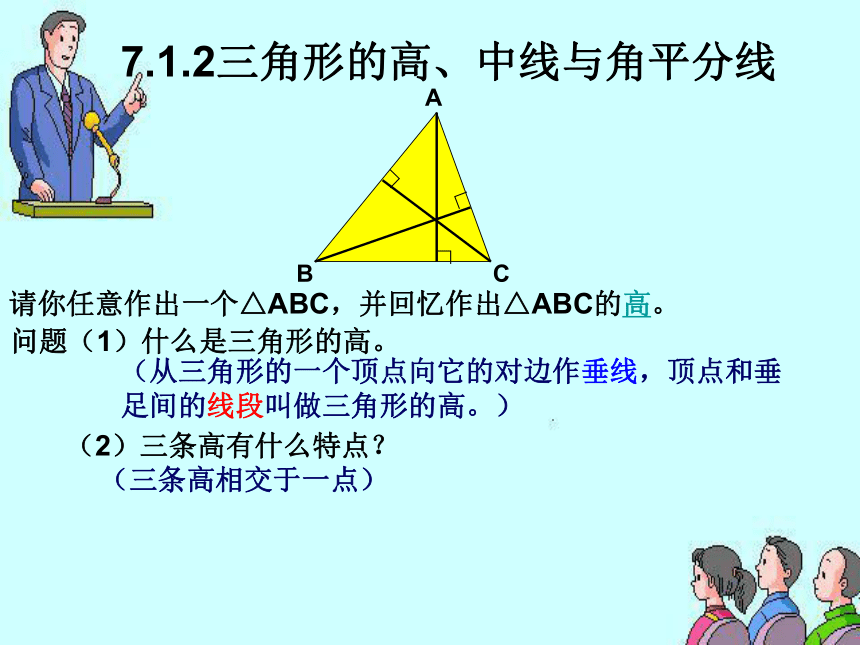
3、若等腰三角形的两边长为4,6,则等腰三角形周长为 。 C714或16请你任意作出一个△ABC,并回忆作出△ABC的高。 (2)三条高有什么特点?问题(1)什么是三角形的高。(从三角形的一个顶点向它的对边作垂线,顶点和垂足间的线段叫做三角形的高。)(三条高相交于一点)7.1.2三角形的高、中线与角平分线∟∟∟(3)你能用折纸的方法找出你准备好的三角形的三条高吗? (4)高的交点有何特别之处?(锐角三角形的高的交点在三角形内,直角三角形的高的交点是两直角边的交点,钝角三角形的高的交点在三角形外)请拿出你准备好的三角形纸片,在上面定义三个顶点分别为A、B、C,对折,使AC与AB所在直线重合,折痕与BC交于点D。请拿出你准备好的三角形纸片,在上面定义三个顶点分别为A、B、C,把B、C重合对折,折痕与BC交于点D。(演示)问题:(1)D点有什么特殊性?(2)连接线段AD,AD把△ABC分成的两个三角形的面积有何关系?(3)请归纳线段AD的特点。 (4)用语言描述中线定义。 (点D是线段AB的中点)(两个三角形的面积相等)(在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线)问题:(1)通过这个操作你认为AD有什么位置特点?(2)你能用尺规作出AD吗?(3)请给出三角形角平分线的定义。(把∠A分成两个相等的角)(三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。)演示(1)你认为一个三角形有几条高,几条中线,几条角平分线?并分别作出来。(3)你认为“三线”定义中,高与线段垂线、三角形角平分线与角的平分线、中线与线段中点有何异同?(2)通过本组作出的三线,请说明它们各自的共性。巩固新知:(都有三条)(都相交于一点)(三角形的高、角平分线、中线都是线段)练习:②AE是△ABC中线,那么BE= = BC。 ③如下图,在△ABC中∠BAC=60o,∠B=45o,AD是∠BAC的角平分线,求∠ADB的度数。∠CAD∠BACCE答案:∠ADB=1050解决问题㈠如右图,D、E分别为△ABC的边AC、BC的中点,下列说法正确吗?
(1)DE是△BDC的中线。
(2)BD是△ABC的中线。
(3)AD=CD,BE=EC。
总结归纳请同学们回忆一下本课主要内容,并谈谈你有什么收获? 三线高(线)中线角平分线都是由三角形的一个顶点到对边(或对边延长线)上的点连结的线段作业教科书75页习题7.1第4、5题。下节课内容:7.1.3三角形的稳定性
1、现有长度为2cm、3cm、4cm、5cm的木棒,从中任取三根,能组成三角形的个数为( )
A、1个 B、2个 C、3个 D、4个
2、如果一个三角形两边为2cm,7cm,且第三边为奇数,则第三边的长为 cm。
3、若等腰三角形的两边长为4,6,则等腰三角形周长为 。 C714或16请你任意作出一个△ABC,并回忆作出△ABC的高。 (2)三条高有什么特点?问题(1)什么是三角形的高。(从三角形的一个顶点向它的对边作垂线,顶点和垂足间的线段叫做三角形的高。)(三条高相交于一点)7.1.2三角形的高、中线与角平分线∟∟∟(3)你能用折纸的方法找出你准备好的三角形的三条高吗? (4)高的交点有何特别之处?(锐角三角形的高的交点在三角形内,直角三角形的高的交点是两直角边的交点,钝角三角形的高的交点在三角形外)请拿出你准备好的三角形纸片,在上面定义三个顶点分别为A、B、C,对折,使AC与AB所在直线重合,折痕与BC交于点D。请拿出你准备好的三角形纸片,在上面定义三个顶点分别为A、B、C,把B、C重合对折,折痕与BC交于点D。(演示)问题:(1)D点有什么特殊性?(2)连接线段AD,AD把△ABC分成的两个三角形的面积有何关系?(3)请归纳线段AD的特点。 (4)用语言描述中线定义。 (点D是线段AB的中点)(两个三角形的面积相等)(在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线)问题:(1)通过这个操作你认为AD有什么位置特点?(2)你能用尺规作出AD吗?(3)请给出三角形角平分线的定义。(把∠A分成两个相等的角)(三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。)演示(1)你认为一个三角形有几条高,几条中线,几条角平分线?并分别作出来。(3)你认为“三线”定义中,高与线段垂线、三角形角平分线与角的平分线、中线与线段中点有何异同?(2)通过本组作出的三线,请说明它们各自的共性。巩固新知:(都有三条)(都相交于一点)(三角形的高、角平分线、中线都是线段)练习:②AE是△ABC中线,那么BE= = BC。 ③如下图,在△ABC中∠BAC=60o,∠B=45o,AD是∠BAC的角平分线,求∠ADB的度数。∠CAD∠BACCE答案:∠ADB=1050解决问题㈠如右图,D、E分别为△ABC的边AC、BC的中点,下列说法正确吗?
(1)DE是△BDC的中线。
(2)BD是△ABC的中线。
(3)AD=CD,BE=EC。
总结归纳请同学们回忆一下本课主要内容,并谈谈你有什么收获? 三线高(线)中线角平分线都是由三角形的一个顶点到对边(或对边延长线)上的点连结的线段作业教科书75页习题7.1第4、5题。下节课内容:7.1.3三角形的稳定性
