江苏省淮安市涟水中学2013-2014学年高一下学期第二次模块检测数学试题
文档属性
| 名称 | 江苏省淮安市涟水中学2013-2014学年高一下学期第二次模块检测数学试题 | 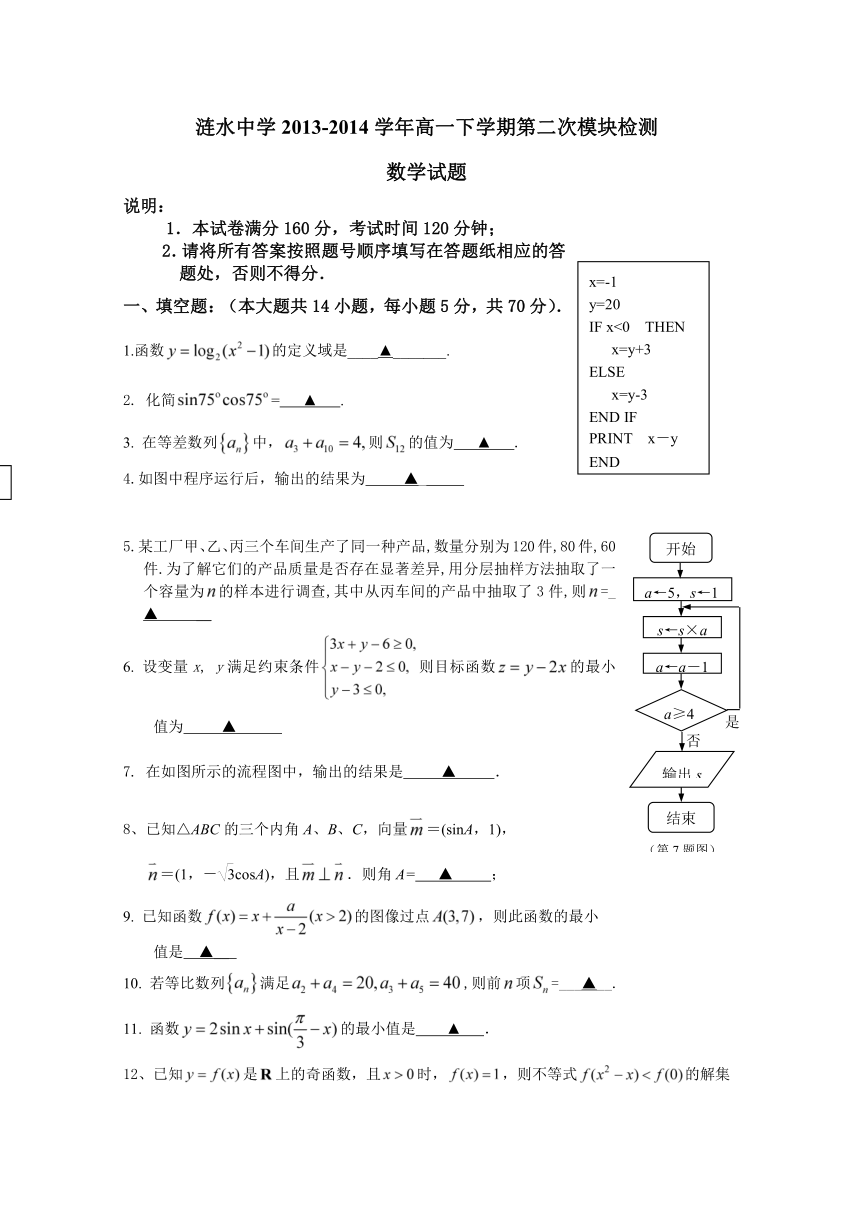 | |
| 格式 | zip | ||
| 文件大小 | 186.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-09 07:46:11 | ||
图片预览



文档简介
涟水中学2013-2014学年高一下学期第二次模块检测
数学试题
说明:
1.本试卷满分160分,考试时间120分钟;
2.请将所有答案按照题号顺序填写在答题纸相应的答题处,否则不得分.
一、填空题:(本大题共14小题,每小题5分,共70分).
1.函数的定义域是____▲_______.
2. 化简= ▲ .
3. 在等差数列中,则的值为 ▲ .
4.如图中程序运行后,输出的结果为 ▲_
5.某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为的样本进行调查,其中从丙车间的产品中抽取了3件,则=_ ▲ __
6. 设变量x, y满足约束条件则目标函数的最小值为 ▲
7. 在如图所示的流程图中,输出的结果是 ▲ .
8、已知△ABC的三个内角A、B、C,向量=(sinA,1),
=(1,-cosA),且.则角A= ▲ ;
9. 已知函数的图像过点,则此函数的最小
值是 ▲__
10. 若等比数列满足,则前项=___▲__.
11. 函数的最小值是 ▲ .
12、已知是上的奇函数,且时,,则不等式的解集为 ▲ .
13. 在中,分别是角的对边,且,则角的大小为 ▲
14.将正偶数排列如下表,其中第行第个数表示为,例如,若,
则 ▲ .
二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15、(本小题共14分)
在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,且 b2+c2=a2+bc.
(1)求∠A的大小;
(2)若a=,b+c=3,求面积.
16.(本题满分14分)
等差数列中,
(1)求的通项公式;
(2)设
17.(本题满分14分)
已知.
(1)求的值;
(2)求的值.
18. (本小题满分16分)
某厂家举行大型的促销活动,经测算某产品当促销费用为万元时,销售量万件满足(其中,). 现假定生产量与销售量相等,已知生产该产品万件还需投入成本万元(不含促销费用),产品的销售价格定为万元/万件.
⑴ 将该产品的利润万元表示为促销费用万元的函数;
⑵ 当促销费用投入多少万元时,厂家的利润最大.并求出最大利润。
19.(本小题满分16分)
已知向量,,,其中A、B、C分别是的三内角.
(1)求的值;
(2)求的最大值.
20.(本题满分16分)
已知数列的前项和(为正整数)。
(1) 令,求证:数列是等差数列,并求数列的通项公式;
(2) 令,,求使得成立的最小正整数,并证明你的结论.
2013-2014学年度高一年级第二学期阶段性测试
数学试题
15,解:(1)∵△ABC中,b2+c2=a2+bc
∴根据余弦定理,得cosA==………………4分
∵A∈(0,π),∴A=.………………………………7分
(2)由(1)得b2+c2﹣bc=a2=3
配方可得(b+c)2﹣3bc=3
∵b+c=3,∴32﹣3bc=3,可得bc=2……………………10分
…………………………14分
16.解:(1)设等差数列的公差为d,则
因为,所以.
解得,. ………………………………4分
所以的通项公式为. …………………………7分
(2), …………………………10分
所以. ……………………14分
17解:⑴由条件得; ………6分
⑵因为,所以, ………8分
因为,所以, ………9分
又,所以, ………10分
所以.……14分
19、解:(1)由
……………………………3分
∵,
……………………5分
化简得:……………………………………7分
即=4…………………………………………………………………………8分
(2)由(1)知:
∴…………………………………10分
…………………………………………………12分
因为故,所以,
当时的最小值是4.…………………………………………………14分
∴ …………………………………………………16分
20.解:(1)在中,令n=1,可得,即……………2分
当时,,
.……………2分
.
又数列是首项和公差均为1的等差数列. ……………5分
于是. ……………7分
(2)由(1)得,所以
……………9分
由①-②得
∴ ……………………………………………………………11分
∴ …………………………………13分
数学试题
说明:
1.本试卷满分160分,考试时间120分钟;
2.请将所有答案按照题号顺序填写在答题纸相应的答题处,否则不得分.
一、填空题:(本大题共14小题,每小题5分,共70分).
1.函数的定义域是____▲_______.
2. 化简= ▲ .
3. 在等差数列中,则的值为 ▲ .
4.如图中程序运行后,输出的结果为 ▲_
5.某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为的样本进行调查,其中从丙车间的产品中抽取了3件,则=_ ▲ __
6. 设变量x, y满足约束条件则目标函数的最小值为 ▲
7. 在如图所示的流程图中,输出的结果是 ▲ .
8、已知△ABC的三个内角A、B、C,向量=(sinA,1),
=(1,-cosA),且.则角A= ▲ ;
9. 已知函数的图像过点,则此函数的最小
值是 ▲__
10. 若等比数列满足,则前项=___▲__.
11. 函数的最小值是 ▲ .
12、已知是上的奇函数,且时,,则不等式的解集为 ▲ .
13. 在中,分别是角的对边,且,则角的大小为 ▲
14.将正偶数排列如下表,其中第行第个数表示为,例如,若,
则 ▲ .
二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15、(本小题共14分)
在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,且 b2+c2=a2+bc.
(1)求∠A的大小;
(2)若a=,b+c=3,求面积.
16.(本题满分14分)
等差数列中,
(1)求的通项公式;
(2)设
17.(本题满分14分)
已知.
(1)求的值;
(2)求的值.
18. (本小题满分16分)
某厂家举行大型的促销活动,经测算某产品当促销费用为万元时,销售量万件满足(其中,). 现假定生产量与销售量相等,已知生产该产品万件还需投入成本万元(不含促销费用),产品的销售价格定为万元/万件.
⑴ 将该产品的利润万元表示为促销费用万元的函数;
⑵ 当促销费用投入多少万元时,厂家的利润最大.并求出最大利润。
19.(本小题满分16分)
已知向量,,,其中A、B、C分别是的三内角.
(1)求的值;
(2)求的最大值.
20.(本题满分16分)
已知数列的前项和(为正整数)。
(1) 令,求证:数列是等差数列,并求数列的通项公式;
(2) 令,,求使得成立的最小正整数,并证明你的结论.
2013-2014学年度高一年级第二学期阶段性测试
数学试题
15,解:(1)∵△ABC中,b2+c2=a2+bc
∴根据余弦定理,得cosA==………………4分
∵A∈(0,π),∴A=.………………………………7分
(2)由(1)得b2+c2﹣bc=a2=3
配方可得(b+c)2﹣3bc=3
∵b+c=3,∴32﹣3bc=3,可得bc=2……………………10分
…………………………14分
16.解:(1)设等差数列的公差为d,则
因为,所以.
解得,. ………………………………4分
所以的通项公式为. …………………………7分
(2), …………………………10分
所以. ……………………14分
17解:⑴由条件得; ………6分
⑵因为,所以, ………8分
因为,所以, ………9分
又,所以, ………10分
所以.……14分
19、解:(1)由
……………………………3分
∵,
……………………5分
化简得:……………………………………7分
即=4…………………………………………………………………………8分
(2)由(1)知:
∴…………………………………10分
…………………………………………………12分
因为故,所以,
当时的最小值是4.…………………………………………………14分
∴ …………………………………………………16分
20.解:(1)在中,令n=1,可得,即……………2分
当时,,
.……………2分
.
又数列是首项和公差均为1的等差数列. ……………5分
于是. ……………7分
(2)由(1)得,所以
……………9分
由①-②得
∴ ……………………………………………………………11分
∴ …………………………………13分
同课章节目录
