江苏省淮安市涟水中学2014-2015学年高二上学期第一次模块检测数学试题
文档属性
| 名称 | 江苏省淮安市涟水中学2014-2015学年高二上学期第一次模块检测数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 161.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-08 22:54:32 | ||
图片预览


文档简介
涟水中学2014-2015学年高二上学期第一次模块检测
数学试题
考试时间120分钟,满分160分
一、填空题(14×5分=70分)
1.四面体共有_____条棱.
2.若直线平面,直线,则与的位置关系是_____________
3.过点且垂直于直线的直线方程为_______________
4.过点且平行于直线的直线方程为_______________
5.过点M(-2, a)和N(a,4)的直线的斜率为1,则实数a的值为____________
6.经过点且在y轴上截距为2的直线的方程为______________________
7.若三点共线 则的值为_________________
8.已知两个不同的平面和两条不重合的直线,有下列四个命题:
(1)若,则;(2)若,则;
(3)若,则;(4)若,则.
其中正确命题的个数为
9.设是两条不同的直线,是两个不同的平面,则下列四个命题中
(1)若,则;
(2)若,则;
(3)若,则;
(4)若,则.
其中所有真命题的序号是 .
10.已知直线与直线平行,则m=________
11.如图所示,已知一个多面体的平面展开图由一个边长为2的正方形和4个边长为2的正三角形组成,则该多面体的体积是________.
12.若曲线与直线()有两个公共点,则的取值范围是________
13. 直线的倾斜角的取值范围是_________________
14.设正三棱柱的所有顶点都在一个球面上,且该正三棱柱的底面边长为,侧棱长为2,则该球的表面积为________.
二、解答题:(第15、16、17、18题每题14分,第19题16分,第20题18分)
15.已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3),
(1)求AB边所在的直线方程;
(2)求AB边的高所在直线方程.
16.在直三棱柱中, , 为棱上任一点.
(1)求证:直线∥平面;
(2)求证:平面⊥平面.
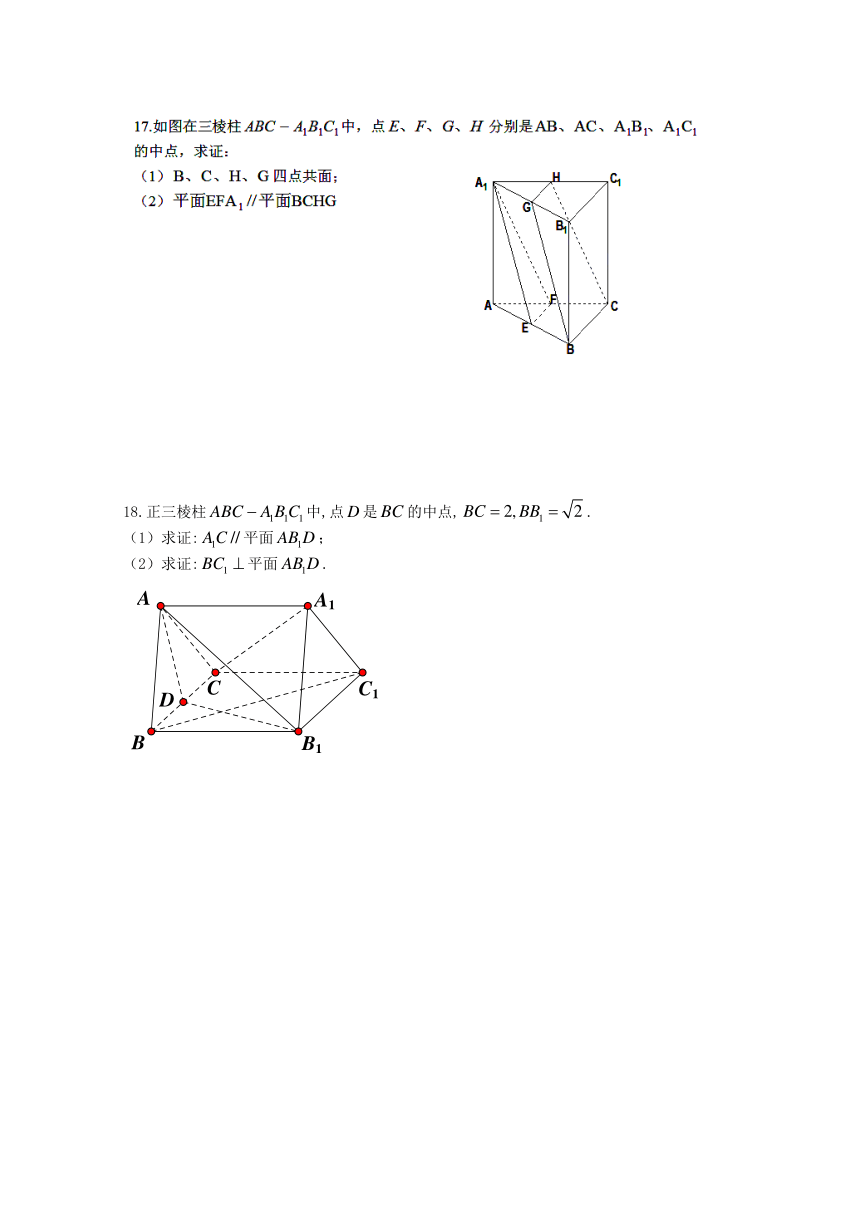
18.正三棱柱中,点是的中点,.
(1)求证:平面;
(2)求证:平面.
19.已知直线.
(1)证明直线过定点,并求出该定点的坐标;
(2)求直线与第二象限所围成三角形的面积的最小值,并求面积最小时直线的方程.
20.如图,等腰梯形ABEF中,AB//EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.
(1)求证:AF⊥平面CBF;
(2)在棱FC上是否存在点M,使得OM//平面DAF?
(3)求点A到平面BDF的距离.
命题、校对:陈开群,贾正兵 2014年9月
高二数学学分认定模块测试一参考答案
9.(1)(4)
10.-2
11.
12.a>2
13.
14.8π
15.(1)6x+y+1=0………………7分
(2)x-6y+14=0…………14分
16.(1)………………6分(漏线不在面内扣2分)
(2)………………8分(直接写扣2分,漏扣2分)
17.(1)…………6分(直接写GH//BC扣2分)
(2)…………8分(直接由线线平行证明面面平行扣4分,漏线线相交扣2分)
18.(1)连接
…………6分(漏线不在面内扣2分)
(2)设D为BC中点,∴AD⊥BC,
中,
………………13分
又
…………16分
19.(1)a(2x+y+1)+b(x+y-1)=0
得…………4分
∴直线恒过定点(-2,1)………………6分
(2)设直线的横截距纵截距分别为
∴直线的方程为…………8分
又∵…………12分
∴……14分
“=”号成立时,a=4,b=2,方程为x-2y+4=0…………16分
(3)…………16分(无证明过程扣3分)
达标分:
阳光班:130分
普通班:100分
数学试题
考试时间120分钟,满分160分
一、填空题(14×5分=70分)
1.四面体共有_____条棱.
2.若直线平面,直线,则与的位置关系是_____________
3.过点且垂直于直线的直线方程为_______________
4.过点且平行于直线的直线方程为_______________
5.过点M(-2, a)和N(a,4)的直线的斜率为1,则实数a的值为____________
6.经过点且在y轴上截距为2的直线的方程为______________________
7.若三点共线 则的值为_________________
8.已知两个不同的平面和两条不重合的直线,有下列四个命题:
(1)若,则;(2)若,则;
(3)若,则;(4)若,则.
其中正确命题的个数为
9.设是两条不同的直线,是两个不同的平面,则下列四个命题中
(1)若,则;
(2)若,则;
(3)若,则;
(4)若,则.
其中所有真命题的序号是 .
10.已知直线与直线平行,则m=________
11.如图所示,已知一个多面体的平面展开图由一个边长为2的正方形和4个边长为2的正三角形组成,则该多面体的体积是________.
12.若曲线与直线()有两个公共点,则的取值范围是________
13. 直线的倾斜角的取值范围是_________________
14.设正三棱柱的所有顶点都在一个球面上,且该正三棱柱的底面边长为,侧棱长为2,则该球的表面积为________.
二、解答题:(第15、16、17、18题每题14分,第19题16分,第20题18分)
15.已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3),
(1)求AB边所在的直线方程;
(2)求AB边的高所在直线方程.
16.在直三棱柱中, , 为棱上任一点.
(1)求证:直线∥平面;
(2)求证:平面⊥平面.
18.正三棱柱中,点是的中点,.
(1)求证:平面;
(2)求证:平面.
19.已知直线.
(1)证明直线过定点,并求出该定点的坐标;
(2)求直线与第二象限所围成三角形的面积的最小值,并求面积最小时直线的方程.
20.如图,等腰梯形ABEF中,AB//EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.
(1)求证:AF⊥平面CBF;
(2)在棱FC上是否存在点M,使得OM//平面DAF?
(3)求点A到平面BDF的距离.
命题、校对:陈开群,贾正兵 2014年9月
高二数学学分认定模块测试一参考答案
9.(1)(4)
10.-2
11.
12.a>2
13.
14.8π
15.(1)6x+y+1=0………………7分
(2)x-6y+14=0…………14分
16.(1)………………6分(漏线不在面内扣2分)
(2)………………8分(直接写扣2分,漏扣2分)
17.(1)…………6分(直接写GH//BC扣2分)
(2)…………8分(直接由线线平行证明面面平行扣4分,漏线线相交扣2分)
18.(1)连接
…………6分(漏线不在面内扣2分)
(2)设D为BC中点,∴AD⊥BC,
中,
………………13分
又
…………16分
19.(1)a(2x+y+1)+b(x+y-1)=0
得…………4分
∴直线恒过定点(-2,1)………………6分
(2)设直线的横截距纵截距分别为
∴直线的方程为…………8分
又∵…………12分
∴……14分
“=”号成立时,a=4,b=2,方程为x-2y+4=0…………16分
(3)…………16分(无证明过程扣3分)
达标分:
阳光班:130分
普通班:100分
同课章节目录
