1.1 空间向量及其运算——2023-2024学年高二数学人教A版(2019)选择性必修第一册课时分层练(含解析)
文档属性
| 名称 | 1.1 空间向量及其运算——2023-2024学年高二数学人教A版(2019)选择性必修第一册课时分层练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 399.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 08:03:26 | ||
图片预览



文档简介
1.1 空间向量及其运算
——2023-2024学年高二数学人教A版(2019)
选择性必修第一册课时分层练
【夯实基础】
知识点1 空间向量及其线性运算
1.空间中任意四个点,则( )
A. B. C. D.
2.已知空间向量a,b,且,,,则一定共线的三点是( )
A.A,B,D B.A,B,C C.B,C,D D.A,C,D
3.如图,在四面体OABC中,,,,点M在OA上,点N在BC上,且,,则( )
A. B.
C. D.
4.已知i,j,k是不共面向量,,,,若a,b,c三个向量共面,则实数等于___________.
知识点2 空间向量的数量积运算
5.如图,空间四边形的每条边和对角线长都等于1,点分别是的中点,则( )
A. B. C. D.
6.设为空间中的任意两个非零向量,有下列各式:
①;②;③;④.
其中正确的个数为( )
A.1 B.2 C.3 D.4
7.在正三棱柱中,若,则与所成角的大小为( ).
A. B. C. D.
8.已知空间向量a,b,c和实数,则下列说法正确的是( )
A.若,则或 B.若,则或
C.若,则或 D.若,则
【提升能力】
9.如图,在平行六面体中,与向量的模一定相等的向量有( )
A.0个 B.3个 C.7个 D.9个
10.已知A,B,C,D为空间中任意四个点,则等于( )
A. B. C. D.
11.已知四边形ABCD为矩形,平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积不一定为零的是( )
A.与 B.与 C.与 D.与
12.如图所示,在平行六面体中,,,,M是的中点,点N是上的点,且,用a,b,c表示向量的结果是( )
A. B. C. D.
13.(多选)对于空间一点O,下列命题中正确的是( ).
A.若,则P,A,B三点共线
B.若,则P是线段AB的中点
C.若,则P,A,B三点不共线
D.若,则B是线段AP的中点
14.(多选)已知长方体,则下列向量的数量积可以为0的是( )
A. B. C. D.
15.已知,,,,,,则__________.
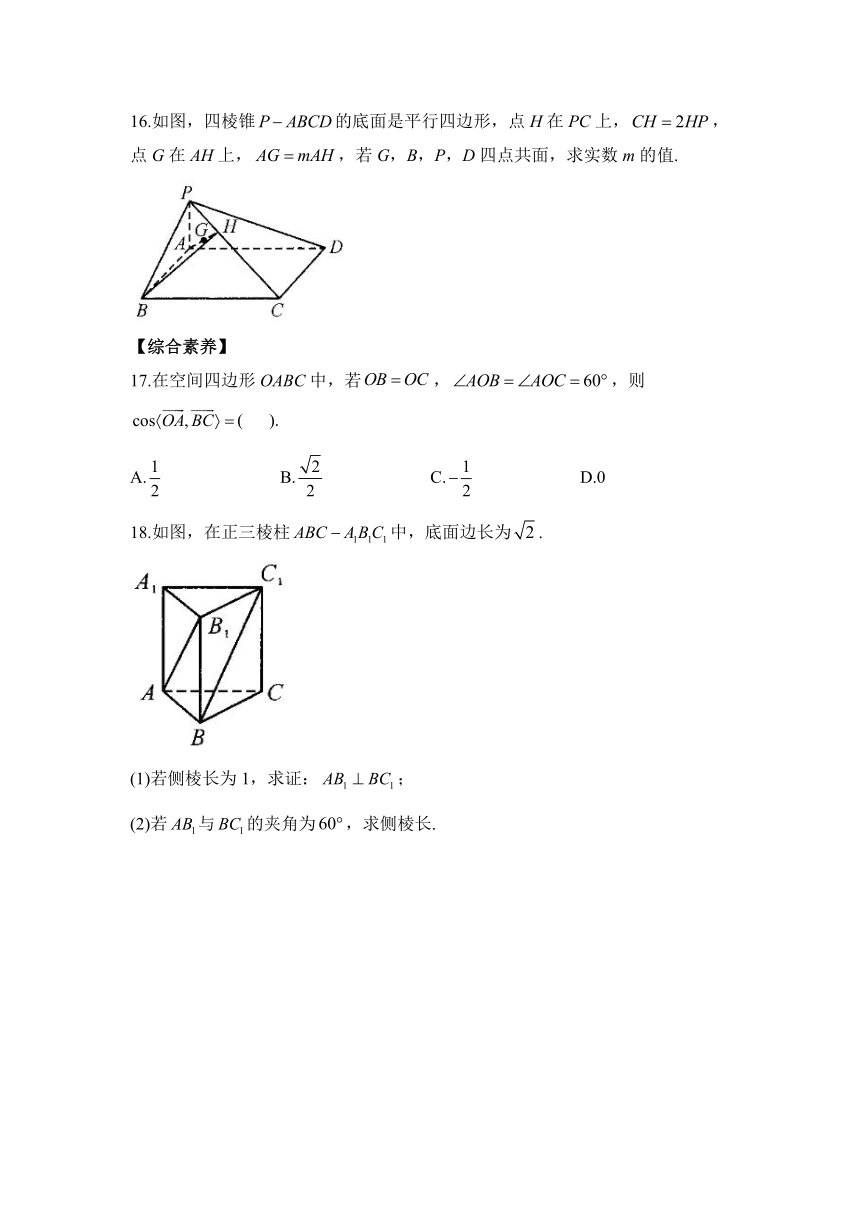
16.如图,四棱锥的底面是平行四边形,点H在PC上,,点G在AH上,,若G,B,P,D四点共面,求实数m的值.
【综合素养】
17.在空间四边形OABC中,若,,则( ).
A. B. C. D.0
18.如图,在正三棱柱中,底面边长为.
(1)若侧棱长为1,求证:;
(2)若与的夹角为,求侧棱长.
答案以及解析
1.答案:C
解析:利用空间向量运算法则即可得出.
2.答案:A
解析:,A,B,D三点共线,故选A.
3.答案:A
解析:如图,连接MB,则
.故选A.
4.答案:
解析:若向量a,b,c共面,则存在,使得,
,解得.
5.答案:B
解析:由题意得,所以.故选B.
6.答案:B
解析:由数量积的性质和运算律可知①④是正确的,故选B.
7.答案:B
解析:,,设,,则.
8.答案:B
解析:对于选项A,若,则或或,故A错误;
对于选项B,由,可得或,故B正确;
对于选项C,由,得,即向量, 的模相等,但方向不确定,故C错误;
对于选项D,由,得,则或或,故D错误.故选B.
9.答案:C
解析:向量的模相等即长度相等,根据平行六面体的性质可知,与向量的模一定相等的向量有,,,,,,,共7个.故选C.
10.答案:D
解析:.
11.答案:A
解析:由平面ABCD,及三垂线定理可知,,,故B,C,D选项中两向量的数量积为零,无法判断PC与BD是否存在垂直关系,故数量积不一定为零.
12.答案:D
解析:由题意可得,
.
,,
,故选D.
13.答案:ABD
解析:由得,知P,A,B三点共线,A正确;由得,知P是线段AB的中点,B正确;由得,知B是线段AP的中点,D正确.由得,知P,A,B三点共线,故C错误.
14.答案:ABC
解析:若,则,A正确;若,则,B正确;平面,,C正确;和BC分别为矩形的对角线和边,
两者不可能垂直,D错.故选ABC.
15.答案:
解析:,故.
16.答案:
解析:设,,,则,
,
.
因为G,B,P,D四点共面,所以向量,,共面,
于是,即,
所以,解得.
17.答案:D
解析:.
18.答案:(1)证明见解析
(2)侧棱长为2
解析:解:设,,,
则,,.
(1)由,得
,
所以,即.
(2)设,则,
,
又与的夹角为,
所以或,
所以,解得,即侧棱长为2.
——2023-2024学年高二数学人教A版(2019)
选择性必修第一册课时分层练
【夯实基础】
知识点1 空间向量及其线性运算
1.空间中任意四个点,则( )
A. B. C. D.
2.已知空间向量a,b,且,,,则一定共线的三点是( )
A.A,B,D B.A,B,C C.B,C,D D.A,C,D
3.如图,在四面体OABC中,,,,点M在OA上,点N在BC上,且,,则( )
A. B.
C. D.
4.已知i,j,k是不共面向量,,,,若a,b,c三个向量共面,则实数等于___________.
知识点2 空间向量的数量积运算
5.如图,空间四边形的每条边和对角线长都等于1,点分别是的中点,则( )
A. B. C. D.
6.设为空间中的任意两个非零向量,有下列各式:
①;②;③;④.
其中正确的个数为( )
A.1 B.2 C.3 D.4
7.在正三棱柱中,若,则与所成角的大小为( ).
A. B. C. D.
8.已知空间向量a,b,c和实数,则下列说法正确的是( )
A.若,则或 B.若,则或
C.若,则或 D.若,则
【提升能力】
9.如图,在平行六面体中,与向量的模一定相等的向量有( )
A.0个 B.3个 C.7个 D.9个
10.已知A,B,C,D为空间中任意四个点,则等于( )
A. B. C. D.
11.已知四边形ABCD为矩形,平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积不一定为零的是( )
A.与 B.与 C.与 D.与
12.如图所示,在平行六面体中,,,,M是的中点,点N是上的点,且,用a,b,c表示向量的结果是( )
A. B. C. D.
13.(多选)对于空间一点O,下列命题中正确的是( ).
A.若,则P,A,B三点共线
B.若,则P是线段AB的中点
C.若,则P,A,B三点不共线
D.若,则B是线段AP的中点
14.(多选)已知长方体,则下列向量的数量积可以为0的是( )
A. B. C. D.
15.已知,,,,,,则__________.
16.如图,四棱锥的底面是平行四边形,点H在PC上,,点G在AH上,,若G,B,P,D四点共面,求实数m的值.
【综合素养】
17.在空间四边形OABC中,若,,则( ).
A. B. C. D.0
18.如图,在正三棱柱中,底面边长为.
(1)若侧棱长为1,求证:;
(2)若与的夹角为,求侧棱长.
答案以及解析
1.答案:C
解析:利用空间向量运算法则即可得出.
2.答案:A
解析:,A,B,D三点共线,故选A.
3.答案:A
解析:如图,连接MB,则
.故选A.
4.答案:
解析:若向量a,b,c共面,则存在,使得,
,解得.
5.答案:B
解析:由题意得,所以.故选B.
6.答案:B
解析:由数量积的性质和运算律可知①④是正确的,故选B.
7.答案:B
解析:,,设,,则.
8.答案:B
解析:对于选项A,若,则或或,故A错误;
对于选项B,由,可得或,故B正确;
对于选项C,由,得,即向量, 的模相等,但方向不确定,故C错误;
对于选项D,由,得,则或或,故D错误.故选B.
9.答案:C
解析:向量的模相等即长度相等,根据平行六面体的性质可知,与向量的模一定相等的向量有,,,,,,,共7个.故选C.
10.答案:D
解析:.
11.答案:A
解析:由平面ABCD,及三垂线定理可知,,,故B,C,D选项中两向量的数量积为零,无法判断PC与BD是否存在垂直关系,故数量积不一定为零.
12.答案:D
解析:由题意可得,
.
,,
,故选D.
13.答案:ABD
解析:由得,知P,A,B三点共线,A正确;由得,知P是线段AB的中点,B正确;由得,知B是线段AP的中点,D正确.由得,知P,A,B三点共线,故C错误.
14.答案:ABC
解析:若,则,A正确;若,则,B正确;平面,,C正确;和BC分别为矩形的对角线和边,
两者不可能垂直,D错.故选ABC.
15.答案:
解析:,故.
16.答案:
解析:设,,,则,
,
.
因为G,B,P,D四点共面,所以向量,,共面,
于是,即,
所以,解得.
17.答案:D
解析:.
18.答案:(1)证明见解析
(2)侧棱长为2
解析:解:设,,,
则,,.
(1)由,得
,
所以,即.
(2)设,则,
,
又与的夹角为,
所以或,
所以,解得,即侧棱长为2.
