2023-2024学年人教版数学九年级上册第二十三章 旋转 单元检测卷 (无答案)
文档属性
| 名称 | 2023-2024学年人教版数学九年级上册第二十三章 旋转 单元检测卷 (无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 194.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 00:00:00 | ||
图片预览

文档简介
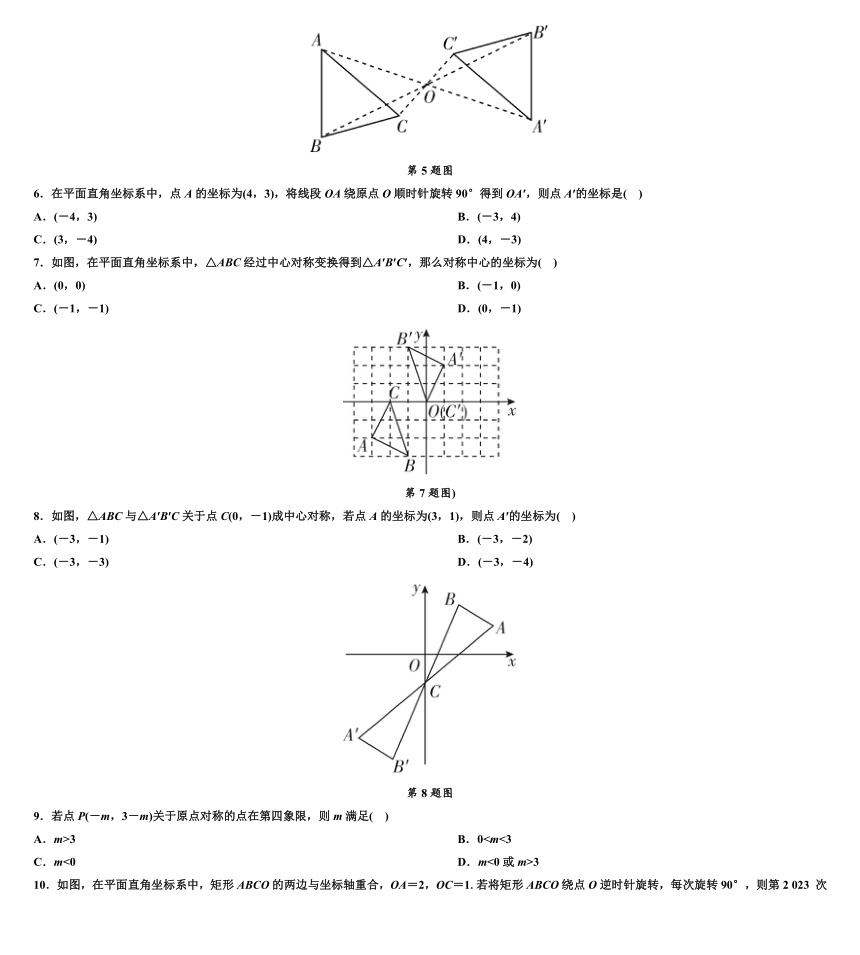
第二十三章检测卷
(满分:120分 时间:90分钟)
班级____________ 姓名____________ 学号____________
题 号 一 二 三 四 五 总 分
得 分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A B C D
2.下列物体的运动:①电梯上下迎送顾客;②风车的转动;③钟摆的摆动;④方向盘的转动.属于旋转的有( )
A.1种 B.2种
C.3种 D.4种
3.下列图形分别绕某个点旋转120°后不能与自身重合的是( )
A B C D
4.如图,将△AOB绕着点O顺时针旋转,得到△COD,若∠AOB=40°,∠BOC=30°,则旋转角度是( )
A.10° B.30°
C.40° D.70°
第4题图
5.如图,已知△ABC和△A′B′C′关于点O成中心对称,则下列结论错误的是( )
A.∠ABC=∠A′B′C′ B.∠AOB=∠A′OB′
C.AB=A′B′ D.OA=OB′
第5题图
6.在平面直角坐标系中,点A的坐标为(4,3),将线段OA绕原点O顺时针旋转90°得到OA′,则点A′的坐标是( )
A.(-4,3) B.(-3,4)
C.(3,-4) D.(4,-3)
7.如图,在平面直角坐标系中,△ABC经过中心对称变换得到△A′B′C′,那么对称中心的坐标为( )
A.(0,0) B.(-1,0)
C.(-1,-1) D.(0,-1)
第7题图)
8.如图,△ABC与△A′B′C关于点C(0,-1)成中心对称,若点A的坐标为(3,1),则点A′的坐标为( )
A.(-3,-1) B.(-3,-2)
C.(-3,-3) D.(-3,-4)
第8题图
9.若点P(-m,3-m)关于原点对称的点在第四象限,则m满足( )
A.m>3 B.0C.m<0 D.m<0或m>3
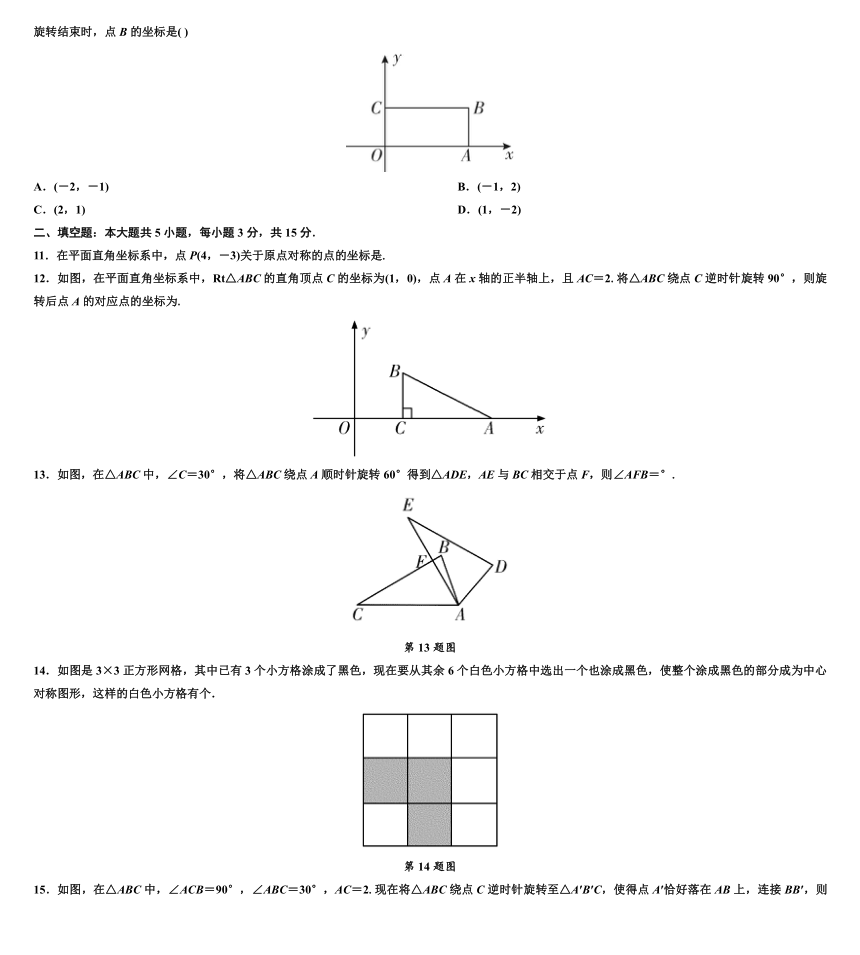
10.如图,在平面直角坐标系中,矩形ABCO的两边与坐标轴重合,OA=2,OC=1.若将矩形ABCO绕点O逆时针旋转,每次旋转90°,则第2 023 次旋转结束时,点B的坐标是( )
A.(-2,-1) B.(-1,2)
C.(2,1) D.(1,-2)
二、填空题:本大题共5小题,每小题3分,共15分.
11.在平面直角坐标系中,点P(4,-3)关于原点对称的点的坐标是.
12.如图,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴的正半轴上,且AC=2.将△ABC绕点C逆时针旋转90°,则旋转后点A的对应点的坐标为.
13.如图,在△ABC中,∠C=30°,将△ABC绕点A顺时针旋转60°得到△ADE,AE与BC相交于点F,则∠AFB=°.
第13题图
14.如图是3×3正方形网格,其中已有3个小方格涂成了黑色,现在要从其余6个白色小方格中选出一个也涂成黑色,使整个涂成黑色的部分成为中心对称图形,这样的白色小方格有个.
第14题图
15.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AC=2.现在将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,连接BB′,则BB′的长度为.
第15题图
三、解答题(一):本大题共3小题,每小题8分,共24分.
16.在平面直角坐标系中.
(1)画出△ABC关于原点对称的△A1B1C1;
(2)画出△ABC绕原点O顺时针旋转90°得到的△A2B2C2.
17.如图,把一个含有30°角的直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB延长线上的点E重合,其中点C的对应点为点D.
(1)三角尺旋转了度;
(2)△CBD是三角形;
(3)若BC=2,求△CBD的面积.
18.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′.
(1)若∠1=25°,则∠BAA′=°;
(2)若BC=1,AC=3,求△AA′B′的面积与周长.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图,正方形ABCD的对角线相交于点O,正方形A′B′C′O与正方形ABCD的边长相等,在正方形 A′B′C′O 绕点O旋转的过程中,两个正方形重叠部分的面积与正方形ABCD的面积有什么关系?请证明你的结论.
20.如图,点E是正方形ABCD内的一点,连接AE,BE,CE,将△ABE绕点B顺时针旋转90°到△CBF的位置,连接EF,若AE=1,BE=2.
(1)求EF的长;
(2)当CE=3时,求∠AEB的度数.
21.如图,在△ABC中,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BD,BE.
(1)判断△ABD的形状,并说明理由;
(2)求证:BE平分∠ABD.
五、解答题(三):本大题共2小题,每小题12分,共24分.
22.如图,在△ABC中,AB=AC,把△ABC绕A点顺时针旋转得到△ADE,连接BD,CE,交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
23.通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整.
原题:如图①,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连接EF,试猜想EF,BE,DF之间的数量关系.
(1)思路梳理
把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,由∠ADG=∠B=90°,得∠FDG=180°,即点F,D,G共线,易证△AFG≌,故EF,BE,DF之间的数量关系为.
(2)类比引申
如图②,点E,F分别在正方形ABCD的边CB,DC的延长线上,∠EAF=45°.连接EF,试猜想EF,BE,DF之间的数量关系,并证明.
(满分:120分 时间:90分钟)
班级____________ 姓名____________ 学号____________
题 号 一 二 三 四 五 总 分
得 分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A B C D
2.下列物体的运动:①电梯上下迎送顾客;②风车的转动;③钟摆的摆动;④方向盘的转动.属于旋转的有( )
A.1种 B.2种
C.3种 D.4种
3.下列图形分别绕某个点旋转120°后不能与自身重合的是( )
A B C D
4.如图,将△AOB绕着点O顺时针旋转,得到△COD,若∠AOB=40°,∠BOC=30°,则旋转角度是( )
A.10° B.30°
C.40° D.70°
第4题图
5.如图,已知△ABC和△A′B′C′关于点O成中心对称,则下列结论错误的是( )
A.∠ABC=∠A′B′C′ B.∠AOB=∠A′OB′
C.AB=A′B′ D.OA=OB′
第5题图
6.在平面直角坐标系中,点A的坐标为(4,3),将线段OA绕原点O顺时针旋转90°得到OA′,则点A′的坐标是( )
A.(-4,3) B.(-3,4)
C.(3,-4) D.(4,-3)
7.如图,在平面直角坐标系中,△ABC经过中心对称变换得到△A′B′C′,那么对称中心的坐标为( )
A.(0,0) B.(-1,0)
C.(-1,-1) D.(0,-1)
第7题图)
8.如图,△ABC与△A′B′C关于点C(0,-1)成中心对称,若点A的坐标为(3,1),则点A′的坐标为( )
A.(-3,-1) B.(-3,-2)
C.(-3,-3) D.(-3,-4)
第8题图
9.若点P(-m,3-m)关于原点对称的点在第四象限,则m满足( )
A.m>3 B.0
10.如图,在平面直角坐标系中,矩形ABCO的两边与坐标轴重合,OA=2,OC=1.若将矩形ABCO绕点O逆时针旋转,每次旋转90°,则第2 023 次旋转结束时,点B的坐标是( )
A.(-2,-1) B.(-1,2)
C.(2,1) D.(1,-2)
二、填空题:本大题共5小题,每小题3分,共15分.
11.在平面直角坐标系中,点P(4,-3)关于原点对称的点的坐标是.
12.如图,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴的正半轴上,且AC=2.将△ABC绕点C逆时针旋转90°,则旋转后点A的对应点的坐标为.
13.如图,在△ABC中,∠C=30°,将△ABC绕点A顺时针旋转60°得到△ADE,AE与BC相交于点F,则∠AFB=°.
第13题图
14.如图是3×3正方形网格,其中已有3个小方格涂成了黑色,现在要从其余6个白色小方格中选出一个也涂成黑色,使整个涂成黑色的部分成为中心对称图形,这样的白色小方格有个.
第14题图
15.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AC=2.现在将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,连接BB′,则BB′的长度为.
第15题图
三、解答题(一):本大题共3小题,每小题8分,共24分.
16.在平面直角坐标系中.
(1)画出△ABC关于原点对称的△A1B1C1;
(2)画出△ABC绕原点O顺时针旋转90°得到的△A2B2C2.
17.如图,把一个含有30°角的直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB延长线上的点E重合,其中点C的对应点为点D.
(1)三角尺旋转了度;
(2)△CBD是三角形;
(3)若BC=2,求△CBD的面积.
18.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′.
(1)若∠1=25°,则∠BAA′=°;
(2)若BC=1,AC=3,求△AA′B′的面积与周长.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图,正方形ABCD的对角线相交于点O,正方形A′B′C′O与正方形ABCD的边长相等,在正方形 A′B′C′O 绕点O旋转的过程中,两个正方形重叠部分的面积与正方形ABCD的面积有什么关系?请证明你的结论.
20.如图,点E是正方形ABCD内的一点,连接AE,BE,CE,将△ABE绕点B顺时针旋转90°到△CBF的位置,连接EF,若AE=1,BE=2.
(1)求EF的长;
(2)当CE=3时,求∠AEB的度数.
21.如图,在△ABC中,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BD,BE.
(1)判断△ABD的形状,并说明理由;
(2)求证:BE平分∠ABD.
五、解答题(三):本大题共2小题,每小题12分,共24分.
22.如图,在△ABC中,AB=AC,把△ABC绕A点顺时针旋转得到△ADE,连接BD,CE,交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
23.通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整.
原题:如图①,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连接EF,试猜想EF,BE,DF之间的数量关系.
(1)思路梳理
把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,由∠ADG=∠B=90°,得∠FDG=180°,即点F,D,G共线,易证△AFG≌,故EF,BE,DF之间的数量关系为.
(2)类比引申
如图②,点E,F分别在正方形ABCD的边CB,DC的延长线上,∠EAF=45°.连接EF,试猜想EF,BE,DF之间的数量关系,并证明.
同课章节目录
