7.3多边形内角和(06新人教版初一下)[下学期]
文档属性
| 名称 | 7.3多边形内角和(06新人教版初一下)[下学期] | 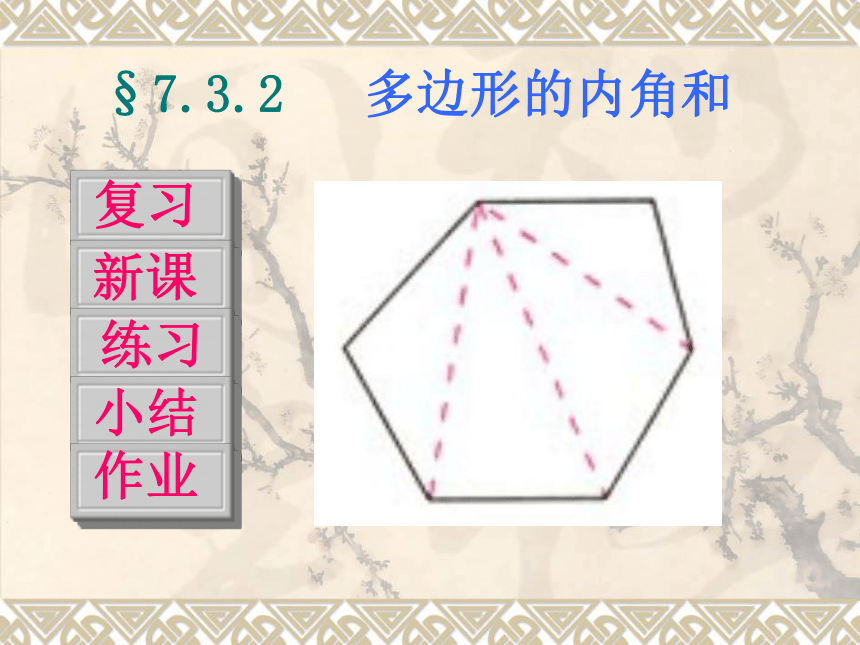 | |
| 格式 | rar | ||
| 文件大小 | 197.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-09 11:15:00 | ||
图片预览



文档简介
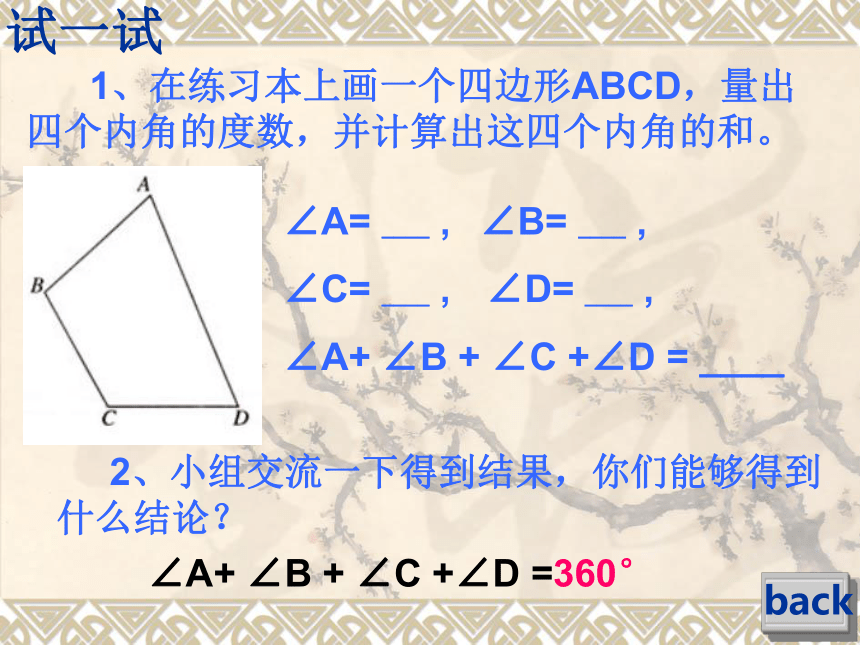
课件13张PPT。§7.3.2 多边形的内角和复习新课练习小结作业复习back3、什么叫做多边形的对角线?1、什么叫做多边形?2、什么叫做多边形的内角? 答:多边形相邻两边组成的角叫做多边形的内角。 答:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形。 答:连接多边形的不相邻的两个顶点的线段,叫做多边形的对角线。 back4、如下图,从五边形的一个顶点A出发,可以引什么条对角线?答:2条。
新课back 上节课我们学习了多边形,那么你知道哪些多边形的内角和呢? 答:三角形的内角和是180°;
特殊四边形(正方形、长方形等)的内角
和是360°。 那么其他四边形的内角和是多少?
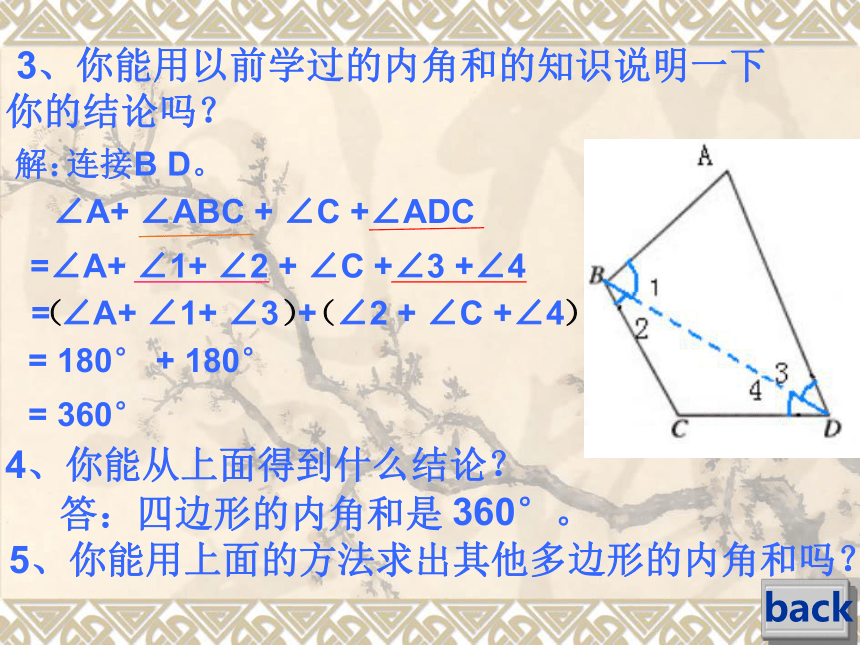
试一试back 1、在练习本上画一个四边形ABCD,量出四个内角的度数,并计算出这四个内角的和。∠A= ____ ,
∠B= ____ ,
∠C= ____ ,
∠D= ____ ,
∠A+ ∠B + ∠C +∠D = ____
2、小组交流一下得到结果,你们能够得到
什么结论?∠A+ ∠B + ∠C +∠D =360°
back 3、你能用以前学过的内角和的知识说明一下你的结论吗?∠A+ ∠ABC + ∠C +∠ADC
=∠A+ ∠1+ ∠2 + ∠C +∠3 +∠4
= ∠A+ ∠1+ ∠3 + ∠2 + ∠C +∠4
( )
( )
= 180° + 180°
= 360°
解:
4、你能从上面得到什么结论?
答:四边形的内角和是
360°。
5、你能用上面的方法求出其他多边形的内角和吗?
连接B D。
从五边形一个顶点出发可以引几条对角线? back5
6
2
3
3×180°=540 °
.
.
..
.
..
.
..
.
.3
4
4×180°=720°
(n-2)×180°
n
n-3
n-2
它们将五边形分成几个三角形?
那么这五边形的内角和为多少度 ?
六边形呢?
n 边形呢?
综上所述,设多边形的边数为n,则 n边形的内角和等于
(n一2)·180° 。
例1 back 如果一个四边形的一组对角互补,那么另一组对角有什么关系? 已知:四边形ABCD中∠A+∠C=180°.
求:∠B与∠D的关系.解:
如图,四边形ABCD中,
∠A+∠C=180°
∠A+∠B+∠C+∠D=(4-2) ×180 °= 360 °,
因为
∠B+∠D
= 360°-(∠A+∠C)
= 360 °-180°
=180°
所以
这就是说:如果四边形一组对角互补,那么另一组对角也互补.练习练习一练习二back (1)多边形的内角和随着边数的增加而____,
边数增加一条时,它的内角和增加____度.
(2)七边形的内角和等于____度.
(3)一个多边形的内角和等于720 °,那么
这个多边形是__边形.六
900
增加
180
(1)若12边形的每个内角都相等,那么它的 每个内角是多少度? 练习练习一练习二back (2)已知某个多边形的每个内角都是135°,
求这个多边形的边数。 解:
(2)设这个多边形的边数为n,
(1) 12边形的内角和为
(12-2) ×180°= 1800°
则它的每个内角为
1800°÷12= 150°
则根据题意及多边形内角和公式有:
180(n-2)=135n
n=8
解得
答:这个多边形的边数是8。
课堂小结
back本节课你学到了哪些知识?
(2)已知内角和如何求边数;
二、多边形的内角和公式的应用;一、多边形的内角和公式;
(1)已知边数如何求内角和;
多边形
内角和三角形
内角和转化n边形的内角和等于(n一2)·180° .作业
back课本P90 习题7.3 的2、9题 再见!谢谢大家,
欢迎提出宝贵意见!
新课back 上节课我们学习了多边形,那么你知道哪些多边形的内角和呢? 答:三角形的内角和是180°;
特殊四边形(正方形、长方形等)的内角
和是360°。 那么其他四边形的内角和是多少?
试一试back 1、在练习本上画一个四边形ABCD,量出四个内角的度数,并计算出这四个内角的和。∠A= ____ ,
∠B= ____ ,
∠C= ____ ,
∠D= ____ ,
∠A+ ∠B + ∠C +∠D = ____
2、小组交流一下得到结果,你们能够得到
什么结论?∠A+ ∠B + ∠C +∠D =360°
back 3、你能用以前学过的内角和的知识说明一下你的结论吗?∠A+ ∠ABC + ∠C +∠ADC
=∠A+ ∠1+ ∠2 + ∠C +∠3 +∠4
= ∠A+ ∠1+ ∠3 + ∠2 + ∠C +∠4
( )
( )
= 180° + 180°
= 360°
解:
4、你能从上面得到什么结论?
答:四边形的内角和是
360°。
5、你能用上面的方法求出其他多边形的内角和吗?
连接B D。
从五边形一个顶点出发可以引几条对角线? back5
6
2
3
3×180°=540 °
.
.
..
.
..
.
..
.
.3
4
4×180°=720°
(n-2)×180°
n
n-3
n-2
它们将五边形分成几个三角形?
那么这五边形的内角和为多少度 ?
六边形呢?
n 边形呢?
综上所述,设多边形的边数为n,则 n边形的内角和等于
(n一2)·180° 。
例1 back 如果一个四边形的一组对角互补,那么另一组对角有什么关系? 已知:四边形ABCD中∠A+∠C=180°.
求:∠B与∠D的关系.解:
如图,四边形ABCD中,
∠A+∠C=180°
∠A+∠B+∠C+∠D=(4-2) ×180 °= 360 °,
因为
∠B+∠D
= 360°-(∠A+∠C)
= 360 °-180°
=180°
所以
这就是说:如果四边形一组对角互补,那么另一组对角也互补.练习练习一练习二back (1)多边形的内角和随着边数的增加而____,
边数增加一条时,它的内角和增加____度.
(2)七边形的内角和等于____度.
(3)一个多边形的内角和等于720 °,那么
这个多边形是__边形.六
900
增加
180
(1)若12边形的每个内角都相等,那么它的 每个内角是多少度? 练习练习一练习二back (2)已知某个多边形的每个内角都是135°,
求这个多边形的边数。 解:
(2)设这个多边形的边数为n,
(1) 12边形的内角和为
(12-2) ×180°= 1800°
则它的每个内角为
1800°÷12= 150°
则根据题意及多边形内角和公式有:
180(n-2)=135n
n=8
解得
答:这个多边形的边数是8。
课堂小结
back本节课你学到了哪些知识?
(2)已知内角和如何求边数;
二、多边形的内角和公式的应用;一、多边形的内角和公式;
(1)已知边数如何求内角和;
多边形
内角和三角形
内角和转化n边形的内角和等于(n一2)·180° .作业
back课本P90 习题7.3 的2、9题 再见!谢谢大家,
欢迎提出宝贵意见!
