2023浙教版科学八年级上册暑假“胜人一筹”专题训练(五):浮力的计算【含解析】
文档属性
| 名称 | 2023浙教版科学八年级上册暑假“胜人一筹”专题训练(五):浮力的计算【含解析】 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2023-07-27 00:00:00 | ||
图片预览



文档简介
浮力的计算
1.如图所示是一种木质圆柱形“菱桶”,是江南地区采菱时的载人工具。已知菱桶的底面积为2米2,高约25厘米,质量为20千克,请通过计算回答问题:
(1)一只空“菱桶”放入水中静止时受到的浮力是多少?
(2)若图中采菱人的重量为600牛,为了保证安全,“菱桶”露出水面高度不能低于5厘米,则“菱桶”内最多可放多少千克的菱角?
2.如图是小宝研究弹簧测力计的示数F与物体A下表面离水面的距离h的关系实验装置,其中A是底面积为25cm2的实心均匀圆柱形物体,用弹簧测力计提着物体A,使其缓慢浸入水中(水未溢出),得到F与h的关系图像如图中实线所示。(g=10N/kg)
(1)物体A重为3N,将它放在水平桌面上时对桌面的压强为多少帕?
(2)完全浸没时,A受到水的浮力及密度为多少?
(3)小宝换用另一种未知液体重复上述实验并绘制出如图中虚线所示图像,则该液体密度为多大?
3. 2021年7月,河南省郑州市连遭暴雨袭击引发全民关注,造成了重大的人员伤亡和经济损失。救援队通常利用冲锋舟转移民众至安全地区,如图所示。已知某一型号冲锋舟的质量为300千克,最大排水体积为1.2米3。试回答以下问题:(河水的密度为1.0×103千克/米3)
(1)洪水是我国危害最大的自然灾害之一,以下关于洪水的说法错误的是_____
A.持续性暴雨和台风是引发洪水的主要自然因素
B.破坏植被会使洪水的危害性增大
C.人类活动不会对洪水造成影响
(2)一艘上述型号的空冲锋舟漂浮在水上时受到的浮力多大?
(3)假设一个成年人的质量为60千克,为了保证安全,该冲锋舟最多能载多少个成年人?
4.小杭同学有一张总体积为0.3平方米的质量分布均匀的长方体塑料泡沫床垫,将其放入水中时,床垫有1/5体积浸没在水中,求:
(1)此时床垫受到的浮力多大?
(2)床垫的密度是多少?
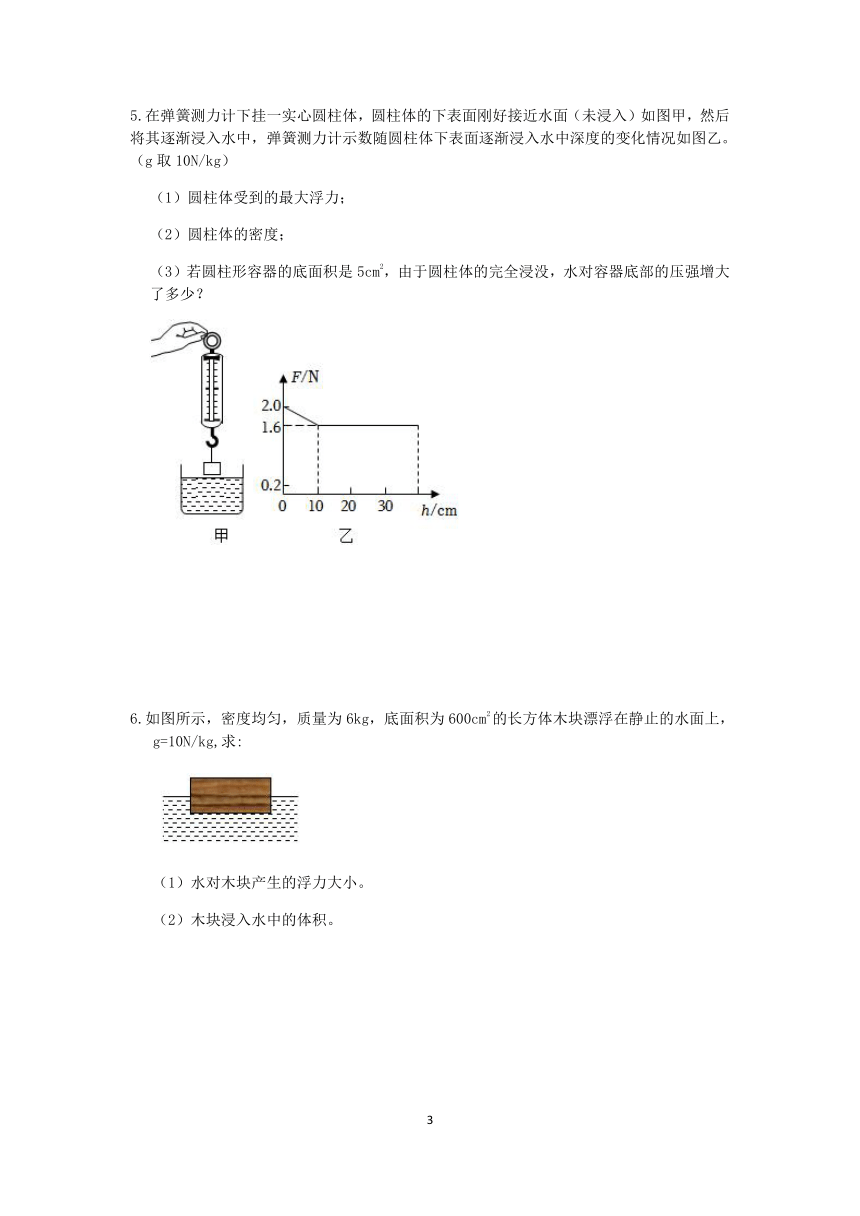
5.在弹簧测力计下挂一实心圆柱体,圆柱体的下表面刚好接近水面(未浸入)如图甲,然后将其逐渐浸入水中,弹簧测力计示数随圆柱体下表面逐渐浸入水中深度的变化情况如图乙。(g取10N/kg)
(1)圆柱体受到的最大浮力;
(2)圆柱体的密度;
(3)若圆柱形容器的底面积是5cm2,由于圆柱体的完全浸没,水对容器底部的压强增大了多少?
6.如图所示,密度均匀,质量为6kg,底面积为600cm2的长方体木块漂浮在静止的水面上,g=10N/kg,求:
(1)水对木块产生的浮力大小。
(2)木块浸入水中的体积。
7.如图所示,圆柱形容器底面积是200cm2,里面装有水,水深为0.5m,水中有一个不吸水的实心塑料块被细线系着,塑料块的体积为5×10﹣3m3,塑料块的密度为0.6×103kg/m3,g=10N/kg,试求:
(1)此时塑料块受到的浮力是多大?
(2)此时绳子的拉力。
(3)绳子剪断前后水对容器底的压强变化了多少?
8.水平桌面上放置一底面积为100cm2,重为6N的柱形容器,容器内装有20cm深的某液体,将一体积为400cm3的物体A悬挂在弹簧测力计上,弹簧测力计示数为10N,让物体从液面上方逐渐浸入直到浸没在液体中(如图),弹簧测力计示数变为5.2N。(柱形容器的厚度忽略不计,容器内液体没有溢出,物体未接触器底)求:
(1)物体浸没在液体中时受到的浮力;
(2)容器内液体的密度;
(3)物体浸没时容器对桌面的压强。
9.重为8N的物体挂在弹簧测力计下面,浸没在如图所示圆柱形容器的水中,此时弹簧测力计的示数为6N,求:
(1)物体受到的浮力;
(2)物体的密度
10.弹簧测力计能测力大小,也能“测”物质密度。如图,用细线系住金属块挂在弹簧测力计上,先后在空气中、浸没在水和盐水中测量,读数分别为F1=2.7N、F2=1.7N,F3=1.5N。请求出:
(1)金属块在水中受到的浮力;
(2)金属块的密度;
(3)盐水的密度。
11.某同学学习了浮力的有关知识后,制作了一台,浮力秤”,可方便地称量物体的质量,其构造如图所示。已知小筒底面积为0.01平方米,小筒的高度是0.2米,小筒和秤盘总重为 6N。
(1)秤盘上不放物体,此时浮力秤浸入的深度是多少?(即零刻度线所在位置)
(2)该浮力秤最多能称量多少质量的物体?(即量程)
12.如图所示,有个足够大的水池,在其水平池底以不同的方式放置一个木块,木块规格为1米×1米×2米,密度为0.6×103千克/米3。
(1)木块的重力是多少牛?
(2)未注水时,甲中木块对水平池底的压强为多少帕?
(3)甲、乙两种放置方式,往水池内加水,木块漂浮时,木块排开水的体积甲 = 乙(选填“<”、“=”、“>”)。
(4)当乙水池内注水深度达到0.8米时,求乙中木块所受的浮力。
13.如图是小勇研究弹簧测力计的示数F与物体A下表面离水面的距离h的关系实验装置。其中A是底面积为50cm2的实心均匀圆柱形物体。用弹簧测力计提着物体A,使其缓慢浸入水中(水未溢出),得到F与h的关系图像如图中实线所示。求:
(1)完全浸没时,物体A受到水的浮力。
(2)物体A的高。
(3)物体A的密度。
(4)小勇换用另一种未知液体重复上述实验并绘制出图中虚线所示图像,求该液体密度。
14.如图所示,用细绳将一物体系在装有水的薄壁柱形容器底部,浸没。物体所受浮力为10N,容器底面积50cm2,若不计绳重:
(1)求物体的体积;
(2)若细绳对物体的拉力为4N,求物体的密度;
(3)若剪断细绳,容器液面高度如何改变?请简要说明。
15.如图甲所示,用弹簧秤悬挂一物体,保持静止,当物体浸没在水中静止时弹簧测力计的示数如图乙所示,(ρ水=1×103kg/m3)g=10N/kg)
求:
(1)物体浸没在水中受到的浮力F浮;
(2)物体的密度ρ。
(3)若用细线悬挂一个体积不变的木球(ρ木=0.5×103kg/m3)使二者悬浮,如图丙所示,则木球的体积至少多大?
16.如图一体积为V的冰块漂浮在水面上,已知ρ冰=0.9×103kg/m3,不考虑水的蒸发,当冰块完全熔化后:
(1)液面将 (选填“上升”、“下降”、“不变”);
(2)运用有关知识证明你的观点。
17.体积V=0.2×10-3m3的物块A竖直挂在弹簧测力计下,在空气中静止时弹簧测力计的示数F1=2.6N,将物块A浸没在水中,静止时弹簧测力计的示数为F2,如图所示。求:
(1)物块A浸没在水中受到的浮力F浮;
(2)弹簧测力计的示数为F2;
(3)求物块A的密度。
18.将一挂在弹簧测力计下的形状不规则的石块分别浸没在水和盐水中,弹簧测力计的示数如图所示。g取10N/kg. 求:
(1)石块在水中所受到的浮力。
(2)石块的体积;
(3)石块的密度;
(4)盐水的密度;
19.如图甲所示,一弹簧测力计下悬挂底面积为40cm2的圆柱体,水平桌面上放置底面积为100cm2,质量为500g的圆筒,筒内装有30cm深的某液体。现将圆柱体从圆筒上方离液面某一高度处缓缓下降,然后将其逐渐浸入液体中,弹簧测力计的示数F与圆柱体下降高度h变化关系图像如图乙所示(圆筒的厚度忽略不计,圆柱体下降过程中没有液体从筒中溢出,g取10N/kg)。求:
(1)圆柱体完全浸没时受到液体的浮力;
(2)筒内液体密度;
(3)当圆柱体完全浸没时,圆筒对桌面的压强。
20.如图甲所示,长方体金属块在细绳竖直向上拉力作用下从水中开始一直竖直向上做匀速直线运动,上升到离水面一定的高度处。如图乙是绳子拉力F随时间t变化的图像。根据图像信息,求:(g取10N/kg)
(1)金属块的质量。
(2)金属块在水中受到的最大浮力。
(3)金属块的密度。
21. 2021年4月23日,长征18号核潜艇在海南某军港交付海军服役,这是我国现役最先进的战略核潜艇,标志着我国海军的作战实力又上升了一个新台阶。据报道,该核潜艇潜在水下时最大排水量为12000吨,漂浮时最大排水量为9000吨,下潜深度大于300米。(ρ海水取1.0×103kg/m3)
(1)核潜艇在水中是通过 来实现上浮和下沉的。
(2)以水上最大排水量漂浮在海水中时,核潜艇受到的浮力大小是多少
(3)核潜艇悬停在海水中时,若其内部储水舱排出3000吨海水后逐渐上浮,最终漂浮在海面上,则核潜艇漂浮时露出海面的体积是多少?
22.在科技节小发明活动中,小科制作了如图甲所示的液体密度计。往内筒中加入深为10cm的待测液体,当内筒稳定时,便可通过外筒壁上的刻度读出该待测液体的密度。己知内筒的质量为0.2kg,横截面积为20cm2。
(1)不加液体时,通过计算求出该小筒所受的浮力。
(2)向内筒中加入10cm深的某液体,稳定后发现外筒中的水面与内筒的18cm刻度线相平,如图乙所示。通过计算,求出此时与水面相平的外筒上标记的密度值。
(3)如果要增大该装置的测量范围,你的建议是
答案及解析
1.(1)解:空“菱桶”静止时漂浮在水上
F浮=G桶=mg=20kg×10N/kg=20N
(2)解:“菱桶”刚好露出水面5厘米时,浸在水中的深度为25cm-5cm=20厘米=0.2m
V排=2m2×0.2m=0.4m3
G总=F浮=ρ水gV排=1×103kg/m3×10N/Kg×0.4m3=4000N
G菱=4000N-600N-200N=3200N
m菱=G菱÷g=3200N÷10N/kg=320千克
【解析】【分析】(1)当物体漂浮在水面上时,它受到的浮力等于重力,即F浮=G;
(2)根据h浸入=h-h露计算出“菱桶”浸入水里的深度,再根据 V排= Sh浸计算出“菱桶”排开水的体积,接下来根据 G总=F浮=ρ水gV排 计算出 “菱桶”、人和菱角的总重力,根据G菱=G总-G桶-G人计算出菱角的重力,最后根据计算出菱角的质量。
2.解:
(1)由图乙可知,当h=0时,弹簧测力计的示数为3N,即物体A的重力G=3N,
物体A放在水平桌面上时,对桌面的压力:F=G=3N,
它对桌面的压强:p1200Pa;
(2)由图乙可知,物体完全浸没时弹簧测力计的示数F′=1N,
则物体A受到水的浮力:F浮=G﹣F′=3N﹣1N=2N;
根据阿基米德原理可知A的体积V=V排2×10﹣4m3;
A的质量m0.3kg,
A的密度ρ1.5×103kg/m3;
(3)由图乙可知,物体完全浸没在未知液体中时弹簧测力计的示数F″=1.4N,
物体A受到未知液体的浮力:F浮′=G﹣F″=3N﹣1.4N=1.6N,
物体浸没在未知液体中时其排开液体的体积V排′=V=2×10﹣4m3,
根据阿基米德原理可知该液体的密度:
ρ液0.8×103kg/m3。
答:(1)将它放在水平桌面上时对桌面的压强为1200Pa;
(2)完全浸没时,A受到水的浮力及密度分别为2N、1.5×103kg/m3;
(3)该液体密度为0.8×103kg/m3。
3.(1)C
(2)F浮=G=mg=300kg×10N/kg=3000N
(3)F浮最大=ρ液gV排=1.0×103kg/m3×10N/kg×1.2m3=12000N
G人总=12000N-3000N=9000N
G人=mg=60kg×10N/kg=600N
n=9000N/600N=15(人)
【解析】【分析】(1)根据对洪水的成因和治理等知识分析判断。
(2)当物体漂浮在液面上时,它受到的浮力等于重力,即F浮=G;
(3)当冲锋舟完全浸没在水中时,它排开水的体积等于自身体积,首先根据阿基米德原理 F浮最大=ρ液gV排 计算出它能够受到的最大浮力,再根据G总=F浮-G舟计算出所能承载的最大重力,最后根据计算出最多能载的人数。
【解答】(1)A.持续性暴雨和台风是引发洪水的主要自然因素,故A正确不合题意;
B.破坏植被会使洪水的危害性增大,故B正确不合题意;
C.人类活动大量的砍伐树木,破坏植被,会造成洪水和泥石流,故C错误符合题意。
故选C。
4.解:(1)床垫排开水的体积:V排V0.3m3=0.06m3,
床垫受到的浮力:F浮=ρ水gV排=1000kg/m3×10N/kg×0.06m3=600N;
(2)床垫漂浮时受到的浮力等于自身的重力,则床垫重力G=F浮=600N,
床垫的质量:m60kg,
床垫的密度:ρ0.2×103kg/m3;
答:(1)此时床垫受到的浮力600N;
(2)床垫的密度是0.2×103kg/m3。
5.解:(1)当h=0(圆柱体没有浸入水),弹簧测力计的示数等于圆柱体重,
由F﹣h图象可知,圆柱体重G=F1=2.0N,
当圆柱体全浸入时,弹簧测力计的示数F2=1.6N,
圆柱体受到的最大浮力(全浸入时):
F浮=G﹣F2=2N﹣1.6N=0.4N;
(2)由G=mg可得,圆柱体的质量:
m0.2kg,
由F浮=ρ水gV排得圆柱体浸没时排开水的体积:
V排4×10﹣5m3,
因为圆柱体浸没在水中,
所以圆柱体的体积V=V排=4×10﹣5m3,
圆柱体的密度:
ρ物5×103kg/m3;
(3)由于圆柱体的完全浸没,排开水的体积V排=4×10﹣5m3,
则水面上升的高度:
Δh0.08m,
水对容器底部的压强增大值:
Δp=ρgΔh=1×103kg/m3×10N/kg×0.08m=800Pa。
答:(1)圆柱体受到的最大浮力为0.4N;
(2)圆柱体的密度为5×103kg/m3;
(3)由于圆柱体的完全浸没,水对容器底部的压强增大了800Pa。
6.(1)由于物体是漂浮在水面上,因此F浮=G浮,G=mg=6kg×10N/kg=60N。
(2)根据阿基米德原理,,因此木块浸入水的体积是6×10-3m3。
【解析】【分析】(1)当木块漂浮在水面上时,F浮=G浮。
(2)根据阿基米德原理解答。
7.解:(1)浸没在水中的塑料块受到的浮力为:
F浮=G排=ρ水gV排=ρ水gV=1.0×103kg/m3×10N/kg×5×10﹣3m3=50N;
(2)塑料块所受重力为:
G=mg=ρ塑料Vg=0.6×103kg/m3×5×10﹣3m3×10N/kg=30N;
静止在水中的木块受到三个力(重力G、拉力F、浮力F浮)的作用,且满足受力平衡;即G+F=F浮;
故此时绳子的拉力为:
F=F浮﹣G=50N﹣30N=20N;
(3)绳子剪断之后,由于塑料块的密度小于水的密度,所以塑料块漂浮,塑料块受到的浮力等于塑料块的重力,所以F浮′=30N;
此时塑料块排开水的体积为:
V排′3×10﹣3m3,
此时塑料块排开水的体积比完全浸没在水中少排开水的体积为:
ΔV=V排﹣V排′=5×10﹣3m3﹣3×10﹣3m3=2×10﹣3m3,
此时容器水面降低的深度为:
h0.1m,
所以剪断绳子后,水对容器底减小的压强为:
Δp=ρgh=1.0×103kg/m3×10N/kg×0.1m=1000Pa。
答:(1)此时塑料块受到的浮力是50N;
(2)此时绳子的拉力为20N;
(3)绳子剪断前后水对容器底的压强变化了1000Pa。
8.(1)10N-5.2N=4.8N,因此物体浸没在液体中时受到的浮力为4.8N。
(2) 0.48kg÷0.0004m3=1.2×103kg/m3
因此容器内液体的密度为1.2×103kg/m3
(3)液体的体积V液=100cm2×20cm=2000cm3=2×10-3m3,
液体的重力G液=m液g=ρ液V液g=1.2×103kg/ m3×2×10-3m3×10N/kg=24N,
容器对桌面的压力F=(G液+G容器+G物)-F拉=(24N+6N+10N)-5.2N=34.8 N,
受力面积:S=100 cm2=10-2m2,
p==3480Pa。
【解析】【分析】(1)物体所受浮力使弹簧测力计示数减小。
(2)根据阿基米德原理物体所受浮力是排出液体所受重力,求出液体质量,根据密度公式求出液体密度。
(3)先求出物体和容器对桌面的压力,根据公式p=,求出物体浸没时容器对桌面的压强。
9.(1)解: 物体受到的浮力:F浮=G-F拉=8N-6N=2N;
(2)解:
该物体的体积:;
该物体的密度:。
【解析】【分析】(1)根据F浮=G-F拉计算物体受到的浮力;
(2)首先根据计算出物体的体积,再根据计算物体的密度。
10.(1)解:
(2)解:
(3)解:
【解析】【分析】(1)根据F浮=G-F拉计算金属块在水中受到的浮力;
(2)当金属块完全浸没在水中时,它排开水的体积等于自身体积,即 ,据此计算出金属块的体积,再根据 计算出金属块的质量,最后根据 计算出金属块的密度。
(3)首先根据F浮=G-F拉计算出金属块在盐水中受到的浮力,再根据阿基米德原理的变形式 计算出盐水的密度。
11.(1)秤盘上不放物体,始终在水面漂浮,即浮力等于重力,
即F浮力=G=ρ液gV排;
6N=103kg/m3×10N/kg×(0.01m2×h浸);
解得:h浸=0.06m;
(2)当浮力秤上物体的质量最大时,此时小筒和秤盘的总重和物体的重力之和等于此时受到的浮力,
即F浮力'=G总+G;
ρ液gV排'=G总+G;
103kg/m3×10N/kg×(0.01m2×0.2)=6N+m×10N/kg;
解得:m=1.4kg。
【解析】【分析】(1)浮力秤始终在水面漂浮,即浮力等于重力,将阿基米德原理F浮=ρ液gV排代入计算即可;
(2)当浮力秤上物体的质量最大时,小筒浸入的深度为0.2m,此时小筒和秤盘的总重和物体的重力之和等于此时受到的浮力,根据二力平衡的知识计算即可。
12.解:(1)由ρ可知,木块的质量为:
m=ρV=0.6×103kg/m3×1m×1m×2m=1200kg,
木块的重力为:
G=mg=1200kg×10N/kg=1.2×104N;
(2)未注水时,甲中木块对水平池底的压力为:
F=G=1.2×104N,
此时甲中木块对水平池底的压强为:
p6000Pa;
(3)物体漂浮时,浮力等于重力,因此两种放置方式木块受到的浮力相等,由F浮=ρ水gV排可知,木块排开水的体积相等;
(3)木块漂浮时,由F浮=G可得ρ水gV排=ρ木gV,
即V排V1m×1m×2m=1.2m3,
当水池内注水深度达到0.8米时,以乙方式放置,淹没的体积为V排乙=1m×1m×0.8m=0.8m3,
淹没的体积小于木块漂浮的体积,所以乙中木块沉底,乙中木块的浮力为:
F乙=ρ水gV乙=1.0×103kg/m3×10N/kg×0.8m3=8×103N。
答:(1)木块的重力为1.2×104N;
(2)未注水时,甲中木块对水平池底的压强为6000Pa;
(3)=;
(4)当乙水池内注水深度达到0.8米时,乙中木块所受的浮力为8×103N。
13.(1)当h=0时,弹簧测力计的示数为6N,即物体A的重力G=6N,完全浸没在水中:F浮=G-F=6N-2N=4N
(2)完全浸没在水中:
F浮=液gV排
V=V排=
液=1.0103kg/m3
V排===410-4m3=400cm3
V排=sh
物体A的高 h=
(3)根据公式
得m=
因为V=410-4m3
所以== 1.5×103kg/m3
(4)当h=0时,弹簧测力计的示数为6N,即物体A的重力G=6N,完全浸没在水中:F浮=G-F=6N-2.8N=3.2N,
V排=410-4m3
14.解:(1)物体浸没在水中时物体的体积:
V=V排1×10﹣3m3;
(2)物体受到重力、拉力和浮力,物体的重力:G=F浮﹣F=10N﹣4N=6N,
物体的质量:m0.6kg,
物体的密度:ρ0.6×103kg/m3;
(3)物体的密度小于水的密度,将细线剪断后,静止时,漂浮,此时物体受到的浮力:F浮=G=6N,
漂浮时排开水的体积:
V排′6×10﹣4m3,
液面下降的深度为:
Δh0.08m。
答:(1)物体的体积是1×10﹣3m3;
(2)若细绳对物体的拉力为4N,求物体的密度是0.6×103kg/m3;
(3)若剪断细绳,容器液面高度降低了0.08m。
15.(1)解:F浮=G﹣F′=6N﹣4N=2N
(2)解:因物体浸没时排开液体的体积和自身的体积相等,所以,由F浮=ρ水gV排可得,
物体的体积:V=V排= = =2×10﹣4m3,
由G=mg可得,物体的质量:m= = =0.6kg,
物体的密度:ρ= = =3×103kg/m3
(3)解:把木球和物体看做一个整体,受到竖直向上的总浮力和竖直向下的总重力,
因二者悬浮,所以,由力的平衡条件可得:F浮+F浮′=G+G木﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
设木球体积为V,把F浮′=ρ水gV排′和G木=m木g=ρ木Vg代入①式可得:
F浮+ρ水gV=G+ρ木Vg﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②
则木球的体积:V= = =8×10﹣4m3
【解析】【分析】(1)浸没在水中的物体受到竖直向上的浮力和拉力,竖直向下的重力,根据F浮=G-F计算物体受到的浮力;
(2)首先根据 计算出物体的体积,再根据计算出物体的质量,最后根据计算出物体的密度;
(3)将木球和物体看作一个整体,它们在水中悬浮,则它们受到的总浮力等于总重力,据此列出关系式,然后用阿基米德原理 F浮=ρ水gV排 和密度公式将其拆开,代入数据计算出木球的体积。
16.解:
由于冰块漂浮,F浮=G冰,由阿基米原理:F浮=G排;又因为冰熔化前后重力不变,
G冰=G冰化水即有:G排=G冰化水,
因为:F浮=G排=ρ水V排g,G冰=G冰化水=ρ水V冰化水g,
所以:ρ水V排g=ρ水V冰化水g,
故V排=V冰化水
所以冰熔化前后水面不升也不降。
故答案为:(1)不变;(2)见解答部分。
17.(1)物块A浸没在水中受到的浮力F浮=ρ液gV排=103kg/m3×10N/kg×0.2×10-3m3=2N;
(2)弹簧测力计的示数:F2=F拉=G-F浮=2.6N-2N=0.6N;
(3)物块A的密度:。
【解析】【分析】(1)根据阿基米德原理F浮=ρ液gV排计算出物体浸没时受到的浮力;
(2)根据F拉=G-F浮计算出浸没时弹簧测力计的示数F2;
(3)根据公式计算出物体的密度。
18.(1)根据甲乙两图可知,石块在水中受到的浮力:F浮力=G-F拉=4N-3N=1N;
(2)石块的体积;
(3)石块的密度;
(4)根据甲丙两图可知,石块在盐水中受到的浮力:F浮力'=G-F拉'=4N-2.9N=1.1N;
则盐水的密度为:。
【解析】【分析】(1)根据甲乙两图,利用公式F浮力=G-F拉计算出石块在水中受到的浮力;
(2)根据计算石块的体积;
(3)根据公式计算出石块的密度;
(4)根据甲丙两图,利用公式F浮力'=G-F拉'计算出石块在盐水中受到的浮力,再根据计算盐水的密度。
19.(1)由图象知,当h=0时,此时弹簧测力计的示数为18N,圆柱体的重力等于弹簧测力计的示数,则G=18N;
当h≥17cm时,弹簧测力计的示数不变,说明此时浮力不变,圆柱体完全浸没,此时圆柱体受到的拉力F拉=12N;
圆柱体浸没液体时受到的浮力:F浮=G-F拉=18N-12N=6N;
(2)由图知从7cm时弹簧测力计的示数逐渐减小,到17cm弹簧测力计的示数不变,
所以圆柱体额高度为:17cm-7cm=10cm,
圆柱体浸没在液体中,排开液体的体积:V排=V=Sh=40cm2×10cm=400cm3=4×10-4m3,
液体的密度:;
(3)液体的体积:V液=S′h液=100cm2×30cm=3000cm3=3×10-3m3,
液体的质量:m液=ρ液V液=1.5×103kg/m3×3×10-3m3=4.5kg,
将圆柱体、圆筒、液体看做一个整体,
圆筒对地面的压力:F=(m液+m筒)g+G-F拉=(4.5kg+0.5kg)×10N/kg+18N-12N=56N,
受力面积S=100cm2=0.01m2,
圆筒对地面的压强:。
【解析】【分析】(1)根据图象分析出物体的重力、完全浸没时受到的拉力,利用称重法测浮力F浮=G-F拉求圆柱体浸没液体时受到的浮力;
(2)求出了圆柱体浸没液体时受到的浮力,求出圆柱体的体积(浸没时排开液体的体积),利用F浮=ρ液gV排求液体的密度;
(3)此时圆筒对桌面的压力等于圆筒、圆柱体、液体的总重减去圆柱体受到的拉力,知道受力面积大小,利用 求圆筒对桌面的压强。
20.(1)解:∵对图乙中CD段物体受力分析可知:F=G=54N
∴m= = =5.4kg
(2)解:∵对图乙中AB段物体受力分析可知:F浮+F=G
∴F浮=G-F=54N-34N=20N
(3)解:V=V排= = =2×10-3m3
ρ= =2.7×103kg/m3
【解析】【分析】当物体完全浸没水中时,它排开水的体积不变,则它受到的浮力不变,根据F拉=G-F浮可知,此时绳子的拉力不变。当物体开始露出水面时,它排开水的体积变小,则它受到的浮力变小,因此绳子的拉力变大。当物体完全露出水面后,它不再受到浮力,此时绳子的拉力等于重力。
(1)根据图乙确定该物体的重力,然后根据 计算出它的质量。
(2)根据图乙确定该物体完全浸没时绳子的拉力,再根据 F浮=G-F 计算出它受到的最大浮力。
(3)当物体完全浸没时,它排开水的体积等于自身体积,即 ,然后根据 计算出金属块的密度。
21. (1)改变自身重力
(2)解:漂浮时,F浮= G排= m排g=9ⅹ106kgⅹ10N/kg=9×107N
答:核潜艇以水上最大排水量漂浮在海水中时受到的浮力为9×107牛。
(3)解:核潜艇以水下最大排水量悬停在海水中时,F悬浮=G排下=G
排出3000t海水后,核潜艇漂浮在海面上时,F漂浮=G排=G’
则核潜艇前后浮力的减少量为:△F浮=F悬浮-F漂浮=G-G’=△G= Dmg=3ⅹ106kgⅹ10N/kg=3×107N
V露=ΔV排= =3×103m3
【解析】【分析】(1)核潜艇在水中浸没时排开水的体积不变,即它受到的浮力不变,要改变浮沉状态,就只能改变自身重力,即通过调节水仓中海水的重力实现浮沉变化。
(2)根据阿基米德原理F浮=G排=m排g计算出漂浮时受到的浮力;
(3)核潜艇漂浮与悬浮时排开液体的体积不同则所受浮力不同,根据核潜艇悬浮与漂浮时的浮力差,利用阿基米德原理F浮=ρ液gV排计算悬浮与漂浮时排开液体体积的差值,即核潜艇漂浮时露出海面的体积。
22.(1)解:不加液体时,内筒处于漂浮状态,受到的浮力F浮=G桶=m桶g=0.2kg×10N/kg=2N
(2)解:当内筒的18cm刻度与水面相平时,内筒受到的浮力F浮=ρ水gV排=ρ水gSh浸=1.0×103kg/m3×10N/kg×20×10-4m2×0.18m=3.6N
小桶的重力G桶=m桶g=0.2kg×10N/kg=2N
根据漂浮条件可得,小筒内液体的重力G液=F浮-G桶=3.6N-2N=1.6N
小桶内液体的质量m液= = =0.16N
小桶内液体的体积为 V液=Sh液=20×10-4m2×0.1m=2×10-4m3
小桶内液体的密度 ρ= = =0.8×103kg/m3
(2)如果要增大该装置的测量范围,需要让内筒在没有放入液体前浸入水中的体积减小,根据F浮=ρ液gV排知要想使排开液体的体积减小,需要增大外筒中液体的密度;或减小内筒的重力使内筒受到的浮力减小,或减小每次倒入液体的深度使内筒的总重力减小,从而减小浮力。
【解析】【分析】(1)小筒始终在液面漂浮,根据漂浮条件计算出不加液体时小筒受到的浮力;
(2)当内筒的18cm刻度与水面相平时,首先根据阿基米德原理 F浮=ρ水gV排=ρ水gSh浸 计算出此时内筒受到的浮力,然后根据 G桶=m桶g 计算出小桶的重力,接下来根据 G液=F浮-G桶 计算出小桶内液体的重力,利用 计算出液体的质量,最后根据 计算出液体的密度。
(3)根据阿基米德原理F浮=ρ液gV排分析增大测量范围的方法。
1.如图所示是一种木质圆柱形“菱桶”,是江南地区采菱时的载人工具。已知菱桶的底面积为2米2,高约25厘米,质量为20千克,请通过计算回答问题:
(1)一只空“菱桶”放入水中静止时受到的浮力是多少?
(2)若图中采菱人的重量为600牛,为了保证安全,“菱桶”露出水面高度不能低于5厘米,则“菱桶”内最多可放多少千克的菱角?
2.如图是小宝研究弹簧测力计的示数F与物体A下表面离水面的距离h的关系实验装置,其中A是底面积为25cm2的实心均匀圆柱形物体,用弹簧测力计提着物体A,使其缓慢浸入水中(水未溢出),得到F与h的关系图像如图中实线所示。(g=10N/kg)
(1)物体A重为3N,将它放在水平桌面上时对桌面的压强为多少帕?
(2)完全浸没时,A受到水的浮力及密度为多少?
(3)小宝换用另一种未知液体重复上述实验并绘制出如图中虚线所示图像,则该液体密度为多大?
3. 2021年7月,河南省郑州市连遭暴雨袭击引发全民关注,造成了重大的人员伤亡和经济损失。救援队通常利用冲锋舟转移民众至安全地区,如图所示。已知某一型号冲锋舟的质量为300千克,最大排水体积为1.2米3。试回答以下问题:(河水的密度为1.0×103千克/米3)
(1)洪水是我国危害最大的自然灾害之一,以下关于洪水的说法错误的是_____
A.持续性暴雨和台风是引发洪水的主要自然因素
B.破坏植被会使洪水的危害性增大
C.人类活动不会对洪水造成影响
(2)一艘上述型号的空冲锋舟漂浮在水上时受到的浮力多大?
(3)假设一个成年人的质量为60千克,为了保证安全,该冲锋舟最多能载多少个成年人?
4.小杭同学有一张总体积为0.3平方米的质量分布均匀的长方体塑料泡沫床垫,将其放入水中时,床垫有1/5体积浸没在水中,求:
(1)此时床垫受到的浮力多大?
(2)床垫的密度是多少?
5.在弹簧测力计下挂一实心圆柱体,圆柱体的下表面刚好接近水面(未浸入)如图甲,然后将其逐渐浸入水中,弹簧测力计示数随圆柱体下表面逐渐浸入水中深度的变化情况如图乙。(g取10N/kg)
(1)圆柱体受到的最大浮力;
(2)圆柱体的密度;
(3)若圆柱形容器的底面积是5cm2,由于圆柱体的完全浸没,水对容器底部的压强增大了多少?
6.如图所示,密度均匀,质量为6kg,底面积为600cm2的长方体木块漂浮在静止的水面上,g=10N/kg,求:
(1)水对木块产生的浮力大小。
(2)木块浸入水中的体积。
7.如图所示,圆柱形容器底面积是200cm2,里面装有水,水深为0.5m,水中有一个不吸水的实心塑料块被细线系着,塑料块的体积为5×10﹣3m3,塑料块的密度为0.6×103kg/m3,g=10N/kg,试求:
(1)此时塑料块受到的浮力是多大?
(2)此时绳子的拉力。
(3)绳子剪断前后水对容器底的压强变化了多少?
8.水平桌面上放置一底面积为100cm2,重为6N的柱形容器,容器内装有20cm深的某液体,将一体积为400cm3的物体A悬挂在弹簧测力计上,弹簧测力计示数为10N,让物体从液面上方逐渐浸入直到浸没在液体中(如图),弹簧测力计示数变为5.2N。(柱形容器的厚度忽略不计,容器内液体没有溢出,物体未接触器底)求:
(1)物体浸没在液体中时受到的浮力;
(2)容器内液体的密度;
(3)物体浸没时容器对桌面的压强。
9.重为8N的物体挂在弹簧测力计下面,浸没在如图所示圆柱形容器的水中,此时弹簧测力计的示数为6N,求:
(1)物体受到的浮力;
(2)物体的密度
10.弹簧测力计能测力大小,也能“测”物质密度。如图,用细线系住金属块挂在弹簧测力计上,先后在空气中、浸没在水和盐水中测量,读数分别为F1=2.7N、F2=1.7N,F3=1.5N。请求出:
(1)金属块在水中受到的浮力;
(2)金属块的密度;
(3)盐水的密度。
11.某同学学习了浮力的有关知识后,制作了一台,浮力秤”,可方便地称量物体的质量,其构造如图所示。已知小筒底面积为0.01平方米,小筒的高度是0.2米,小筒和秤盘总重为 6N。
(1)秤盘上不放物体,此时浮力秤浸入的深度是多少?(即零刻度线所在位置)
(2)该浮力秤最多能称量多少质量的物体?(即量程)
12.如图所示,有个足够大的水池,在其水平池底以不同的方式放置一个木块,木块规格为1米×1米×2米,密度为0.6×103千克/米3。
(1)木块的重力是多少牛?
(2)未注水时,甲中木块对水平池底的压强为多少帕?
(3)甲、乙两种放置方式,往水池内加水,木块漂浮时,木块排开水的体积甲 = 乙(选填“<”、“=”、“>”)。
(4)当乙水池内注水深度达到0.8米时,求乙中木块所受的浮力。
13.如图是小勇研究弹簧测力计的示数F与物体A下表面离水面的距离h的关系实验装置。其中A是底面积为50cm2的实心均匀圆柱形物体。用弹簧测力计提着物体A,使其缓慢浸入水中(水未溢出),得到F与h的关系图像如图中实线所示。求:
(1)完全浸没时,物体A受到水的浮力。
(2)物体A的高。
(3)物体A的密度。
(4)小勇换用另一种未知液体重复上述实验并绘制出图中虚线所示图像,求该液体密度。
14.如图所示,用细绳将一物体系在装有水的薄壁柱形容器底部,浸没。物体所受浮力为10N,容器底面积50cm2,若不计绳重:
(1)求物体的体积;
(2)若细绳对物体的拉力为4N,求物体的密度;
(3)若剪断细绳,容器液面高度如何改变?请简要说明。
15.如图甲所示,用弹簧秤悬挂一物体,保持静止,当物体浸没在水中静止时弹簧测力计的示数如图乙所示,(ρ水=1×103kg/m3)g=10N/kg)
求:
(1)物体浸没在水中受到的浮力F浮;
(2)物体的密度ρ。
(3)若用细线悬挂一个体积不变的木球(ρ木=0.5×103kg/m3)使二者悬浮,如图丙所示,则木球的体积至少多大?
16.如图一体积为V的冰块漂浮在水面上,已知ρ冰=0.9×103kg/m3,不考虑水的蒸发,当冰块完全熔化后:
(1)液面将 (选填“上升”、“下降”、“不变”);
(2)运用有关知识证明你的观点。
17.体积V=0.2×10-3m3的物块A竖直挂在弹簧测力计下,在空气中静止时弹簧测力计的示数F1=2.6N,将物块A浸没在水中,静止时弹簧测力计的示数为F2,如图所示。求:
(1)物块A浸没在水中受到的浮力F浮;
(2)弹簧测力计的示数为F2;
(3)求物块A的密度。
18.将一挂在弹簧测力计下的形状不规则的石块分别浸没在水和盐水中,弹簧测力计的示数如图所示。g取10N/kg. 求:
(1)石块在水中所受到的浮力。
(2)石块的体积;
(3)石块的密度;
(4)盐水的密度;
19.如图甲所示,一弹簧测力计下悬挂底面积为40cm2的圆柱体,水平桌面上放置底面积为100cm2,质量为500g的圆筒,筒内装有30cm深的某液体。现将圆柱体从圆筒上方离液面某一高度处缓缓下降,然后将其逐渐浸入液体中,弹簧测力计的示数F与圆柱体下降高度h变化关系图像如图乙所示(圆筒的厚度忽略不计,圆柱体下降过程中没有液体从筒中溢出,g取10N/kg)。求:
(1)圆柱体完全浸没时受到液体的浮力;
(2)筒内液体密度;
(3)当圆柱体完全浸没时,圆筒对桌面的压强。
20.如图甲所示,长方体金属块在细绳竖直向上拉力作用下从水中开始一直竖直向上做匀速直线运动,上升到离水面一定的高度处。如图乙是绳子拉力F随时间t变化的图像。根据图像信息,求:(g取10N/kg)
(1)金属块的质量。
(2)金属块在水中受到的最大浮力。
(3)金属块的密度。
21. 2021年4月23日,长征18号核潜艇在海南某军港交付海军服役,这是我国现役最先进的战略核潜艇,标志着我国海军的作战实力又上升了一个新台阶。据报道,该核潜艇潜在水下时最大排水量为12000吨,漂浮时最大排水量为9000吨,下潜深度大于300米。(ρ海水取1.0×103kg/m3)
(1)核潜艇在水中是通过 来实现上浮和下沉的。
(2)以水上最大排水量漂浮在海水中时,核潜艇受到的浮力大小是多少
(3)核潜艇悬停在海水中时,若其内部储水舱排出3000吨海水后逐渐上浮,最终漂浮在海面上,则核潜艇漂浮时露出海面的体积是多少?
22.在科技节小发明活动中,小科制作了如图甲所示的液体密度计。往内筒中加入深为10cm的待测液体,当内筒稳定时,便可通过外筒壁上的刻度读出该待测液体的密度。己知内筒的质量为0.2kg,横截面积为20cm2。
(1)不加液体时,通过计算求出该小筒所受的浮力。
(2)向内筒中加入10cm深的某液体,稳定后发现外筒中的水面与内筒的18cm刻度线相平,如图乙所示。通过计算,求出此时与水面相平的外筒上标记的密度值。
(3)如果要增大该装置的测量范围,你的建议是
答案及解析
1.(1)解:空“菱桶”静止时漂浮在水上
F浮=G桶=mg=20kg×10N/kg=20N
(2)解:“菱桶”刚好露出水面5厘米时,浸在水中的深度为25cm-5cm=20厘米=0.2m
V排=2m2×0.2m=0.4m3
G总=F浮=ρ水gV排=1×103kg/m3×10N/Kg×0.4m3=4000N
G菱=4000N-600N-200N=3200N
m菱=G菱÷g=3200N÷10N/kg=320千克
【解析】【分析】(1)当物体漂浮在水面上时,它受到的浮力等于重力,即F浮=G;
(2)根据h浸入=h-h露计算出“菱桶”浸入水里的深度,再根据 V排= Sh浸计算出“菱桶”排开水的体积,接下来根据 G总=F浮=ρ水gV排 计算出 “菱桶”、人和菱角的总重力,根据G菱=G总-G桶-G人计算出菱角的重力,最后根据计算出菱角的质量。
2.解:
(1)由图乙可知,当h=0时,弹簧测力计的示数为3N,即物体A的重力G=3N,
物体A放在水平桌面上时,对桌面的压力:F=G=3N,
它对桌面的压强:p1200Pa;
(2)由图乙可知,物体完全浸没时弹簧测力计的示数F′=1N,
则物体A受到水的浮力:F浮=G﹣F′=3N﹣1N=2N;
根据阿基米德原理可知A的体积V=V排2×10﹣4m3;
A的质量m0.3kg,
A的密度ρ1.5×103kg/m3;
(3)由图乙可知,物体完全浸没在未知液体中时弹簧测力计的示数F″=1.4N,
物体A受到未知液体的浮力:F浮′=G﹣F″=3N﹣1.4N=1.6N,
物体浸没在未知液体中时其排开液体的体积V排′=V=2×10﹣4m3,
根据阿基米德原理可知该液体的密度:
ρ液0.8×103kg/m3。
答:(1)将它放在水平桌面上时对桌面的压强为1200Pa;
(2)完全浸没时,A受到水的浮力及密度分别为2N、1.5×103kg/m3;
(3)该液体密度为0.8×103kg/m3。
3.(1)C
(2)F浮=G=mg=300kg×10N/kg=3000N
(3)F浮最大=ρ液gV排=1.0×103kg/m3×10N/kg×1.2m3=12000N
G人总=12000N-3000N=9000N
G人=mg=60kg×10N/kg=600N
n=9000N/600N=15(人)
【解析】【分析】(1)根据对洪水的成因和治理等知识分析判断。
(2)当物体漂浮在液面上时,它受到的浮力等于重力,即F浮=G;
(3)当冲锋舟完全浸没在水中时,它排开水的体积等于自身体积,首先根据阿基米德原理 F浮最大=ρ液gV排 计算出它能够受到的最大浮力,再根据G总=F浮-G舟计算出所能承载的最大重力,最后根据计算出最多能载的人数。
【解答】(1)A.持续性暴雨和台风是引发洪水的主要自然因素,故A正确不合题意;
B.破坏植被会使洪水的危害性增大,故B正确不合题意;
C.人类活动大量的砍伐树木,破坏植被,会造成洪水和泥石流,故C错误符合题意。
故选C。
4.解:(1)床垫排开水的体积:V排V0.3m3=0.06m3,
床垫受到的浮力:F浮=ρ水gV排=1000kg/m3×10N/kg×0.06m3=600N;
(2)床垫漂浮时受到的浮力等于自身的重力,则床垫重力G=F浮=600N,
床垫的质量:m60kg,
床垫的密度:ρ0.2×103kg/m3;
答:(1)此时床垫受到的浮力600N;
(2)床垫的密度是0.2×103kg/m3。
5.解:(1)当h=0(圆柱体没有浸入水),弹簧测力计的示数等于圆柱体重,
由F﹣h图象可知,圆柱体重G=F1=2.0N,
当圆柱体全浸入时,弹簧测力计的示数F2=1.6N,
圆柱体受到的最大浮力(全浸入时):
F浮=G﹣F2=2N﹣1.6N=0.4N;
(2)由G=mg可得,圆柱体的质量:
m0.2kg,
由F浮=ρ水gV排得圆柱体浸没时排开水的体积:
V排4×10﹣5m3,
因为圆柱体浸没在水中,
所以圆柱体的体积V=V排=4×10﹣5m3,
圆柱体的密度:
ρ物5×103kg/m3;
(3)由于圆柱体的完全浸没,排开水的体积V排=4×10﹣5m3,
则水面上升的高度:
Δh0.08m,
水对容器底部的压强增大值:
Δp=ρgΔh=1×103kg/m3×10N/kg×0.08m=800Pa。
答:(1)圆柱体受到的最大浮力为0.4N;
(2)圆柱体的密度为5×103kg/m3;
(3)由于圆柱体的完全浸没,水对容器底部的压强增大了800Pa。
6.(1)由于物体是漂浮在水面上,因此F浮=G浮,G=mg=6kg×10N/kg=60N。
(2)根据阿基米德原理,,因此木块浸入水的体积是6×10-3m3。
【解析】【分析】(1)当木块漂浮在水面上时,F浮=G浮。
(2)根据阿基米德原理解答。
7.解:(1)浸没在水中的塑料块受到的浮力为:
F浮=G排=ρ水gV排=ρ水gV=1.0×103kg/m3×10N/kg×5×10﹣3m3=50N;
(2)塑料块所受重力为:
G=mg=ρ塑料Vg=0.6×103kg/m3×5×10﹣3m3×10N/kg=30N;
静止在水中的木块受到三个力(重力G、拉力F、浮力F浮)的作用,且满足受力平衡;即G+F=F浮;
故此时绳子的拉力为:
F=F浮﹣G=50N﹣30N=20N;
(3)绳子剪断之后,由于塑料块的密度小于水的密度,所以塑料块漂浮,塑料块受到的浮力等于塑料块的重力,所以F浮′=30N;
此时塑料块排开水的体积为:
V排′3×10﹣3m3,
此时塑料块排开水的体积比完全浸没在水中少排开水的体积为:
ΔV=V排﹣V排′=5×10﹣3m3﹣3×10﹣3m3=2×10﹣3m3,
此时容器水面降低的深度为:
h0.1m,
所以剪断绳子后,水对容器底减小的压强为:
Δp=ρgh=1.0×103kg/m3×10N/kg×0.1m=1000Pa。
答:(1)此时塑料块受到的浮力是50N;
(2)此时绳子的拉力为20N;
(3)绳子剪断前后水对容器底的压强变化了1000Pa。
8.(1)10N-5.2N=4.8N,因此物体浸没在液体中时受到的浮力为4.8N。
(2) 0.48kg÷0.0004m3=1.2×103kg/m3
因此容器内液体的密度为1.2×103kg/m3
(3)液体的体积V液=100cm2×20cm=2000cm3=2×10-3m3,
液体的重力G液=m液g=ρ液V液g=1.2×103kg/ m3×2×10-3m3×10N/kg=24N,
容器对桌面的压力F=(G液+G容器+G物)-F拉=(24N+6N+10N)-5.2N=34.8 N,
受力面积:S=100 cm2=10-2m2,
p==3480Pa。
【解析】【分析】(1)物体所受浮力使弹簧测力计示数减小。
(2)根据阿基米德原理物体所受浮力是排出液体所受重力,求出液体质量,根据密度公式求出液体密度。
(3)先求出物体和容器对桌面的压力,根据公式p=,求出物体浸没时容器对桌面的压强。
9.(1)解: 物体受到的浮力:F浮=G-F拉=8N-6N=2N;
(2)解:
该物体的体积:;
该物体的密度:。
【解析】【分析】(1)根据F浮=G-F拉计算物体受到的浮力;
(2)首先根据计算出物体的体积,再根据计算物体的密度。
10.(1)解:
(2)解:
(3)解:
【解析】【分析】(1)根据F浮=G-F拉计算金属块在水中受到的浮力;
(2)当金属块完全浸没在水中时,它排开水的体积等于自身体积,即 ,据此计算出金属块的体积,再根据 计算出金属块的质量,最后根据 计算出金属块的密度。
(3)首先根据F浮=G-F拉计算出金属块在盐水中受到的浮力,再根据阿基米德原理的变形式 计算出盐水的密度。
11.(1)秤盘上不放物体,始终在水面漂浮,即浮力等于重力,
即F浮力=G=ρ液gV排;
6N=103kg/m3×10N/kg×(0.01m2×h浸);
解得:h浸=0.06m;
(2)当浮力秤上物体的质量最大时,此时小筒和秤盘的总重和物体的重力之和等于此时受到的浮力,
即F浮力'=G总+G;
ρ液gV排'=G总+G;
103kg/m3×10N/kg×(0.01m2×0.2)=6N+m×10N/kg;
解得:m=1.4kg。
【解析】【分析】(1)浮力秤始终在水面漂浮,即浮力等于重力,将阿基米德原理F浮=ρ液gV排代入计算即可;
(2)当浮力秤上物体的质量最大时,小筒浸入的深度为0.2m,此时小筒和秤盘的总重和物体的重力之和等于此时受到的浮力,根据二力平衡的知识计算即可。
12.解:(1)由ρ可知,木块的质量为:
m=ρV=0.6×103kg/m3×1m×1m×2m=1200kg,
木块的重力为:
G=mg=1200kg×10N/kg=1.2×104N;
(2)未注水时,甲中木块对水平池底的压力为:
F=G=1.2×104N,
此时甲中木块对水平池底的压强为:
p6000Pa;
(3)物体漂浮时,浮力等于重力,因此两种放置方式木块受到的浮力相等,由F浮=ρ水gV排可知,木块排开水的体积相等;
(3)木块漂浮时,由F浮=G可得ρ水gV排=ρ木gV,
即V排V1m×1m×2m=1.2m3,
当水池内注水深度达到0.8米时,以乙方式放置,淹没的体积为V排乙=1m×1m×0.8m=0.8m3,
淹没的体积小于木块漂浮的体积,所以乙中木块沉底,乙中木块的浮力为:
F乙=ρ水gV乙=1.0×103kg/m3×10N/kg×0.8m3=8×103N。
答:(1)木块的重力为1.2×104N;
(2)未注水时,甲中木块对水平池底的压强为6000Pa;
(3)=;
(4)当乙水池内注水深度达到0.8米时,乙中木块所受的浮力为8×103N。
13.(1)当h=0时,弹簧测力计的示数为6N,即物体A的重力G=6N,完全浸没在水中:F浮=G-F=6N-2N=4N
(2)完全浸没在水中:
F浮=液gV排
V=V排=
液=1.0103kg/m3
V排===410-4m3=400cm3
V排=sh
物体A的高 h=
(3)根据公式
得m=
因为V=410-4m3
所以== 1.5×103kg/m3
(4)当h=0时,弹簧测力计的示数为6N,即物体A的重力G=6N,完全浸没在水中:F浮=G-F=6N-2.8N=3.2N,
V排=410-4m3
14.解:(1)物体浸没在水中时物体的体积:
V=V排1×10﹣3m3;
(2)物体受到重力、拉力和浮力,物体的重力:G=F浮﹣F=10N﹣4N=6N,
物体的质量:m0.6kg,
物体的密度:ρ0.6×103kg/m3;
(3)物体的密度小于水的密度,将细线剪断后,静止时,漂浮,此时物体受到的浮力:F浮=G=6N,
漂浮时排开水的体积:
V排′6×10﹣4m3,
液面下降的深度为:
Δh0.08m。
答:(1)物体的体积是1×10﹣3m3;
(2)若细绳对物体的拉力为4N,求物体的密度是0.6×103kg/m3;
(3)若剪断细绳,容器液面高度降低了0.08m。
15.(1)解:F浮=G﹣F′=6N﹣4N=2N
(2)解:因物体浸没时排开液体的体积和自身的体积相等,所以,由F浮=ρ水gV排可得,
物体的体积:V=V排= = =2×10﹣4m3,
由G=mg可得,物体的质量:m= = =0.6kg,
物体的密度:ρ= = =3×103kg/m3
(3)解:把木球和物体看做一个整体,受到竖直向上的总浮力和竖直向下的总重力,
因二者悬浮,所以,由力的平衡条件可得:F浮+F浮′=G+G木﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
设木球体积为V,把F浮′=ρ水gV排′和G木=m木g=ρ木Vg代入①式可得:
F浮+ρ水gV=G+ρ木Vg﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②
则木球的体积:V= = =8×10﹣4m3
【解析】【分析】(1)浸没在水中的物体受到竖直向上的浮力和拉力,竖直向下的重力,根据F浮=G-F计算物体受到的浮力;
(2)首先根据 计算出物体的体积,再根据计算出物体的质量,最后根据计算出物体的密度;
(3)将木球和物体看作一个整体,它们在水中悬浮,则它们受到的总浮力等于总重力,据此列出关系式,然后用阿基米德原理 F浮=ρ水gV排 和密度公式将其拆开,代入数据计算出木球的体积。
16.解:
由于冰块漂浮,F浮=G冰,由阿基米原理:F浮=G排;又因为冰熔化前后重力不变,
G冰=G冰化水即有:G排=G冰化水,
因为:F浮=G排=ρ水V排g,G冰=G冰化水=ρ水V冰化水g,
所以:ρ水V排g=ρ水V冰化水g,
故V排=V冰化水
所以冰熔化前后水面不升也不降。
故答案为:(1)不变;(2)见解答部分。
17.(1)物块A浸没在水中受到的浮力F浮=ρ液gV排=103kg/m3×10N/kg×0.2×10-3m3=2N;
(2)弹簧测力计的示数:F2=F拉=G-F浮=2.6N-2N=0.6N;
(3)物块A的密度:。
【解析】【分析】(1)根据阿基米德原理F浮=ρ液gV排计算出物体浸没时受到的浮力;
(2)根据F拉=G-F浮计算出浸没时弹簧测力计的示数F2;
(3)根据公式计算出物体的密度。
18.(1)根据甲乙两图可知,石块在水中受到的浮力:F浮力=G-F拉=4N-3N=1N;
(2)石块的体积;
(3)石块的密度;
(4)根据甲丙两图可知,石块在盐水中受到的浮力:F浮力'=G-F拉'=4N-2.9N=1.1N;
则盐水的密度为:。
【解析】【分析】(1)根据甲乙两图,利用公式F浮力=G-F拉计算出石块在水中受到的浮力;
(2)根据计算石块的体积;
(3)根据公式计算出石块的密度;
(4)根据甲丙两图,利用公式F浮力'=G-F拉'计算出石块在盐水中受到的浮力,再根据计算盐水的密度。
19.(1)由图象知,当h=0时,此时弹簧测力计的示数为18N,圆柱体的重力等于弹簧测力计的示数,则G=18N;
当h≥17cm时,弹簧测力计的示数不变,说明此时浮力不变,圆柱体完全浸没,此时圆柱体受到的拉力F拉=12N;
圆柱体浸没液体时受到的浮力:F浮=G-F拉=18N-12N=6N;
(2)由图知从7cm时弹簧测力计的示数逐渐减小,到17cm弹簧测力计的示数不变,
所以圆柱体额高度为:17cm-7cm=10cm,
圆柱体浸没在液体中,排开液体的体积:V排=V=Sh=40cm2×10cm=400cm3=4×10-4m3,
液体的密度:;
(3)液体的体积:V液=S′h液=100cm2×30cm=3000cm3=3×10-3m3,
液体的质量:m液=ρ液V液=1.5×103kg/m3×3×10-3m3=4.5kg,
将圆柱体、圆筒、液体看做一个整体,
圆筒对地面的压力:F=(m液+m筒)g+G-F拉=(4.5kg+0.5kg)×10N/kg+18N-12N=56N,
受力面积S=100cm2=0.01m2,
圆筒对地面的压强:。
【解析】【分析】(1)根据图象分析出物体的重力、完全浸没时受到的拉力,利用称重法测浮力F浮=G-F拉求圆柱体浸没液体时受到的浮力;
(2)求出了圆柱体浸没液体时受到的浮力,求出圆柱体的体积(浸没时排开液体的体积),利用F浮=ρ液gV排求液体的密度;
(3)此时圆筒对桌面的压力等于圆筒、圆柱体、液体的总重减去圆柱体受到的拉力,知道受力面积大小,利用 求圆筒对桌面的压强。
20.(1)解:∵对图乙中CD段物体受力分析可知:F=G=54N
∴m= = =5.4kg
(2)解:∵对图乙中AB段物体受力分析可知:F浮+F=G
∴F浮=G-F=54N-34N=20N
(3)解:V=V排= = =2×10-3m3
ρ= =2.7×103kg/m3
【解析】【分析】当物体完全浸没水中时,它排开水的体积不变,则它受到的浮力不变,根据F拉=G-F浮可知,此时绳子的拉力不变。当物体开始露出水面时,它排开水的体积变小,则它受到的浮力变小,因此绳子的拉力变大。当物体完全露出水面后,它不再受到浮力,此时绳子的拉力等于重力。
(1)根据图乙确定该物体的重力,然后根据 计算出它的质量。
(2)根据图乙确定该物体完全浸没时绳子的拉力,再根据 F浮=G-F 计算出它受到的最大浮力。
(3)当物体完全浸没时,它排开水的体积等于自身体积,即 ,然后根据 计算出金属块的密度。
21. (1)改变自身重力
(2)解:漂浮时,F浮= G排= m排g=9ⅹ106kgⅹ10N/kg=9×107N
答:核潜艇以水上最大排水量漂浮在海水中时受到的浮力为9×107牛。
(3)解:核潜艇以水下最大排水量悬停在海水中时,F悬浮=G排下=G
排出3000t海水后,核潜艇漂浮在海面上时,F漂浮=G排=G’
则核潜艇前后浮力的减少量为:△F浮=F悬浮-F漂浮=G-G’=△G= Dmg=3ⅹ106kgⅹ10N/kg=3×107N
V露=ΔV排= =3×103m3
【解析】【分析】(1)核潜艇在水中浸没时排开水的体积不变,即它受到的浮力不变,要改变浮沉状态,就只能改变自身重力,即通过调节水仓中海水的重力实现浮沉变化。
(2)根据阿基米德原理F浮=G排=m排g计算出漂浮时受到的浮力;
(3)核潜艇漂浮与悬浮时排开液体的体积不同则所受浮力不同,根据核潜艇悬浮与漂浮时的浮力差,利用阿基米德原理F浮=ρ液gV排计算悬浮与漂浮时排开液体体积的差值,即核潜艇漂浮时露出海面的体积。
22.(1)解:不加液体时,内筒处于漂浮状态,受到的浮力F浮=G桶=m桶g=0.2kg×10N/kg=2N
(2)解:当内筒的18cm刻度与水面相平时,内筒受到的浮力F浮=ρ水gV排=ρ水gSh浸=1.0×103kg/m3×10N/kg×20×10-4m2×0.18m=3.6N
小桶的重力G桶=m桶g=0.2kg×10N/kg=2N
根据漂浮条件可得,小筒内液体的重力G液=F浮-G桶=3.6N-2N=1.6N
小桶内液体的质量m液= = =0.16N
小桶内液体的体积为 V液=Sh液=20×10-4m2×0.1m=2×10-4m3
小桶内液体的密度 ρ= = =0.8×103kg/m3
(2)如果要增大该装置的测量范围,需要让内筒在没有放入液体前浸入水中的体积减小,根据F浮=ρ液gV排知要想使排开液体的体积减小,需要增大外筒中液体的密度;或减小内筒的重力使内筒受到的浮力减小,或减小每次倒入液体的深度使内筒的总重力减小,从而减小浮力。
【解析】【分析】(1)小筒始终在液面漂浮,根据漂浮条件计算出不加液体时小筒受到的浮力;
(2)当内筒的18cm刻度与水面相平时,首先根据阿基米德原理 F浮=ρ水gV排=ρ水gSh浸 计算出此时内筒受到的浮力,然后根据 G桶=m桶g 计算出小桶的重力,接下来根据 G液=F浮-G桶 计算出小桶内液体的重力,利用 计算出液体的质量,最后根据 计算出液体的密度。
(3)根据阿基米德原理F浮=ρ液gV排分析增大测量范围的方法。
同课章节目录
