人教A版高二数学选择性必修第一册1.1 空间向量及其运算 同步精练(含解析)
文档属性
| 名称 | 人教A版高二数学选择性必修第一册1.1 空间向量及其运算 同步精练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 00:00:00 | ||
图片预览




文档简介
本资料分享自高中数学同步资源大全QQ群483122854 专注收集同步资源期待你的加入与分享
人教A版高二数学选择性必修第一册1.1 空间向量及其运算同步精练(原卷版)
【题组一 概念的辨析】
1.(2020·辽宁沈阳.高二期末)在下列结论中:
①若向量共线,则向量所在的直线平行;
②若向量所在的直线为异面直线,则向量一定不共面;
③若三个向量两两共面,则向量共面;
④已知空间的三个向量,则对于空间的任意一个向量总存在实数x,y,z使得.
其中正确结论的个数是( )
A.0 B.1 C.2 D.3
2(2019·全国高二)下列说法中正确的是( )
A.若,则,的长度相等,方向相同或相反
B.若向量是向量的相反向量,则
C.空间向量的减法满足结合律
D.在四边形中,一定有
3.(2020·陕西新城.西安中学高二期末(理))给出下列命题:
①若空间向量满足,则;
②空间任意两个单位向量必相等;
③对于非零向量,由,则;
④在向量的数量积运算中.
其中假命题的个数是( )
A.1 B.2 C.3 D.4
4.(2019·长宁.上海市延安中学高二期中)给出以下结论:
①空间任意两个共起点的向量是共面的;
②两个相等向量就是相等长度的两条有向线段表示的向量;
③空间向量的加法满足结合律:;
④首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.
请将正确的说法题号填在横线上:__________.
【题组二 空间向量的线性运算】
1.(2020·辽宁沈阳.高二期末)如图,在正方体中,点分别是面对角线A1B与B1D1的中点,若=a,=b,=c,则=( )
A. B.
C. D.
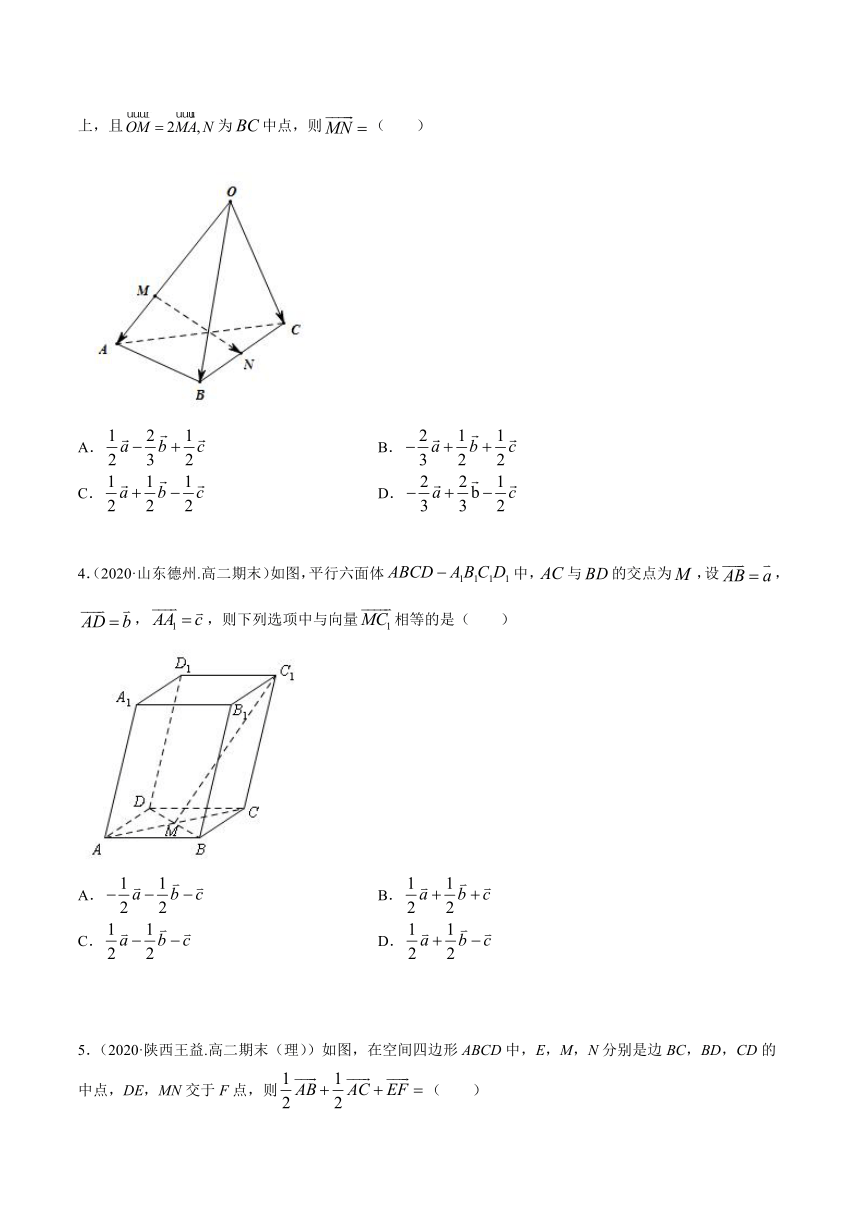
2.(2020·全国高二)在四面体中,点在上,且,为中点,则等于( )
A. B.
C. D.
3(2020·山东章丘四中高二月考)如图所示,在空间四边形中,,点在上,且为中点,则( )
A. B.
C. D.
4.(2020·山东德州.高二期末)如图,平行六面体中,与的交点为,设,,,则下列选项中与向量相等的是( )
A. B.
C. D.
5.(2020·陕西王益.高二期末(理))如图,在空间四边形ABCD中,E,M,N分别是边BC,BD,CD的中点,DE,MN交于F点,则( )
A. B. C. D.
(2019·江苏省苏州实验中学高二月考)平行六面体中,,则实数x,y,z的值分别为( )
A. B. C. D.
7.(2020·湖北黄石.高二期末)如图,已知空间四边形,其对角线为,分别是对边的中点,点在线段上,,现用基向量表示向量,设,则的值分别是( )
A. B.
C. D.
8.(2020·全国高二课时练习)在正方体ABCD-A1B1C1D1中,已知下列各式:①(+)+1;②(+)+;③(+)+;④(+)+.其中运算的结果为的有___个.
9.(2020·江苏省如东高级中学高一月考)在四面体中,、分别是、的中点,若记,,,则______.
(2020·全国高二课时练习)已知正方体ABCD-A1B1C1D1中,若点F是侧面CD1的中心,且则m,n的值分别为( )
A.,- B.-,- C.-, D.,
【题组三 空间向量的共面问题】
1.(2020·涟水县第一中学高二月考)是空间四点,有以下条件:
①; ②;
③; ④,
能使四点一定共面的条件是______
2.(2019·江苏海安高级中学高二期中(理))设空间任意一点和不共线三点,且点满足向量关系,若四点共面,则______.
3.(2020·全国高二课时练习)对于空间任意一点和不共线的三点,,,有如下关系:,则( )
A.四点,,,必共面 B.四点,,,必共面
C.四点,,,必共面 D.五点,,,,必共面
4.(2020·宁阳县第四中学高二期末)对于空间任意一点O和不共线的三点A,B,C,有如下关系:,则( )
A.四点O,A,B,C必共面 B.四点P,A,B,C必共面
C.四点O,P,B,C必共面 D.五点O,P,A,B,C必共面
(2020·四川阆中中学高二月考(理))为空间任意一点,三点不共线,若=,则四点( )
A.一定不共面 B.不一定共面 C.一定共面 D.无法判断
(2019·建瓯市第二中学高二月考)已知、、三点不共线,对平面外的任一点,下列条件中能确定点与点、、一定共面的是( )
A. B.
C. D.
7.(2020·西夏.宁夏育才中学高二期末(理))已知为空间任意一点,若,则四点( )
A.一定不共面 B.一定共面 C.不一定共面 D.无法判断
【题组四 空间向量的数量积】
1.(2020·山东新泰市第一中学高一期中)如图,平行六面体中,,,,则( )
A. B. C. D.
2.(2020·四川遂宁.高三三模(理))如图,平行六面体中,,,,,,则的长为_____.
3.(2020·全国高二课时练习)如图,分别是四面体的棱的中点,是的三等分点.(1)用向量 ,,表示和.(2)若四面体的所有棱长都等于1,求的值.
4..(2020·全国高二课时练习)如图,三棱柱中,底面边长和侧棱长都等于1,.
(1)设,,,用向量,,表示,并求出的长度;
(2)求异面直线与所成角的余弦值.
5.(2020·全国高二课时练习)如图,三棱柱中,底面边长和侧棱长都相等,,则异面直线与所成角的余弦值为_____________
6.如图,已知线段AB⊥平面α,BC α,CD⊥BC,DF⊥平面α,且∠DCF=30°,D与A在α的同侧,若AB=BC=CD=2,求A,D两点间的距离.
人教A版高二数学选择性必修第一册1.1 空间向量及其运算同步精练(解析版)
【题组一 概念的辨析】
1.(2020·辽宁沈阳.高二期末)在下列结论中:
①若向量共线,则向量所在的直线平行;
②若向量所在的直线为异面直线,则向量一定不共面;
③若三个向量两两共面,则向量共面;
④已知空间的三个向量,则对于空间的任意一个向量总存在实数x,y,z使得.
其中正确结论的个数是( )
A.0 B.1 C.2 D.3
【答案】A
【解析】平行向量就是共线向量,它们的方向相同或相反,未必在同一条直线上,故①错.
两条异面直线的方向向量可通过平移使得它们在同一平面内,故②错,
三个向量两两共面,这三个向量未必共面,如三棱锥中,两两共面,但它们不是共面向量,故③错.根据空间向量基本定理,需不共面,故④错.综上,选A.
2(2019·全国高二)下列说法中正确的是( )
A.若,则,的长度相等,方向相同或相反
B.若向量是向量的相反向量,则
C.空间向量的减法满足结合律
D.在四边形中,一定有
【答案】B
【解析】对于A,向量的模相等指的是向量的长度相等,方向具有不确定性,因而不一定方向相同或相反,所以A错误.对于B,相反向量指的是大小相等,方向相反的两个向量.因而相反向量满足模长相等,所以B正确.
对于C,减法结合律指的是,因而由运算可得空间向量减法不满足结合律.所以C错误.对于D满足的一定是平行四边形,一般四边形是不满足的,因而D错误.
综上可知,正确的为B,故选:B
3.(2020·陕西新城.西安中学高二期末(理))给出下列命题:
①若空间向量满足,则;
②空间任意两个单位向量必相等;
③对于非零向量,由,则;
④在向量的数量积运算中.
其中假命题的个数是( )
A.1 B.2 C.3 D.4
【答案】D
【解析】对于①,空间向量的方向不一定相同,即不一定成立,故①错误;
对于②,单位向量的方向不一定相同,故②错误;
对于③,取,,,满足,且,但是,故③错误;对于④,因为和都是常数,所以和表示两个向量,若和方向不同
则和不相等,故④错误.故选:D.
4.(2019·长宁.上海市延安中学高二期中)给出以下结论:
①空间任意两个共起点的向量是共面的;
②两个相等向量就是相等长度的两条有向线段表示的向量;
③空间向量的加法满足结合律:;
④首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.
请将正确的说法题号填在横线上:__________.
【答案】①③④
【解析】①中,两个向量共起点,与两向量终点共有个点,则点共面,可知两向量共面,①正确;
②中,两个相等向量需大小相等,方向相同,②错误;
③中,空间向量加法满足结合律,③正确;
④中,由向量加法的三角形法则可知④正确.
故答案为:①③④
【题组二 空间向量的线性运算】
1.(2020·辽宁沈阳.高二期末)如图,在正方体中,点分别是面对角线A1B与B1D1的中点,若=a,=b,=c,则=( )
A. B.
C. D.
【答案】D
【解析】根据向量的线性运算
所以选D
2.(2020·全国高二)在四面体中,点在上,且,为中点,则等于( )
A. B.
C. D.
【答案】B
【解析】.故选:B
3(2020·山东章丘四中高二月考)如图所示,在空间四边形中,,点在上,且为中点,则( )
A. B.
C. D.
【答案】B
【解析】由向量的加法和减法运算:.
故选:B
4.(2020·山东德州.高二期末)如图,平行六面体中,与的交点为,设,,,则下列选项中与向量相等的是( )
A. B.
C. D.
【答案】B
【解析】如图所示,,
,,,,,
,
故选:.
5.(2020·陕西王益.高二期末(理))如图,在空间四边形ABCD中,E,M,N分别是边BC,BD,CD的中点,DE,MN交于F点,则( )
A. B. C. D.
【答案】B
【解析】是边的中点,;;
故选:.
6.(2019·江苏省苏州实验中学高二月考)平行六面体中,,则实数x,y,z的值分别为( )
A. B. C. D.
【答案】C
【解析】
,.故选:C.
7.(2020·湖北黄石.高二期末)如图,已知空间四边形,其对角线为,分别是对边的中点,点在线段上,,现用基向量表示向量,设,则的值分别是( )
A. B.
C. D.
【答案】D
【解析】
,,故选:
8.(2020·全国高二课时练习)在正方体ABCD-A1B1C1D1中,已知下列各式:①(+)+1;②(+)+;③(+)+;④(+)+.其中运算的结果为的有___个.
【答案】4
【解析】根据空间向量的加法运算以及正方体的性质逐一进行判断:
①(+)+=+=;
②(+)+=+=;
③(+)+=+=;
④(+)+=+=.
所以4个式子的运算结果都是.
故答案为:4.
9.(2020·江苏省如东高级中学高一月考)在四面体中,、分别是、的中点,若记,,,则______.
【答案】
【解析】在四面体中,、分别是、的中点,
则
.故答案为:.
10.(2020·全国高二课时练习)已知正方体ABCD-A1B1C1D1中,若点F是侧面CD1的中心,且则m,n的值分别为( )
A.,- B.-,- C.-, D.,
【答案】A
【解析】由于,所以.故选:A
【题组三 空间向量的共面问题】
1.(2020·涟水县第一中学高二月考)是空间四点,有以下条件:
①; ②;
③; ④,
能使四点一定共面的条件是______
【答案】④
【解析】对于④,,由空间向量共面定理可知四点一定共面,①②③不满足共面定理的条件.故答案为:④
2.(2019·江苏海安高级中学高二期中(理))设空间任意一点和不共线三点,且点满足向量关系,若四点共面,则______.
【答案】
【解析】因为四点共面,三点不共线,
所以
因为,
因为是任意一点,故可不共面,所以,
故.故答案为:1
3.(2020·全国高二课时练习)对于空间任意一点和不共线的三点,,,有如下关系:,则( )
A.四点,,,必共面 B.四点,,,必共面
C.四点,,,必共面 D.五点,,,,必共面
【答案】B
【解析】因为,所以,
即,根据共面向量基本定理,可得,,共面,
所以,,,,四点共面.故选:B.
4.(2020·宁阳县第四中学高二期末)对于空间任意一点O和不共线的三点A,B,C,有如下关系:,则( )
A.四点O,A,B,C必共面 B.四点P,A,B,C必共面
C.四点O,P,B,C必共面 D.五点O,P,A,B,C必共面
【答案】B
【解析】由已知得,而,四点、、、共面.
故选:.
5.(2020·四川阆中中学高二月考(理))为空间任意一点,三点不共线,若=,则四点( )
A.一定不共面 B.不一定共面
C.一定共面 D.无法判断
【答案】C
【解析】因为=,且,所以四点共面.
6.(2019·建瓯市第二中学高二月考)已知、、三点不共线,对平面外的任一点,下列条件中能确定点与点、、一定共面的是( )
A. B.
C. D.
【答案】B
【解析】若,
故可得
即,
则,
故
整理得
又因为共面,
故可得共面,而其它选项不符合,
即可得四点共面.
故选:B.
7.(2020·西夏.宁夏育才中学高二期末(理))已知为空间任意一点,若,则四点( )
A.一定不共面 B.一定共面 C.不一定共面 D.无法判断
【答案】B
【解析】由若 ,当且仅当 时, 四点共面.
,
而 故 四点共面,故选B
【题组四 空间向量的数量积】
1.(2020·山东新泰市第一中学高一期中)如图,平行六面体中,,,,则( )
A. B. C. D.
【答案】D
【解析】,
,.故选:D
2.(2020·四川遂宁.高三三模(理))如图,平行六面体中,,,,,,则的长为_____.
【答案】
【解析】平行六面体中,
,,,,,
,
.
.故答案为:.
3.(2020·全国高二课时练习)如图,分别是四面体的棱的中点,是的三等分点.
(1)用向量 ,,表示和.
(2)若四面体的所有棱长都等于1,求的值.
【答案】(1),(2).
【解析】(1),
∴
(2)四面体的所有棱长都等于1,各面为等边三角形, ,,
4..(2020·全国高二课时练习)如图,三棱柱中,底面边长和侧棱长都等于1,.
(1)设,,,用向量,,表示,并求出的长度;
(2)求异面直线与所成角的余弦值.
【答案】(1);;(2).
【解析】
解:(1),
又,
同理可得,
则.
(2)因为,
所以,
因为,
所以.
则异面直线与所成角的余弦值为.
5.(2020·全国高二课时练习)如图,三棱柱中,底面边长和侧棱长都相等,,则异面直线与所成角的余弦值为_____________
【答案】
【解析】三棱柱中,底面边长和侧棱长都相等,,设棱长为1,
则,,
.
又,,
所以
而,
,
所以.
故答案为:.
6.如图3 1 22所示,在空间四边形OABC中,OA,OB,OC两两成60°角,且OA=OB=OC=2,E为OA的中点,F为BC的中点,试求E,F间的距离.
图3 1 22
【答案】
【解析】=+=+(+)=+[(-)+(-)]=-++,
所以=2+2+2+2××·+2××·+2××·=2.
∴||=,即E,F间的距离为.
7.如图,已知线段AB⊥平面α,BC α,CD⊥BC,DF⊥平面α,且∠DCF=30°,D与A在α的同侧,若AB=BC=CD=2,求A,D两点间的距离.
【答案】2
【解析】∵=++,
∴||2=(++)2=||2+||2+||2+2·+2·+2·=12+2(2·2·cos90°+2·2·cos120°+2·2·cos90°)=8,
∴||=2,即A,D两点间的距离为2.
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
人教A版高二数学选择性必修第一册1.1 空间向量及其运算同步精练(原卷版)
【题组一 概念的辨析】
1.(2020·辽宁沈阳.高二期末)在下列结论中:
①若向量共线,则向量所在的直线平行;
②若向量所在的直线为异面直线,则向量一定不共面;
③若三个向量两两共面,则向量共面;
④已知空间的三个向量,则对于空间的任意一个向量总存在实数x,y,z使得.
其中正确结论的个数是( )
A.0 B.1 C.2 D.3
2(2019·全国高二)下列说法中正确的是( )
A.若,则,的长度相等,方向相同或相反
B.若向量是向量的相反向量,则
C.空间向量的减法满足结合律
D.在四边形中,一定有
3.(2020·陕西新城.西安中学高二期末(理))给出下列命题:
①若空间向量满足,则;
②空间任意两个单位向量必相等;
③对于非零向量,由,则;
④在向量的数量积运算中.
其中假命题的个数是( )
A.1 B.2 C.3 D.4
4.(2019·长宁.上海市延安中学高二期中)给出以下结论:
①空间任意两个共起点的向量是共面的;
②两个相等向量就是相等长度的两条有向线段表示的向量;
③空间向量的加法满足结合律:;
④首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.
请将正确的说法题号填在横线上:__________.
【题组二 空间向量的线性运算】
1.(2020·辽宁沈阳.高二期末)如图,在正方体中,点分别是面对角线A1B与B1D1的中点,若=a,=b,=c,则=( )
A. B.
C. D.
2.(2020·全国高二)在四面体中,点在上,且,为中点,则等于( )
A. B.
C. D.
3(2020·山东章丘四中高二月考)如图所示,在空间四边形中,,点在上,且为中点,则( )
A. B.
C. D.
4.(2020·山东德州.高二期末)如图,平行六面体中,与的交点为,设,,,则下列选项中与向量相等的是( )
A. B.
C. D.
5.(2020·陕西王益.高二期末(理))如图,在空间四边形ABCD中,E,M,N分别是边BC,BD,CD的中点,DE,MN交于F点,则( )
A. B. C. D.
(2019·江苏省苏州实验中学高二月考)平行六面体中,,则实数x,y,z的值分别为( )
A. B. C. D.
7.(2020·湖北黄石.高二期末)如图,已知空间四边形,其对角线为,分别是对边的中点,点在线段上,,现用基向量表示向量,设,则的值分别是( )
A. B.
C. D.
8.(2020·全国高二课时练习)在正方体ABCD-A1B1C1D1中,已知下列各式:①(+)+1;②(+)+;③(+)+;④(+)+.其中运算的结果为的有___个.
9.(2020·江苏省如东高级中学高一月考)在四面体中,、分别是、的中点,若记,,,则______.
(2020·全国高二课时练习)已知正方体ABCD-A1B1C1D1中,若点F是侧面CD1的中心,且则m,n的值分别为( )
A.,- B.-,- C.-, D.,
【题组三 空间向量的共面问题】
1.(2020·涟水县第一中学高二月考)是空间四点,有以下条件:
①; ②;
③; ④,
能使四点一定共面的条件是______
2.(2019·江苏海安高级中学高二期中(理))设空间任意一点和不共线三点,且点满足向量关系,若四点共面,则______.
3.(2020·全国高二课时练习)对于空间任意一点和不共线的三点,,,有如下关系:,则( )
A.四点,,,必共面 B.四点,,,必共面
C.四点,,,必共面 D.五点,,,,必共面
4.(2020·宁阳县第四中学高二期末)对于空间任意一点O和不共线的三点A,B,C,有如下关系:,则( )
A.四点O,A,B,C必共面 B.四点P,A,B,C必共面
C.四点O,P,B,C必共面 D.五点O,P,A,B,C必共面
(2020·四川阆中中学高二月考(理))为空间任意一点,三点不共线,若=,则四点( )
A.一定不共面 B.不一定共面 C.一定共面 D.无法判断
(2019·建瓯市第二中学高二月考)已知、、三点不共线,对平面外的任一点,下列条件中能确定点与点、、一定共面的是( )
A. B.
C. D.
7.(2020·西夏.宁夏育才中学高二期末(理))已知为空间任意一点,若,则四点( )
A.一定不共面 B.一定共面 C.不一定共面 D.无法判断
【题组四 空间向量的数量积】
1.(2020·山东新泰市第一中学高一期中)如图,平行六面体中,,,,则( )
A. B. C. D.
2.(2020·四川遂宁.高三三模(理))如图,平行六面体中,,,,,,则的长为_____.
3.(2020·全国高二课时练习)如图,分别是四面体的棱的中点,是的三等分点.(1)用向量 ,,表示和.(2)若四面体的所有棱长都等于1,求的值.
4..(2020·全国高二课时练习)如图,三棱柱中,底面边长和侧棱长都等于1,.
(1)设,,,用向量,,表示,并求出的长度;
(2)求异面直线与所成角的余弦值.
5.(2020·全国高二课时练习)如图,三棱柱中,底面边长和侧棱长都相等,,则异面直线与所成角的余弦值为_____________
6.如图,已知线段AB⊥平面α,BC α,CD⊥BC,DF⊥平面α,且∠DCF=30°,D与A在α的同侧,若AB=BC=CD=2,求A,D两点间的距离.
人教A版高二数学选择性必修第一册1.1 空间向量及其运算同步精练(解析版)
【题组一 概念的辨析】
1.(2020·辽宁沈阳.高二期末)在下列结论中:
①若向量共线,则向量所在的直线平行;
②若向量所在的直线为异面直线,则向量一定不共面;
③若三个向量两两共面,则向量共面;
④已知空间的三个向量,则对于空间的任意一个向量总存在实数x,y,z使得.
其中正确结论的个数是( )
A.0 B.1 C.2 D.3
【答案】A
【解析】平行向量就是共线向量,它们的方向相同或相反,未必在同一条直线上,故①错.
两条异面直线的方向向量可通过平移使得它们在同一平面内,故②错,
三个向量两两共面,这三个向量未必共面,如三棱锥中,两两共面,但它们不是共面向量,故③错.根据空间向量基本定理,需不共面,故④错.综上,选A.
2(2019·全国高二)下列说法中正确的是( )
A.若,则,的长度相等,方向相同或相反
B.若向量是向量的相反向量,则
C.空间向量的减法满足结合律
D.在四边形中,一定有
【答案】B
【解析】对于A,向量的模相等指的是向量的长度相等,方向具有不确定性,因而不一定方向相同或相反,所以A错误.对于B,相反向量指的是大小相等,方向相反的两个向量.因而相反向量满足模长相等,所以B正确.
对于C,减法结合律指的是,因而由运算可得空间向量减法不满足结合律.所以C错误.对于D满足的一定是平行四边形,一般四边形是不满足的,因而D错误.
综上可知,正确的为B,故选:B
3.(2020·陕西新城.西安中学高二期末(理))给出下列命题:
①若空间向量满足,则;
②空间任意两个单位向量必相等;
③对于非零向量,由,则;
④在向量的数量积运算中.
其中假命题的个数是( )
A.1 B.2 C.3 D.4
【答案】D
【解析】对于①,空间向量的方向不一定相同,即不一定成立,故①错误;
对于②,单位向量的方向不一定相同,故②错误;
对于③,取,,,满足,且,但是,故③错误;对于④,因为和都是常数,所以和表示两个向量,若和方向不同
则和不相等,故④错误.故选:D.
4.(2019·长宁.上海市延安中学高二期中)给出以下结论:
①空间任意两个共起点的向量是共面的;
②两个相等向量就是相等长度的两条有向线段表示的向量;
③空间向量的加法满足结合律:;
④首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.
请将正确的说法题号填在横线上:__________.
【答案】①③④
【解析】①中,两个向量共起点,与两向量终点共有个点,则点共面,可知两向量共面,①正确;
②中,两个相等向量需大小相等,方向相同,②错误;
③中,空间向量加法满足结合律,③正确;
④中,由向量加法的三角形法则可知④正确.
故答案为:①③④
【题组二 空间向量的线性运算】
1.(2020·辽宁沈阳.高二期末)如图,在正方体中,点分别是面对角线A1B与B1D1的中点,若=a,=b,=c,则=( )
A. B.
C. D.
【答案】D
【解析】根据向量的线性运算
所以选D
2.(2020·全国高二)在四面体中,点在上,且,为中点,则等于( )
A. B.
C. D.
【答案】B
【解析】.故选:B
3(2020·山东章丘四中高二月考)如图所示,在空间四边形中,,点在上,且为中点,则( )
A. B.
C. D.
【答案】B
【解析】由向量的加法和减法运算:.
故选:B
4.(2020·山东德州.高二期末)如图,平行六面体中,与的交点为,设,,,则下列选项中与向量相等的是( )
A. B.
C. D.
【答案】B
【解析】如图所示,,
,,,,,
,
故选:.
5.(2020·陕西王益.高二期末(理))如图,在空间四边形ABCD中,E,M,N分别是边BC,BD,CD的中点,DE,MN交于F点,则( )
A. B. C. D.
【答案】B
【解析】是边的中点,;;
故选:.
6.(2019·江苏省苏州实验中学高二月考)平行六面体中,,则实数x,y,z的值分别为( )
A. B. C. D.
【答案】C
【解析】
,.故选:C.
7.(2020·湖北黄石.高二期末)如图,已知空间四边形,其对角线为,分别是对边的中点,点在线段上,,现用基向量表示向量,设,则的值分别是( )
A. B.
C. D.
【答案】D
【解析】
,,故选:
8.(2020·全国高二课时练习)在正方体ABCD-A1B1C1D1中,已知下列各式:①(+)+1;②(+)+;③(+)+;④(+)+.其中运算的结果为的有___个.
【答案】4
【解析】根据空间向量的加法运算以及正方体的性质逐一进行判断:
①(+)+=+=;
②(+)+=+=;
③(+)+=+=;
④(+)+=+=.
所以4个式子的运算结果都是.
故答案为:4.
9.(2020·江苏省如东高级中学高一月考)在四面体中,、分别是、的中点,若记,,,则______.
【答案】
【解析】在四面体中,、分别是、的中点,
则
.故答案为:.
10.(2020·全国高二课时练习)已知正方体ABCD-A1B1C1D1中,若点F是侧面CD1的中心,且则m,n的值分别为( )
A.,- B.-,- C.-, D.,
【答案】A
【解析】由于,所以.故选:A
【题组三 空间向量的共面问题】
1.(2020·涟水县第一中学高二月考)是空间四点,有以下条件:
①; ②;
③; ④,
能使四点一定共面的条件是______
【答案】④
【解析】对于④,,由空间向量共面定理可知四点一定共面,①②③不满足共面定理的条件.故答案为:④
2.(2019·江苏海安高级中学高二期中(理))设空间任意一点和不共线三点,且点满足向量关系,若四点共面,则______.
【答案】
【解析】因为四点共面,三点不共线,
所以
因为,
因为是任意一点,故可不共面,所以,
故.故答案为:1
3.(2020·全国高二课时练习)对于空间任意一点和不共线的三点,,,有如下关系:,则( )
A.四点,,,必共面 B.四点,,,必共面
C.四点,,,必共面 D.五点,,,,必共面
【答案】B
【解析】因为,所以,
即,根据共面向量基本定理,可得,,共面,
所以,,,,四点共面.故选:B.
4.(2020·宁阳县第四中学高二期末)对于空间任意一点O和不共线的三点A,B,C,有如下关系:,则( )
A.四点O,A,B,C必共面 B.四点P,A,B,C必共面
C.四点O,P,B,C必共面 D.五点O,P,A,B,C必共面
【答案】B
【解析】由已知得,而,四点、、、共面.
故选:.
5.(2020·四川阆中中学高二月考(理))为空间任意一点,三点不共线,若=,则四点( )
A.一定不共面 B.不一定共面
C.一定共面 D.无法判断
【答案】C
【解析】因为=,且,所以四点共面.
6.(2019·建瓯市第二中学高二月考)已知、、三点不共线,对平面外的任一点,下列条件中能确定点与点、、一定共面的是( )
A. B.
C. D.
【答案】B
【解析】若,
故可得
即,
则,
故
整理得
又因为共面,
故可得共面,而其它选项不符合,
即可得四点共面.
故选:B.
7.(2020·西夏.宁夏育才中学高二期末(理))已知为空间任意一点,若,则四点( )
A.一定不共面 B.一定共面 C.不一定共面 D.无法判断
【答案】B
【解析】由若 ,当且仅当 时, 四点共面.
,
而 故 四点共面,故选B
【题组四 空间向量的数量积】
1.(2020·山东新泰市第一中学高一期中)如图,平行六面体中,,,,则( )
A. B. C. D.
【答案】D
【解析】,
,.故选:D
2.(2020·四川遂宁.高三三模(理))如图,平行六面体中,,,,,,则的长为_____.
【答案】
【解析】平行六面体中,
,,,,,
,
.
.故答案为:.
3.(2020·全国高二课时练习)如图,分别是四面体的棱的中点,是的三等分点.
(1)用向量 ,,表示和.
(2)若四面体的所有棱长都等于1,求的值.
【答案】(1),(2).
【解析】(1),
∴
(2)四面体的所有棱长都等于1,各面为等边三角形, ,,
4..(2020·全国高二课时练习)如图,三棱柱中,底面边长和侧棱长都等于1,.
(1)设,,,用向量,,表示,并求出的长度;
(2)求异面直线与所成角的余弦值.
【答案】(1);;(2).
【解析】
解:(1),
又,
同理可得,
则.
(2)因为,
所以,
因为,
所以.
则异面直线与所成角的余弦值为.
5.(2020·全国高二课时练习)如图,三棱柱中,底面边长和侧棱长都相等,,则异面直线与所成角的余弦值为_____________
【答案】
【解析】三棱柱中,底面边长和侧棱长都相等,,设棱长为1,
则,,
.
又,,
所以
而,
,
所以.
故答案为:.
6.如图3 1 22所示,在空间四边形OABC中,OA,OB,OC两两成60°角,且OA=OB=OC=2,E为OA的中点,F为BC的中点,试求E,F间的距离.
图3 1 22
【答案】
【解析】=+=+(+)=+[(-)+(-)]=-++,
所以=2+2+2+2××·+2××·+2××·=2.
∴||=,即E,F间的距离为.
7.如图,已知线段AB⊥平面α,BC α,CD⊥BC,DF⊥平面α,且∠DCF=30°,D与A在α的同侧,若AB=BC=CD=2,求A,D两点间的距离.
【答案】2
【解析】∵=++,
∴||2=(++)2=||2+||2+||2+2·+2·+2·=12+2(2·2·cos90°+2·2·cos120°+2·2·cos90°)=8,
∴||=2,即A,D两点间的距离为2.
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
