人教A版高二数学选择性必修第一册1.3 空间向量及其坐标的运算 同步精练(含解析)
文档属性
| 名称 | 人教A版高二数学选择性必修第一册1.3 空间向量及其坐标的运算 同步精练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 567.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 08:53:03 | ||
图片预览



文档简介
本资料分享自高中数学同步资源大全QQ群483122854 专注收集同步资源期待你的加入与分享
人教A版高二数学选择性必修第一册1.3 空间向量及其坐标的运算同步精练(原卷版)
【题组一 空间向量的坐标运算】
1.(2020·全国高二)已知点,向量,则点坐标是( )
A. B. C. D.
2.(2019·浙江高二学业考试)设点.若,则点B的坐标为( )
A. B. C. D.
3.(2020·绵竹市南轩中学高二月考(理))若,,,则的值为( )
A. B.5 C.7 D.36
4.(2019·包头市第四中学高二期中(理))若直线的方向向量为,平面的法向量为,则可能使的是( )
A., B.,
C., D.,
5.(2020·南京市秦淮中学高二期末)对于任意非零向量,,以下说法错误的有( )
A.若,则
B.若,则
C.
D.若,则为单位向量
6(2020·江苏连云港 高二期末)已知点P是△ABC所在的平面外一点,若=(﹣2,1,4),=(1,﹣2,1),=(4,2,0),则( )
A.AP⊥AB B.AP⊥ BP C.BC= D.AP// BC
7(2020·全国高二课时练习)已知向量.
(1)计算和.
(2)求.
8.(2020·吴起高级中学高二月考(理))已知空间三点,设.
(1)的夹角的余弦值;
(2)若向量互相垂直,求实数的值;
(3)若向量共线,求实数的值.
【题组二 坐标运算在几何中的运用】
1.(2020·全国高二课时练习)棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别是DD1,BD,BB1的中点.
(1)求证:EF⊥CF;
(2)求与所成角的余弦值;
(3)求CE的长.
2.(2019·全国高二)棱长为1的正方体中,,,分别是,,的中点.
(1)求证:;
(2)求与所成角的余弦值;
(3)求的长.
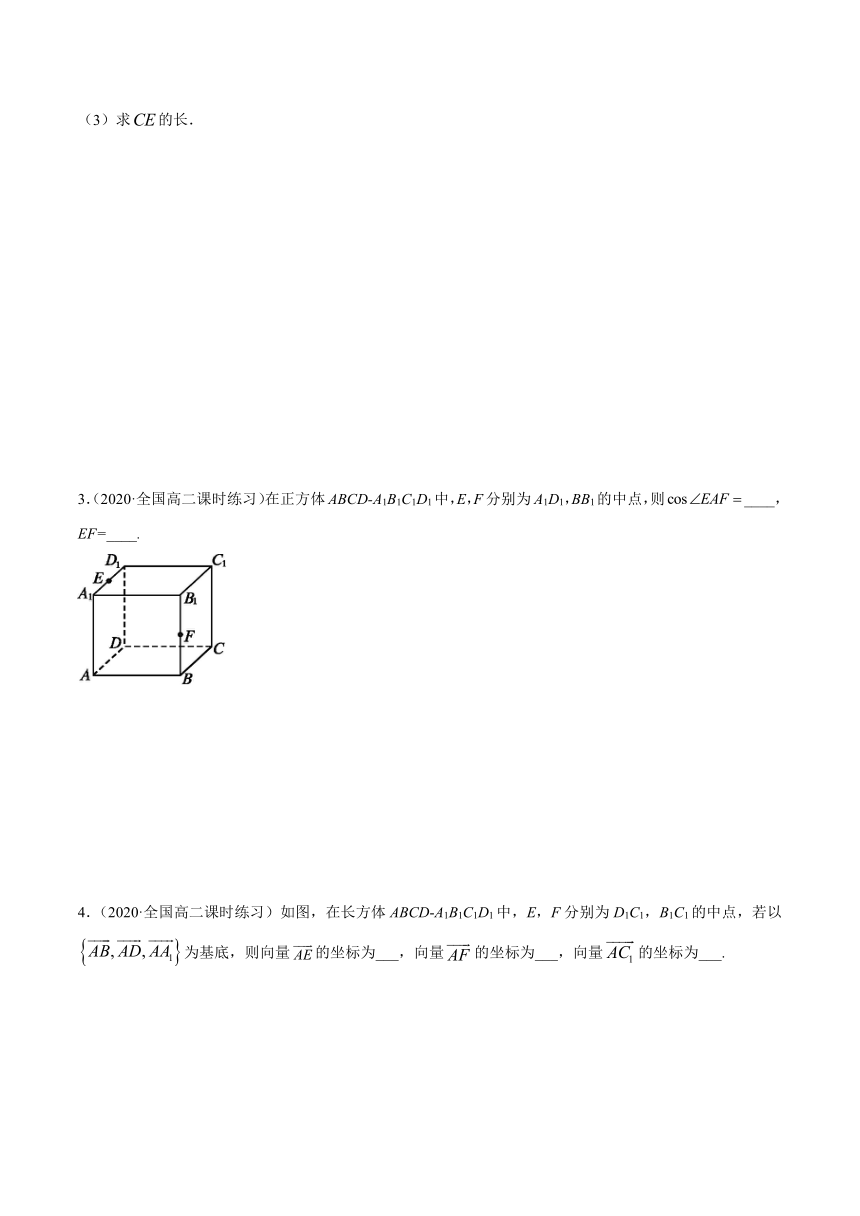
3.(2020·全国高二课时练习)在正方体ABCD-A1B1C1D1中,E,F分别为A1D1,BB1的中点,则____,EF=____.
4.(2020·全国高二课时练习)如图,在长方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,若以为基底,则向量的坐标为___,向量的坐标为___,向量的坐标为___.
【题组三 最值问题】
1.(2019·全国高一课时练习)在平面内的直线上求一点,使点到点的距离最小,并求出此最小值.
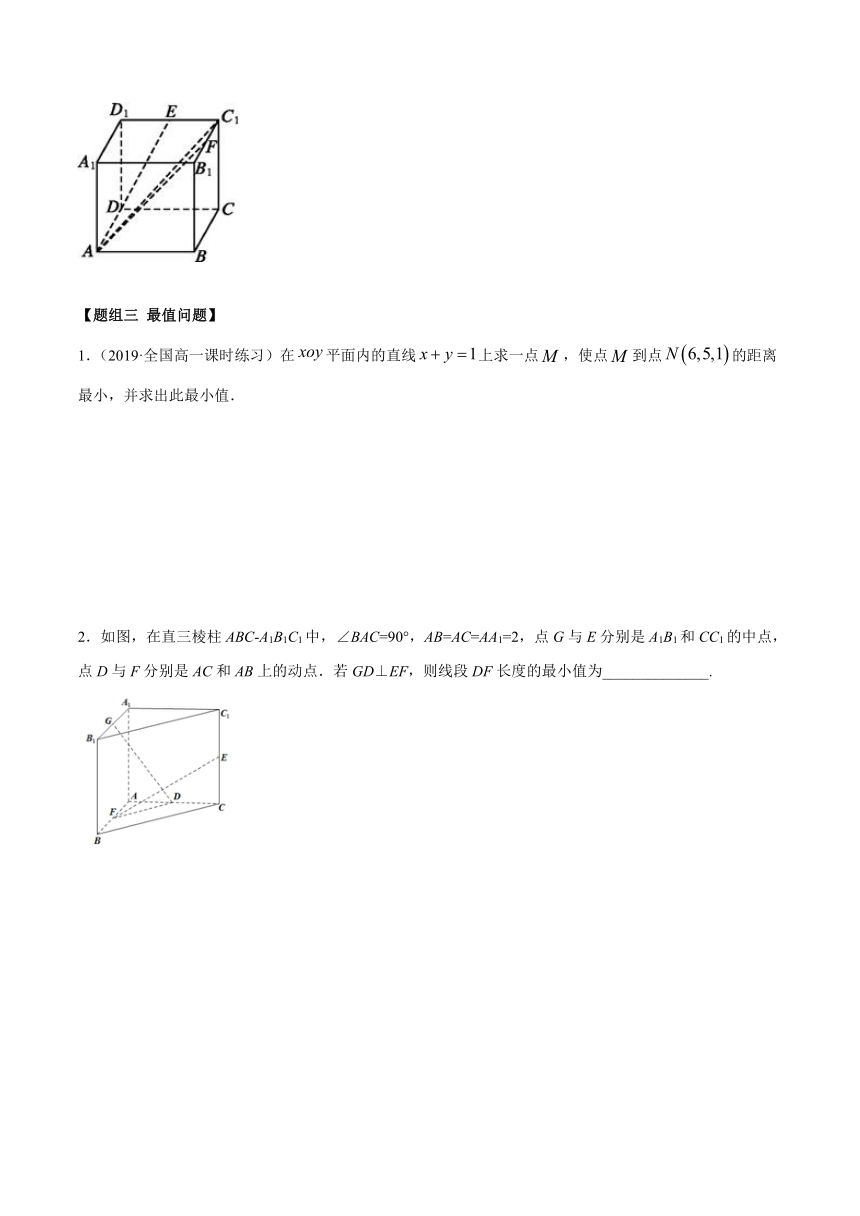
2.如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,点G与E分别是A1B1和CC1的中点,点D与F分别是AC和AB上的动点.若GD⊥EF,则线段DF长度的最小值为______________.
人教A版高二数学选择性必修第一册1.3 空间向量及其坐标的运算同步精练(解析版)
【题组一 空间向量的坐标运算】
1.(2020·全国高二)已知点,向量,则点坐标是( )
A. B. C. D.
【答案】D
【解析】设点,则向量,
所以,所以点.故选:D
2.(2019·浙江高二学业考试)设点.若,则点B的坐标为( )
A. B. C. D.
【答案】C
【解析】设点B的坐标为,则,
∵,∴,解得,故选:C.
3.(2020·绵竹市南轩中学高二月考(理))若,,,则的值为( )
A. B.5 C.7 D.36
【答案】B
【解析】,.
故选:B
4.(2019·包头市第四中学高二期中(理))若直线的方向向量为,平面的法向量为,则可能使的是( )
A., B.,
C., D.,
【答案】D
【解析】A中,所以排除A;B中,所以排除B;
C中,所以排除C;D中,所以,能使.
故选D
5.(2020·南京市秦淮中学高二期末)对于任意非零向量,,以下说法错误的有( )
A.若,则
B.若,则
C.
D.若,则为单位向量
【答案】BD
【解析】对于A选项,因为,则,A选项正确;
对于B选项,若,且,,若,但分式无意义,B选项错误;
对于C选项,由空间向量数量积的坐标运算可知,C选项正确;
对于D选项,若,则,此时,不是单位向量,D选项错误.
故选:BD.
6(2020·江苏连云港 高二期末)已知点P是△ABC所在的平面外一点,若=(﹣2,1,4),=(1,﹣2,1),=(4,2,0),则( )
A.AP⊥AB B.AP⊥ BP C.BC= D.AP// BC
【答案】AC
【解析】因为,故A正确;,,故B不正确;,,故C正确;,,各个对应分量的比例不同,故D不正确。故选:AC。
7(2020·全国高二课时练习)已知向量.
(1)计算和.
(2)求.
【答案】(1);;(2).
【解析】(1)因为向量
所以,
所以
(2)因为,所以
8.(2020·吴起高级中学高二月考(理))已知空间三点,设.
(1)的夹角的余弦值;
(2)若向量互相垂直,求实数的值;
(3)若向量共线,求实数的值.
【答案】(1);(2)或;(3)或.
【解析】(1)已知空间三点,
(2)若向量互相垂直,
又,则
解得:或
(3)向量共线,又
当时,
当时,,成立,
当时,,不成立,
故:或
【题组二 坐标运算在几何中的运用】
1.(2020·全国高二课时练习)棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别是DD1,BD,BB1的中点.
(1)求证:EF⊥CF;
(2)求与所成角的余弦值;
(3)求CE的长.
【答案】(1)证明见解析;(2);(3).
【解析】建立如图所示的空间直角坐标系Dxyz
则
所以
(1)证明:因为,所以,即EF⊥CF.
(2)因为
.
(3)
2.(2019·全国高二)棱长为1的正方体中,,,分别是,,的中点.
(1)求证:;
(2)求与所成角的余弦值;
(3)求的长.
【答案】(1)详见解析;(2);(3).
【解析】建立如图所示的空间直角坐标系
则,,,,.
所以,
,,.
(1)证明:因为
所以
即
(2)因为
由向量夹角的求法可得
∴
(3)根据空间中两点的距离公式可得
.
3.(2020·全国高二课时练习)在正方体ABCD-A1B1C1D1中,E,F分别为A1D1,BB1的中点,则____,EF=____.
【答案】
【解析】以A为原点,AB,AD,AA1分别为x轴、y轴、z轴建立直角坐标系
设正方体棱长为1,则
.
故答案为:;
4.(2020·全国高二课时练习)如图,在长方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,若以为基底,则向量的坐标为___,向量的坐标为___,向量的坐标为___.
【答案】
【解析】因为,所以向量的坐标为.
因为,
所以向量的坐标为.
因为,所以向量的坐标为.
故答案为:;;
【题组三 最值问题】
1.(2019·全国高一课时练习)在平面内的直线上求一点,使点到点的距离最小,并求出此最小值.
【答案】点的坐标为时,
【解析】设,
则.
所以当,即点的坐标为时,.
2.如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,点G与E分别是A1B1和CC1的中点,点D与F分别是AC和AB上的动点.若GD⊥EF,则线段DF长度的最小值为______________.
【答案】
【解析】建立如图所示的空间直角坐标系,则A(0,0,0),E(0,2,1),G(1,0,2),设F(x,0,0),D(0,y,0),
则,,
由于GD⊥EF,所以,
所以,
故,
所以当时,线段DF长度取得最小值,且最小值为.
故答案为:
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
人教A版高二数学选择性必修第一册1.3 空间向量及其坐标的运算同步精练(原卷版)
【题组一 空间向量的坐标运算】
1.(2020·全国高二)已知点,向量,则点坐标是( )
A. B. C. D.
2.(2019·浙江高二学业考试)设点.若,则点B的坐标为( )
A. B. C. D.
3.(2020·绵竹市南轩中学高二月考(理))若,,,则的值为( )
A. B.5 C.7 D.36
4.(2019·包头市第四中学高二期中(理))若直线的方向向量为,平面的法向量为,则可能使的是( )
A., B.,
C., D.,
5.(2020·南京市秦淮中学高二期末)对于任意非零向量,,以下说法错误的有( )
A.若,则
B.若,则
C.
D.若,则为单位向量
6(2020·江苏连云港 高二期末)已知点P是△ABC所在的平面外一点,若=(﹣2,1,4),=(1,﹣2,1),=(4,2,0),则( )
A.AP⊥AB B.AP⊥ BP C.BC= D.AP// BC
7(2020·全国高二课时练习)已知向量.
(1)计算和.
(2)求.
8.(2020·吴起高级中学高二月考(理))已知空间三点,设.
(1)的夹角的余弦值;
(2)若向量互相垂直,求实数的值;
(3)若向量共线,求实数的值.
【题组二 坐标运算在几何中的运用】
1.(2020·全国高二课时练习)棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别是DD1,BD,BB1的中点.
(1)求证:EF⊥CF;
(2)求与所成角的余弦值;
(3)求CE的长.
2.(2019·全国高二)棱长为1的正方体中,,,分别是,,的中点.
(1)求证:;
(2)求与所成角的余弦值;
(3)求的长.
3.(2020·全国高二课时练习)在正方体ABCD-A1B1C1D1中,E,F分别为A1D1,BB1的中点,则____,EF=____.
4.(2020·全国高二课时练习)如图,在长方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,若以为基底,则向量的坐标为___,向量的坐标为___,向量的坐标为___.
【题组三 最值问题】
1.(2019·全国高一课时练习)在平面内的直线上求一点,使点到点的距离最小,并求出此最小值.
2.如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,点G与E分别是A1B1和CC1的中点,点D与F分别是AC和AB上的动点.若GD⊥EF,则线段DF长度的最小值为______________.
人教A版高二数学选择性必修第一册1.3 空间向量及其坐标的运算同步精练(解析版)
【题组一 空间向量的坐标运算】
1.(2020·全国高二)已知点,向量,则点坐标是( )
A. B. C. D.
【答案】D
【解析】设点,则向量,
所以,所以点.故选:D
2.(2019·浙江高二学业考试)设点.若,则点B的坐标为( )
A. B. C. D.
【答案】C
【解析】设点B的坐标为,则,
∵,∴,解得,故选:C.
3.(2020·绵竹市南轩中学高二月考(理))若,,,则的值为( )
A. B.5 C.7 D.36
【答案】B
【解析】,.
故选:B
4.(2019·包头市第四中学高二期中(理))若直线的方向向量为,平面的法向量为,则可能使的是( )
A., B.,
C., D.,
【答案】D
【解析】A中,所以排除A;B中,所以排除B;
C中,所以排除C;D中,所以,能使.
故选D
5.(2020·南京市秦淮中学高二期末)对于任意非零向量,,以下说法错误的有( )
A.若,则
B.若,则
C.
D.若,则为单位向量
【答案】BD
【解析】对于A选项,因为,则,A选项正确;
对于B选项,若,且,,若,但分式无意义,B选项错误;
对于C选项,由空间向量数量积的坐标运算可知,C选项正确;
对于D选项,若,则,此时,不是单位向量,D选项错误.
故选:BD.
6(2020·江苏连云港 高二期末)已知点P是△ABC所在的平面外一点,若=(﹣2,1,4),=(1,﹣2,1),=(4,2,0),则( )
A.AP⊥AB B.AP⊥ BP C.BC= D.AP// BC
【答案】AC
【解析】因为,故A正确;,,故B不正确;,,故C正确;,,各个对应分量的比例不同,故D不正确。故选:AC。
7(2020·全国高二课时练习)已知向量.
(1)计算和.
(2)求.
【答案】(1);;(2).
【解析】(1)因为向量
所以,
所以
(2)因为,所以
8.(2020·吴起高级中学高二月考(理))已知空间三点,设.
(1)的夹角的余弦值;
(2)若向量互相垂直,求实数的值;
(3)若向量共线,求实数的值.
【答案】(1);(2)或;(3)或.
【解析】(1)已知空间三点,
(2)若向量互相垂直,
又,则
解得:或
(3)向量共线,又
当时,
当时,,成立,
当时,,不成立,
故:或
【题组二 坐标运算在几何中的运用】
1.(2020·全国高二课时练习)棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别是DD1,BD,BB1的中点.
(1)求证:EF⊥CF;
(2)求与所成角的余弦值;
(3)求CE的长.
【答案】(1)证明见解析;(2);(3).
【解析】建立如图所示的空间直角坐标系Dxyz
则
所以
(1)证明:因为,所以,即EF⊥CF.
(2)因为
.
(3)
2.(2019·全国高二)棱长为1的正方体中,,,分别是,,的中点.
(1)求证:;
(2)求与所成角的余弦值;
(3)求的长.
【答案】(1)详见解析;(2);(3).
【解析】建立如图所示的空间直角坐标系
则,,,,.
所以,
,,.
(1)证明:因为
所以
即
(2)因为
由向量夹角的求法可得
∴
(3)根据空间中两点的距离公式可得
.
3.(2020·全国高二课时练习)在正方体ABCD-A1B1C1D1中,E,F分别为A1D1,BB1的中点,则____,EF=____.
【答案】
【解析】以A为原点,AB,AD,AA1分别为x轴、y轴、z轴建立直角坐标系
设正方体棱长为1,则
.
故答案为:;
4.(2020·全国高二课时练习)如图,在长方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,若以为基底,则向量的坐标为___,向量的坐标为___,向量的坐标为___.
【答案】
【解析】因为,所以向量的坐标为.
因为,
所以向量的坐标为.
因为,所以向量的坐标为.
故答案为:;;
【题组三 最值问题】
1.(2019·全国高一课时练习)在平面内的直线上求一点,使点到点的距离最小,并求出此最小值.
【答案】点的坐标为时,
【解析】设,
则.
所以当,即点的坐标为时,.
2.如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,点G与E分别是A1B1和CC1的中点,点D与F分别是AC和AB上的动点.若GD⊥EF,则线段DF长度的最小值为______________.
【答案】
【解析】建立如图所示的空间直角坐标系,则A(0,0,0),E(0,2,1),G(1,0,2),设F(x,0,0),D(0,y,0),
则,,
由于GD⊥EF,所以,
所以,
故,
所以当时,线段DF长度取得最小值,且最小值为.
故答案为:
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
