人教A版高二数学选择性必修第一册1.4.1 空间向量的应用一同步精练(含解析)
文档属性
| 名称 | 人教A版高二数学选择性必修第一册1.4.1 空间向量的应用一同步精练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 506.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 08:53:40 | ||
图片预览




文档简介
人教A版高二数学选择性必修第一册1.4.1 空间向量的应用一同步精练(原卷版)
【题组一 平面法向量的求解】
1.已知A(1,0,0),B(0,1,0),C(0,0,1),则下列向量是平面ABC法向量的是( )
A.(-1,1,1) B.(1,-1,1)
C. D.
2.(2018·浙江高三其他)平面的法向量,平面的法向量,则下列命题正确的是( )
A.、平行 B.、垂直 C.、重合 D.、不垂直
3.(2019·山东历下.济南一中高二期中)在平面ABCD中,,,,若,且为平面ABCD的法向量,则等于( )
A.2 B.0 C.1 D.无意义
【题组二 空间向量证平行】
1.(2019·安徽埇桥,北大附宿州实验学校高二期末(理))已知平面的法向量是,平面的法向量是,若// ,则的值是( )
A. B.-6 C.6 D.
2(2019·乐清市知临中学高二期末)已知平面α的一个法向量是,,则下列向量可作为平面β的一个法向量的是( )
A. B. C. D.
3.(2020.广东.华侨中学)如图,正方形ABCD与矩形ACEF所在平面互相垂直,AB=,AF=1,M在EF上,且AM∥平面BDE,则M点的坐标为( )
A.(1,1,1)B.C.D.
4.如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M,N分别为A1B和AC上的点,A1M=AN=,则MN与平面BB1C1C的位置关系是( )
A.相交 B.平行
C.垂直 D.MN在平面BB1C1C内
【题组三 空间向量证明垂直】
1.(2019·湖北孝感.高二期中(理))已知向量,平面的一个法向量,若,则( )A., B., C. D.
2.(2020·宜昌市人文艺术高中(宜昌市第二中学)高二月考)已知直线的一个方向向量,平面的一个法向量,若,则______.
3.(2020·陕西富平.期末(理))若直线l的方向向量为,平面的法向量为,则直线l与平面的位置关系是( )
A. B. C. D.l与斜交
4. 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB.
求证:平面BCE⊥平面CDE.
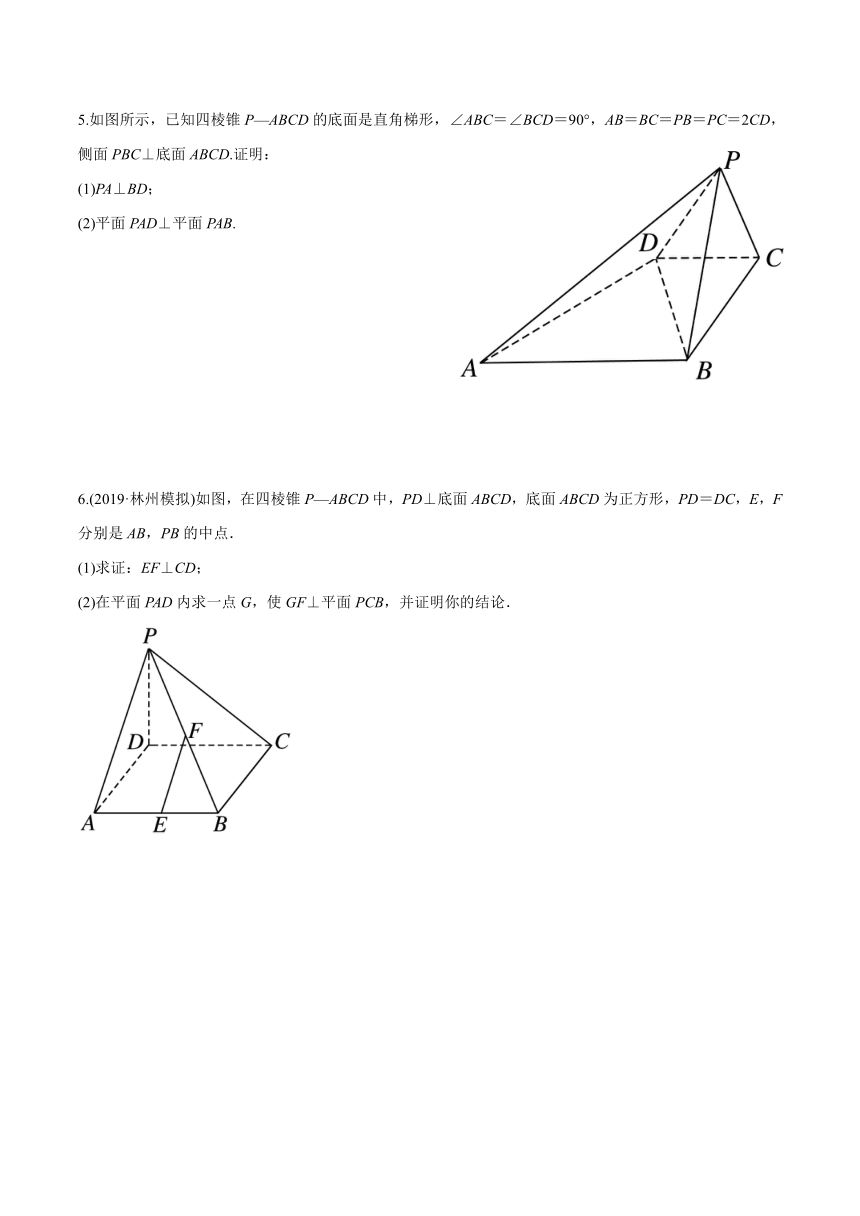
5.如图所示,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD,侧面PBC⊥底面ABCD.证明:
(1)PA⊥BD;
(2)平面PAD⊥平面PAB.
6.(2019·林州模拟)如图,在四棱锥P—ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论.
人教A版高二数学选择性必修第一册1.4.1 空间向量的应用一同步精练(解析版)【题组一 平面法向量的求解】
1.已知A(1,0,0),B(0,1,0),C(0,0,1),则下列向量是平面ABC法向量的是( )
A.(-1,1,1) B.(1,-1,1)
C. D.
【答案】C
【解析】设n=(x,y,z)为平面ABC的法向量,=(-1,1,0),=(-1,0,1),
则化简得∴x=y=z.故选C.
2.(2018·浙江高三其他)平面的法向量,平面的法向量,则下列命题正确的是( )
A.、平行 B.、垂直 C.、重合 D.、不垂直
【答案】B
【解析】平面的法向量,平面的法向量,
因为,所以两个平面垂直.故选:.
3.(2019·山东历下.济南一中高二期中)在平面ABCD中,,,,若,且为平面ABCD的法向量,则等于( )
A.2 B.0 C.1 D.无意义
【答案】C
【解析】由题得,,,又为平面ABCD的法向量,则有,即,则,那么.故选:C
【题组二 空间向量证平行】
1.(2019·安徽埇桥,北大附宿州实验学校高二期末(理))已知平面的法向量是,平面的法向量是,若// ,则的值是( )
A. B.-6 C.6 D.
【答案】C
【解析】因为//,故可得法向量与向量共线,
故可得,解得.故选:C.
2(2019·乐清市知临中学高二期末)已知平面α的一个法向量是,,则下列向量可作为平面β的一个法向量的是( )
A. B. C. D.
【答案】D
【解析】平面α的一个法向量是,,
设平面的法向量为,则,
对比四个选项可知,只有D符合要求,故选:D.
3.(2020.广东.华侨中学)如图,正方形ABCD与矩形ACEF所在平面互相垂直,AB=,AF=1,M在EF上,且AM∥平面BDE,则M点的坐标为( )
A.(1,1,1) B. C. D.
【答案】 C
【解析】设AC与BD相交于O点,连接OE,
∵AM∥平面BDE,且AM 平面ACEF,平面ACEF∩平面BDE=OE,∴AM∥EO,
又O是正方形ABCD对角线的交点,∴M为线段EF的中点.
在空间直角坐标系中,E(0,0,1),F(,,1).
由中点坐标公式,知点M的坐标为.
4.如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M,N分别为A1B和AC上的点,A1M=AN=,则MN与平面BB1C1C的位置关系是( )
A.相交 B.平行
C.垂直 D.MN在平面BB1C1C内
【答案】 B
【解析】以点C1为坐标原点,分别以C1B1,C1D1,C1C所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,由于A1M=AN=,则M,N,=.
又C1D1⊥平面BB1C1C,所以=(0,a,0)为平面BB1C1C的一个法向量.
因为·=0,所以⊥,又MN 平面BB1C1C,所以MN∥平面BB1C1C.
【题组三 空间向量证明垂直】
1.(2019·湖北孝感.高二期中(理))已知向量,平面的一个法向量,若,则( )
A., B., C. D.
【答案】A
【解析】因为,所以,由,得,.故选A
2.(2020·宜昌市人文艺术高中(宜昌市第二中学)高二月考)已知直线的一个方向向量,平面的一个法向量,若,则______.
【答案】
【解析】,,且,,,解得,.
因此,.故答案为:.
3.(2020·陕西富平.期末(理))若直线l的方向向量为,平面的法向量为,则直线l与平面的位置关系是( )
A. B. C. D.l与斜交
【答案】B
【解析】由题得,,则,又是平面的法向量,是直线l的方向向量,可得.
故选:B
4. 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB.
求证:平面BCE⊥平面CDE.
【答案】
【解析】设AD=DE=2AB=2a,
以A为原点,分别以AC,AB所在直线为x轴,z轴,以过点A垂直于AC的直线为y轴,建立如图所示的空间直角坐标系Axyz,则A(0,0,0),C(2a,0,0),B(0,0,a),D(a,a,0),
E(a,a,2a).
所以=(a,a,a),=(2a,0,-a),=(-a,a,0),=(0,0,-2a).
设平面BCE的法向量为n1=(x1,y1,z1),由n1·=0,n1·=0可得
即令z1=2,可得n1=(1,-,2).
设平面CDE的法向量为n2=(x2,y2,z2),由n2·=0,n2·=0可得
即
令y2=1,可得n2=(,1,0).因为n1·n2=1×+1×(-)+2×0=0.所以n1⊥n2,
所以平面BCE⊥平面CDE.
5.如图所示,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD,侧面PBC⊥底面ABCD.证明:
(1)PA⊥BD;
(2)平面PAD⊥平面PAB.
【答案】见解析
【解析】 (1)取BC的中点O,连接PO,
∵平面PBC⊥底面ABCD,△PBC为等边三角形,平面PBC∩底面ABCD=BC,PO 平面PBC,
∴PO⊥底面ABCD.
以BC的中点O为坐标原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,OP所在直线为z轴,建立空间直角坐标系,如图所示.
不妨设CD=1,则AB=BC=2,PO=,
∴A(1,-2,0),B(1,0,0),D(-1,-1,0),P(0,0,),
∴=(-2,-1,0),=(1,-2,-).
∵·=(-2)×1+(-1)×(-2)+0×(-)=0,
∴⊥,
∴PA⊥BD.
(2)取PA的中点M,连接DM,则M.
∵=,=(1,0,-),
∴·=×1+0×0+×(-)=0,
∴⊥,即DM⊥PB.
∵·=×1+0×(-2)+×(-)=0,
∴⊥,即DM⊥PA.
又∵PA∩PB=P,PA,PB 平面PAB,
∴DM⊥平面PAB.
∵DM 平面PAD,∴平面PAD⊥平面PAB.
6.(2019·林州模拟)如图,在四棱锥P—ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论.
【答案】见解析
【解析】(1)证明 如图,以D为原点,分别以DA,DC,DP所在直线为x轴、y轴、z轴建立空间直角坐标系,
设AD=a,则D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),E,P(0,0,a),F.
=,=(0,a,0).
∵·=0,∴⊥,即EF⊥CD.
(2)解 设G(x,0,z),则=,
若使GF⊥平面PCB,则需·=0,且·=0,
由·=·(a,0,0)
=a=0,得x=;
由·=·(0,-a,a)
=+a=0,得z=0.
∴G点坐标为,即G为AD的中点.
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
【题组一 平面法向量的求解】
1.已知A(1,0,0),B(0,1,0),C(0,0,1),则下列向量是平面ABC法向量的是( )
A.(-1,1,1) B.(1,-1,1)
C. D.
2.(2018·浙江高三其他)平面的法向量,平面的法向量,则下列命题正确的是( )
A.、平行 B.、垂直 C.、重合 D.、不垂直
3.(2019·山东历下.济南一中高二期中)在平面ABCD中,,,,若,且为平面ABCD的法向量,则等于( )
A.2 B.0 C.1 D.无意义
【题组二 空间向量证平行】
1.(2019·安徽埇桥,北大附宿州实验学校高二期末(理))已知平面的法向量是,平面的法向量是,若// ,则的值是( )
A. B.-6 C.6 D.
2(2019·乐清市知临中学高二期末)已知平面α的一个法向量是,,则下列向量可作为平面β的一个法向量的是( )
A. B. C. D.
3.(2020.广东.华侨中学)如图,正方形ABCD与矩形ACEF所在平面互相垂直,AB=,AF=1,M在EF上,且AM∥平面BDE,则M点的坐标为( )
A.(1,1,1)B.C.D.
4.如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M,N分别为A1B和AC上的点,A1M=AN=,则MN与平面BB1C1C的位置关系是( )
A.相交 B.平行
C.垂直 D.MN在平面BB1C1C内
【题组三 空间向量证明垂直】
1.(2019·湖北孝感.高二期中(理))已知向量,平面的一个法向量,若,则( )A., B., C. D.
2.(2020·宜昌市人文艺术高中(宜昌市第二中学)高二月考)已知直线的一个方向向量,平面的一个法向量,若,则______.
3.(2020·陕西富平.期末(理))若直线l的方向向量为,平面的法向量为,则直线l与平面的位置关系是( )
A. B. C. D.l与斜交
4. 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB.
求证:平面BCE⊥平面CDE.
5.如图所示,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD,侧面PBC⊥底面ABCD.证明:
(1)PA⊥BD;
(2)平面PAD⊥平面PAB.
6.(2019·林州模拟)如图,在四棱锥P—ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论.
人教A版高二数学选择性必修第一册1.4.1 空间向量的应用一同步精练(解析版)【题组一 平面法向量的求解】
1.已知A(1,0,0),B(0,1,0),C(0,0,1),则下列向量是平面ABC法向量的是( )
A.(-1,1,1) B.(1,-1,1)
C. D.
【答案】C
【解析】设n=(x,y,z)为平面ABC的法向量,=(-1,1,0),=(-1,0,1),
则化简得∴x=y=z.故选C.
2.(2018·浙江高三其他)平面的法向量,平面的法向量,则下列命题正确的是( )
A.、平行 B.、垂直 C.、重合 D.、不垂直
【答案】B
【解析】平面的法向量,平面的法向量,
因为,所以两个平面垂直.故选:.
3.(2019·山东历下.济南一中高二期中)在平面ABCD中,,,,若,且为平面ABCD的法向量,则等于( )
A.2 B.0 C.1 D.无意义
【答案】C
【解析】由题得,,,又为平面ABCD的法向量,则有,即,则,那么.故选:C
【题组二 空间向量证平行】
1.(2019·安徽埇桥,北大附宿州实验学校高二期末(理))已知平面的法向量是,平面的法向量是,若// ,则的值是( )
A. B.-6 C.6 D.
【答案】C
【解析】因为//,故可得法向量与向量共线,
故可得,解得.故选:C.
2(2019·乐清市知临中学高二期末)已知平面α的一个法向量是,,则下列向量可作为平面β的一个法向量的是( )
A. B. C. D.
【答案】D
【解析】平面α的一个法向量是,,
设平面的法向量为,则,
对比四个选项可知,只有D符合要求,故选:D.
3.(2020.广东.华侨中学)如图,正方形ABCD与矩形ACEF所在平面互相垂直,AB=,AF=1,M在EF上,且AM∥平面BDE,则M点的坐标为( )
A.(1,1,1) B. C. D.
【答案】 C
【解析】设AC与BD相交于O点,连接OE,
∵AM∥平面BDE,且AM 平面ACEF,平面ACEF∩平面BDE=OE,∴AM∥EO,
又O是正方形ABCD对角线的交点,∴M为线段EF的中点.
在空间直角坐标系中,E(0,0,1),F(,,1).
由中点坐标公式,知点M的坐标为.
4.如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M,N分别为A1B和AC上的点,A1M=AN=,则MN与平面BB1C1C的位置关系是( )
A.相交 B.平行
C.垂直 D.MN在平面BB1C1C内
【答案】 B
【解析】以点C1为坐标原点,分别以C1B1,C1D1,C1C所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,由于A1M=AN=,则M,N,=.
又C1D1⊥平面BB1C1C,所以=(0,a,0)为平面BB1C1C的一个法向量.
因为·=0,所以⊥,又MN 平面BB1C1C,所以MN∥平面BB1C1C.
【题组三 空间向量证明垂直】
1.(2019·湖北孝感.高二期中(理))已知向量,平面的一个法向量,若,则( )
A., B., C. D.
【答案】A
【解析】因为,所以,由,得,.故选A
2.(2020·宜昌市人文艺术高中(宜昌市第二中学)高二月考)已知直线的一个方向向量,平面的一个法向量,若,则______.
【答案】
【解析】,,且,,,解得,.
因此,.故答案为:.
3.(2020·陕西富平.期末(理))若直线l的方向向量为,平面的法向量为,则直线l与平面的位置关系是( )
A. B. C. D.l与斜交
【答案】B
【解析】由题得,,则,又是平面的法向量,是直线l的方向向量,可得.
故选:B
4. 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB.
求证:平面BCE⊥平面CDE.
【答案】
【解析】设AD=DE=2AB=2a,
以A为原点,分别以AC,AB所在直线为x轴,z轴,以过点A垂直于AC的直线为y轴,建立如图所示的空间直角坐标系Axyz,则A(0,0,0),C(2a,0,0),B(0,0,a),D(a,a,0),
E(a,a,2a).
所以=(a,a,a),=(2a,0,-a),=(-a,a,0),=(0,0,-2a).
设平面BCE的法向量为n1=(x1,y1,z1),由n1·=0,n1·=0可得
即令z1=2,可得n1=(1,-,2).
设平面CDE的法向量为n2=(x2,y2,z2),由n2·=0,n2·=0可得
即
令y2=1,可得n2=(,1,0).因为n1·n2=1×+1×(-)+2×0=0.所以n1⊥n2,
所以平面BCE⊥平面CDE.
5.如图所示,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD,侧面PBC⊥底面ABCD.证明:
(1)PA⊥BD;
(2)平面PAD⊥平面PAB.
【答案】见解析
【解析】 (1)取BC的中点O,连接PO,
∵平面PBC⊥底面ABCD,△PBC为等边三角形,平面PBC∩底面ABCD=BC,PO 平面PBC,
∴PO⊥底面ABCD.
以BC的中点O为坐标原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,OP所在直线为z轴,建立空间直角坐标系,如图所示.
不妨设CD=1,则AB=BC=2,PO=,
∴A(1,-2,0),B(1,0,0),D(-1,-1,0),P(0,0,),
∴=(-2,-1,0),=(1,-2,-).
∵·=(-2)×1+(-1)×(-2)+0×(-)=0,
∴⊥,
∴PA⊥BD.
(2)取PA的中点M,连接DM,则M.
∵=,=(1,0,-),
∴·=×1+0×0+×(-)=0,
∴⊥,即DM⊥PB.
∵·=×1+0×(-2)+×(-)=0,
∴⊥,即DM⊥PA.
又∵PA∩PB=P,PA,PB 平面PAB,
∴DM⊥平面PAB.
∵DM 平面PAD,∴平面PAD⊥平面PAB.
6.(2019·林州模拟)如图,在四棱锥P—ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论.
【答案】见解析
【解析】(1)证明 如图,以D为原点,分别以DA,DC,DP所在直线为x轴、y轴、z轴建立空间直角坐标系,
设AD=a,则D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),E,P(0,0,a),F.
=,=(0,a,0).
∵·=0,∴⊥,即EF⊥CD.
(2)解 设G(x,0,z),则=,
若使GF⊥平面PCB,则需·=0,且·=0,
由·=·(a,0,0)
=a=0,得x=;
由·=·(0,-a,a)
=+a=0,得z=0.
∴G点坐标为,即G为AD的中点.
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
