多边形的内角和[下学期]
文档属性
| 名称 | 多边形的内角和[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 666.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-10 19:52:00 | ||
图片预览







文档简介
课件29张PPT。§7.3.2多边形的内角和小明想:2008年奥运会在北京举行,设计一个内角和为20080的多边形图案该多好,你说小明的想法能实现吗?为什么?问题1:提出问题问题1:
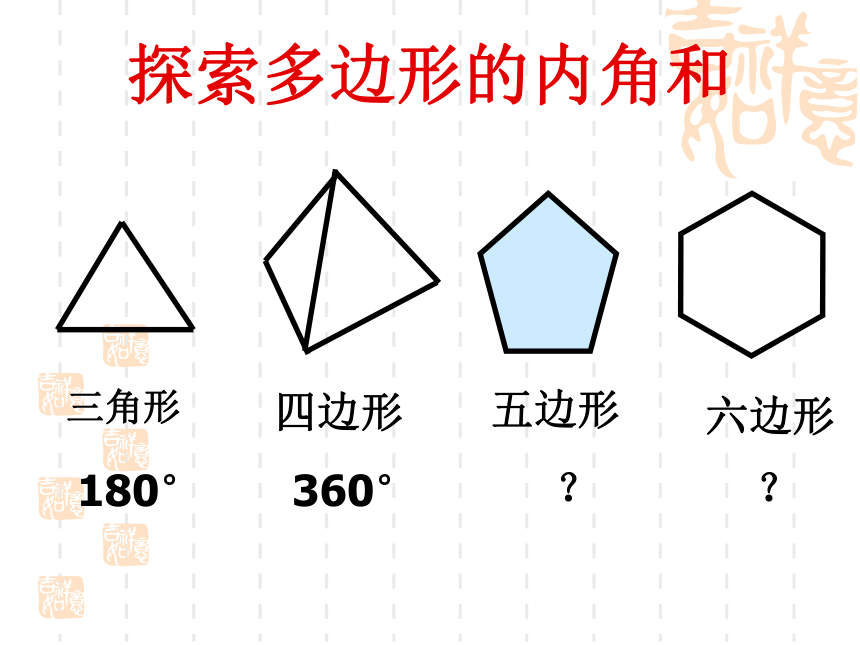
我们已学过哪些多边形的内角和?问题2:
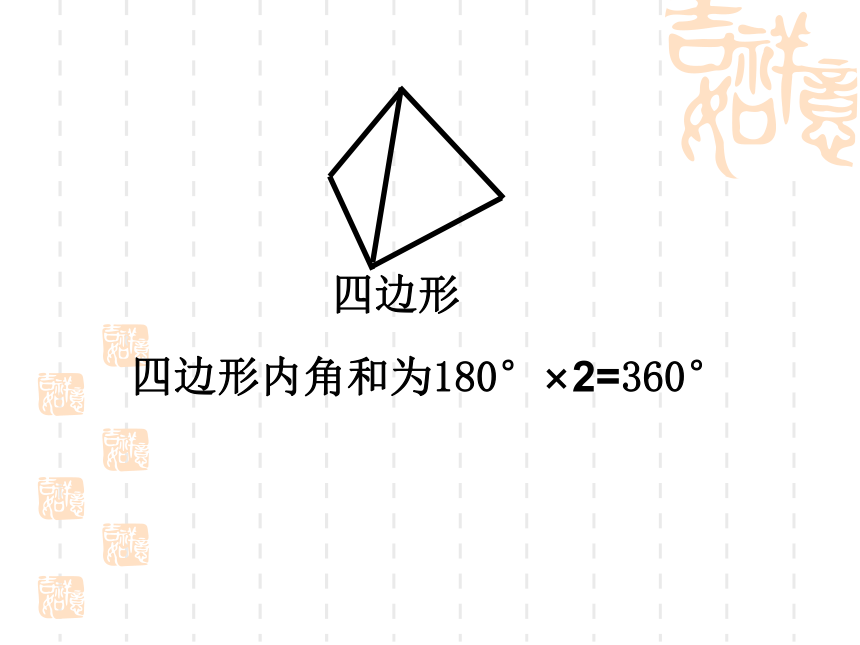
任意四边形的内角和是多少?试一试画一画:任意画一个四边形。
量一量:量出四边形的四个内角。算一算: 计算四个内角的和.能否利用三角形内角和等于180°得出这个结论?四边形内角和为180°×2=360°三角形 六边形 四边形探索多边形的内角和五边形180°360°??做一做你能仿照四边形求内角和的方法,求出五边形、六边形的的内角和吗? 那n边形呢? nn-23×18004×1800(n-2)×18002344562×18001230nn-13454563×180°-180°4×180°- 180°5×180° -180°(n-1)180° -180°1230nn4564564×180°-360°5×180°- 360°6×180° -360°n×180° -360°1230n边形内角和为(n-2)×1800五边形180°360°540°n边形1.快速抢答 (1)8边形内角和是_______。 (2)32边形内角和是________。 (3)如果一个四边形的一组对角互补,那 么另一组对角的关系是______。 (4)一个多边形的内角和是1440°,它是_____边形。练一练5400°1080°互补十 1、下面是小明准备用来做徽章的木板,
求下列木板图中x的值.走进生活:小明想:2008年奥运会在北京举行,设计一个内角和为20080的多边形图案该多好,你说小明的想法能实现吗?为什么?问题1:C3.某同学计算了几个多边形的内角和,经检查他很快就发现错了一个,你能发现他的错误吗?-----------------( )
A、9000 ° ; B、 5400 °; C、19000 °; D、1801800 °。 清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出?1+ ? 2+ ? 3+ ? 4+ ? 5=吗?你是怎样得到的?探究 清晨,小明沿一个五边形广场周围的小路跑步,按逆时针方向跑步。 请你观察并思考如下几个问题(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们(2)他每跑完一圈,身体转过的角度之和是多少?(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的? 演示实验的方法360°在一张纸上画一个类似的五边形
广场,将∠1、∠2、∠3、∠4、
∠5剪来,顶点拼在一起恰好组成一个周角,因此
∠1+∠2+∠3+∠4+∠5= 解:∵∠1+∠6=180°,
∠2+∠7=180°,
∠3+∠8=180°,
∠4+∠9=180°,
∠5+∠10=180° 推理证明法:∴∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9+∠10 =180×5=900°∴ ∠1+∠2+∠3+∠4+∠5 =360° ∵∠6+∠7+∠8+∠9+∠10 =(5-2)×180°=540° 每个内角都是108°的多边形是几边形?解:设多边形的边数为n,
根据题意得(n-2)×180=108n 180n-360=108n 答:这多边形是五边形。72n=360n=5用一用每个内角都是108°的多边形是几边形?解: 由题意得,这个多边形的每个外角 都是72o ,答:这多边形是五边形。则它的边数为360÷ 72 =5用一用[例]一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是
(n-2)·180°,外角和等于360°,
∴ (n-2)·180=3×360
解得:n=8
答:这个多边形是八边形. 例题赏析挑战自我2.一个多边形的各内角都等于120°,它是几边形?1.一个多边形的各外角都等于60°,它是几边形?3.一个多边形的每一个内角都相等,且它的一个外角与一个内角的比是1:3,求这个多边形的内角和.课时小结通过本节课的学习,你学到了哪些知识?有何体会?谢谢!
我们已学过哪些多边形的内角和?问题2:
任意四边形的内角和是多少?试一试画一画:任意画一个四边形。
量一量:量出四边形的四个内角。算一算: 计算四个内角的和.能否利用三角形内角和等于180°得出这个结论?四边形内角和为180°×2=360°三角形 六边形 四边形探索多边形的内角和五边形180°360°??做一做你能仿照四边形求内角和的方法,求出五边形、六边形的的内角和吗? 那n边形呢? nn-23×18004×1800(n-2)×18002344562×18001230nn-13454563×180°-180°4×180°- 180°5×180° -180°(n-1)180° -180°1230nn4564564×180°-360°5×180°- 360°6×180° -360°n×180° -360°1230n边形内角和为(n-2)×1800五边形180°360°540°n边形1.快速抢答 (1)8边形内角和是_______。 (2)32边形内角和是________。 (3)如果一个四边形的一组对角互补,那 么另一组对角的关系是______。 (4)一个多边形的内角和是1440°,它是_____边形。练一练5400°1080°互补十 1、下面是小明准备用来做徽章的木板,
求下列木板图中x的值.走进生活:小明想:2008年奥运会在北京举行,设计一个内角和为20080的多边形图案该多好,你说小明的想法能实现吗?为什么?问题1:C3.某同学计算了几个多边形的内角和,经检查他很快就发现错了一个,你能发现他的错误吗?-----------------( )
A、9000 ° ; B、 5400 °; C、19000 °; D、1801800 °。 清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出?1+ ? 2+ ? 3+ ? 4+ ? 5=吗?你是怎样得到的?探究 清晨,小明沿一个五边形广场周围的小路跑步,按逆时针方向跑步。 请你观察并思考如下几个问题(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们(2)他每跑完一圈,身体转过的角度之和是多少?(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的? 演示实验的方法360°在一张纸上画一个类似的五边形
广场,将∠1、∠2、∠3、∠4、
∠5剪来,顶点拼在一起恰好组成一个周角,因此
∠1+∠2+∠3+∠4+∠5= 解:∵∠1+∠6=180°,
∠2+∠7=180°,
∠3+∠8=180°,
∠4+∠9=180°,
∠5+∠10=180° 推理证明法:∴∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9+∠10 =180×5=900°∴ ∠1+∠2+∠3+∠4+∠5 =360° ∵∠6+∠7+∠8+∠9+∠10 =(5-2)×180°=540° 每个内角都是108°的多边形是几边形?解:设多边形的边数为n,
根据题意得(n-2)×180=108n 180n-360=108n 答:这多边形是五边形。72n=360n=5用一用每个内角都是108°的多边形是几边形?解: 由题意得,这个多边形的每个外角 都是72o ,答:这多边形是五边形。则它的边数为360÷ 72 =5用一用[例]一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是
(n-2)·180°,外角和等于360°,
∴ (n-2)·180=3×360
解得:n=8
答:这个多边形是八边形. 例题赏析挑战自我2.一个多边形的各内角都等于120°,它是几边形?1.一个多边形的各外角都等于60°,它是几边形?3.一个多边形的每一个内角都相等,且它的一个外角与一个内角的比是1:3,求这个多边形的内角和.课时小结通过本节课的学习,你学到了哪些知识?有何体会?谢谢!
