2023-2024学年人教版七年级数学上册4.1.2点、线、面、体课件 23张PPT
文档属性
| 名称 | 2023-2024学年人教版七年级数学上册4.1.2点、线、面、体课件 23张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 523.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-28 13:09:09 | ||
图片预览








文档简介
(共23张PPT)
第四章 几何图形初步
点、线、面、体
教学目标
【知识与技能】
(1)了解几何体、平面和曲面的意义,能正确判断围成几何体的面是平面还是曲面.
(2)了解构成几何图形的基本元素是点、线、面,理解点、线、面经过运动变化形成的几何图形.
【过程与方法】
经历探索点、线、面、体的关系的数学活动,提高空间想象能力和抽象思维能力.
【情感态度与价值观】
经历本节课的数学活动,使学生养成主动探索、求知的学习态度,激发学生对数学的学习兴趣,并让学生体验数学活动中小组合作的重要性.
教学重难点
1正确判断围成的立体图形的面是平面还是曲面,探索点、线、面、体之间的关系.
2理解点、线、面经过运动变化后形成的图形.
1.(2022新课标)通过实物和模型,了解从物体抽象出来的几何体、平面、直线和点等概念.
2.进一步认识点、线、面、体的几何特征,感受它们之间的关系.
知识点一:点、线、面、体的概念及构成图形的元素
(1)几何体也简称 ,包围着体的是 ,面有平面和 两种.
(2)面和面相交的地方是 ,线有直线和 两种.
(3)线和线相交的地方是 .
(4)几何图形都是由 、 、 、 组成的, 是构成图形的基本元素.
点
体
面
线
点
点
曲线
线
曲面
面
体
1.(1)在球、圆锥、圆柱、棱柱中,由曲面和平面组成的是( )
A.球和圆锥 B.球和圆柱
C.圆锥和圆柱 D.圆柱和棱柱
C
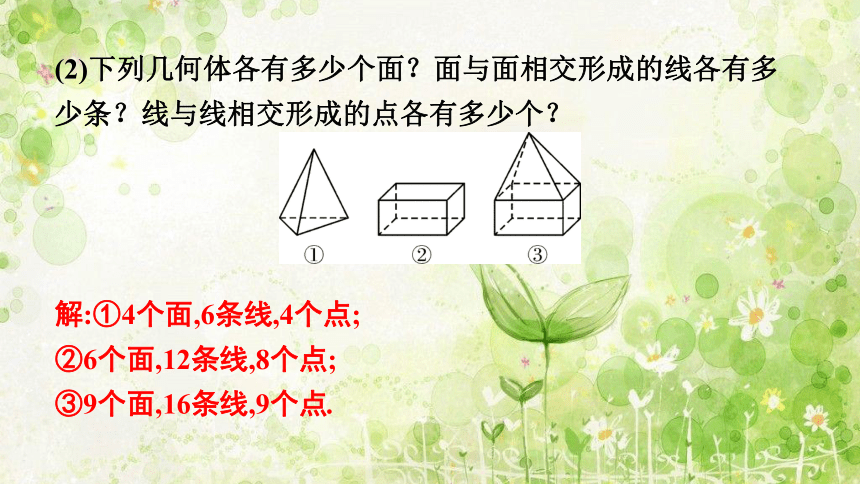
(2)下列几何体各有多少个面?面与面相交形成的线各有多少条?线与线相交形成的点各有多少个?
解:①4个面,6条线,4个点;
②6个面,12条线,8个点;
③9个面,16条线,9个点.
知识点二:点、线、面、体的关系及几何图形的组成
(1)笔尖可以看作一个点,这个点在纸上运动时,就形成
,节日的焰火也可以看成由点运动形成的,这可以
说 .汽车的雨刷在挡风玻璃上画出一个扇面,这可以说 .长方形硬纸片绕它的一边旋转,
形成一个圆柱体,这可以说 .
(2)—般地,有曲面的几何体都可以由某个平面图形旋转得到.将一个平面图形旋转成立体图形需要明确旋转轴和
两个条件.
旋转角
面动成体
线动成面
点动成线
线
(3)一个平面图形旋转后得到一个立体图形,这个立体图形的形状取决于两个因素:
①平面图形的 ;
②旋转时所绕的轴的 .
(4)点、线、面、体经过运动变化,就能组合成各种各样的几何图形,形成多姿多彩的图形世界.
位置
形状
2.(1)(跨学科融合)神舟十三号载人飞船返回舱拖着“长长的火焰”,我们用数学知识可解释为点动成线.请解释下列现象:
①一只小蚂蚁爬行留下的路线,可解释为 ;
②电动车的车辐条运动形成的图形,可解释为 ;
③薄薄的硬币在桌面上转动时,看上去像球体,可解释为
.
面动成体
线动成面
点动成线
(2)(人教7上P120、北师7上P7)如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,把有对应关系的平面图形与立体图形连接起来.
3.【例1】(人教7上P119、北师7上P7)观察图形,回答下列问题:
(1)图①由几个面组成?这些面有什么特征?
(2)图②由几个面组成?这些面有什么特征?
(3)图①中共形成了多少条线?这些线都是直的吗?图②呢?
(4)图①和图②中各有几个顶点?
解:(1)图①由6个面组成,这些面都是平面.
(2)图②由2个面组成,1个平面和1个曲面.
(3)图①中共有12条线,这些线都是直的;图②中有1条线,是曲线.
(4)图①中有8个顶点,图②中只有1个顶点.
小结:解答此类问题要联系实物的形状与面的形状作对比,然后作出判断,平面与平面相交成直线,曲面与平面相交成曲线.
小结:此题考查了点、线、面、体,重在体现面动成体,需要发挥立体图形的空间想象能力及提高分析问题、解决问题的能力.
A B C D
4.【例2】把如图所示的图形绕着给定的直线旋转一周后形成的几何体是( )
D
5.【例3】将一个长4 cm、宽2 cm的长方形绕它的一边所在的直线旋转一周,所得几何体的底面周长是多少?(结果保留π)
解:分两种情况:
①绕宽所在的直线旋转一周得到圆柱的底面周长是2π×4=8π(cm);
②绕长所在的直线旋转一周得到圆柱的底面周长是2π×2=4π(cm).
故所得几何体的底面周长是8π cm或4π cm.
小结:先判断旋转后的立体图形的形状,再确定底面的平面图形的形状是圆,得到圆的半径,最后利用圆的周长计算公式解答.
名称 三棱柱 四棱柱 五棱柱 六棱柱
图形
顶点数 6 10 12
棱数 9 12
面数 5 8
7
6.观察下列立体图形,并把下表补充完整.
6
8
18
15
7.(1)(跨学科融合)在朱自清的《春》中有描写春雨“像牛毛、像花针、像细丝,密密麻麻地斜织着”的语句,这里把雨看成了线,这说明了( )
A.点动成线 B.线动成面
C.面动成体 D.以上都不对
A
A B C D
(2)(人教7上P122、北师7上P6)将下列平面图形绕轴旋转一周,可得到图中所示的立体图形的是( )
A
★8.直角三角形的两直角边长分别为8 cm,6 cm,以其中一条直角边所在直线为轴旋转一周,得到的几何体的底面积是多少?(结果保留π)
解:分两种情况:
①以较短直角边所在的直线为轴旋转一周得到的圆锥的底面积是π×82=64π(cm2);
②以较长直角边所在的直线为轴旋转一周得到的圆锥的底面积是π×62=36π(cm2).
故得到的几何体的底面积是64π cm2或36π cm2.
小结:本节课通过丰富的实例,认识点、线、面、体,并感受它们之间的关系:点动成线,线动成面,面动成体.
教材P122习题4.1第5题
谢 谢
第四章 几何图形初步
点、线、面、体
教学目标
【知识与技能】
(1)了解几何体、平面和曲面的意义,能正确判断围成几何体的面是平面还是曲面.
(2)了解构成几何图形的基本元素是点、线、面,理解点、线、面经过运动变化形成的几何图形.
【过程与方法】
经历探索点、线、面、体的关系的数学活动,提高空间想象能力和抽象思维能力.
【情感态度与价值观】
经历本节课的数学活动,使学生养成主动探索、求知的学习态度,激发学生对数学的学习兴趣,并让学生体验数学活动中小组合作的重要性.
教学重难点
1正确判断围成的立体图形的面是平面还是曲面,探索点、线、面、体之间的关系.
2理解点、线、面经过运动变化后形成的图形.
1.(2022新课标)通过实物和模型,了解从物体抽象出来的几何体、平面、直线和点等概念.
2.进一步认识点、线、面、体的几何特征,感受它们之间的关系.
知识点一:点、线、面、体的概念及构成图形的元素
(1)几何体也简称 ,包围着体的是 ,面有平面和 两种.
(2)面和面相交的地方是 ,线有直线和 两种.
(3)线和线相交的地方是 .
(4)几何图形都是由 、 、 、 组成的, 是构成图形的基本元素.
点
体
面
线
点
点
曲线
线
曲面
面
体
1.(1)在球、圆锥、圆柱、棱柱中,由曲面和平面组成的是( )
A.球和圆锥 B.球和圆柱
C.圆锥和圆柱 D.圆柱和棱柱
C
(2)下列几何体各有多少个面?面与面相交形成的线各有多少条?线与线相交形成的点各有多少个?
解:①4个面,6条线,4个点;
②6个面,12条线,8个点;
③9个面,16条线,9个点.
知识点二:点、线、面、体的关系及几何图形的组成
(1)笔尖可以看作一个点,这个点在纸上运动时,就形成
,节日的焰火也可以看成由点运动形成的,这可以
说 .汽车的雨刷在挡风玻璃上画出一个扇面,这可以说 .长方形硬纸片绕它的一边旋转,
形成一个圆柱体,这可以说 .
(2)—般地,有曲面的几何体都可以由某个平面图形旋转得到.将一个平面图形旋转成立体图形需要明确旋转轴和
两个条件.
旋转角
面动成体
线动成面
点动成线
线
(3)一个平面图形旋转后得到一个立体图形,这个立体图形的形状取决于两个因素:
①平面图形的 ;
②旋转时所绕的轴的 .
(4)点、线、面、体经过运动变化,就能组合成各种各样的几何图形,形成多姿多彩的图形世界.
位置
形状
2.(1)(跨学科融合)神舟十三号载人飞船返回舱拖着“长长的火焰”,我们用数学知识可解释为点动成线.请解释下列现象:
①一只小蚂蚁爬行留下的路线,可解释为 ;
②电动车的车辐条运动形成的图形,可解释为 ;
③薄薄的硬币在桌面上转动时,看上去像球体,可解释为
.
面动成体
线动成面
点动成线
(2)(人教7上P120、北师7上P7)如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,把有对应关系的平面图形与立体图形连接起来.
3.【例1】(人教7上P119、北师7上P7)观察图形,回答下列问题:
(1)图①由几个面组成?这些面有什么特征?
(2)图②由几个面组成?这些面有什么特征?
(3)图①中共形成了多少条线?这些线都是直的吗?图②呢?
(4)图①和图②中各有几个顶点?
解:(1)图①由6个面组成,这些面都是平面.
(2)图②由2个面组成,1个平面和1个曲面.
(3)图①中共有12条线,这些线都是直的;图②中有1条线,是曲线.
(4)图①中有8个顶点,图②中只有1个顶点.
小结:解答此类问题要联系实物的形状与面的形状作对比,然后作出判断,平面与平面相交成直线,曲面与平面相交成曲线.
小结:此题考查了点、线、面、体,重在体现面动成体,需要发挥立体图形的空间想象能力及提高分析问题、解决问题的能力.
A B C D
4.【例2】把如图所示的图形绕着给定的直线旋转一周后形成的几何体是( )
D
5.【例3】将一个长4 cm、宽2 cm的长方形绕它的一边所在的直线旋转一周,所得几何体的底面周长是多少?(结果保留π)
解:分两种情况:
①绕宽所在的直线旋转一周得到圆柱的底面周长是2π×4=8π(cm);
②绕长所在的直线旋转一周得到圆柱的底面周长是2π×2=4π(cm).
故所得几何体的底面周长是8π cm或4π cm.
小结:先判断旋转后的立体图形的形状,再确定底面的平面图形的形状是圆,得到圆的半径,最后利用圆的周长计算公式解答.
名称 三棱柱 四棱柱 五棱柱 六棱柱
图形
顶点数 6 10 12
棱数 9 12
面数 5 8
7
6.观察下列立体图形,并把下表补充完整.
6
8
18
15
7.(1)(跨学科融合)在朱自清的《春》中有描写春雨“像牛毛、像花针、像细丝,密密麻麻地斜织着”的语句,这里把雨看成了线,这说明了( )
A.点动成线 B.线动成面
C.面动成体 D.以上都不对
A
A B C D
(2)(人教7上P122、北师7上P6)将下列平面图形绕轴旋转一周,可得到图中所示的立体图形的是( )
A
★8.直角三角形的两直角边长分别为8 cm,6 cm,以其中一条直角边所在直线为轴旋转一周,得到的几何体的底面积是多少?(结果保留π)
解:分两种情况:
①以较短直角边所在的直线为轴旋转一周得到的圆锥的底面积是π×82=64π(cm2);
②以较长直角边所在的直线为轴旋转一周得到的圆锥的底面积是π×62=36π(cm2).
故得到的几何体的底面积是64π cm2或36π cm2.
小结:本节课通过丰富的实例,认识点、线、面、体,并感受它们之间的关系:点动成线,线动成面,面动成体.
教材P122习题4.1第5题
谢 谢
