2023-2024学年人教版七年级数学上册4.1.1立体图形与平面图形(2)课件 29张PPT
文档属性
| 名称 | 2023-2024学年人教版七年级数学上册4.1.1立体图形与平面图形(2)课件 29张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 712.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-28 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
第四章 几何图形初步
立体图形与平面图形(2)
教学目标
【知识与技能】
(1)能从实物中抽象出几何图形,正确区分立体图形与平面图形;
(2)能把一些立体图形的问题转化为平面图形的问题进行研究和解决,探究平面图形与立体图形之间的关系
【过程与方法】
经历探究平面图形与立体图形之间的关系,发展空间观念,培养观察、分析、抽象、概括的能力以及动手操作的能力.
【情感态度与价值观】
通过本节课的数学活动,使学生养成主动探索、求知的学习态度,激发学生对数学知识的求知欲,并让学生体会数学活动中小组合作的重要性.
教学重难点
1熟悉常见的立体图形的表面展开图,并能根据立体图形的表面展开图还原立体图形;从不同方向观察立体图形得到的平面图形.
2由立体图形的表面展开图还原立体图形.
1.经历从不同方向观察物体的活动过程,初步体会从不同方向观察同一物体可能看到不一样的结果.
2.能画一些简单几何体以及由它们组成的简单组合体展开得到的平面图形.
3.(2022新课标)了解直棱柱、圆锥的侧面展开图,能根据展开图想象和制作模型.
知识点一:从不同方向看简单立体图形
(1)对于一些立体图形的问题,常把它们转化为平面图形来研究和处理.从不同方向看立体图形,往往会得到不同形状的平面图形.
(2)通常我们是从正面、 、 三个方向看,从而得到相应的平面图形.
上面
左面
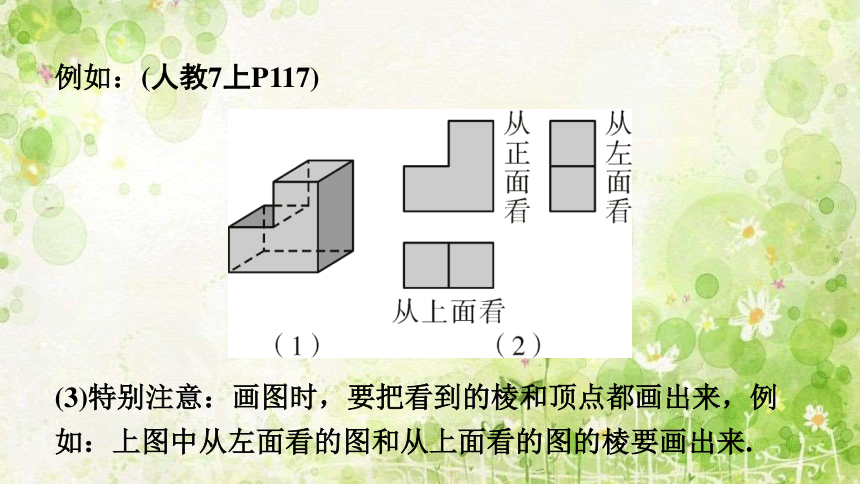
例如:(人教7上P117)
(3)特别注意:画图时,要把看到的棱和顶点都画出来,例如:上图中从左面看的图和从上面看的图的棱要画出来.
1.(1)(人教7上P121、北师9上P135)如图,分别从正面、左面、上面观察这些立体图形,各能得到什么平面图形?
解:圆柱:长方形、长方形、圆;
圆锥:三角形、三角形、圆(带圆心);
球:圆、圆、圆.
A B C D
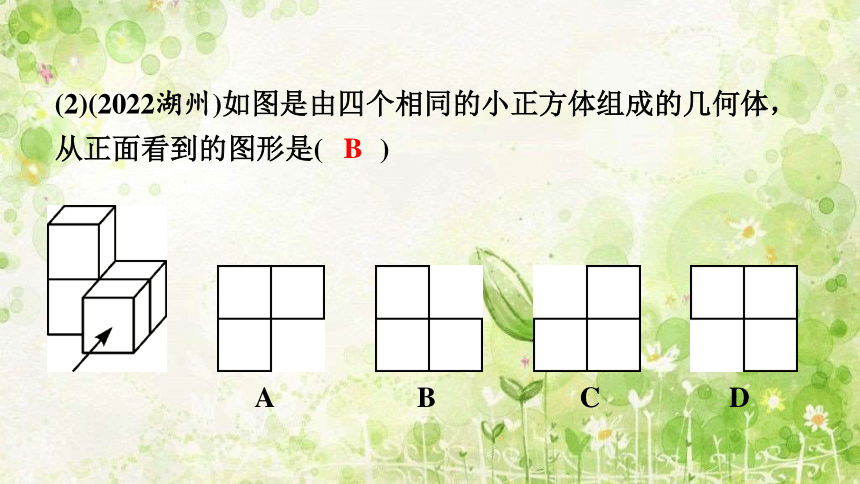
(2)(2022湖州)如图是由四个相同的小正方体组成的几何体,从正面看到的图形是( )
B
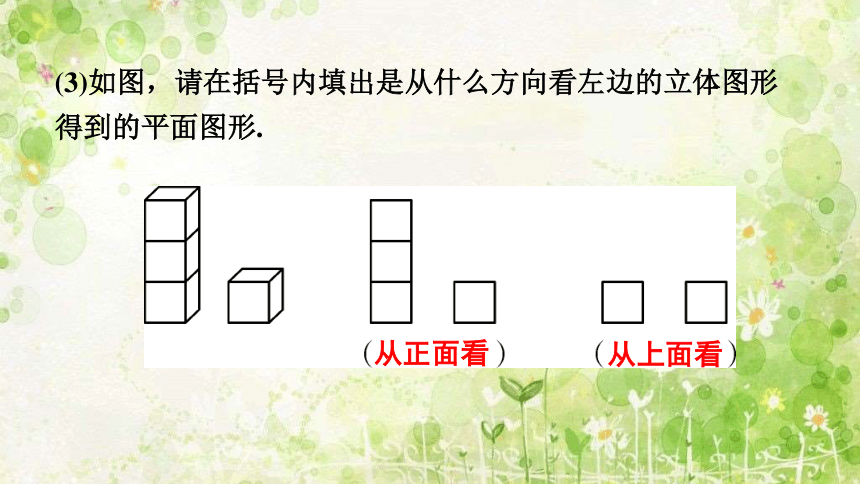
(3)如图,请在括号内填出是从什么方向看左边的立体图形得到的平面图形.
从正面看
从上面看
知识点二:立体图形的展开图
(1)有些 是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形.这样的平面图形称为相应立体图形的 .
(2)不是所有的 都可以展开成平面图形,例如:球体便不可以展开.
(3)同一立体图形按不同的方式展开,可以得到不同的平面
.
展开图
立体图形
展开图
立体图形
2.(1)(2022广元)如图是某几何体的展开图,该几何体是( )
A.长方体 B.圆柱
C.圆锥 D.三棱柱
B
A B C D
(2)(人教7上P119、北师7上P8-9)下列图形中,不是正方体的表面展开图的是( )
D
知识点三:平面图形的折叠
(1)同一立体图形沿不同方式展开,得到的平面展开图可能
;不同形状的平面图形经过折叠可能得到相同的立体图形.
(2)对于立体图形问题,我们既要充分发挥空间想象能力,也要多动手去画一画、剪一剪、折一折.
不同
_ _ _ _
圆锥
四棱锥
圆柱
3.如图,几个图形是一些常见的几何体的展开图,请写出这些几何体的名称.
长方体
A B C D
4.【例1】沿圆柱体上底面直径截去一部分后的物体如图所示,从上面看到的图形是( )
D
小结:本题考查了从不同的方向观察物体.在解题时要注意,看得见的线画成实线,看不见的线画成虚线.
5.【例2】如图是由五个小立方体构成的立体图形,请你分别画出从它的正面、左面、上面三个方向看所得到的平面图形.
小结:画出从不同的方向看物体的形状的方法:首先观察物体,画出视图的外轮廓线,然后将视图补充完整.在画三种视图时,从正面、上面看到的图形要长对正,从正面、左面看到的图形要高平齐,从上面、左面看到的图形要宽相等.
_ _ _ _
圆柱
三棱柱
6.【例3】(人教7上P118、北师7上P11)如图是几种立体图形的展开图,请写出它们分别是哪种立体图形的展开图.
四棱锥
圆锥
小结:通过结合立体图形与平面图形的相互转化,理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
A.合 B.同
C.心 D.人
7.【例4】(跨学科融合)(2022河南)2022年北京冬奥会的奖牌“同心”表达了“天地合·人心同”的中华文化内涵.将这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,则在原正方体中,与“地”字所在面相对的面上的汉字是( )
D
小结:正方体的表面展开图中,相对的面之间一定相隔一个正方形,根据这一特点作答.
8.(人教7上P118、北师9上P137)如图,右面三幅图分别是从哪个方向看这个棱柱得到的?
解:(1)从上面看;(2)从正面看;(3)从左面看.
9.如图是由3个相同的小立方块搭成的几何体,请分别画出从正面、左面、上面看到的几何体的形状图.
A B C D
10.(2022临沂)如图所示的三棱柱的展开图不可能是( )
D
★11.(跨学科融合)2022年7月1日,香港回归祖国25周年.25年来,在祖国全力支持下,在香港特别行政区政府和社会各界共同努力下,“一国两制”实践在香港取得举世公认的成功.如图是一个正方体的六个面的展开图形(汉字和数字在正方体外部).
(1)“5”所对的面是 ;
(2)若将其折叠成正方体,如果“2”所在的面在底面,
“归”所在的面在后面,则上面是 ,前面是 ,
左面是 ;
(3)若将其折叠成正方体,“周”所在的面在前面,则上面不可能是 .
2
5
年
周
回
本课小结:
本节课主要学习了立体图形的折叠、展开与从不同方向观察立体图形,能将棱柱、圆柱、棱锥、圆锥的表面展开,也能将其表面展开图还原成立体图形,并且能画出从不同方向观察常见立体图形所得的三种视图.
教材P121习题4.1第4,6,7题
谢 谢
第四章 几何图形初步
立体图形与平面图形(2)
教学目标
【知识与技能】
(1)能从实物中抽象出几何图形,正确区分立体图形与平面图形;
(2)能把一些立体图形的问题转化为平面图形的问题进行研究和解决,探究平面图形与立体图形之间的关系
【过程与方法】
经历探究平面图形与立体图形之间的关系,发展空间观念,培养观察、分析、抽象、概括的能力以及动手操作的能力.
【情感态度与价值观】
通过本节课的数学活动,使学生养成主动探索、求知的学习态度,激发学生对数学知识的求知欲,并让学生体会数学活动中小组合作的重要性.
教学重难点
1熟悉常见的立体图形的表面展开图,并能根据立体图形的表面展开图还原立体图形;从不同方向观察立体图形得到的平面图形.
2由立体图形的表面展开图还原立体图形.
1.经历从不同方向观察物体的活动过程,初步体会从不同方向观察同一物体可能看到不一样的结果.
2.能画一些简单几何体以及由它们组成的简单组合体展开得到的平面图形.
3.(2022新课标)了解直棱柱、圆锥的侧面展开图,能根据展开图想象和制作模型.
知识点一:从不同方向看简单立体图形
(1)对于一些立体图形的问题,常把它们转化为平面图形来研究和处理.从不同方向看立体图形,往往会得到不同形状的平面图形.
(2)通常我们是从正面、 、 三个方向看,从而得到相应的平面图形.
上面
左面
例如:(人教7上P117)
(3)特别注意:画图时,要把看到的棱和顶点都画出来,例如:上图中从左面看的图和从上面看的图的棱要画出来.
1.(1)(人教7上P121、北师9上P135)如图,分别从正面、左面、上面观察这些立体图形,各能得到什么平面图形?
解:圆柱:长方形、长方形、圆;
圆锥:三角形、三角形、圆(带圆心);
球:圆、圆、圆.
A B C D
(2)(2022湖州)如图是由四个相同的小正方体组成的几何体,从正面看到的图形是( )
B
(3)如图,请在括号内填出是从什么方向看左边的立体图形得到的平面图形.
从正面看
从上面看
知识点二:立体图形的展开图
(1)有些 是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形.这样的平面图形称为相应立体图形的 .
(2)不是所有的 都可以展开成平面图形,例如:球体便不可以展开.
(3)同一立体图形按不同的方式展开,可以得到不同的平面
.
展开图
立体图形
展开图
立体图形
2.(1)(2022广元)如图是某几何体的展开图,该几何体是( )
A.长方体 B.圆柱
C.圆锥 D.三棱柱
B
A B C D
(2)(人教7上P119、北师7上P8-9)下列图形中,不是正方体的表面展开图的是( )
D
知识点三:平面图形的折叠
(1)同一立体图形沿不同方式展开,得到的平面展开图可能
;不同形状的平面图形经过折叠可能得到相同的立体图形.
(2)对于立体图形问题,我们既要充分发挥空间想象能力,也要多动手去画一画、剪一剪、折一折.
不同
_ _ _ _
圆锥
四棱锥
圆柱
3.如图,几个图形是一些常见的几何体的展开图,请写出这些几何体的名称.
长方体
A B C D
4.【例1】沿圆柱体上底面直径截去一部分后的物体如图所示,从上面看到的图形是( )
D
小结:本题考查了从不同的方向观察物体.在解题时要注意,看得见的线画成实线,看不见的线画成虚线.
5.【例2】如图是由五个小立方体构成的立体图形,请你分别画出从它的正面、左面、上面三个方向看所得到的平面图形.
小结:画出从不同的方向看物体的形状的方法:首先观察物体,画出视图的外轮廓线,然后将视图补充完整.在画三种视图时,从正面、上面看到的图形要长对正,从正面、左面看到的图形要高平齐,从上面、左面看到的图形要宽相等.
_ _ _ _
圆柱
三棱柱
6.【例3】(人教7上P118、北师7上P11)如图是几种立体图形的展开图,请写出它们分别是哪种立体图形的展开图.
四棱锥
圆锥
小结:通过结合立体图形与平面图形的相互转化,理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
A.合 B.同
C.心 D.人
7.【例4】(跨学科融合)(2022河南)2022年北京冬奥会的奖牌“同心”表达了“天地合·人心同”的中华文化内涵.将这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,则在原正方体中,与“地”字所在面相对的面上的汉字是( )
D
小结:正方体的表面展开图中,相对的面之间一定相隔一个正方形,根据这一特点作答.
8.(人教7上P118、北师9上P137)如图,右面三幅图分别是从哪个方向看这个棱柱得到的?
解:(1)从上面看;(2)从正面看;(3)从左面看.
9.如图是由3个相同的小立方块搭成的几何体,请分别画出从正面、左面、上面看到的几何体的形状图.
A B C D
10.(2022临沂)如图所示的三棱柱的展开图不可能是( )
D
★11.(跨学科融合)2022年7月1日,香港回归祖国25周年.25年来,在祖国全力支持下,在香港特别行政区政府和社会各界共同努力下,“一国两制”实践在香港取得举世公认的成功.如图是一个正方体的六个面的展开图形(汉字和数字在正方体外部).
(1)“5”所对的面是 ;
(2)若将其折叠成正方体,如果“2”所在的面在底面,
“归”所在的面在后面,则上面是 ,前面是 ,
左面是 ;
(3)若将其折叠成正方体,“周”所在的面在前面,则上面不可能是 .
2
5
年
周
回
本课小结:
本节课主要学习了立体图形的折叠、展开与从不同方向观察立体图形,能将棱柱、圆柱、棱锥、圆锥的表面展开,也能将其表面展开图还原成立体图形,并且能画出从不同方向观察常见立体图形所得的三种视图.
教材P121习题4.1第4,6,7题
谢 谢
