沪科版数学九年级上册 21.4 二次函数的应用(第1课时)同步练习(含解析)
文档属性
| 名称 | 沪科版数学九年级上册 21.4 二次函数的应用(第1课时)同步练习(含解析) | 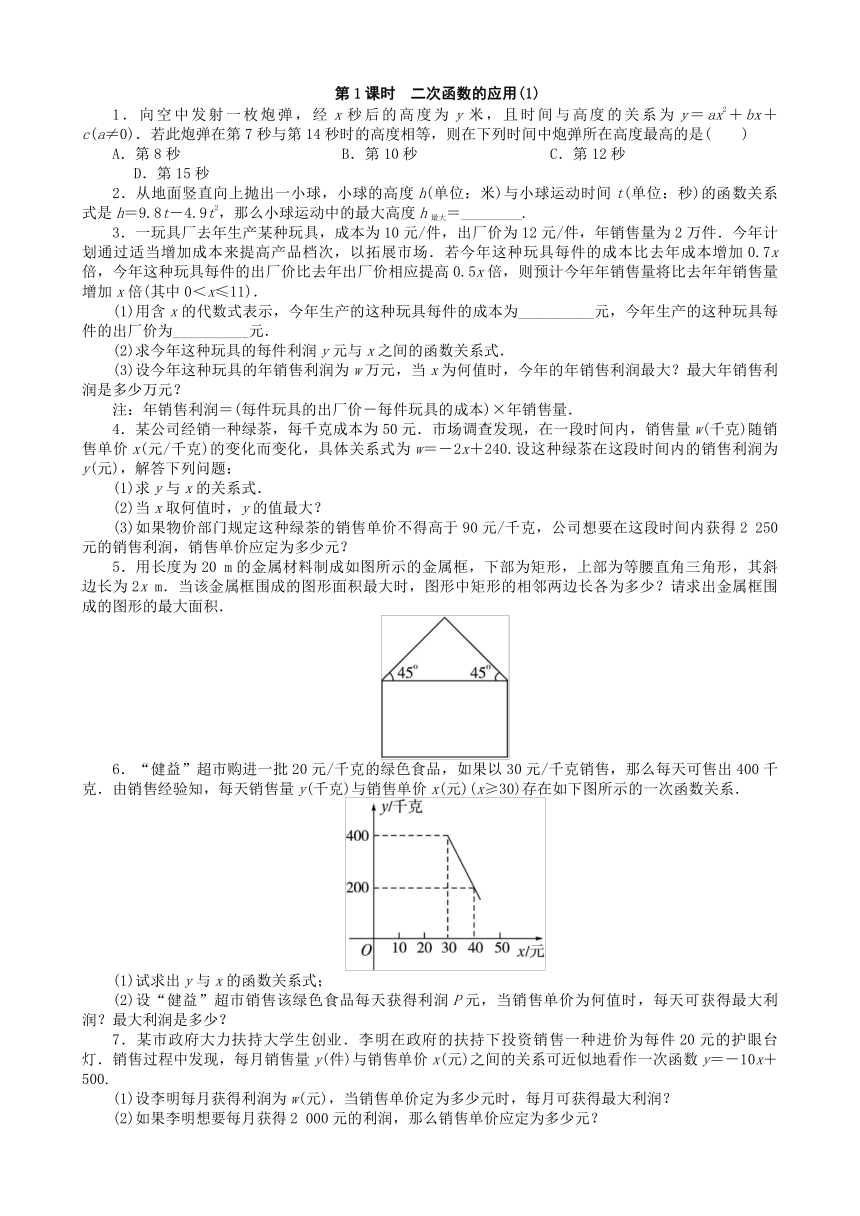 | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-28 17:44:21 | ||
图片预览


文档简介
第1课时 二次函数的应用(1)
1.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2+bx+c(a≠0).若此炮弹在第7秒与第14秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
2.从地面竖直向上抛出一小球,小球的高度h(单位:米)与小球运动时间t(单位:秒)的函数关系式是h=9.8t-4.9t2,那么小球运动中的最大高度h最大=________.
3.一玩具厂去年生产某种玩具,成本为10元/件,出厂价为12元/件,年销售量为2万件.今年计划通过适当增加成本来提高产品档次,以拓展市场.若今年这种玩具每件的成本比去年成本增加0.7x倍,今年这种玩具每件的出厂价比去年出厂价相应提高0.5x倍,则预计今年年销售量将比去年年销售量增加x倍(其中0<x≤11).
(1)用含x的代数式表示,今年生产的这种玩具每件的成本为__________元,今年生产的这种玩具每件的出厂价为__________元.
(2)求今年这种玩具的每件利润y元与x之间的函数关系式.
(3)设今年这种玩具的年销售利润为w万元,当x为何值时,今年的年销售利润最大?最大年销售利润是多少万元?
注:年销售利润=(每件玩具的出厂价-每件玩具的成本)×年销售量.
4.某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为w=-2x+240.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x的关系式.
(2)当x取何值时,y的值最大?
(3)如果物价部门规定这种绿茶的销售单价不得高于90元/千克,公司想要在这段时间内获得2 250元的销售利润,销售单价应定为多少元?
5.用长度为20 m的金属材料制成如图所示的金属框,下部为矩形,上部为等腰直角三角形,其斜边长为2x m.当该金属框围成的图形面积最大时,图形中矩形的相邻两边长各为多少?请求出金属框围成的图形的最大面积.
6.“健益”超市购进一批20元/千克的绿色食品,如果以30元/千克销售,那么每天可售出400千克.由销售经验知,每天销售量y(千克)与销售单价x(元)(x≥30)存在如下图所示的一次函数关系.
(1)试求出y与x的函数关系式;
(2)设“健益”超市销售该绿色食品每天获得利润P元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
7.某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数y=-10x+500.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2 000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2 000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
8.(创新应用)农民张大伯为了致富奔小康,大力发展家庭养殖业.他准备用40 m长的木栏围一个矩形的羊圈,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长25 m的墙,设计了如图所示的一个矩形羊圈.
(1)请你求出张大伯的矩形羊圈的面积;
(2)请你判断他的设计方案是否合理?如果合理,直接答合理;如果不合理又该如何设计?并说明理由.
参考答案
1. 解析:由题意可知,抛物线y=ax2+bx+c的对称轴为x=10.5,且a<0.又因为x=10秒离对称轴较近,当x=10秒时,y最大.
答案:B
2. 答案:4.9米
3. 解:(1)①10+7x ②12+6x
(2)y=(12+6x)-(10+7x)=2-x.
(3)∵w=2(1+x)(2-x)=-2x2+2x+4,
∴w=-2(x-0.5)2+4.5.
∵-2<0,0<x≤11,∴w有最大值.
∴当x=0.5时,w最大=4.5(万元).
答:当x为0.5时,今年的年销售利润最大,最大年销售利润是4.5万元.
4. 解:(1)y=(x-50)·w=(x-50)·(-2x+240)=-2x2+340x-12 000,∴y与x的关系式为y=-2x2+340x-12 000.
(2)y=-2x2+340x-12 000
=-2(x-85)2+2 450,
∴当x=85时,y的值最大.
(3)当y=2 250时,可得方程-2(x-85)2+2 450=2 250.解得x1=75,x2=95.
根据题意,x2=95不合题意应舍去.
∴当销售单价为75元时,可获得销售利润2 250元.
5. 解:根据题意可得:等腰直角三角形的直角边长为 m,矩形的一边长为2x m.
其相邻边长为=10-(2+)x.
所以该金属框围成的面积S=2x·[10-(2+)x]+=-(3+)x2+20x(0<x<10-).
当x==30-时,金属框围成的面积最大,此时矩形的一边长2x=60-(m),
相邻边长为10-(2+)×10(3-)=-10(m),S最大=100(3-)=300-(m2).
6. 解:(1)设y=kx+b,由图象知
解得∴y=-20x+1 000(30≤x≤50).
(2)P=(x-20)y=(x-20)(-20x+1 000)
=-20x2+1 400x-20 000.
∵-20<0,∴P有最大值.
当x==35时,P最大值=-20×352+1 400×35-20 000=4 500,
即当销售单价为35元/千克时,每天可获得最大利润4 500元.
7. 解:(1)由题意,得w=(x-20)·y=(x-20)·(-10x+500)=-10x2+700x-10 000.
x==35.
答:当销售单价定为35元时,每月可获得最大利润.
(2)由题意,得-10x2+700x-10 000=2 000.
解这个方程得x1=30,x2=40.
答:李明想要每月获得2 000元的利润,销售单价应定为30元或40元.
(3)∵a=-10<0,∴抛物线开口向下.
∴当30≤x≤40时,w≥2 000.
∵x≤32,∴当30≤x≤32时,w≥2 000.
设成本为P(元),由题意,得
P=20(-10x+500)=-200x+10 000.
∵k=-200<0,∴P随x的增大而减小.
∴当x=32时,P最小=3 600.
答:想要每月获得的利润不低于2 000元,每月的成本最少为3 600元.
8. 解:(1)40-25=15,故矩形的宽为 m.
∴S矩形ABCD=×25=187.5(m2).
(2)不合理.理由是:设利用x m的墙作为矩形羊圈的长,则宽为 m,设矩形的面积为y m2,
则y=x·=+20x
=(x-20)2+200.
∵<0,∴当x=20时,y最大=200.
∵200>187.5,故张大伯的设计不合理,应利用20 m墙,设计长为20 m,宽为10 m的矩形羊圈.
1.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2+bx+c(a≠0).若此炮弹在第7秒与第14秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
2.从地面竖直向上抛出一小球,小球的高度h(单位:米)与小球运动时间t(单位:秒)的函数关系式是h=9.8t-4.9t2,那么小球运动中的最大高度h最大=________.
3.一玩具厂去年生产某种玩具,成本为10元/件,出厂价为12元/件,年销售量为2万件.今年计划通过适当增加成本来提高产品档次,以拓展市场.若今年这种玩具每件的成本比去年成本增加0.7x倍,今年这种玩具每件的出厂价比去年出厂价相应提高0.5x倍,则预计今年年销售量将比去年年销售量增加x倍(其中0<x≤11).
(1)用含x的代数式表示,今年生产的这种玩具每件的成本为__________元,今年生产的这种玩具每件的出厂价为__________元.
(2)求今年这种玩具的每件利润y元与x之间的函数关系式.
(3)设今年这种玩具的年销售利润为w万元,当x为何值时,今年的年销售利润最大?最大年销售利润是多少万元?
注:年销售利润=(每件玩具的出厂价-每件玩具的成本)×年销售量.
4.某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为w=-2x+240.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x的关系式.
(2)当x取何值时,y的值最大?
(3)如果物价部门规定这种绿茶的销售单价不得高于90元/千克,公司想要在这段时间内获得2 250元的销售利润,销售单价应定为多少元?
5.用长度为20 m的金属材料制成如图所示的金属框,下部为矩形,上部为等腰直角三角形,其斜边长为2x m.当该金属框围成的图形面积最大时,图形中矩形的相邻两边长各为多少?请求出金属框围成的图形的最大面积.
6.“健益”超市购进一批20元/千克的绿色食品,如果以30元/千克销售,那么每天可售出400千克.由销售经验知,每天销售量y(千克)与销售单价x(元)(x≥30)存在如下图所示的一次函数关系.
(1)试求出y与x的函数关系式;
(2)设“健益”超市销售该绿色食品每天获得利润P元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
7.某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数y=-10x+500.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2 000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2 000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
8.(创新应用)农民张大伯为了致富奔小康,大力发展家庭养殖业.他准备用40 m长的木栏围一个矩形的羊圈,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长25 m的墙,设计了如图所示的一个矩形羊圈.
(1)请你求出张大伯的矩形羊圈的面积;
(2)请你判断他的设计方案是否合理?如果合理,直接答合理;如果不合理又该如何设计?并说明理由.
参考答案
1. 解析:由题意可知,抛物线y=ax2+bx+c的对称轴为x=10.5,且a<0.又因为x=10秒离对称轴较近,当x=10秒时,y最大.
答案:B
2. 答案:4.9米
3. 解:(1)①10+7x ②12+6x
(2)y=(12+6x)-(10+7x)=2-x.
(3)∵w=2(1+x)(2-x)=-2x2+2x+4,
∴w=-2(x-0.5)2+4.5.
∵-2<0,0<x≤11,∴w有最大值.
∴当x=0.5时,w最大=4.5(万元).
答:当x为0.5时,今年的年销售利润最大,最大年销售利润是4.5万元.
4. 解:(1)y=(x-50)·w=(x-50)·(-2x+240)=-2x2+340x-12 000,∴y与x的关系式为y=-2x2+340x-12 000.
(2)y=-2x2+340x-12 000
=-2(x-85)2+2 450,
∴当x=85时,y的值最大.
(3)当y=2 250时,可得方程-2(x-85)2+2 450=2 250.解得x1=75,x2=95.
根据题意,x2=95不合题意应舍去.
∴当销售单价为75元时,可获得销售利润2 250元.
5. 解:根据题意可得:等腰直角三角形的直角边长为 m,矩形的一边长为2x m.
其相邻边长为=10-(2+)x.
所以该金属框围成的面积S=2x·[10-(2+)x]+=-(3+)x2+20x(0<x<10-).
当x==30-时,金属框围成的面积最大,此时矩形的一边长2x=60-(m),
相邻边长为10-(2+)×10(3-)=-10(m),S最大=100(3-)=300-(m2).
6. 解:(1)设y=kx+b,由图象知
解得∴y=-20x+1 000(30≤x≤50).
(2)P=(x-20)y=(x-20)(-20x+1 000)
=-20x2+1 400x-20 000.
∵-20<0,∴P有最大值.
当x==35时,P最大值=-20×352+1 400×35-20 000=4 500,
即当销售单价为35元/千克时,每天可获得最大利润4 500元.
7. 解:(1)由题意,得w=(x-20)·y=(x-20)·(-10x+500)=-10x2+700x-10 000.
x==35.
答:当销售单价定为35元时,每月可获得最大利润.
(2)由题意,得-10x2+700x-10 000=2 000.
解这个方程得x1=30,x2=40.
答:李明想要每月获得2 000元的利润,销售单价应定为30元或40元.
(3)∵a=-10<0,∴抛物线开口向下.
∴当30≤x≤40时,w≥2 000.
∵x≤32,∴当30≤x≤32时,w≥2 000.
设成本为P(元),由题意,得
P=20(-10x+500)=-200x+10 000.
∵k=-200<0,∴P随x的增大而减小.
∴当x=32时,P最小=3 600.
答:想要每月获得的利润不低于2 000元,每月的成本最少为3 600元.
8. 解:(1)40-25=15,故矩形的宽为 m.
∴S矩形ABCD=×25=187.5(m2).
(2)不合理.理由是:设利用x m的墙作为矩形羊圈的长,则宽为 m,设矩形的面积为y m2,
则y=x·=+20x
=(x-20)2+200.
∵<0,∴当x=20时,y最大=200.
∵200>187.5,故张大伯的设计不合理,应利用20 m墙,设计长为20 m,宽为10 m的矩形羊圈.
