人教版数学七年级上册 第四章 几何图形初步: 第53课时 直线、射线、线段(3)课件 17张PPT
文档属性
| 名称 | 人教版数学七年级上册 第四章 几何图形初步: 第53课时 直线、射线、线段(3)课件 17张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-28 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第四章 几何图形初步
第53课时
直线、射线、线段(3)
一
新课学习
二
例变稳中练
三
四基三级练
四
思维拓展练
1.把一条线段的长度平均分成________的______部分的点叫做这条线段的中点.
2.如果几个点把一条线段的长度平均分成相等的n部分,那么这几个点叫做这条线段的___________.
相等
两
n等分点
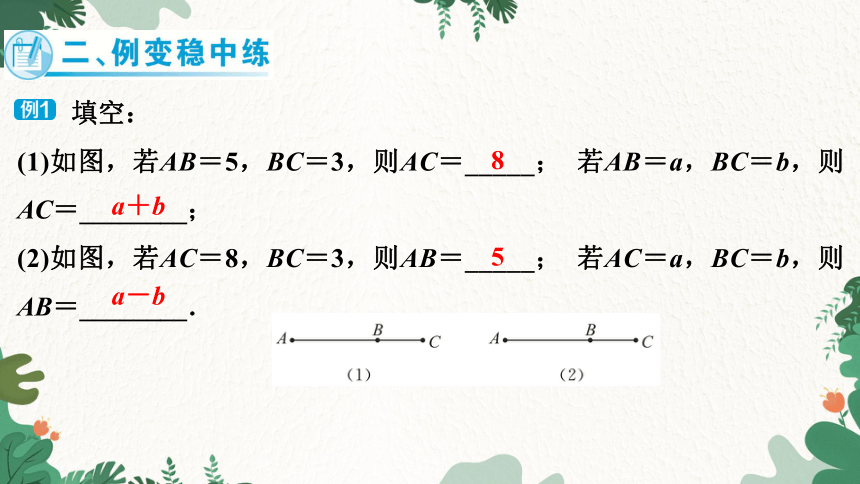
填空:
(1)如图,若AB=5,BC=3,则AC=_____; 若AB=a,BC=b,则AC=________;
(2)如图,若AC=8,BC=3,则AB=_____; 若AC=a,BC=b,则AB=________.
8
a+b
5
a-b
填空:
(1)如图,若AE=13,EC=5,则AC=______;
(2)如图,若AC=6,BC=4,则AB=_____.
18
2
点A,B,C在同一直线上,若AB=8,AC∶BC=3∶1,求线段AC的长度.
解:(1)当点C在线段AB上时,
∵AB=8,AC∶BC=3∶1,∴AC=6,
当点B在线段AC上时,
∵AB=8,AC∶BC=3∶1,∴BC=4,
∴AC=AB+BC=12.
如图,线段AB,点C是线段AB上一点,点M是AB的中点,点N是AC的中点.若AB=8 cm,AC=3.2 cm,求线段MN的长.
解:MN=AM-AN=4-1.6=2.4(cm).
如图,已知点C在线段AB上,线段AC=4,线段BC的长是线段AC长的两倍,点D是线段AB的中点,求线段CD的长.
解:∵AC=4,线段BC的长是线段AC长的两倍,
∴BC=8,
∴AB=AC+BC=12,
∵点D是线段AB的中点,
∴AD= AB=6,∴CD=AD-AC=2.
如图,线段AB=15 cm,且C点在AB上,BC= AC,D为BC的中点,求线段AD的长.
解:∵BC= AC,
∴设BC=2x,则AC=3x.∵D为BC的中点,
∴CD=BC=x,∵线段AB=15 cm,
∴AC+BC=5x=15,解得x=3(cm),
∴AD=3x+x=4x=12(cm).
一级
1.如图,点B是线段AC的中点.
(1)若AC=6 cm,则AB=_____cm;
(2)若AB=6 cm,则AC=______cm.
3
12
2.点M在线段AB上,给出下列四个条件,其中不能判定点M是线段AB中点的是( )
A.AM=BM B.AB=2AM
C.BM= AB D.AM+BM=AB
D
二级
3.如图,线段AB=10,点C在线段AB上,且AC∶BC=3∶2,点M是线段AC的中点,则BM=_____.
4.如图,C,D是线段AB上的两点,且点D是线段AC的中点,若AB=10 cm,BC=4 cm,则BD的长为________.
7
7 cm
三级
5.如图,线段AB=20,BC=15,点M是AC的中点.
(1)求线段AM的长度;
解:∵AB=20,BC=15,∴AC=AB-BC=20-15=5,又∵点M是AC的中点,
5.如图,线段AB=20,BC=15,点M是AC的中点.
(2)在CB上取一点N,使得CN∶NB=2∶3.求MN的长.
6.如图,点C为线段AD上一点,点B为CD的中点,且AD=8 cm,BD=1 cm,
(1)求AC的长;
解:∵点B为CD的中点,BD=1 cm,∴CD=2BD=2 cm,∵AD=8 cm,∴AC=AD-CD=8-2=6(cm).
(2)若点E在直线AD上,且EA=2 cm,求BE的长.
解:若点E在线段DA的延长线上,如答图1.
∵EA=2 cm,AD=8 cm,∴ED=EA+AD=2+8=10(cm),∵BD=1 cm,∴BE=ED-BD=10-1=9(cm),
若点E在线段AD上,如答图2,EA=2 cm,AD=8 cm.
∴ED=AD-EA=8-2=6(cm),∵BD=1 cm,∴BE=ED-BD=6-1=5(cm),
综上所述,BE的长为5 cm或9 cm.
谢谢大家!
第四章 几何图形初步
第53课时
直线、射线、线段(3)
一
新课学习
二
例变稳中练
三
四基三级练
四
思维拓展练
1.把一条线段的长度平均分成________的______部分的点叫做这条线段的中点.
2.如果几个点把一条线段的长度平均分成相等的n部分,那么这几个点叫做这条线段的___________.
相等
两
n等分点
填空:
(1)如图,若AB=5,BC=3,则AC=_____; 若AB=a,BC=b,则AC=________;
(2)如图,若AC=8,BC=3,则AB=_____; 若AC=a,BC=b,则AB=________.
8
a+b
5
a-b
填空:
(1)如图,若AE=13,EC=5,则AC=______;
(2)如图,若AC=6,BC=4,则AB=_____.
18
2
点A,B,C在同一直线上,若AB=8,AC∶BC=3∶1,求线段AC的长度.
解:(1)当点C在线段AB上时,
∵AB=8,AC∶BC=3∶1,∴AC=6,
当点B在线段AC上时,
∵AB=8,AC∶BC=3∶1,∴BC=4,
∴AC=AB+BC=12.
如图,线段AB,点C是线段AB上一点,点M是AB的中点,点N是AC的中点.若AB=8 cm,AC=3.2 cm,求线段MN的长.
解:MN=AM-AN=4-1.6=2.4(cm).
如图,已知点C在线段AB上,线段AC=4,线段BC的长是线段AC长的两倍,点D是线段AB的中点,求线段CD的长.
解:∵AC=4,线段BC的长是线段AC长的两倍,
∴BC=8,
∴AB=AC+BC=12,
∵点D是线段AB的中点,
∴AD= AB=6,∴CD=AD-AC=2.
如图,线段AB=15 cm,且C点在AB上,BC= AC,D为BC的中点,求线段AD的长.
解:∵BC= AC,
∴设BC=2x,则AC=3x.∵D为BC的中点,
∴CD=BC=x,∵线段AB=15 cm,
∴AC+BC=5x=15,解得x=3(cm),
∴AD=3x+x=4x=12(cm).
一级
1.如图,点B是线段AC的中点.
(1)若AC=6 cm,则AB=_____cm;
(2)若AB=6 cm,则AC=______cm.
3
12
2.点M在线段AB上,给出下列四个条件,其中不能判定点M是线段AB中点的是( )
A.AM=BM B.AB=2AM
C.BM= AB D.AM+BM=AB
D
二级
3.如图,线段AB=10,点C在线段AB上,且AC∶BC=3∶2,点M是线段AC的中点,则BM=_____.
4.如图,C,D是线段AB上的两点,且点D是线段AC的中点,若AB=10 cm,BC=4 cm,则BD的长为________.
7
7 cm
三级
5.如图,线段AB=20,BC=15,点M是AC的中点.
(1)求线段AM的长度;
解:∵AB=20,BC=15,∴AC=AB-BC=20-15=5,又∵点M是AC的中点,
5.如图,线段AB=20,BC=15,点M是AC的中点.
(2)在CB上取一点N,使得CN∶NB=2∶3.求MN的长.
6.如图,点C为线段AD上一点,点B为CD的中点,且AD=8 cm,BD=1 cm,
(1)求AC的长;
解:∵点B为CD的中点,BD=1 cm,∴CD=2BD=2 cm,∵AD=8 cm,∴AC=AD-CD=8-2=6(cm).
(2)若点E在直线AD上,且EA=2 cm,求BE的长.
解:若点E在线段DA的延长线上,如答图1.
∵EA=2 cm,AD=8 cm,∴ED=EA+AD=2+8=10(cm),∵BD=1 cm,∴BE=ED-BD=10-1=9(cm),
若点E在线段AD上,如答图2,EA=2 cm,AD=8 cm.
∴ED=AD-EA=8-2=6(cm),∵BD=1 cm,∴BE=ED-BD=6-1=5(cm),
综上所述,BE的长为5 cm或9 cm.
谢谢大家!
