多边形[下学期]

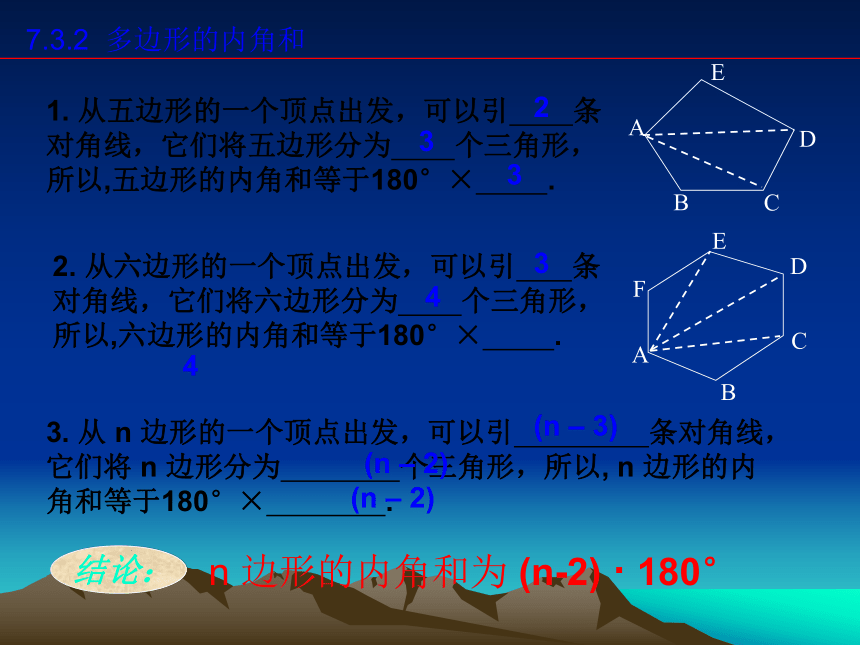
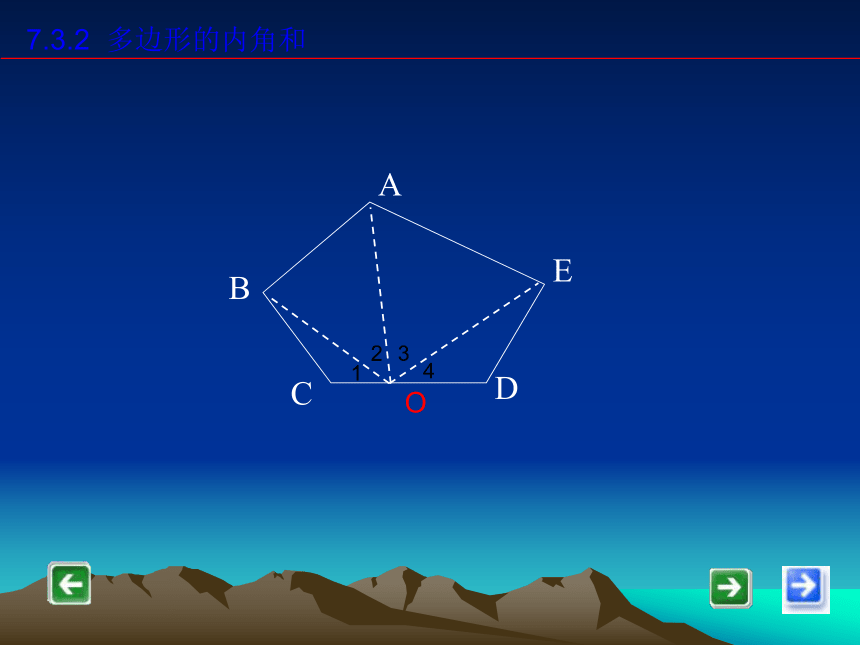
课件25张PPT。7.3.2多边形的内角和 上节课我们认识了多边形，还认识了多边形的内角，外角和对角线。大家还记得四边形，五边形，六边形的内角和、外角和分别是多少度吗？它们从一点出发有几条对角线呢？探究多边形的内角和 上节课我们利用测量的方法知道几个特殊多边形的内角和和外角和，你们又知道为什么它们的内角和和外角和是这些度数吗？一个n边形的内角和和外角和又是多少呢？7.3.2 多边形的内角和一般的四边形的内角和是多少度呢任意一个四边形的内角和都等于360°.试一试 画出任意一个四边形的一条对角线，都能将这个四边形分为两个三角形。这样，任意一个四边形的内角和都等于两个三角形的内角和，即360°。 请用同样的方法得出五边形，六边形和n边形的内角和吗？试一试。1. 从五边形的一个顶点出发，可以引 条对角线，它们将五边形分为 个三角形，所以,五边形的内角和等于180°× .2332. 从六边形的一个顶点出发，可以引 条对角线，它们将六边形分为 个三角形，所以,六边形的内角和等于180°× .(n – 3)443. 从 n 边形的一个顶点出发，可以引 条对角线，它们将 n 边形分为 个三角形，所以, n 边形的内角和等于180°× .7.3.2 多边形的内角和3(n – 2)(n – 2)n 边形的内角和为 (n-2) · 180° 结论：再试一试 把一多边形分成几个三角形，还有其它的分法吗？由新的分法，能得出多边形内角和公式吗？7.3.2 多边形的内角和O154327.3.2 多边形的内角和O12347.3.2 多边形的内角和O15432O1234结论n边形内角和等于(n-2)·180°。7.3.2 多边形的内角和小练习：（2）七边形的内角和等于 度.填空题：900（7－2）×180（3）一个多边形的内角和等于720 °，
那么这个多边形是 边形.六（4）如果一个四边形的一组对角互补，
那么另一组对角 .也互补（1）多边形的内角和随着边数的增加而 ，
边数增加一条时，它的内角和增加 度 .增 加1807.3.2 多边形的内角和解：如图，六边形ABCDEF中，
∠1+∠7=180 °，∠2+∠8=180 °，
∠3+∠9=180 °，∠4+∠10=180 °，
∠5+∠11=180 °，∠6+∠12=180 °.∵ ∠7+∠ 8+∠9+ ∠10 +∠11+ ∠12 =（6－2）×180 °= 720°, 结论：多边形的外角和等于360°.∴ ∠1+∠ 2+∠3+ ∠4 +∠5+ ∠6 = 6×180 °－720 ° = 360°.对于 n 边形，结论仍然成立！多边形的外角和等于360°7.3.2 多边形的内角和小练习：1. 判断题：（1）当多边形的边数增加时，它的外角和也随着增加 .（2）正六边形的每个外角都等于60度 .2. 填空题：（1）正九边形的每一个外角都等于 度. 40 （2）一个多边形的每一个外角都等于30°，
这个多边形是 边形. 正十二 课堂练习:1.一个多边形的外角都等于60°，这个多边形是n边形？ 解：因为多边形的外角和等于360°，所以根据题意，可知道这个多边形的边数是：
360÷60=6 .答:这个多边形是六边形. 2.下图是三个完全相同的正多边形拼成的无缝隙不重叠的图形的一部分，这种多边形是几边形？为什么？ 解：设：这个正多边形的一个内角为x°，
则由题图得：3x=360°. x=120°.
再根据多边形的内角和公式得：
n×120°=(n－2)×180°. 解得n=6 . 答:(略)练习1求下列图形中x的值：4、如图，五边形ABCDE的内角都相等，且∠1=∠2，∠3=∠4，求x的值。7.3.2 多边形的内角和（4）如果多边形的内角和等于外角和，
那么这个多边形是 边形。（1）八边形的内角和等于 度.（2）一个多边形的内角和等于1260° ，
这个多边形是 边形.1080九（3）一个多边形的每一个内角都等于135°，
则这个多边形是 边形.正八2.填空题：四你今天对多边形又知道了什么？n边形内角和等于(n-2)·180多边形的外角和等于360°n n-3n-23×18004×1800(n-2)×18001232344562×18003600360036003600再见