人教版九年级上册数学22.3实际问题与二次函数 同步训练(含答案)
文档属性
| 名称 | 人教版九年级上册数学22.3实际问题与二次函数 同步训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 172.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 20:25:42 | ||
图片预览



文档简介
人教版九年级上册数学22.3实际问题与二次函数同步训练
一、单选题
1.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为、若此炮弹在第8秒与第16秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
2.飞机着陆后滑行的距离(单位:米)关于滑行时间(单位,秒)的函数解析式是.在飞机着陆滑行中,最后6秒滑行的距离为( )米.
A.24 B.36 C.48 D.54
3.某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )
A. B. C. D.
4.向空中发射一枚炮弹,第x秒时的高度为y米,且高度与时间的关系为y=ax2+bx+c(a≠0).若此炮弹在第6秒与第18秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
5.如图是一个不倒翁的部分剖面图,可看做一个抛物线,若肚子最大的宽度,,按图示位置建立的平面直角坐标系可知,抛物线表达式为( )
A. B. C. D.
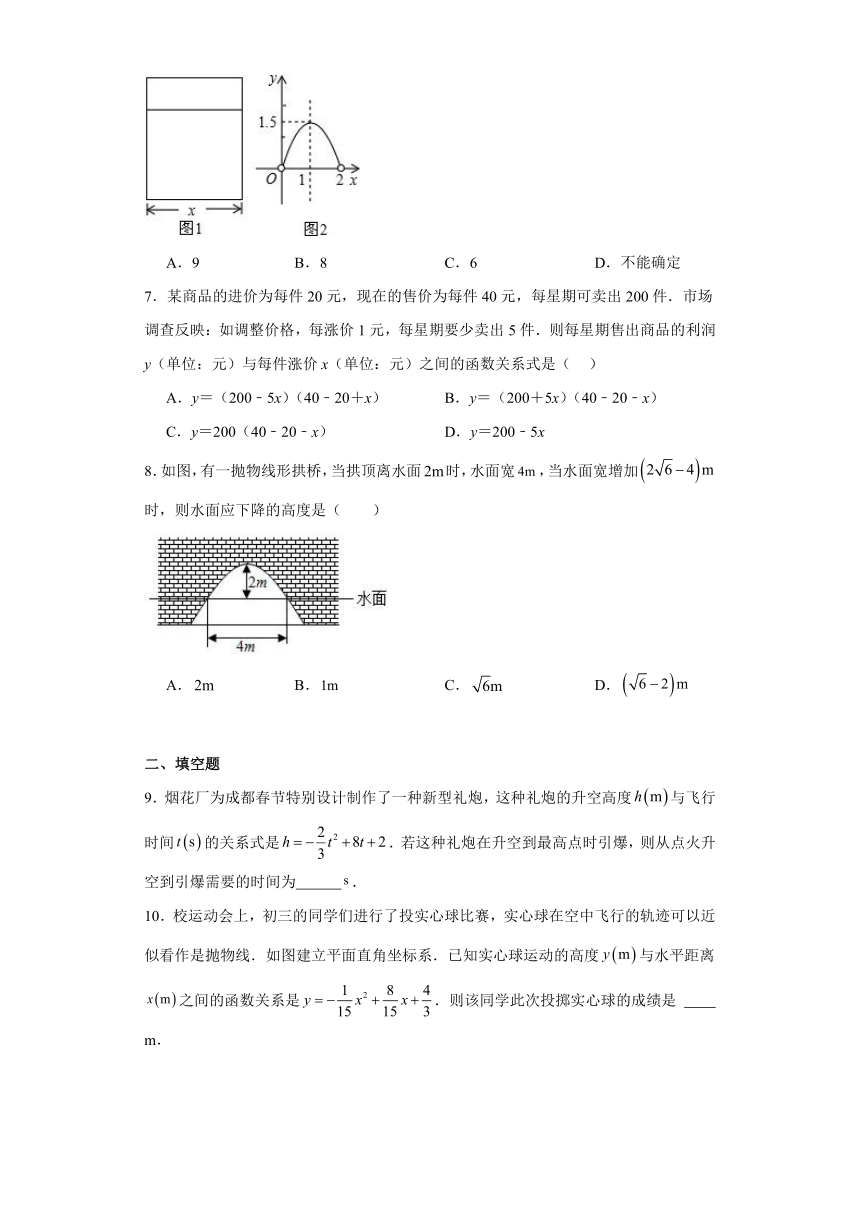
6.用总长为a米的材料做成如图1的矩形窗框,设窗框的宽为x米,窗框的面积为y米2,y关于x的函数图象如图2,则a的值是( )
A.9 B.8 C.6 D.不能确定
7.某商品的进价为每件20元,现在的售价为每件40元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出5件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )
A.y=(200﹣5x)(40﹣20+x) B.y=(200+5x)(40﹣20﹣x)
C.y=200(40﹣20﹣x) D.y=200﹣5x
8.如图,有一抛物线形拱桥,当拱顶离水面时,水面宽,当水面宽增加时,则水面应下降的高度是( )
A. B. C. D.
二、填空题
9.烟花厂为成都春节特别设计制作了一种新型礼炮,这种礼炮的升空高度与飞行时间的关系式是.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为 .
10.校运动会上,初三的同学们进行了投实心球比赛,实心球在空中飞行的轨迹可以近似看作是抛物线.如图建立平面直角坐标系.已知实心球运动的高度与水平距离之间的函数关系是.则该同学此次投掷实心球的成绩是 m.
11.飞机着陆后滑行的距离s(单位:米)与滑行的时间t(单位:秒)之间的函数关系式是,飞机着陆后滑行 秒才能停下来.
12.已知烟花弹爆炸后某个残片的空中飞行轨迹可以看成为二次函数图像的一部分,其中x为爆炸后经过的时间(秒),y为残片离地面的高度(米),请问在爆炸后1秒到6秒之间,残片距离地面的高度范围为 .
13.如图,某农场要盖一排三间同样大小的长方形的羊圈,打算一面利用旧墙,其余各面用木材围成栅栏,栅栏的总长为,设羊圈的总面积为,垂直于墙的一边长为,则S关于x的函数关系式为 .(不必写出自变量的取值范围)
14.如图是抛物线型拱桥截面,当拱顶离水面4时,水面宽6.若水面上升1,则水面宽度为 .
15.小燕去参观一个蔬菜大棚,大棚横截面为抛物线,有关数据如图所示,已知小燕的身高1.40米,在她不弯腰的情况下,横向活动范围有 米.
16.篮球联赛中,每两个球队之间进行两场比赛,设有x个球队参赛计划共打y场比赛,则y与x之间的函数关系为 .
三、解答题
17.某矩形工艺品长,宽,中间镶有宽度相同的三条丝绸花边.
(1)若丝绸花边的面积为,求丝绸花边的宽度.
(2)已知该工艺品的成本是元/件,如果以单价元/件销售,那么每天可售出件,另每天除工艺品的成本外所需支付的其它各种费用是元,根据销售经验,如果将销售单价每涨元,每天可少售出件,请问应该把销售单价定为多少元,能使每天所获利润最大?最大利润是多少元?
18.某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元,请用x的代数式来表示销售该品牌玩具获得利润______元.
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少.
19.某网店店主购进A,B两种型号的装饰链,其中A型装饰链的进货单价比B型装饰链的进货单价多20元,且消费500元购进A型装饰链的数量与消费400元购进B型装饰链的数量相等.销售中发现A型装饰链每月的销售量(个)与销售单价(元)之间满足的函数关系式为:;B型装饰链每月的销售量(个)与销售单价(元)之间满足的函数关系式为.
(1)求A,B两种型号装饰链的进货单价.
(2)已知A型装饰链的销售单价比B型装饰链的销售单价高20元,则当A,B两种型号装饰链的销售单价各为多少元时,每月销售这两种型号装饰链的总利润最大?并求出最大总利润.
20.某服装店销售一种T恤衫,每件进价为40元.经过市场调查,该T恤衫每周的销售量y(件)与销售单价x(元)之间满足如下的一次函数关系:当销售单价为60元时,每周的销售量为400件;当销售单价为80元时,每周的销售量为200件.
(1)求y与x之间的函数关系式.
(2)当销售单价定为多少时,该服装店每周销售这种T恤衫所获得的利润最大?最大利润是多少?
参考答案:
1.C
2.D
3.B
4.C
5.A
6.C
7.A
8.B
9.6
10.10
11.20
12./
13.
14.
15.
16.
17.(1)丝绸花边的宽度为;
(2)每件工艺品的销售单价定为元时,每天获得的利润最大,最大利润是元.
18.(1)
(2)销售价应定为50元或80元
(3)最大利润是8640元
19.(1)A型装饰链的进货单价为100元,B型装饰链的进货单价为80元
(2)当A型装饰链的销售单价140元,B型装饰链的销售单价120元时,每月销售这两种装饰链的总利润最大,最大总利润是3200元
20.(1);
(2)销售单价定为70元时,服装店每周销售这种T恤衫所获得的利润最大,最大利润是9000元.
答案第2页,共2页
一、单选题
1.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为、若此炮弹在第8秒与第16秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
2.飞机着陆后滑行的距离(单位:米)关于滑行时间(单位,秒)的函数解析式是.在飞机着陆滑行中,最后6秒滑行的距离为( )米.
A.24 B.36 C.48 D.54
3.某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )
A. B. C. D.
4.向空中发射一枚炮弹,第x秒时的高度为y米,且高度与时间的关系为y=ax2+bx+c(a≠0).若此炮弹在第6秒与第18秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
5.如图是一个不倒翁的部分剖面图,可看做一个抛物线,若肚子最大的宽度,,按图示位置建立的平面直角坐标系可知,抛物线表达式为( )
A. B. C. D.
6.用总长为a米的材料做成如图1的矩形窗框,设窗框的宽为x米,窗框的面积为y米2,y关于x的函数图象如图2,则a的值是( )
A.9 B.8 C.6 D.不能确定
7.某商品的进价为每件20元,现在的售价为每件40元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出5件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )
A.y=(200﹣5x)(40﹣20+x) B.y=(200+5x)(40﹣20﹣x)
C.y=200(40﹣20﹣x) D.y=200﹣5x
8.如图,有一抛物线形拱桥,当拱顶离水面时,水面宽,当水面宽增加时,则水面应下降的高度是( )
A. B. C. D.
二、填空题
9.烟花厂为成都春节特别设计制作了一种新型礼炮,这种礼炮的升空高度与飞行时间的关系式是.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为 .
10.校运动会上,初三的同学们进行了投实心球比赛,实心球在空中飞行的轨迹可以近似看作是抛物线.如图建立平面直角坐标系.已知实心球运动的高度与水平距离之间的函数关系是.则该同学此次投掷实心球的成绩是 m.
11.飞机着陆后滑行的距离s(单位:米)与滑行的时间t(单位:秒)之间的函数关系式是,飞机着陆后滑行 秒才能停下来.
12.已知烟花弹爆炸后某个残片的空中飞行轨迹可以看成为二次函数图像的一部分,其中x为爆炸后经过的时间(秒),y为残片离地面的高度(米),请问在爆炸后1秒到6秒之间,残片距离地面的高度范围为 .
13.如图,某农场要盖一排三间同样大小的长方形的羊圈,打算一面利用旧墙,其余各面用木材围成栅栏,栅栏的总长为,设羊圈的总面积为,垂直于墙的一边长为,则S关于x的函数关系式为 .(不必写出自变量的取值范围)
14.如图是抛物线型拱桥截面,当拱顶离水面4时,水面宽6.若水面上升1,则水面宽度为 .
15.小燕去参观一个蔬菜大棚,大棚横截面为抛物线,有关数据如图所示,已知小燕的身高1.40米,在她不弯腰的情况下,横向活动范围有 米.
16.篮球联赛中,每两个球队之间进行两场比赛,设有x个球队参赛计划共打y场比赛,则y与x之间的函数关系为 .
三、解答题
17.某矩形工艺品长,宽,中间镶有宽度相同的三条丝绸花边.
(1)若丝绸花边的面积为,求丝绸花边的宽度.
(2)已知该工艺品的成本是元/件,如果以单价元/件销售,那么每天可售出件,另每天除工艺品的成本外所需支付的其它各种费用是元,根据销售经验,如果将销售单价每涨元,每天可少售出件,请问应该把销售单价定为多少元,能使每天所获利润最大?最大利润是多少元?
18.某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元,请用x的代数式来表示销售该品牌玩具获得利润______元.
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少.
19.某网店店主购进A,B两种型号的装饰链,其中A型装饰链的进货单价比B型装饰链的进货单价多20元,且消费500元购进A型装饰链的数量与消费400元购进B型装饰链的数量相等.销售中发现A型装饰链每月的销售量(个)与销售单价(元)之间满足的函数关系式为:;B型装饰链每月的销售量(个)与销售单价(元)之间满足的函数关系式为.
(1)求A,B两种型号装饰链的进货单价.
(2)已知A型装饰链的销售单价比B型装饰链的销售单价高20元,则当A,B两种型号装饰链的销售单价各为多少元时,每月销售这两种型号装饰链的总利润最大?并求出最大总利润.
20.某服装店销售一种T恤衫,每件进价为40元.经过市场调查,该T恤衫每周的销售量y(件)与销售单价x(元)之间满足如下的一次函数关系:当销售单价为60元时,每周的销售量为400件;当销售单价为80元时,每周的销售量为200件.
(1)求y与x之间的函数关系式.
(2)当销售单价定为多少时,该服装店每周销售这种T恤衫所获得的利润最大?最大利润是多少?
参考答案:
1.C
2.D
3.B
4.C
5.A
6.C
7.A
8.B
9.6
10.10
11.20
12./
13.
14.
15.
16.
17.(1)丝绸花边的宽度为;
(2)每件工艺品的销售单价定为元时,每天获得的利润最大,最大利润是元.
18.(1)
(2)销售价应定为50元或80元
(3)最大利润是8640元
19.(1)A型装饰链的进货单价为100元,B型装饰链的进货单价为80元
(2)当A型装饰链的销售单价140元,B型装饰链的销售单价120元时,每月销售这两种装饰链的总利润最大,最大总利润是3200元
20.(1);
(2)销售单价定为70元时,服装店每周销售这种T恤衫所获得的利润最大,最大利润是9000元.
答案第2页,共2页
同课章节目录
