多边形的内角和[下学期]
文档属性
| 名称 | 多边形的内角和[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 631.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-18 15:43:00 | ||
图片预览




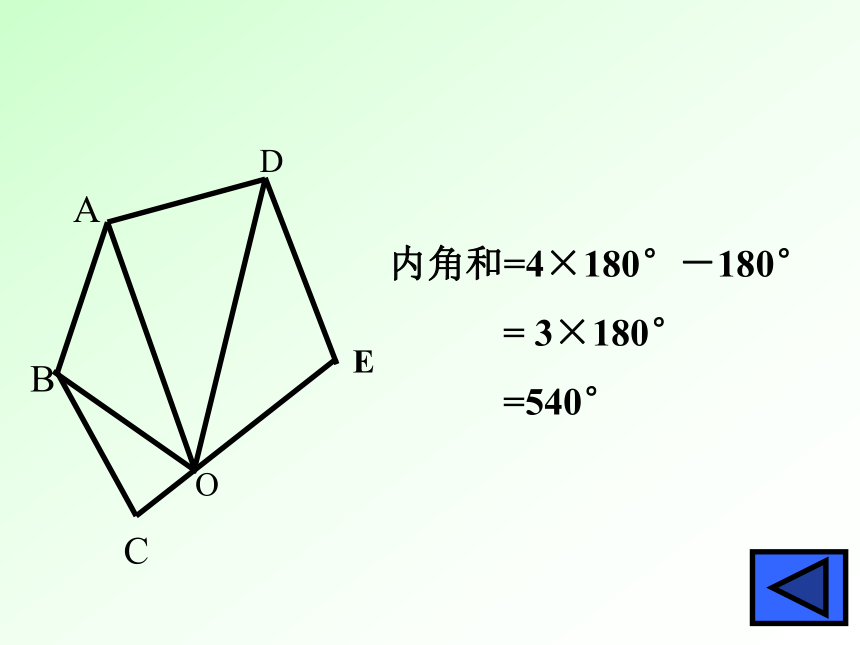


文档简介
课件33张PPT。欢迎光临 想设计一个内角和为2008的多边形图案以预祝2008年奥运会的胜利召开,这个的想法能实现吗??? ● §7.3.2多边形的内角和活动1:探究四边形的内角和活动2:探究多边形的内角和类似地你能否求出五边形的内角和呢?聪明的你,能想出几种方法呢?探索多边形的内角和这个六边形的内角和应该怎么求呢?
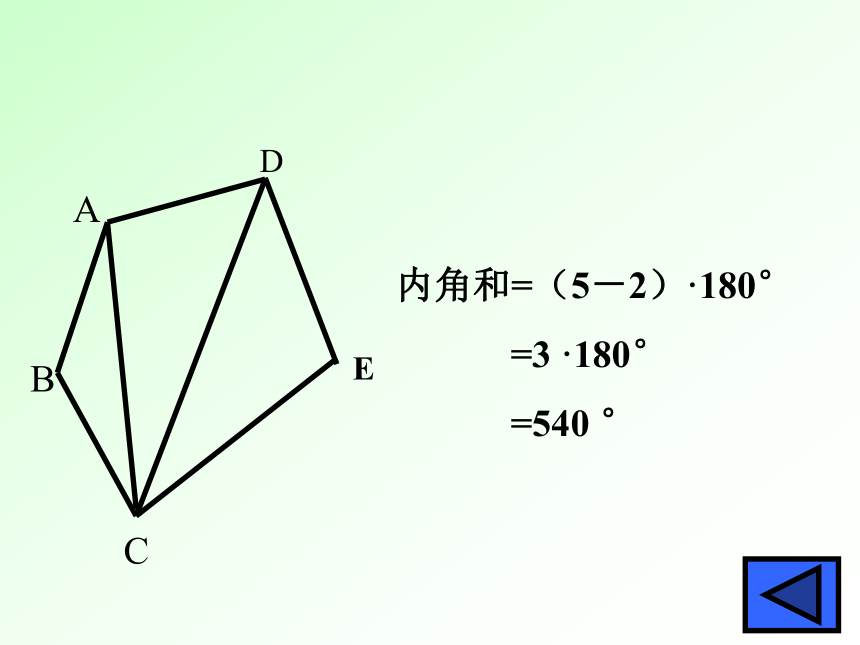
你有几种方法呢?ACDEB内角和=(5-2)·180°
=3 ·180°
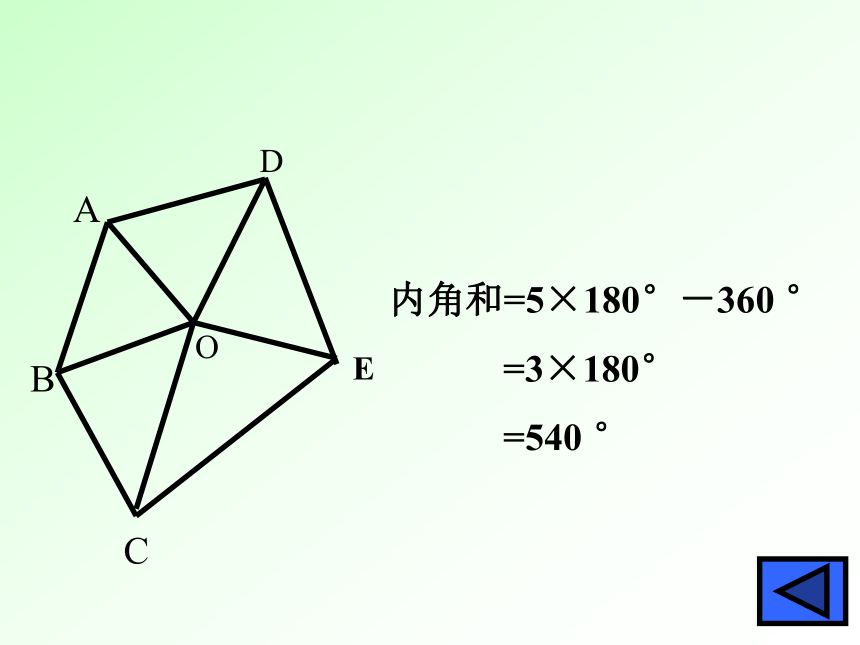
=540 °ACDEBO内角和=5×180°-360 °
=3×180°
=540 °ACDEBO内角和=4×180°-180°
= 3×180°
=540°小结:纵观上述方法,其共同点是
通过图形分割法,把五边形问题
转化为熟悉的三角形、四边形问
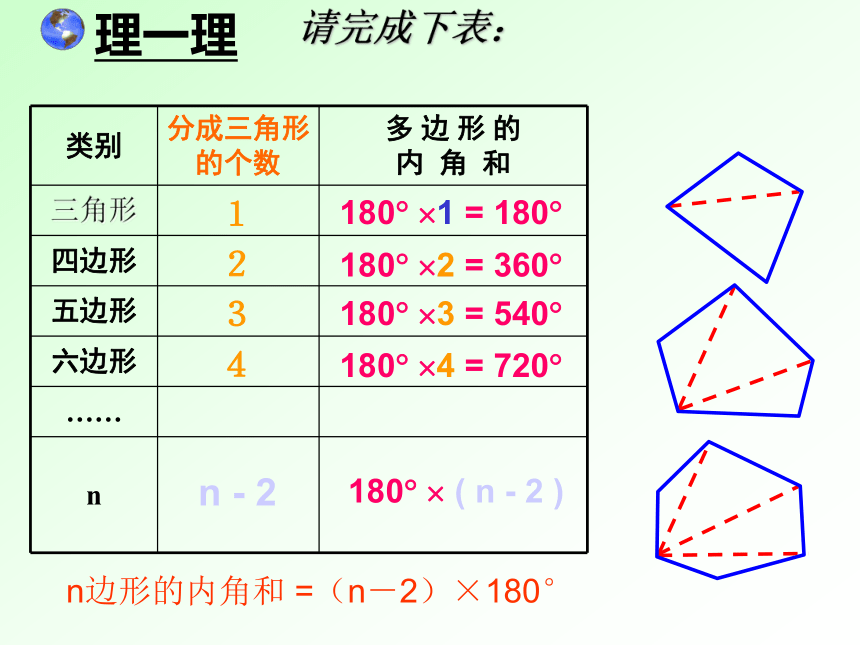
题来解决。?思考? 观察这些方法,有何共同点?请完成下表:3412180? ?1 = 180? 180? ?2 = 360? 180? ?3 = 540? 180? ?4 = 720? n - 2180? ? ( n - 2 ) n边形的内角和 =(n-2)×180° n边形的内角和 =(n-2)×180° 由此等式我们可以知道: 已知多边形的边数可以求出它的内角和,反之,已知多边形的内角和也可以求出它的边数。 想设计一个内角和为2008的多边形图案以预祝2008年奥运会的胜利召开,这个的想法能实现吗???思考? ● 比一比看谁答得快:1.十二边形的内角和是多少?1800°2.边数越多的多边形的内角和越__.大3.铺地板的六角砖内角和是多少度?720°4. 公园里的八角亭的内角和是多少度?1080°5. n边形内角和是1440° ,则n=__?10°6.六角螺母的一个面是六边形的,
这个六边形的六个内角相等,求每一个内角的度数。例题与练习例1:如果一个四边形的一组对角互 补,那么另一组对角有什么关系?解: 四边形ABCD中,
∠A +∠C = 180° ∵∠A +∠B +∠C +∠D =(4-2)×180°=360°
∴∠B +∠D =360°-(∠A +∠C)
=360°-180°
=180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。CDAB练习:1.求下列图形中x 的值. 140°x°x°120°150°2x°x°120°80°75°x°x°150°135°60°ABCDEAB∥CD(1)(2)(3)(4)学以致用:1:求下列图中x的值.2.十边形的内角和为 度,正八边形的内角和为 度。
3.多边形的边数增加1,内角和就增加 度;多边形的边数由7增加到10,内角和增加 度。
4.已知一个多边形的内角和为1620°,则它的边数为 。
5.每个内角都是108°的多边形是
边形. 例2: 如图,在六边形的顶点处各取一个外角,这些外角的和叫做六边形的外角和,六边形的外角和等于多少? 考虑以下问题: 1.任何一个外角同与它相邻的内角有什么关系?
2.六边形的6个外角加上与它们相邻的内角,所得的总和是多少?
3.上述总和与六边形的内角和、外角和有什么关系?
FABCDE543216解:六边形的外角和 = 总和-六边形的内角和
=6×180°-(6-2)×180°
=2×180°
=360° 想一想: n 边形的外角和是多少度呢?(n 的值是不小于3的任意整数) n边形的外角和= n ×180°-(n-2)×180°
=2×180°
=360° 由此可得: 多边形的外角和等于360° 活动4:探索多边形的外角和是多少呢?结论:任意多边形的外角和都为360.2.多边形外角和与内角和之间有什么关系?
(1)各内角与相邻外角互补;(2)外角和=n个平角-内角和
=n×180°-(n-2) × 180°=360°(3)结论:n边形的外角和等于360°1、若一个多边形的边数增加1,
则它的内角和( );
它的外角和( ).A. 不变B. 增加900C. 增加1800D. 不能确定AC3、若一个四边形的四个内角的度数之比
为1∶3 ∶4 ∶2 ,求这四个内角的度数.解:设每一份内角为x,则四个内角的度数分别为x,3x,4x,2x则(4-2) ×180°=x+3x+4x+2x10x=360°x=36°这四个内角分别为360,1080,1440,720.2、已知一个多边形的内角和是外角和
的3倍,求这个多边形的边数.解:设这个多边形的边数为n,根据题意,得(n-2) ×180°=3×3600n-2=6n=8 量一量 ● 交流反思9、在四边形的四个内角中,最多有
几个钝角?最多能有几个锐角? 你学到了什么?归纳与小结 比一比15、已知一个多边形除了一个内角外,其余各内角的和是2750°,求这个多边形的边数。
16、 如图:我国的国旗上的五星是正五角星,正五角星中的五边形ABCDE是正五边形,你能求出五角星中∠F的度数?
DCBEA18F360 比一比14、如图:某居民小区搞绿化,分别在三角 形、四边形、五边形的广场各角修建半径为1米的花坛。小区绿化组长想先求花坛的面积,再根据面积买花苗。你能帮绿化组长求出花坛的面积吗?(结果保留π)3π 小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
ABCDE12345(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的? 小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:(1)小明每从一条街道转到下一条街道时,
身体转过的角是哪个角?ABCDE(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?FGHMN比一比,看谁做得准! 有一张长方形的桌面,它的四个内角和为360°,现在锯掉它的一个角,剩下残余桌面所有的内角和是多少?通过本节课的学习,你学到了哪些知识?有何体会?1、 在学习多边形的有关概念时,我们通过复习的有关概念来类比得出的,这种通过复习知识,比较、得出新知识的方法在以往的数学学习中也曾出现过。2、 我们在研究、探索多边形的内角和公式时,首先从具体的、特殊的四边形、五边形入手,来得出多边形的内角和公式。在研究问题的过程中,把多边形问题通过分割成三角形来研究,即把复杂问题转化为简单问题。
你有几种方法呢?ACDEB内角和=(5-2)·180°
=3 ·180°
=540 °ACDEBO内角和=5×180°-360 °
=3×180°
=540 °ACDEBO内角和=4×180°-180°
= 3×180°
=540°小结:纵观上述方法,其共同点是
通过图形分割法,把五边形问题
转化为熟悉的三角形、四边形问
题来解决。?思考? 观察这些方法,有何共同点?请完成下表:3412180? ?1 = 180? 180? ?2 = 360? 180? ?3 = 540? 180? ?4 = 720? n - 2180? ? ( n - 2 ) n边形的内角和 =(n-2)×180° n边形的内角和 =(n-2)×180° 由此等式我们可以知道: 已知多边形的边数可以求出它的内角和,反之,已知多边形的内角和也可以求出它的边数。 想设计一个内角和为2008的多边形图案以预祝2008年奥运会的胜利召开,这个的想法能实现吗???思考? ● 比一比看谁答得快:1.十二边形的内角和是多少?1800°2.边数越多的多边形的内角和越__.大3.铺地板的六角砖内角和是多少度?720°4. 公园里的八角亭的内角和是多少度?1080°5. n边形内角和是1440° ,则n=__?10°6.六角螺母的一个面是六边形的,
这个六边形的六个内角相等,求每一个内角的度数。例题与练习例1:如果一个四边形的一组对角互 补,那么另一组对角有什么关系?解: 四边形ABCD中,
∠A +∠C = 180° ∵∠A +∠B +∠C +∠D =(4-2)×180°=360°
∴∠B +∠D =360°-(∠A +∠C)
=360°-180°
=180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。CDAB练习:1.求下列图形中x 的值. 140°x°x°120°150°2x°x°120°80°75°x°x°150°135°60°ABCDEAB∥CD(1)(2)(3)(4)学以致用:1:求下列图中x的值.2.十边形的内角和为 度,正八边形的内角和为 度。
3.多边形的边数增加1,内角和就增加 度;多边形的边数由7增加到10,内角和增加 度。
4.已知一个多边形的内角和为1620°,则它的边数为 。
5.每个内角都是108°的多边形是
边形. 例2: 如图,在六边形的顶点处各取一个外角,这些外角的和叫做六边形的外角和,六边形的外角和等于多少? 考虑以下问题: 1.任何一个外角同与它相邻的内角有什么关系?
2.六边形的6个外角加上与它们相邻的内角,所得的总和是多少?
3.上述总和与六边形的内角和、外角和有什么关系?
FABCDE543216解:六边形的外角和 = 总和-六边形的内角和
=6×180°-(6-2)×180°
=2×180°
=360° 想一想: n 边形的外角和是多少度呢?(n 的值是不小于3的任意整数) n边形的外角和= n ×180°-(n-2)×180°
=2×180°
=360° 由此可得: 多边形的外角和等于360° 活动4:探索多边形的外角和是多少呢?结论:任意多边形的外角和都为360.2.多边形外角和与内角和之间有什么关系?
(1)各内角与相邻外角互补;(2)外角和=n个平角-内角和
=n×180°-(n-2) × 180°=360°(3)结论:n边形的外角和等于360°1、若一个多边形的边数增加1,
则它的内角和( );
它的外角和( ).A. 不变B. 增加900C. 增加1800D. 不能确定AC3、若一个四边形的四个内角的度数之比
为1∶3 ∶4 ∶2 ,求这四个内角的度数.解:设每一份内角为x,则四个内角的度数分别为x,3x,4x,2x则(4-2) ×180°=x+3x+4x+2x10x=360°x=36°这四个内角分别为360,1080,1440,720.2、已知一个多边形的内角和是外角和
的3倍,求这个多边形的边数.解:设这个多边形的边数为n,根据题意,得(n-2) ×180°=3×3600n-2=6n=8 量一量 ● 交流反思9、在四边形的四个内角中,最多有
几个钝角?最多能有几个锐角? 你学到了什么?归纳与小结 比一比15、已知一个多边形除了一个内角外,其余各内角的和是2750°,求这个多边形的边数。
16、 如图:我国的国旗上的五星是正五角星,正五角星中的五边形ABCDE是正五边形,你能求出五角星中∠F的度数?
DCBEA18F360 比一比14、如图:某居民小区搞绿化,分别在三角 形、四边形、五边形的广场各角修建半径为1米的花坛。小区绿化组长想先求花坛的面积,再根据面积买花苗。你能帮绿化组长求出花坛的面积吗?(结果保留π)3π 小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
ABCDE12345(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的? 小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:(1)小明每从一条街道转到下一条街道时,
身体转过的角是哪个角?ABCDE(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?FGHMN比一比,看谁做得准! 有一张长方形的桌面,它的四个内角和为360°,现在锯掉它的一个角,剩下残余桌面所有的内角和是多少?通过本节课的学习,你学到了哪些知识?有何体会?1、 在学习多边形的有关概念时,我们通过复习的有关概念来类比得出的,这种通过复习知识,比较、得出新知识的方法在以往的数学学习中也曾出现过。2、 我们在研究、探索多边形的内角和公式时,首先从具体的、特殊的四边形、五边形入手,来得出多边形的内角和公式。在研究问题的过程中,把多边形问题通过分割成三角形来研究,即把复杂问题转化为简单问题。
