《指数函数、对数函数和幂函数》单元测试
文档属性
| 名称 | 《指数函数、对数函数和幂函数》单元测试 |
|
|
| 格式 | zip | ||
| 文件大小 | 112.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-12 00:00:00 | ||
图片预览



文档简介
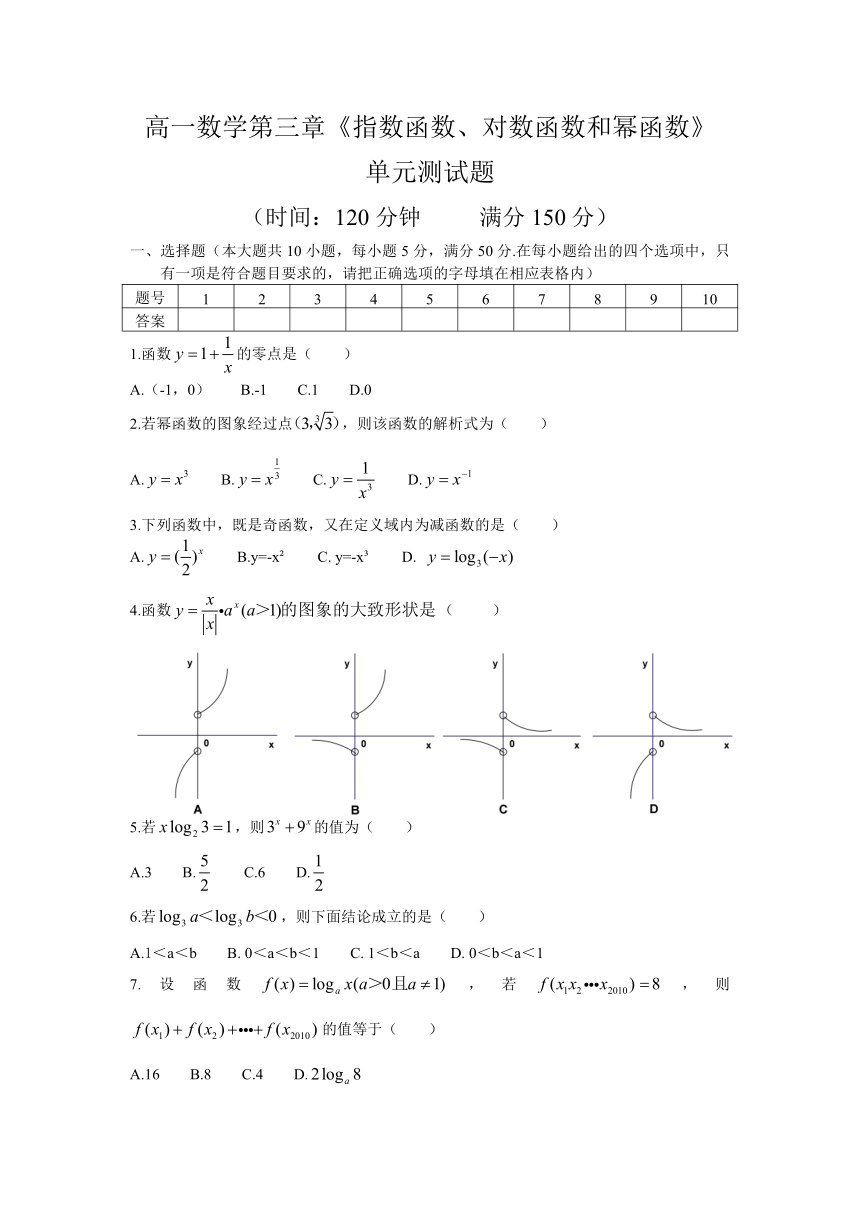
高一数学第三章《指数函数、对数函数和幂函数》
单元测试题
(时间:120分钟 满分150分)
选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确选项的字母填在相应表格内)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.函数的零点是( )
A.(-1,0) B.-1 C.1 D.0
2.若幂函数的图象经过点,则该函数的解析式为( )
A. B. C. D.
3.下列函数中,既是奇函数,又在定义域内为减函数的是( )
A. B.y=-x2 C. y=-x3 D.
4.函数( )
5.若,则的值为( )
A.3 B. C.6 D.
6.若,则下面结论成立的是( )
A.1<a<b B. 0<a<b<1 C. 1<b<a D. 0<b<a<1
7.设函数,若,则的值等于( )
A.16 B.8 C.4 D.
8.设,则之间的大小关系是( )
A. B.
C. D.
9.若0<x<y<1,则有( )
A. B. C. D.
10.函数在[0,1]上的最大值与最小值之和为a,则a的值为( )
A. B. C.2 D.4
二、填空题(本大题共4小题,每小题5分,满分20分.请把正确的答案填在相应的表格里)
题号
11
12
13
14
答案
11.设集合A={5,},B={a,b},若A∩B={2},则A∪B=________________.
12.已知函数是奇函数,则a=_____________________.
13.函数的值域是__________________________.
14.已知函数则=_________________.
三、解答题(本大题共6小题,满分80分.解答须写出必要的文字说明、证明过程和演算步骤)
15.(本题满分12分)如果(a>0且a≠1),求x得取值范围.
16(本题满分12分)设函数?(x)=x-ln(x+2),证明函数?(x)在内有两个零点.
17.(本题满分14分)设函数,若时,?(x)的最小值为-8,求a、b的值.
18.(本题满分14分)已知函数(a>0,且a≠1).
(1)求函数的定义域;
(2)求使?(x)>0的x的取值范围.
19.(本题满分14分)集合A是由具备下列性质的函数?(x)组成的:①函数?(x)的定义域是[0,+∞);②函数?(x)的值域是[-2,4);③函数?(x)在[0,+∞)上是增函数.
(1)判断是否属于集合A,并说明理由;
(2)对于(1)中你认为属于集合A的函数?(x),不等式?(x)+?(x+2)<2?(x+1)是否对于任意的x≥0总成立?若不成立,请证明你的结论.
20.(本题满分14分)如图,是A、B两辆汽车的速度随时间变化的关系.假设两辆汽车同时同地同向行驶.
(1)解释在时间0到1分钟时,A、B两辆车的速度变化情况:
(2)两辆车何时速度相等;
(3)A车在何时能追上B车?(备用知识:当速度v=at+b时,路程)
参考答案
1.B 【解析】由
2.B 【解析】设幂函数为,则,.
3.C 【解析】A、D不具有奇偶性,B是偶函数.
4.B 【解析】,其图象为B.
5.C 【解析】.
6.B 【解析】在(0,+∞)上是增函数,由已知得.
7.A 【解析】
.
8.C 【解析】,,,.
9.C 【解析】是增函数,.
10.B 【解析】函数与函数在[0,1]上具有相同的单调性,∴?(x)的最大值与最小值应在[0,1]的端点处取得,由,得.
11.{1,2,5}【解析】∵A∩B={2},∴2∈A,,,又2∈B,∴b=2.∴A∪B={1,2,5}.
12. 【解析】函数的定义域为R,∵?(x)是奇函数,∴?(0)=0,.
13.(-∞,-2) 【解析】∴此函数的值域是(-∞,-2).
14. 【解析】
.
15.解:当0当a>1时,由于,2x+1≤x-5,解得x≤-6.
综上所述,x的取值范围是:当当016.证明:∵?(x)=x-ln(x+2),∴
又∵函数?(x)在上的图象是连续的,
∴函数?(x)在内各有一个零点,即函数?(x)在有两个零点.
17.解:.当时,?(x)取得最小值,∴.
所求a、b的值分别为-2、-6.
18.解:(1)由∴函数的定义域为(0,+∞).
(2) ,当a>1时,
当0 综上,当019.解:(1)
对于,满足条件①.由x≥0,知,
∴满足条件②.
又在[0,+∞)上是减函数,在[0,+∞)上是增函数,满足条件③.
属于集合A.
(2)由(1)知属于集合A,,即
>0,对任意x≥0此式恒成立.∴原不等式对任意x≥0总成立.
20.解:(1)汽车A的速度从0千米/分钟增加到2千米/分钟,汽车B的速度从1千米/分钟增加到1.5千米/分钟.
(2)汽车A的速度,汽车B的速度.
由∴两车在分钟时速度相等.
(3)汽车的路程
当0≤t<1时,.
.
单元测试题
(时间:120分钟 满分150分)
选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确选项的字母填在相应表格内)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.函数的零点是( )
A.(-1,0) B.-1 C.1 D.0
2.若幂函数的图象经过点,则该函数的解析式为( )
A. B. C. D.
3.下列函数中,既是奇函数,又在定义域内为减函数的是( )
A. B.y=-x2 C. y=-x3 D.
4.函数( )
5.若,则的值为( )
A.3 B. C.6 D.
6.若,则下面结论成立的是( )
A.1<a<b B. 0<a<b<1 C. 1<b<a D. 0<b<a<1
7.设函数,若,则的值等于( )
A.16 B.8 C.4 D.
8.设,则之间的大小关系是( )
A. B.
C. D.
9.若0<x<y<1,则有( )
A. B. C. D.
10.函数在[0,1]上的最大值与最小值之和为a,则a的值为( )
A. B. C.2 D.4
二、填空题(本大题共4小题,每小题5分,满分20分.请把正确的答案填在相应的表格里)
题号
11
12
13
14
答案
11.设集合A={5,},B={a,b},若A∩B={2},则A∪B=________________.
12.已知函数是奇函数,则a=_____________________.
13.函数的值域是__________________________.
14.已知函数则=_________________.
三、解答题(本大题共6小题,满分80分.解答须写出必要的文字说明、证明过程和演算步骤)
15.(本题满分12分)如果(a>0且a≠1),求x得取值范围.
16(本题满分12分)设函数?(x)=x-ln(x+2),证明函数?(x)在内有两个零点.
17.(本题满分14分)设函数,若时,?(x)的最小值为-8,求a、b的值.
18.(本题满分14分)已知函数(a>0,且a≠1).
(1)求函数的定义域;
(2)求使?(x)>0的x的取值范围.
19.(本题满分14分)集合A是由具备下列性质的函数?(x)组成的:①函数?(x)的定义域是[0,+∞);②函数?(x)的值域是[-2,4);③函数?(x)在[0,+∞)上是增函数.
(1)判断是否属于集合A,并说明理由;
(2)对于(1)中你认为属于集合A的函数?(x),不等式?(x)+?(x+2)<2?(x+1)是否对于任意的x≥0总成立?若不成立,请证明你的结论.
20.(本题满分14分)如图,是A、B两辆汽车的速度随时间变化的关系.假设两辆汽车同时同地同向行驶.
(1)解释在时间0到1分钟时,A、B两辆车的速度变化情况:
(2)两辆车何时速度相等;
(3)A车在何时能追上B车?(备用知识:当速度v=at+b时,路程)
参考答案
1.B 【解析】由
2.B 【解析】设幂函数为,则,.
3.C 【解析】A、D不具有奇偶性,B是偶函数.
4.B 【解析】,其图象为B.
5.C 【解析】.
6.B 【解析】在(0,+∞)上是增函数,由已知得.
7.A 【解析】
.
8.C 【解析】,,,.
9.C 【解析】是增函数,.
10.B 【解析】函数与函数在[0,1]上具有相同的单调性,∴?(x)的最大值与最小值应在[0,1]的端点处取得,由,得.
11.{1,2,5}【解析】∵A∩B={2},∴2∈A,,,又2∈B,∴b=2.∴A∪B={1,2,5}.
12. 【解析】函数的定义域为R,∵?(x)是奇函数,∴?(0)=0,.
13.(-∞,-2) 【解析】∴此函数的值域是(-∞,-2).
14. 【解析】
.
15.解:当0
综上所述,x的取值范围是:当当0
又∵函数?(x)在上的图象是连续的,
∴函数?(x)在内各有一个零点,即函数?(x)在有两个零点.
17.解:.当时,?(x)取得最小值,∴.
所求a、b的值分别为-2、-6.
18.解:(1)由∴函数的定义域为(0,+∞).
(2) ,当a>1时,
当0
对于,满足条件①.由x≥0,知,
∴满足条件②.
又在[0,+∞)上是减函数,在[0,+∞)上是增函数,满足条件③.
属于集合A.
(2)由(1)知属于集合A,,即
>0,对任意x≥0此式恒成立.∴原不等式对任意x≥0总成立.
20.解:(1)汽车A的速度从0千米/分钟增加到2千米/分钟,汽车B的速度从1千米/分钟增加到1.5千米/分钟.
(2)汽车A的速度,汽车B的速度.
由∴两车在分钟时速度相等.
(3)汽车的路程
当0≤t<1时,.
.
