北师大版数学八年级上册5.7用二元一次方程确定一次函数表达式 导学案(含答案)
文档属性
| 名称 | 北师大版数学八年级上册5.7用二元一次方程确定一次函数表达式 导学案(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 184.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 06:47:47 | ||
图片预览


文档简介
5. 7用二元一次方程组确定一次函数表达式
学习目标
会用待定系数法解二元一次方程或一次函数,体会待定系数法的意义.
学习策略
1、 结合以前所学的二元一次方程和一次函数的知识;
2、 熟悉待定系数法的一般步骤.
学习过程
一.复习回顾:
1、如图,直线y=2x﹣4和直线y=﹣3x+1交于一点,则方程的解是( )
A. B. C. D.
2、在一次函数y=5-2x的图象上任取一点,它的坐标________方程2x+y=5(此空填“适合”或“不一定适合”).
二.新课学习:
1.自学教材P125-126,回答以下问题
(1)用做图像的方法可以直观地获得问题的结果,但是有时却难以获得;为了获得准确的结果,我们一般用 。
(2)先设出函数代表式,再根据所给的条件确定表达式中未知的系数,从而得到函数表达式的方法,叫 。
2、自学课本P126例思考下列问题:
(1)如何设函数表达式?
(2)解题的过程是怎样的?
三.尝试应用:
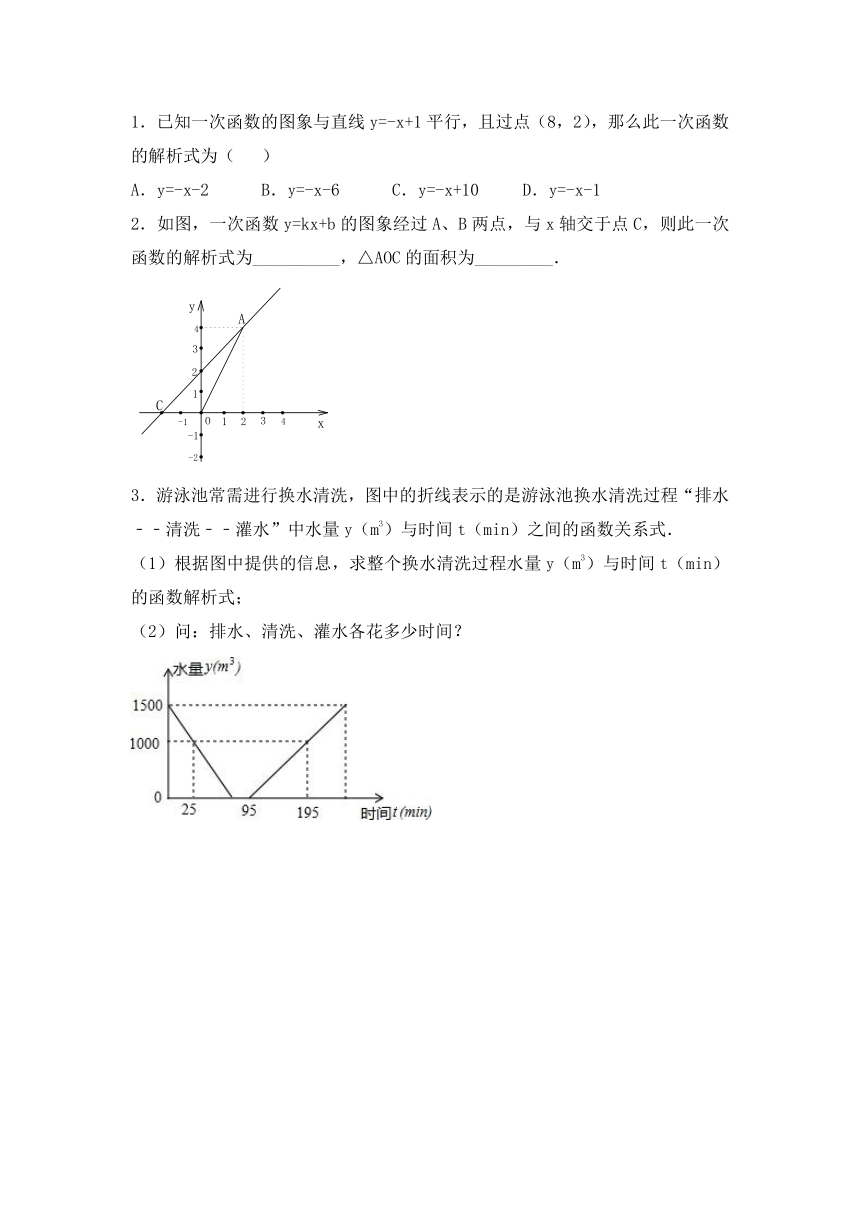
1.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为( )
A.y=-x-2 B.y=-x-6 C.y=-x+10 D.y=-x-1
2.如图,一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,则此一次函数的解析式为__________,△AOC的面积为_________.
3.游泳池常需进行换水清洗,图中的折线表示的是游泳池换水清洗过程“排水﹣﹣清洗﹣﹣灌水”中水量y(m3)与时间t(min)之间的函数关系式.
(1)根据图中提供的信息,求整个换水清洗过程水量y(m3)与时间t(min)的函数解析式;
(2)问:排水、清洗、灌水各花多少时间?
四.自主总结:
利用二元一次方程组求一次函数表达式的一般步骤:
(1)用含字母的系数设出一次函数的表式 ;
(2)将已知条件代入上述表达式中得 , 的二元一次方程组;
(3)解这个二元一次方程组得k,b,进而得到 的表达式.
五.达标测试
一、选择题
1.已知一次函数y=kx+b(k≠0)经过(2,﹣1)、(﹣3,4)两点,则它的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.直线y=kx+b的图象如图所示,则( )
A.k=-,b=-2 B.k=,b=-2 C.k=-,b=-2 D.k=,b=-2
二、填空题
3.如图,直线l是一次函数y=kx+b的图像,看图填空:
(1) b=______,k=______;
(2)当x=30时,y=_______;
(3)当y=30时,x=_______.
4.若y-1与x成正比例,且当x=-2时,y=4,那么y与x之间的函数关系式为________.
三、解答题
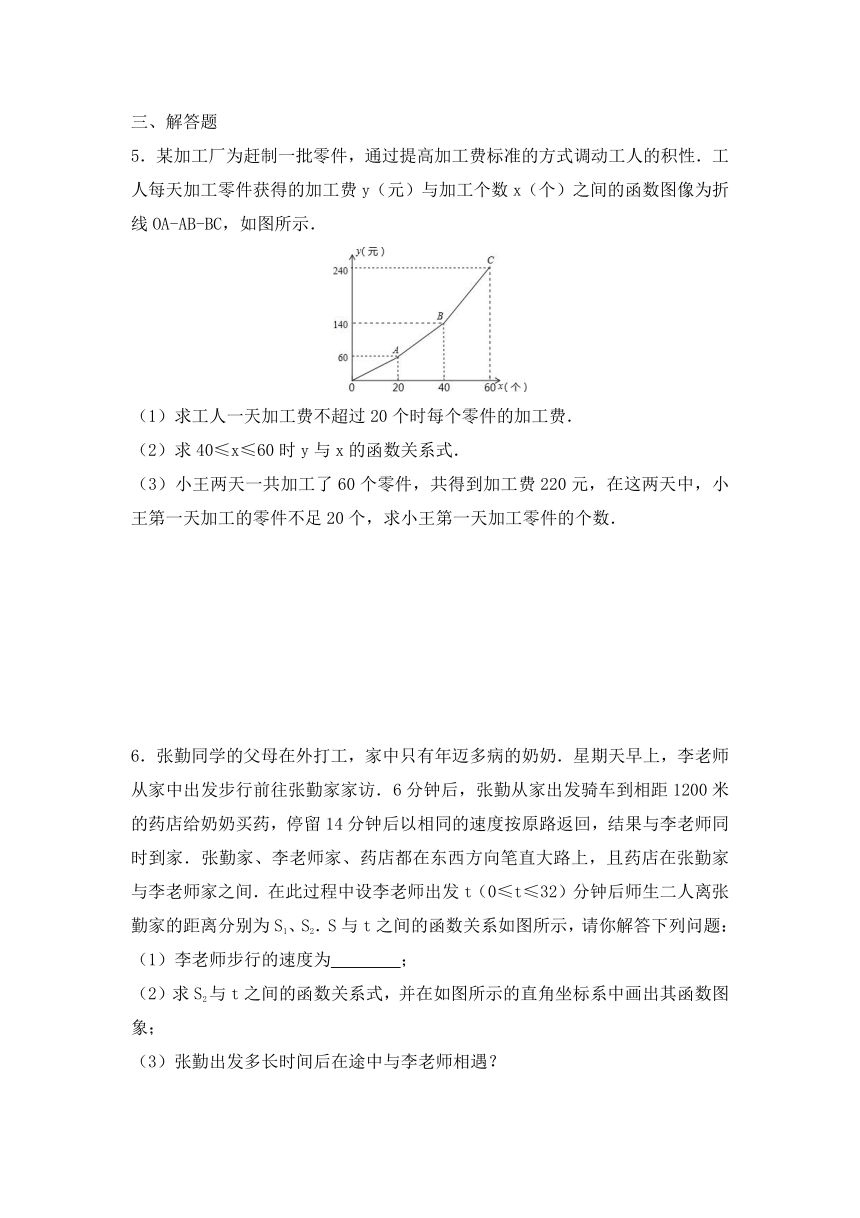
5.某加工厂为赶制一批零件,通过提高加工费标准的方式调动工人的积性.工人每天加工零件获得的加工费y(元)与加工个数x(个)之间的函数图像为折线OA-AB-BC,如图所示.
(1)求工人一天加工费不超过20个时每个零件的加工费.
(2)求40≤x≤60时y与x的函数关系式.
(3)小王两天一共加工了60个零件,共得到加工费220元,在这两天中,小王第一天加工的零件不足20个,求小王第一天加工零件的个数.
6.张勤同学的父母在外打工,家中只有年迈多病的奶奶.星期天早上,李老师从家中出发步行前往张勤家家访.6分钟后,张勤从家出发骑车到相距1200米的药店给奶奶买药,停留14分钟后以相同的速度按原路返回,结果与李老师同时到家.张勤家、李老师家、药店都在东西方向笔直大路上,且药店在张勤家与李老师家之间.在此过程中设李老师出发t(0≤t≤32)分钟后师生二人离张勤家的距离分别为S1、S2.S与t之间的函数关系如图所示,请你解答下列问题:
(1)李老师步行的速度为 ;
(2)求S2与t之间的函数关系式,并在如图所示的直角坐标系中画出其函数图象;
(3)张勤出发多长时间后在途中与李老师相遇?
7.甲、乙两个港口相距72千米,一艘轮船从甲港出发,顺流航行3小时到达乙港,休息1小时后立即返回;一艘快艇在轮船出发2小时后从乙港出发,逆流航行2小时到甲港,并立即返回(掉头时间忽略不计)。已知水流速度是2千米/时,下图表示轮船和快艇距甲港的距离y(千米)与轮船出发时间x(小时)之间的函数关系式,结合图象解答下列问题:
(顺流速度=船在静水中速度+水流速度;逆流速度=船在静水中速度-水流速度)
(1)轮船在静水中的速度是 千米/时;快艇在静水中的速度是 千米/时;
(2)求快艇返回时的解析式,写出自变量取值范围;
(3)快艇出发多长时间,轮船和快艇在返回途中相距12千米?(直接写出结果)
尝试应用答案:
1. C 2.y=x+2; 4
3.解:(1)排水阶段:设解析式为:y=kt+b,
因为图象经过(0,1500),(25,1000),
所以,解得:。所以排水阶段解析式为:y=﹣20t+1500。
清洗阶段:y=0。
灌水阶段:设解析式为:y=at+c,
因为图象经过(195,1000),(95,0),
所以,解得:。所以灌水阶段解析式为: y=10t﹣950。
(2)因为排水阶段解析式为:y=﹣20t+1500,所以令y=0,即0=﹣20t+1500,解得:t=75。
所以排水时间为75分钟。
清洗时间为:95﹣75=20(分钟),
因为根据图象可以得出游泳池蓄水量为1500 m3,
所以1500=10t﹣950,解得:t=245。故灌水所用时间为:245﹣95=150(分钟)。
达标测试答案:
一、选择题
1.C
2.B
二、填空题
3.(1)2,-1;(2)-28;(3)-28.
4.y=-x+1.
三、解答题
5.解:(1)由图象可知,当0≤x≤20时,每个零件的加工费为60÷20=3元,
即工人一天加工零件不超过20个时,每个零件的加工费为3元。
(2)当40≤x≤60时,设y与x的函数关系式为y=kx+b,
将B(40,140),C(60,240)代入,得
,解得 。
所以y与x的函数关系式为y=5x-60。
(3)设小王第一天加工零件的个数为a,则第二天加工零件的个数为(60-a),
因为 小王第一天加工的零件不足20个,小王两天一共加工了60个零件。
所以小王第二天加工的零件不足60个,超过40个。
由(2)知,第二天加工零件的加工费为5(60-a)-60。
所以5(60-a)-60=220-3a,解得,a =10。
所以小王第一天加工零件10个。
6.解:(1)50米/分。
(2)根据题意得:
当0≤t≤6时,S2=0,
当6<t≤12时,S2=200t﹣1200,
当12<t≤26时,S2=1200,
当26<t≤32时,S2=﹣200t+6400,
所以S2与t之间的函数关系式为
。
图象如图:
(3)因为图中可见,李老师从家中出发步行前往张勤家家访经过(0,1600),(32,0),
所以设S1=kx+b,则,解得。
所以S1=﹣50t+1600。
因为图中可见,张勤与李老师相遇的时间在6<t≤12,
所以由S1=S2得,200t﹣1200=﹣50t+1600,解得t=11.2。
所以张勤出发11.2秒在途中与李老师相遇。
7.解:(1)22 ; 38。
(2)点F的横坐标为:4+72÷(38+2)=5.8 。
所以F(5.8,72),E(4,0)。
设EF解析式为y=kx+b(k≠0),则
,解得。
所以y=40x-160(4≤x≤5.8)。
(3)快艇出发3小时或3.4小时两船相距12千米。
学习目标
会用待定系数法解二元一次方程或一次函数,体会待定系数法的意义.
学习策略
1、 结合以前所学的二元一次方程和一次函数的知识;
2、 熟悉待定系数法的一般步骤.
学习过程
一.复习回顾:
1、如图,直线y=2x﹣4和直线y=﹣3x+1交于一点,则方程的解是( )
A. B. C. D.
2、在一次函数y=5-2x的图象上任取一点,它的坐标________方程2x+y=5(此空填“适合”或“不一定适合”).
二.新课学习:
1.自学教材P125-126,回答以下问题
(1)用做图像的方法可以直观地获得问题的结果,但是有时却难以获得;为了获得准确的结果,我们一般用 。
(2)先设出函数代表式,再根据所给的条件确定表达式中未知的系数,从而得到函数表达式的方法,叫 。
2、自学课本P126例思考下列问题:
(1)如何设函数表达式?
(2)解题的过程是怎样的?
三.尝试应用:
1.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为( )
A.y=-x-2 B.y=-x-6 C.y=-x+10 D.y=-x-1
2.如图,一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,则此一次函数的解析式为__________,△AOC的面积为_________.
3.游泳池常需进行换水清洗,图中的折线表示的是游泳池换水清洗过程“排水﹣﹣清洗﹣﹣灌水”中水量y(m3)与时间t(min)之间的函数关系式.
(1)根据图中提供的信息,求整个换水清洗过程水量y(m3)与时间t(min)的函数解析式;
(2)问:排水、清洗、灌水各花多少时间?
四.自主总结:
利用二元一次方程组求一次函数表达式的一般步骤:
(1)用含字母的系数设出一次函数的表式 ;
(2)将已知条件代入上述表达式中得 , 的二元一次方程组;
(3)解这个二元一次方程组得k,b,进而得到 的表达式.
五.达标测试
一、选择题
1.已知一次函数y=kx+b(k≠0)经过(2,﹣1)、(﹣3,4)两点,则它的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.直线y=kx+b的图象如图所示,则( )
A.k=-,b=-2 B.k=,b=-2 C.k=-,b=-2 D.k=,b=-2
二、填空题
3.如图,直线l是一次函数y=kx+b的图像,看图填空:
(1) b=______,k=______;
(2)当x=30时,y=_______;
(3)当y=30时,x=_______.
4.若y-1与x成正比例,且当x=-2时,y=4,那么y与x之间的函数关系式为________.
三、解答题
5.某加工厂为赶制一批零件,通过提高加工费标准的方式调动工人的积性.工人每天加工零件获得的加工费y(元)与加工个数x(个)之间的函数图像为折线OA-AB-BC,如图所示.
(1)求工人一天加工费不超过20个时每个零件的加工费.
(2)求40≤x≤60时y与x的函数关系式.
(3)小王两天一共加工了60个零件,共得到加工费220元,在这两天中,小王第一天加工的零件不足20个,求小王第一天加工零件的个数.
6.张勤同学的父母在外打工,家中只有年迈多病的奶奶.星期天早上,李老师从家中出发步行前往张勤家家访.6分钟后,张勤从家出发骑车到相距1200米的药店给奶奶买药,停留14分钟后以相同的速度按原路返回,结果与李老师同时到家.张勤家、李老师家、药店都在东西方向笔直大路上,且药店在张勤家与李老师家之间.在此过程中设李老师出发t(0≤t≤32)分钟后师生二人离张勤家的距离分别为S1、S2.S与t之间的函数关系如图所示,请你解答下列问题:
(1)李老师步行的速度为 ;
(2)求S2与t之间的函数关系式,并在如图所示的直角坐标系中画出其函数图象;
(3)张勤出发多长时间后在途中与李老师相遇?
7.甲、乙两个港口相距72千米,一艘轮船从甲港出发,顺流航行3小时到达乙港,休息1小时后立即返回;一艘快艇在轮船出发2小时后从乙港出发,逆流航行2小时到甲港,并立即返回(掉头时间忽略不计)。已知水流速度是2千米/时,下图表示轮船和快艇距甲港的距离y(千米)与轮船出发时间x(小时)之间的函数关系式,结合图象解答下列问题:
(顺流速度=船在静水中速度+水流速度;逆流速度=船在静水中速度-水流速度)
(1)轮船在静水中的速度是 千米/时;快艇在静水中的速度是 千米/时;
(2)求快艇返回时的解析式,写出自变量取值范围;
(3)快艇出发多长时间,轮船和快艇在返回途中相距12千米?(直接写出结果)
尝试应用答案:
1. C 2.y=x+2; 4
3.解:(1)排水阶段:设解析式为:y=kt+b,
因为图象经过(0,1500),(25,1000),
所以,解得:。所以排水阶段解析式为:y=﹣20t+1500。
清洗阶段:y=0。
灌水阶段:设解析式为:y=at+c,
因为图象经过(195,1000),(95,0),
所以,解得:。所以灌水阶段解析式为: y=10t﹣950。
(2)因为排水阶段解析式为:y=﹣20t+1500,所以令y=0,即0=﹣20t+1500,解得:t=75。
所以排水时间为75分钟。
清洗时间为:95﹣75=20(分钟),
因为根据图象可以得出游泳池蓄水量为1500 m3,
所以1500=10t﹣950,解得:t=245。故灌水所用时间为:245﹣95=150(分钟)。
达标测试答案:
一、选择题
1.C
2.B
二、填空题
3.(1)2,-1;(2)-28;(3)-28.
4.y=-x+1.
三、解答题
5.解:(1)由图象可知,当0≤x≤20时,每个零件的加工费为60÷20=3元,
即工人一天加工零件不超过20个时,每个零件的加工费为3元。
(2)当40≤x≤60时,设y与x的函数关系式为y=kx+b,
将B(40,140),C(60,240)代入,得
,解得 。
所以y与x的函数关系式为y=5x-60。
(3)设小王第一天加工零件的个数为a,则第二天加工零件的个数为(60-a),
因为 小王第一天加工的零件不足20个,小王两天一共加工了60个零件。
所以小王第二天加工的零件不足60个,超过40个。
由(2)知,第二天加工零件的加工费为5(60-a)-60。
所以5(60-a)-60=220-3a,解得,a =10。
所以小王第一天加工零件10个。
6.解:(1)50米/分。
(2)根据题意得:
当0≤t≤6时,S2=0,
当6<t≤12时,S2=200t﹣1200,
当12<t≤26时,S2=1200,
当26<t≤32时,S2=﹣200t+6400,
所以S2与t之间的函数关系式为
。
图象如图:
(3)因为图中可见,李老师从家中出发步行前往张勤家家访经过(0,1600),(32,0),
所以设S1=kx+b,则,解得。
所以S1=﹣50t+1600。
因为图中可见,张勤与李老师相遇的时间在6<t≤12,
所以由S1=S2得,200t﹣1200=﹣50t+1600,解得t=11.2。
所以张勤出发11.2秒在途中与李老师相遇。
7.解:(1)22 ; 38。
(2)点F的横坐标为:4+72÷(38+2)=5.8 。
所以F(5.8,72),E(4,0)。
设EF解析式为y=kx+b(k≠0),则
,解得。
所以y=40x-160(4≤x≤5.8)。
(3)快艇出发3小时或3.4小时两船相距12千米。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
