人教版数学八年级上册 14.1.4 整式的乘法 第3课时 同底数幂的除法 课件(共18张PPT)
文档属性
| 名称 | 人教版数学八年级上册 14.1.4 整式的乘法 第3课时 同底数幂的除法 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第3课时 同底数幂的除法
14.1.4 整式的乘法
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
一个数码相机的相机照片文件大小是210Kb,一个存储量为220Kb的U盘能存储多少张这样数码照片呢?你会计算吗?
新课导入
讲授新知
贰
x4
102
210
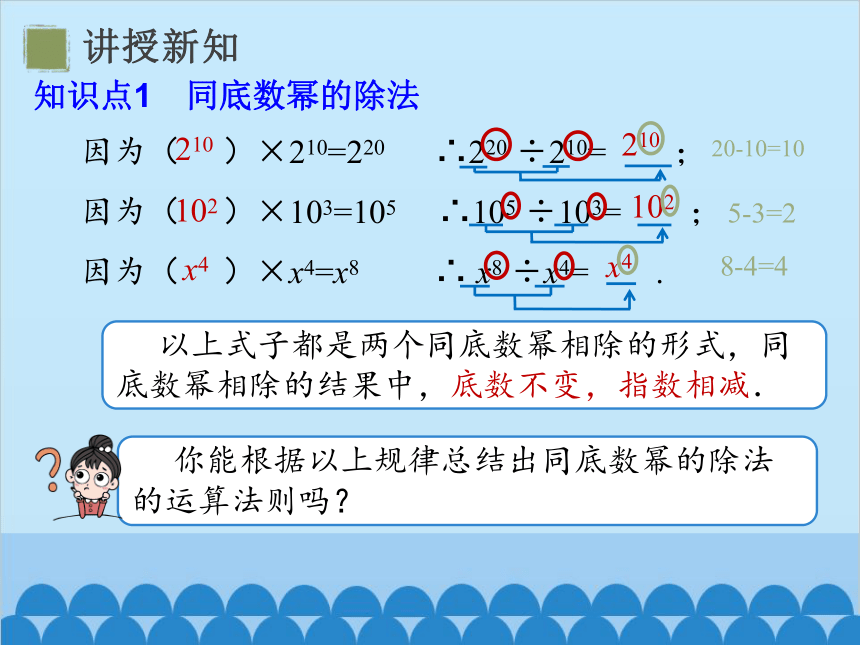
因为( )×210=220 ∴220 ÷210= ;
因为( )×103=105 ∴105 ÷103= ;
因为( )×x4=x8 ∴ x8 ÷x4= .
20-10=10
5-3=2
8-4=4
你能根据以上规律总结出同底数幂的除法的运算法则吗?
以上式子都是两个同底数幂相除的形式,同底数幂相除的结果中,底数不变,指数相减.
210
102
x4
知识点1 同底数幂的除法
讲授新知
一般地,我们有
am ÷an=am-n (a ≠0,m,n都是正整数,且m>n)
即 同底数幂相除,底数不变,指数相减.
同底数幂的除法
想一想:am÷am= (a≠0)
答:am÷am=1,根据同底数幂的除法法则可得am÷am=a0.
规定
a0 =1(a ≠0)
这就是说,任何不等于0的数的0次幂都等于1.
讲授新知
同底数幂的除法的示例:
底数不变
指数相减
(1) 底数可以是单项式,也可以是多项式,但不可以是 0;
(2) 同底数幂相除,底数不变,指数是相减而不是相除.
温馨提示
讲授新知
例1 计算:
(1)x8÷x2; (2)(ab)5÷(ab)2.
解:(1)x8÷x2
=x8-2
=x6;
(2)(ab)5÷(ab)2
=(ab)5-2
=(ab)3
=a3b3
范例应用
零指数幂的示例:
底数是-2
指数为0
结果为1
底数是100
指数为0
结果为1
知识点2 零指数幂
性质:任何不等于0的数的零次幂都等于1.
符号表示:a0=1(a≠0).
(1) 零指数幂中的底数可以是单项式,也可以是多项式,但不可以是0;
(2) 因为 a=0 时,a0 无意义,所以 a0 有意义的条件是 a≠0,常据此确定底数中所含字母的取值范围.
讲授新知
例2 已知3x-2=1,求x的值.
解:因为30=1,
所以x-2=0,
所以x=2.
范例应用
当堂训练
叁
当堂训练
1.计算(a3)2÷a2的结果是( )
A. a3 B. a4 C. a7 D. a8
2.计算:(-a)3÷a 结果正确的是( )
A. a2 B. -a2 C. -a3 D. -a4
3.若 (2x-6)0=1,则 x 的取值范围是( )
A. x≠0 B. x≠3 C. x=3 D. x=0
4.计算16m÷4n÷2等于( )
A.2m-n-1 B.22m-n-1 C.23m-2n-1 D.24m-2n-1
5.计算:(π-1)0+|-2|=_____.
B
B
B
D
3
解:(1) (-xy)13÷(-xy)8=(-xy)13-8=(-xy)5=-x5y5 ;
(2) a2m+4÷am-2=a2m+4-m+2=am+6 ;
(3) (x-2y)3÷(2y-x)2
= (x-2y)3÷[-(x-2y)]2
= (x-2y)3÷ (x-2y)2
= x-2y .
6.计算下列式子:
(-xy)13÷(-xy)8 ; (2) a2m+4÷am-2 ;
(3) (x-2y)3÷(2y-x)2 .
当堂训练
课堂小结
肆
性质:同底数幂相除,
底数不变,指数相减
同底数幂的除法
am÷an=am-n(a≠0,m,n都是正整数,并且m>n).
零指数幂
任何不等于0的数的0次幂都等于1
a0=1(a≠0)
课堂小结
课后作业
基础题:1.课后练习 P104第 1题。
提高题:2.请学有余力的同学做同步训练对应的本节的题.
谢
谢
第3课时 同底数幂的除法
14.1.4 整式的乘法
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
一个数码相机的相机照片文件大小是210Kb,一个存储量为220Kb的U盘能存储多少张这样数码照片呢?你会计算吗?
新课导入
讲授新知
贰
x4
102
210
因为( )×210=220 ∴220 ÷210= ;
因为( )×103=105 ∴105 ÷103= ;
因为( )×x4=x8 ∴ x8 ÷x4= .
20-10=10
5-3=2
8-4=4
你能根据以上规律总结出同底数幂的除法的运算法则吗?
以上式子都是两个同底数幂相除的形式,同底数幂相除的结果中,底数不变,指数相减.
210
102
x4
知识点1 同底数幂的除法
讲授新知
一般地,我们有
am ÷an=am-n (a ≠0,m,n都是正整数,且m>n)
即 同底数幂相除,底数不变,指数相减.
同底数幂的除法
想一想:am÷am= (a≠0)
答:am÷am=1,根据同底数幂的除法法则可得am÷am=a0.
规定
a0 =1(a ≠0)
这就是说,任何不等于0的数的0次幂都等于1.
讲授新知
同底数幂的除法的示例:
底数不变
指数相减
(1) 底数可以是单项式,也可以是多项式,但不可以是 0;
(2) 同底数幂相除,底数不变,指数是相减而不是相除.
温馨提示
讲授新知
例1 计算:
(1)x8÷x2; (2)(ab)5÷(ab)2.
解:(1)x8÷x2
=x8-2
=x6;
(2)(ab)5÷(ab)2
=(ab)5-2
=(ab)3
=a3b3
范例应用
零指数幂的示例:
底数是-2
指数为0
结果为1
底数是100
指数为0
结果为1
知识点2 零指数幂
性质:任何不等于0的数的零次幂都等于1.
符号表示:a0=1(a≠0).
(1) 零指数幂中的底数可以是单项式,也可以是多项式,但不可以是0;
(2) 因为 a=0 时,a0 无意义,所以 a0 有意义的条件是 a≠0,常据此确定底数中所含字母的取值范围.
讲授新知
例2 已知3x-2=1,求x的值.
解:因为30=1,
所以x-2=0,
所以x=2.
范例应用
当堂训练
叁
当堂训练
1.计算(a3)2÷a2的结果是( )
A. a3 B. a4 C. a7 D. a8
2.计算:(-a)3÷a 结果正确的是( )
A. a2 B. -a2 C. -a3 D. -a4
3.若 (2x-6)0=1,则 x 的取值范围是( )
A. x≠0 B. x≠3 C. x=3 D. x=0
4.计算16m÷4n÷2等于( )
A.2m-n-1 B.22m-n-1 C.23m-2n-1 D.24m-2n-1
5.计算:(π-1)0+|-2|=_____.
B
B
B
D
3
解:(1) (-xy)13÷(-xy)8=(-xy)13-8=(-xy)5=-x5y5 ;
(2) a2m+4÷am-2=a2m+4-m+2=am+6 ;
(3) (x-2y)3÷(2y-x)2
= (x-2y)3÷[-(x-2y)]2
= (x-2y)3÷ (x-2y)2
= x-2y .
6.计算下列式子:
(-xy)13÷(-xy)8 ; (2) a2m+4÷am-2 ;
(3) (x-2y)3÷(2y-x)2 .
当堂训练
课堂小结
肆
性质:同底数幂相除,
底数不变,指数相减
同底数幂的除法
am÷an=am-n(a≠0,m,n都是正整数,并且m>n).
零指数幂
任何不等于0的数的0次幂都等于1
a0=1(a≠0)
课堂小结
课后作业
基础题:1.课后练习 P104第 1题。
提高题:2.请学有余力的同学做同步训练对应的本节的题.
谢
谢
