2022-2023学年人教版数学九年级上册22.1 二次函数的图像和性质 同步练习(含答案)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册22.1 二次函数的图像和性质 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 55.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 07:01:05 | ||
图片预览

文档简介
22.1 二次函数的图像和性质同步练习 2022-2023学年人教版数学九年级上册
一、单选题
1.已知二次函数,则此二次函数( )
A.有最大值1 B.有最小值1 C.有最大值-3 D.有最小值-3
2.由二次函数y=6(x﹣2)2+1,可知( )
A.图象的开口向下 B.图象的对称轴为直线x=
C.函数的最大值为1 D.当x>2时,y随x的增大而增大
3.已知二次函数 在 时有最小值 ,则t的值是( )
A.0或2 B. 或 C.2或 D.0或
4.若点,在抛物线上,则的值为( )
A.2 B.1 C.0 D.-1
5.已知抛物线y=ax2﹣2x+1与x轴没有交点,那么a的取值范围是( )
A.a>1 B.a<1 C.a≥1 D.a≤1
6.关于二次函数的图象,下列结论正确的是( )
A.开口向下
B.对称轴是直线
C.顶点纵坐标是-3
D.当时,函数值随值的增大而增大
7.已知某二次函数的图象如图所示,则这个二次函数的解析式为( )
A. B.
C. D.
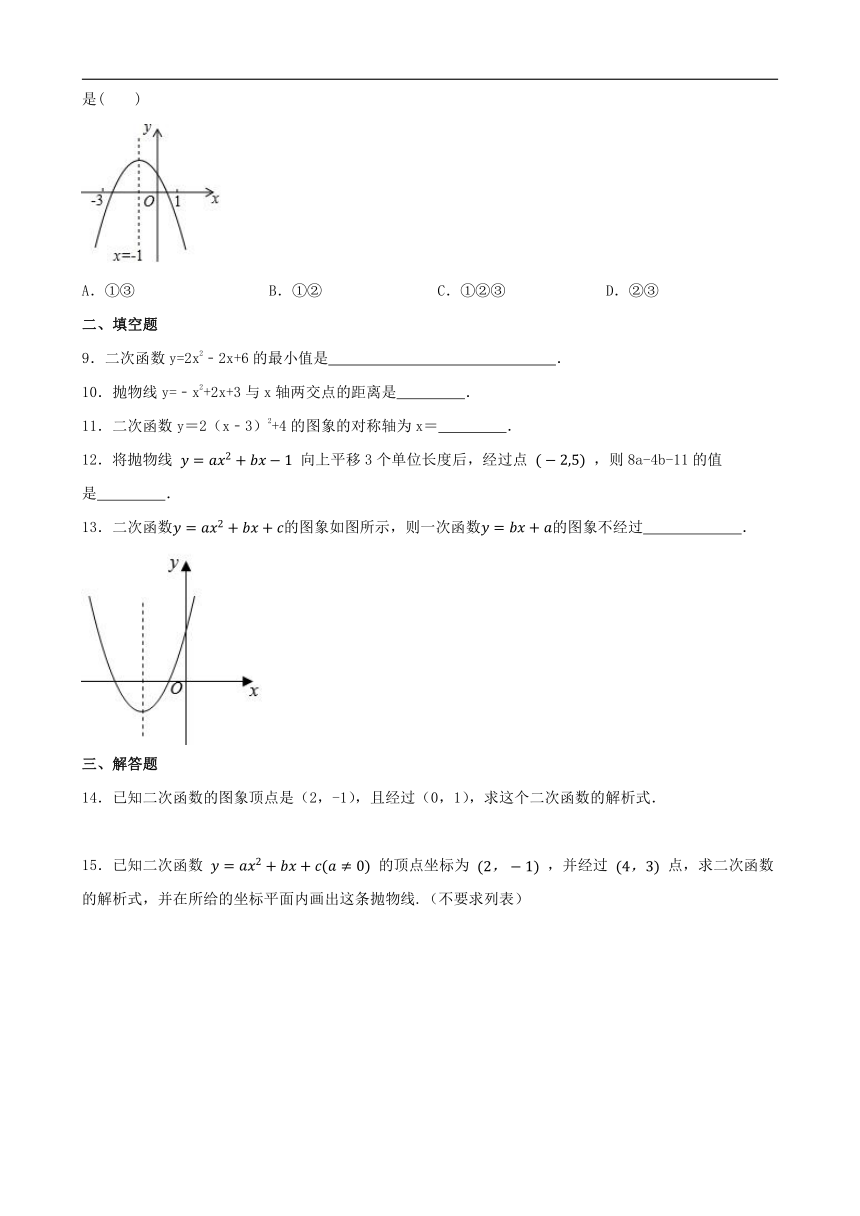
8.二次函数y=ax2+bx+c的图象如图所示、则下列结论:①abc>0;②a﹣5b+9c>0;③3a+c<0,正确的是( )
A.①③ B.①② C.①②③ D.②③
二、填空题
9.二次函数y=2x2﹣2x+6的最小值是 .
10.抛物线y=﹣x2+2x+3与x轴两交点的距离是 .
11.二次函数y=2(x﹣3)2+4的图象的对称轴为x= .
12.将抛物线 向上平移3个单位长度后,经过点 ,则8a-4b-11的值是 .
13.二次函数的图象如图所示,则一次函数的图象不经过 .
三、解答题
14.已知二次函数的图象顶点是(2,-1),且经过(0,1),求这个二次函数的解析式.
15.已知二次函数 的顶点坐标为 ,并经过 点,求二次函数的解析式,并在所给的坐标平面内画出这条抛物线.(不要求列表)
16.在直角坐标平面内,点 O为坐标原点,二次函数 y=x2+(k﹣5)x﹣(k+4)的图象交 x轴于点A(x1,0)、B(x2,0),且(x1+1)(x2+1)=﹣8.求二次函数解析式.
17.如图A(﹣4,0),C(0,3),将线段CA以点C为旋转中心旋转,所得的对应线段记为CA',当点A'落在y轴上时,写出A'的坐标,并求出以A'为顶点,经过A(﹣4,0)的抛物线的解析式.
18.已知y是关于x的二次函数,x与y的部分对应值如下表所示:
x的值 ﹣2 0 2 4
y的值 4 ﹣2 0 m
(1)求y关于x的二次函数解析式;
(2)求m的值.
19.张师傅准备用长为8cm的铜丝剪成两段,以围成两个正方形的线圈,设剪成的两段铜丝中的一段的长为xcm,围成的两个正方形的面积之和为Scm2.
(1)求S与x的函数关系式,并写出自变量的取值范围;
(2)当x取何值时,S取得最小值,并求出这个最小值.
参考答案
1.A
2.D
3.D
4.C
5.D
6.B
7.A
8.C
9.
10.4
11.3
12.-5
13.第四象限
14.解:设二次函数的解析式是y=a(x-2)2-1,
把(0,1)代入,得4a=2,即a=
∴该二次函数的解析式是y=(x-2)2-1.
15.解:依题意设二次函数的解析式为 ,
将 , 代入,得 ,
解得 ,
∴二次函数的解析式为 ;
如图所示.
16.解:由题意得:x1,x2为方程x2+(k﹣5)x﹣(k+4)=0的解,
∴x1+x2=﹣(k﹣5)=5﹣k,x1x2=﹣(k+4)=﹣k﹣4,
∵(x1+1)(x2+1)﹣8,即x1x2+(x1+x2)+1=﹣8,
∴﹣k﹣4+5﹣k+1=﹣8,
解得:k=5,
则y=x2﹣9
17.解:∵A(﹣4,0),C(0,3),
∴AC= =5.①当将线段CA以点C为旋转中心,顺时针旋转时,A′(0,8).
设该函数解析式为y=ax2+8.
把A(﹣4,0)代入得到:0=16a+8,
解得a=﹣ .
故该函数解析式为:y=﹣ x2+8.②当将线段CA以点C为旋转中心,逆时针旋转时,A′(0,2).
设该函数解析式为y=ax2﹣2.
把A(﹣4,0)代入得到:0=16a﹣2,
解得a= .
故该函数解析式为:y= x2+2.
综上所述,该二次函数解析式为:y=﹣ x2+8或y= x2+2
18.(1)解:设此二次函数解析式为y=ax2+bx+c,由题意列出方程组 ,
解得a=1,b=﹣1,c=﹣2,
所以二次函数解析式为y=x2﹣x﹣2
(2)解:将x=4代入解析式得m=10
19.(1)解:设一段铁丝的长度为x,另一段为(8﹣x),则边长分别为 x, (8﹣x),
则S= x2+ (8﹣x)(8﹣x)= x2﹣x+4;自变量的取值范围:0<x<8
(2)解:S= (x﹣4)2+2,
所以当x=4cm时,S最小,最小为2cm2
一、单选题
1.已知二次函数,则此二次函数( )
A.有最大值1 B.有最小值1 C.有最大值-3 D.有最小值-3
2.由二次函数y=6(x﹣2)2+1,可知( )
A.图象的开口向下 B.图象的对称轴为直线x=
C.函数的最大值为1 D.当x>2时,y随x的增大而增大
3.已知二次函数 在 时有最小值 ,则t的值是( )
A.0或2 B. 或 C.2或 D.0或
4.若点,在抛物线上,则的值为( )
A.2 B.1 C.0 D.-1
5.已知抛物线y=ax2﹣2x+1与x轴没有交点,那么a的取值范围是( )
A.a>1 B.a<1 C.a≥1 D.a≤1
6.关于二次函数的图象,下列结论正确的是( )
A.开口向下
B.对称轴是直线
C.顶点纵坐标是-3
D.当时,函数值随值的增大而增大
7.已知某二次函数的图象如图所示,则这个二次函数的解析式为( )
A. B.
C. D.
8.二次函数y=ax2+bx+c的图象如图所示、则下列结论:①abc>0;②a﹣5b+9c>0;③3a+c<0,正确的是( )
A.①③ B.①② C.①②③ D.②③
二、填空题
9.二次函数y=2x2﹣2x+6的最小值是 .
10.抛物线y=﹣x2+2x+3与x轴两交点的距离是 .
11.二次函数y=2(x﹣3)2+4的图象的对称轴为x= .
12.将抛物线 向上平移3个单位长度后,经过点 ,则8a-4b-11的值是 .
13.二次函数的图象如图所示,则一次函数的图象不经过 .
三、解答题
14.已知二次函数的图象顶点是(2,-1),且经过(0,1),求这个二次函数的解析式.
15.已知二次函数 的顶点坐标为 ,并经过 点,求二次函数的解析式,并在所给的坐标平面内画出这条抛物线.(不要求列表)
16.在直角坐标平面内,点 O为坐标原点,二次函数 y=x2+(k﹣5)x﹣(k+4)的图象交 x轴于点A(x1,0)、B(x2,0),且(x1+1)(x2+1)=﹣8.求二次函数解析式.
17.如图A(﹣4,0),C(0,3),将线段CA以点C为旋转中心旋转,所得的对应线段记为CA',当点A'落在y轴上时,写出A'的坐标,并求出以A'为顶点,经过A(﹣4,0)的抛物线的解析式.
18.已知y是关于x的二次函数,x与y的部分对应值如下表所示:
x的值 ﹣2 0 2 4
y的值 4 ﹣2 0 m
(1)求y关于x的二次函数解析式;
(2)求m的值.
19.张师傅准备用长为8cm的铜丝剪成两段,以围成两个正方形的线圈,设剪成的两段铜丝中的一段的长为xcm,围成的两个正方形的面积之和为Scm2.
(1)求S与x的函数关系式,并写出自变量的取值范围;
(2)当x取何值时,S取得最小值,并求出这个最小值.
参考答案
1.A
2.D
3.D
4.C
5.D
6.B
7.A
8.C
9.
10.4
11.3
12.-5
13.第四象限
14.解:设二次函数的解析式是y=a(x-2)2-1,
把(0,1)代入,得4a=2,即a=
∴该二次函数的解析式是y=(x-2)2-1.
15.解:依题意设二次函数的解析式为 ,
将 , 代入,得 ,
解得 ,
∴二次函数的解析式为 ;
如图所示.
16.解:由题意得:x1,x2为方程x2+(k﹣5)x﹣(k+4)=0的解,
∴x1+x2=﹣(k﹣5)=5﹣k,x1x2=﹣(k+4)=﹣k﹣4,
∵(x1+1)(x2+1)﹣8,即x1x2+(x1+x2)+1=﹣8,
∴﹣k﹣4+5﹣k+1=﹣8,
解得:k=5,
则y=x2﹣9
17.解:∵A(﹣4,0),C(0,3),
∴AC= =5.①当将线段CA以点C为旋转中心,顺时针旋转时,A′(0,8).
设该函数解析式为y=ax2+8.
把A(﹣4,0)代入得到:0=16a+8,
解得a=﹣ .
故该函数解析式为:y=﹣ x2+8.②当将线段CA以点C为旋转中心,逆时针旋转时,A′(0,2).
设该函数解析式为y=ax2﹣2.
把A(﹣4,0)代入得到:0=16a﹣2,
解得a= .
故该函数解析式为:y= x2+2.
综上所述,该二次函数解析式为:y=﹣ x2+8或y= x2+2
18.(1)解:设此二次函数解析式为y=ax2+bx+c,由题意列出方程组 ,
解得a=1,b=﹣1,c=﹣2,
所以二次函数解析式为y=x2﹣x﹣2
(2)解:将x=4代入解析式得m=10
19.(1)解:设一段铁丝的长度为x,另一段为(8﹣x),则边长分别为 x, (8﹣x),
则S= x2+ (8﹣x)(8﹣x)= x2﹣x+4;自变量的取值范围:0<x<8
(2)解:S= (x﹣4)2+2,
所以当x=4cm时,S最小,最小为2cm2
同课章节目录
