多边形的内角和[下学期]
文档属性
| 名称 | 多边形的内角和[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 735.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-22 00:00:00 | ||
图片预览




文档简介
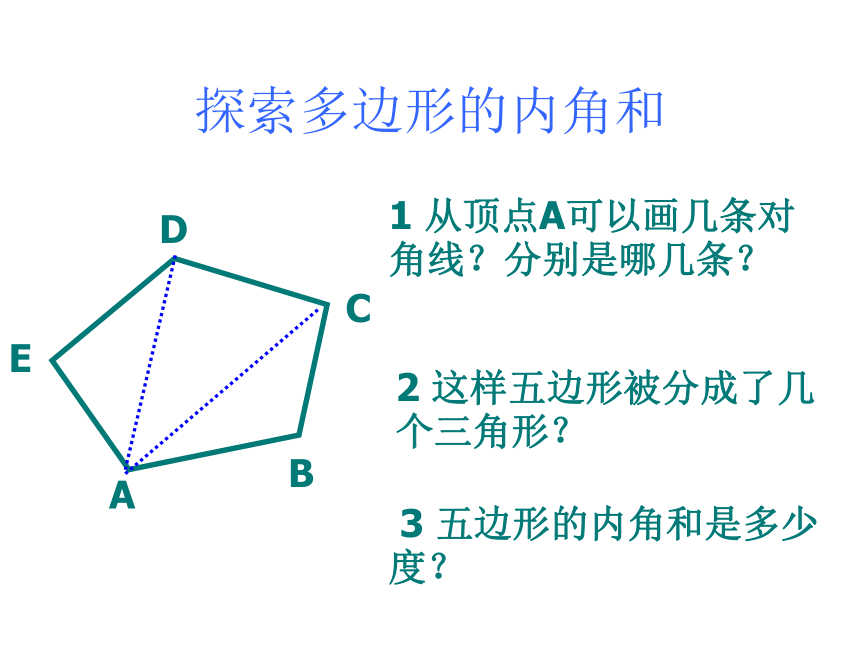
课件19张PPT。7.3.2多边形的内角和如皋初级中学 初一数学备课组 探索多边形的内角和1 从顶点A可以画几条对角线?分别是哪几条?2 这样五边形被分成了几个三角形? 3 五边形的内角和是多少度?
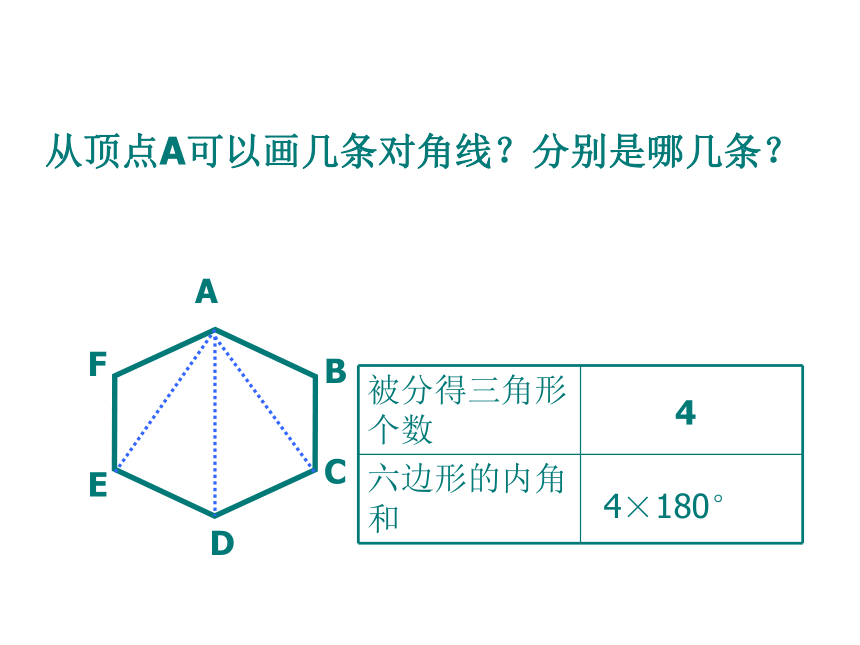
ABCDEF44×180°从顶点A可以画几条对角线?分别是哪几条?探索多边形的内角和这种探索方法你掌握了吗?请完成下表345n-25× 180°(n-2)×180°3× 180°
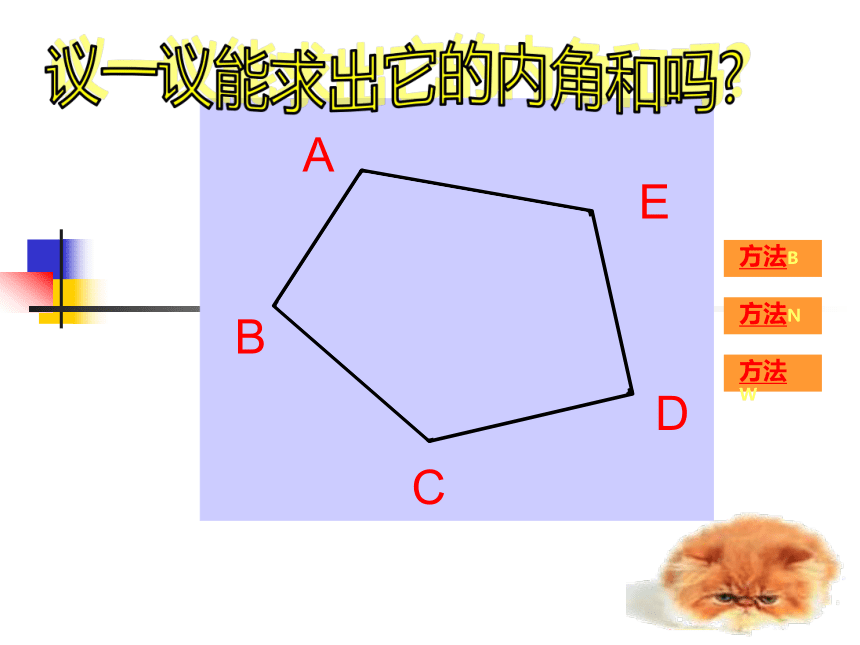
4× 180°议一议能求出它的内角和吗?ABCDE虚线计算ABCDE180? ? 4- 180 ?= 540 ?虚线计算ABCDE180? ? 5- 360 ?= 540 ?虚线计算ABCDE180? ? 4- 180 ?= 540 ?求下列图形中x的值:做一做练习:1.八边形内角和的度数等于 . (n-2) ×180°= (8-2) × 180°=1080° 2.一个多边形的内角和是1800°, 则它是 边形. (n-2) × 180°= 1800°
n=12 3.已知一个多边形每个内角都等于 108° ,求这个多边形的边数?解:设这个多边形的边数为n,根据题意得:
(n-2) ×180=108n
解得:n=5 答:这个多边形是五边形。例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系? A解:如图,四边形ABCD中,
∠A+∠C=180°例2 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少? 我们也可以象以下这种,理解为什么多边形的外角和等于360°. 结论:任意多边形的外角 和
等于360o 。 类比前边的做法,你能归纳出n 边形的
外角和是多少吗? ∵ n边形的每一个外角与它相邻的内角的和是_____
∴ n边形的内角和加外角和等于 ________
∵ n 边形的内角和等于 ___________A1A2A3AnA4180o ,(n-2) ? 180o ,∴ n 边形的外角和等于n ? 180o – (n-2) ? 180o =360o。n?180o,
解:设多边形的边数为n,因为它的外角和等于360o
所以 72o · n=360o
解得 n=5
2、已知一个多边形,它的内角和等于外角和的2倍, 求这个多边形的边数。
练习2 1、一个多边形的每一个外角都等于72o,这个多边形是 几边形?它的内角和是多少度?1、我们学会了许多解决数学问题的思想方法,如将多边形问题转化为三角形问题,以及类比方法,化未知为已知的思想方法等。
2、通过探索多边形的内角和公式,我们尝试了从不同的角度寻求解决问题的方法,并且能有效地解决问题。
3、我们还学会了运用多边形内角和公式进行相关计算。本节课收获
ABCDEF44×180°从顶点A可以画几条对角线?分别是哪几条?探索多边形的内角和这种探索方法你掌握了吗?请完成下表345n-25× 180°(n-2)×180°3× 180°
4× 180°议一议能求出它的内角和吗?ABCDE虚线计算ABCDE180? ? 4- 180 ?= 540 ?虚线计算ABCDE180? ? 5- 360 ?= 540 ?虚线计算ABCDE180? ? 4- 180 ?= 540 ?求下列图形中x的值:做一做练习:1.八边形内角和的度数等于 . (n-2) ×180°= (8-2) × 180°=1080° 2.一个多边形的内角和是1800°, 则它是 边形. (n-2) × 180°= 1800°
n=12 3.已知一个多边形每个内角都等于 108° ,求这个多边形的边数?解:设这个多边形的边数为n,根据题意得:
(n-2) ×180=108n
解得:n=5 答:这个多边形是五边形。例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系? A解:如图,四边形ABCD中,
∠A+∠C=180°例2 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少? 我们也可以象以下这种,理解为什么多边形的外角和等于360°. 结论:任意多边形的外角 和
等于360o 。 类比前边的做法,你能归纳出n 边形的
外角和是多少吗? ∵ n边形的每一个外角与它相邻的内角的和是_____
∴ n边形的内角和加外角和等于 ________
∵ n 边形的内角和等于 ___________A1A2A3AnA4180o ,(n-2) ? 180o ,∴ n 边形的外角和等于n ? 180o – (n-2) ? 180o =360o。n?180o,
解:设多边形的边数为n,因为它的外角和等于360o
所以 72o · n=360o
解得 n=5
2、已知一个多边形,它的内角和等于外角和的2倍, 求这个多边形的边数。
练习2 1、一个多边形的每一个外角都等于72o,这个多边形是 几边形?它的内角和是多少度?1、我们学会了许多解决数学问题的思想方法,如将多边形问题转化为三角形问题,以及类比方法,化未知为已知的思想方法等。
2、通过探索多边形的内角和公式,我们尝试了从不同的角度寻求解决问题的方法,并且能有效地解决问题。
3、我们还学会了运用多边形内角和公式进行相关计算。本节课收获
