24.4弧长及扇形的面积 同步练习(含答案) 2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 24.4弧长及扇形的面积 同步练习(含答案) 2023-2024学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 653.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 12:29:40 | ||
图片预览


文档简介
24.4弧长及扇形的面积 同步练习
一、单选题
1.如图,两个大小一样的传送轮连接着一条传送带,则这条传送带的长为( )
A. B. C. D.
2.若圆锥的底面半径为3,母线长为5,则这个圆锥的侧面积为( )
A.15 B.12π C.15π D.30π
3.如图,在中,,,则图中阴影部分的面积为( )
A. B. C. D.
4.如图,是等腰直角三角形,,,把绕点A沿顺时针方向旋转45°后得到,则线段在上述旋转过程中所扫过的部分(阴影部分)的面积是( )
A. B. C. D.
5.数学课上,老师将如图边长为1的正方形铁丝框变形成以A为圆心,为半径的扇形(铁丝的粗细忽略不计),则所得扇形DAB的面积是( )
A.1 B.1.5 C.2 D.
6.如图,将腰长为的等腰绕点旋转至的位置,使、、三点在同一条直线上,则点经过的最短路线长是( )
A. B. C. D.
7.一个扇形的弧长是,半径是4,则该扇形的圆心角的度数是( )
A. B. C. D.
8.一个扇形的面积为.弧长为.那么这个扇形的半径是( )
A.20 B.24 C.26 D.32
二、填空题
9.圆锥的侧面积为,母线长为5.则这个圆锥的底面半径为 .
10.已知圆锥底面积是30平方厘米,高是15厘米,则这个圆锥的体积为 立方厘米.
11.一个圆锥的底面半径为,侧面展开图是半圆,则该圆锥的高是 .
12.已知圆锥底面圆的周长为,圆锥的母线为3,则该圆锥的侧面展开图的圆心角为 .
13.如图,圆锥的底面半径为,母线长为,一只蜘蛛从底面圆周上一点出发沿圆锥的侧面爬行一周后回到点处的最短路程是 .
三、解答题
14.如图,圆锥的底面半径,高,求该圆锥的侧面积.
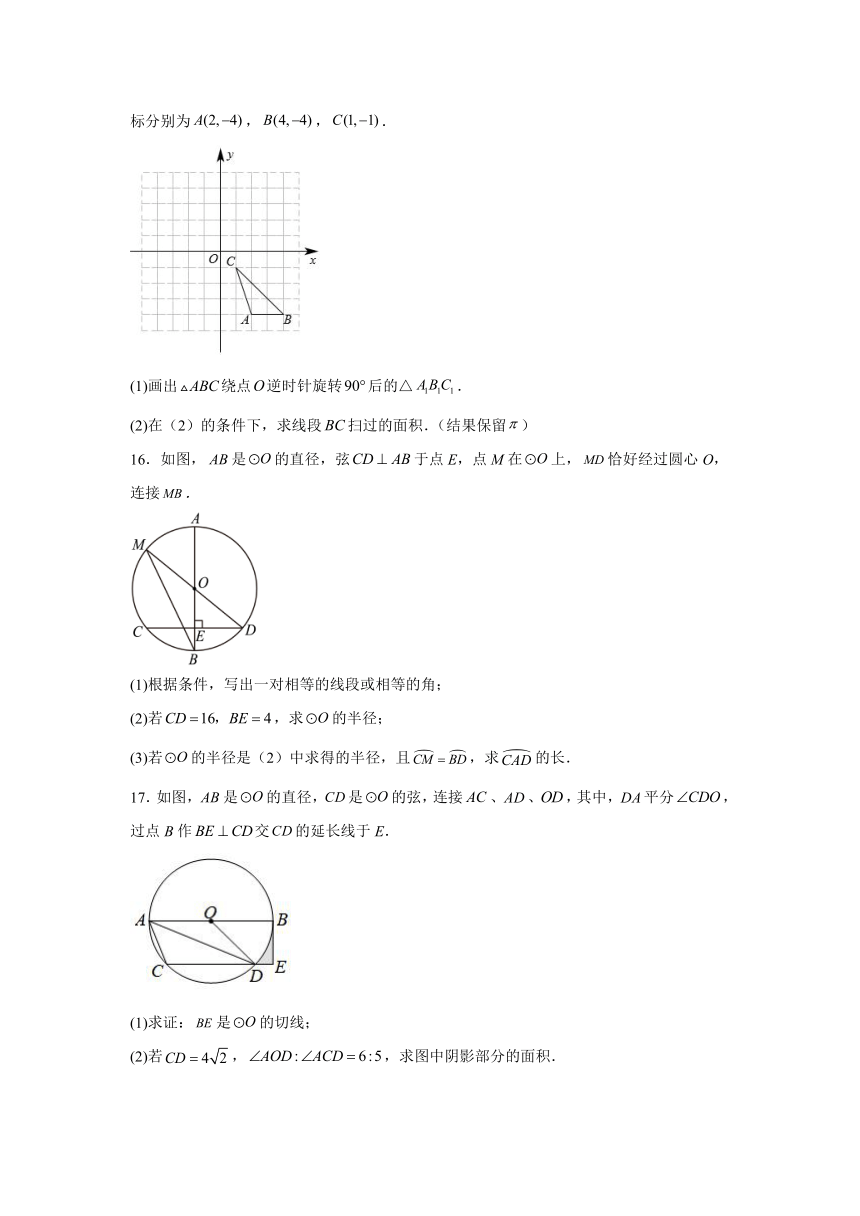
15.如图,在正方形网格中,每个小正方形的边长都是1个单位长度,的三个顶点坐标分别为,,.
(1)画出绕点逆时针旋转后的△.
(2)在(2)的条件下,求线段扫过的面积.(结果保留)
16.如图,是的直径,弦于点E,点M在上,恰好经过圆心O,连接.
(1)根据条件,写出一对相等的线段或相等的角;
(2)若,求的半径;
(3)若的半径是(2)中求得的半径,且,求的长.
17.如图,是的直径,是的弦,连接、、,其中,平分,过点B作交的延长线于E.
(1)求证:是的切线;
(2)若,,求图中阴影部分的面积.
参考答案
1--8BCDAA BBB
9.4
10.150
11.
12.
13.8
14.解:由题意得,
在中,
答:该圆锥的侧面积为.
15.(1)解:如图所示,△.
即为所求;
(2)解:,,
旋转时线段扫过的面积.
16.(1)∵是的直径,弦于点E,
∴;
(2)设的半径为r,
∵,
∴,
在中,,,
∵,
∴,解得,
∴的半径为10;
(3)如图,连接,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∴的长为.
17.(1)证明:∵平分,
∴
∵
∴
∴
∴
∵
∴
∴是的切线
(2)过点O作于H,连接,
则,,
∵,
∴四边形是矩形,
∴,,
∵,且,
∴,
∵,
∴,
∵,
∴,
∴,
∵
∴,
∴,
∴,
∴,,
∴,
∴,
∴
.
一、单选题
1.如图,两个大小一样的传送轮连接着一条传送带,则这条传送带的长为( )
A. B. C. D.
2.若圆锥的底面半径为3,母线长为5,则这个圆锥的侧面积为( )
A.15 B.12π C.15π D.30π
3.如图,在中,,,则图中阴影部分的面积为( )
A. B. C. D.
4.如图,是等腰直角三角形,,,把绕点A沿顺时针方向旋转45°后得到,则线段在上述旋转过程中所扫过的部分(阴影部分)的面积是( )
A. B. C. D.
5.数学课上,老师将如图边长为1的正方形铁丝框变形成以A为圆心,为半径的扇形(铁丝的粗细忽略不计),则所得扇形DAB的面积是( )
A.1 B.1.5 C.2 D.
6.如图,将腰长为的等腰绕点旋转至的位置,使、、三点在同一条直线上,则点经过的最短路线长是( )
A. B. C. D.
7.一个扇形的弧长是,半径是4,则该扇形的圆心角的度数是( )
A. B. C. D.
8.一个扇形的面积为.弧长为.那么这个扇形的半径是( )
A.20 B.24 C.26 D.32
二、填空题
9.圆锥的侧面积为,母线长为5.则这个圆锥的底面半径为 .
10.已知圆锥底面积是30平方厘米,高是15厘米,则这个圆锥的体积为 立方厘米.
11.一个圆锥的底面半径为,侧面展开图是半圆,则该圆锥的高是 .
12.已知圆锥底面圆的周长为,圆锥的母线为3,则该圆锥的侧面展开图的圆心角为 .
13.如图,圆锥的底面半径为,母线长为,一只蜘蛛从底面圆周上一点出发沿圆锥的侧面爬行一周后回到点处的最短路程是 .
三、解答题
14.如图,圆锥的底面半径,高,求该圆锥的侧面积.
15.如图,在正方形网格中,每个小正方形的边长都是1个单位长度,的三个顶点坐标分别为,,.
(1)画出绕点逆时针旋转后的△.
(2)在(2)的条件下,求线段扫过的面积.(结果保留)
16.如图,是的直径,弦于点E,点M在上,恰好经过圆心O,连接.
(1)根据条件,写出一对相等的线段或相等的角;
(2)若,求的半径;
(3)若的半径是(2)中求得的半径,且,求的长.
17.如图,是的直径,是的弦,连接、、,其中,平分,过点B作交的延长线于E.
(1)求证:是的切线;
(2)若,,求图中阴影部分的面积.
参考答案
1--8BCDAA BBB
9.4
10.150
11.
12.
13.8
14.解:由题意得,
在中,
答:该圆锥的侧面积为.
15.(1)解:如图所示,△.
即为所求;
(2)解:,,
旋转时线段扫过的面积.
16.(1)∵是的直径,弦于点E,
∴;
(2)设的半径为r,
∵,
∴,
在中,,,
∵,
∴,解得,
∴的半径为10;
(3)如图,连接,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∴的长为.
17.(1)证明:∵平分,
∴
∵
∴
∴
∴
∵
∴
∴是的切线
(2)过点O作于H,连接,
则,,
∵,
∴四边形是矩形,
∴,,
∵,且,
∴,
∵,
∴,
∵,
∴,
∴,
∵
∴,
∴,
∴,
∴,,
∴,
∴,
∴
.
同课章节目录
