第二章 轴对称培优专题 等腰三角形中常见问题探究同步练习(含解析)
文档属性
| 名称 | 第二章 轴对称培优专题 等腰三角形中常见问题探究同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 19:51:09 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 轴对称
培优专题 等腰三角形中常见问题探究
类型一 等腰三角形中的分类讨论思想
1.已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为( )
A.8或10 B.8 C.10 D.6或12
2.若等腰三角形中有一个角等于40°,则这个等腰三角形的顶角度数为( )
A.40° B.100° C.40°或70° D.40°或100°
3.已知△ABC的三边长分别为4,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )
A.3条 B.4条 C.5条 D.6条
4.如图,在 Rt△ABC中,∠ACB=90°,∠ABC=60°,在直线 BC 或 AC 上取一点 P,使得 △APB为等腰三角形,则符合条件的点 P共有( )
A.7个 B.6个 C.5个 D.4个
5.等腰三角形的两个内角的比是1:2,则这个等腰三角形的顶角的度数是__________.
6.过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角度数为_____________.
7.等腰三角形一腰上的高与另一腰的夹角为35°,求这个三角形的各个内角的度数.
8.在△ABC中,AB=AC,AB边的垂直平分线与AC所在的直线相交所得的锐角为40°.求∠B的度数.
类型二 等腰三角形中常见辅助线添加
9.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N 在边 OB 上,PM=PN,若MN=5,则 OM的长度为__________.
10.阅读材料:
如图,在△ABC中,AB=AC,P为底边 BC上任意一点,点 P到两腰的距离分别为r ,r ,腰上的高为h,连接AP,则 即 所以r +r =h(定值).
类比与推理
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即已知等边△ABC内任意一点P到各边的距离分别为 r ,r ,r ,等边△ABC的高为h,试说明:r +r +r =h((定值).
参考答案
1. C 2. D
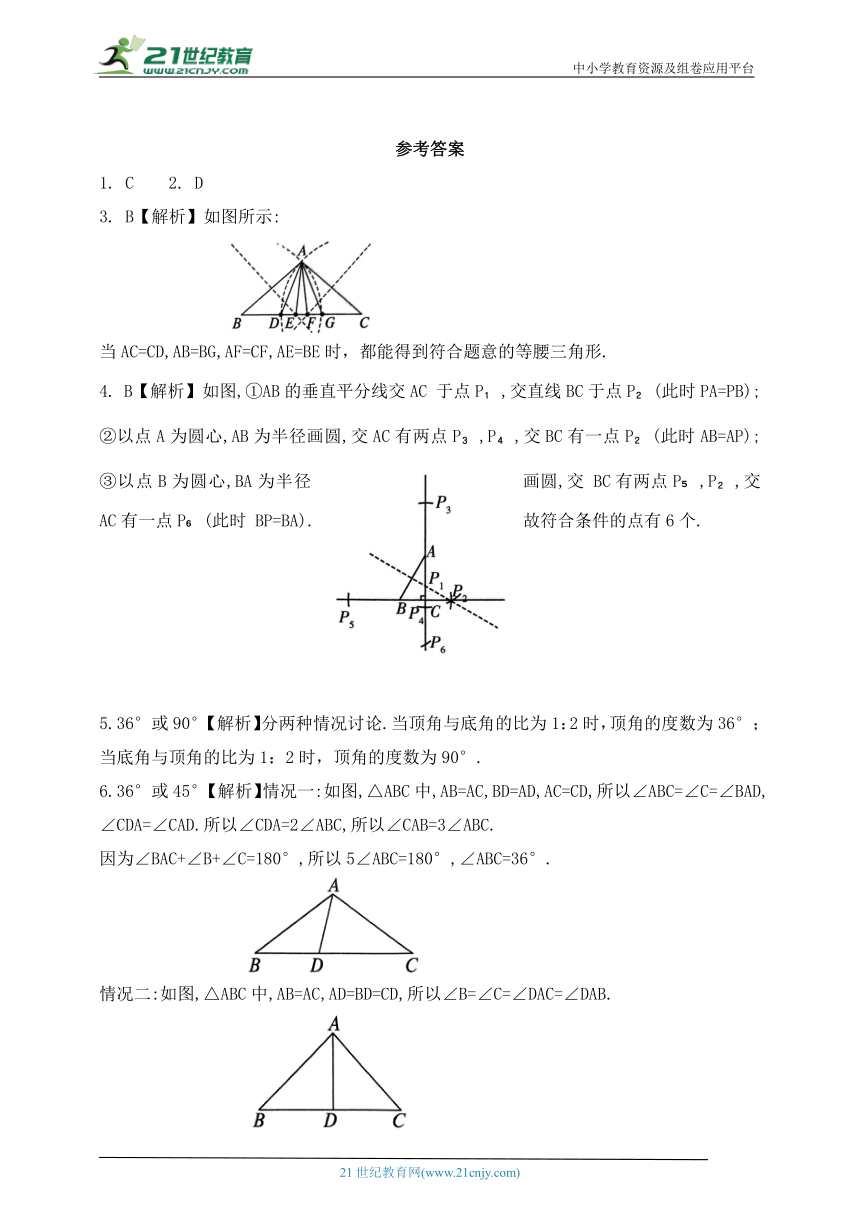
3. B【解析】如图所示:
当AC=CD,AB=BG,AF=CF,AE=BE时,都能得到符合题意的等腰三角形.
4. B【解析】如图,①AB的垂直平分线交AC 于点P ,交直线BC于点P (此时PA=PB);②以点A为圆心,AB为半径画圆,交AC有两点P ,P ,交BC有一点P (此时AB=AP);③以点B为圆心,BA为半径画圆,交 BC有两点P ,P ,交 AC有一点P (此时 BP=BA).故符合条件的点有6个.
5.36°或90°【解析】分两种情况讨论.当顶角与底角的比为1:2时,顶角的度数为36°;当底角与顶角的比为1:2时,顶角的度数为90°.
6.36°或45°【解析】情况一:如图,△ABC中,AB=AC,BD=AD,AC=CD,所以∠ABC=∠C=∠BAD,∠CDA=∠CAD.所以∠CDA=2∠ABC,所以∠CAB=3∠ABC.
因为∠BAC+∠B+∠C=180°,所以5∠ABC=180°,∠ABC=36°.
情况二:如图,△ABC中,AB=AC,AD=BD=CD,所以∠B=∠C=∠DAC=∠DAB.
因为∠BAC+∠B+∠C=180°,所以4∠ABC=180°,∠ABC=45°.
故答案为36°或45°.
7.解:①此等腰三角形为钝角三角形时,因为等腰三角形一腰上的高与另一腰的夹角为35°,所以此三角形的顶角=90°+35°=125°.所以底角=(180°-125°)÷2=27.5°.
所以等腰三角形的各角的度数分别为125°,27.5°,27.5°.
②此等腰三角形为锐角三角形时,因为等腰三角形一腰上的高与另一腰的夹角为35°,所以此三角形的顶角=90°-35°=55°.所以底角=(180°-55°)÷2=62.5°.
所以等腰三角形的各角的度数分别为55°,62.5°,62.5°.
综上所述,等腰三角形的各个内角的度数为125°,27.5°,
27.5°或55°,62.5°,62.5°.
8.解:如图1,当△ABC为锐角三角形时,设AB的垂直平分线交线段AC于点D,交AB于点E.
因为∠ADE=40°,DE⊥AB,所以∠A=90°-40°=50°.
因为AB=AC,所以
如图2,当△ABC为钝角三角形时,设AB的垂直平分线交AB于点E,交CA的延长线于点 D.
因为∠ADE=40°,DE⊥AB,所以∠DAB=50°.
因为AB=AC,所以∠B=∠C.
因为∠B+∠C=∠DAB,所以∠B=25°.
综上可知∠B的度数为65°或25°.
9.3.5 【解析】如图,作PH⊥MN于点H.
因为∠AOB=60°,所以∠OPH=30°.所以
因为PM=PN,PH⊥MN,所以
所以OM=OH-MH=3.5.
10.解:如图,连接AP,BP,CP,则
即
因为△ABC是等边三角形,所以AB=BC=AC.所以r +r +r =h(定值).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 轴对称
培优专题 等腰三角形中常见问题探究
类型一 等腰三角形中的分类讨论思想
1.已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为( )
A.8或10 B.8 C.10 D.6或12
2.若等腰三角形中有一个角等于40°,则这个等腰三角形的顶角度数为( )
A.40° B.100° C.40°或70° D.40°或100°
3.已知△ABC的三边长分别为4,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )
A.3条 B.4条 C.5条 D.6条
4.如图,在 Rt△ABC中,∠ACB=90°,∠ABC=60°,在直线 BC 或 AC 上取一点 P,使得 △APB为等腰三角形,则符合条件的点 P共有( )
A.7个 B.6个 C.5个 D.4个
5.等腰三角形的两个内角的比是1:2,则这个等腰三角形的顶角的度数是__________.
6.过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角度数为_____________.
7.等腰三角形一腰上的高与另一腰的夹角为35°,求这个三角形的各个内角的度数.
8.在△ABC中,AB=AC,AB边的垂直平分线与AC所在的直线相交所得的锐角为40°.求∠B的度数.
类型二 等腰三角形中常见辅助线添加
9.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N 在边 OB 上,PM=PN,若MN=5,则 OM的长度为__________.
10.阅读材料:
如图,在△ABC中,AB=AC,P为底边 BC上任意一点,点 P到两腰的距离分别为r ,r ,腰上的高为h,连接AP,则 即 所以r +r =h(定值).
类比与推理
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即已知等边△ABC内任意一点P到各边的距离分别为 r ,r ,r ,等边△ABC的高为h,试说明:r +r +r =h((定值).
参考答案
1. C 2. D
3. B【解析】如图所示:
当AC=CD,AB=BG,AF=CF,AE=BE时,都能得到符合题意的等腰三角形.
4. B【解析】如图,①AB的垂直平分线交AC 于点P ,交直线BC于点P (此时PA=PB);②以点A为圆心,AB为半径画圆,交AC有两点P ,P ,交BC有一点P (此时AB=AP);③以点B为圆心,BA为半径画圆,交 BC有两点P ,P ,交 AC有一点P (此时 BP=BA).故符合条件的点有6个.
5.36°或90°【解析】分两种情况讨论.当顶角与底角的比为1:2时,顶角的度数为36°;当底角与顶角的比为1:2时,顶角的度数为90°.
6.36°或45°【解析】情况一:如图,△ABC中,AB=AC,BD=AD,AC=CD,所以∠ABC=∠C=∠BAD,∠CDA=∠CAD.所以∠CDA=2∠ABC,所以∠CAB=3∠ABC.
因为∠BAC+∠B+∠C=180°,所以5∠ABC=180°,∠ABC=36°.
情况二:如图,△ABC中,AB=AC,AD=BD=CD,所以∠B=∠C=∠DAC=∠DAB.
因为∠BAC+∠B+∠C=180°,所以4∠ABC=180°,∠ABC=45°.
故答案为36°或45°.
7.解:①此等腰三角形为钝角三角形时,因为等腰三角形一腰上的高与另一腰的夹角为35°,所以此三角形的顶角=90°+35°=125°.所以底角=(180°-125°)÷2=27.5°.
所以等腰三角形的各角的度数分别为125°,27.5°,27.5°.
②此等腰三角形为锐角三角形时,因为等腰三角形一腰上的高与另一腰的夹角为35°,所以此三角形的顶角=90°-35°=55°.所以底角=(180°-55°)÷2=62.5°.
所以等腰三角形的各角的度数分别为55°,62.5°,62.5°.
综上所述,等腰三角形的各个内角的度数为125°,27.5°,
27.5°或55°,62.5°,62.5°.
8.解:如图1,当△ABC为锐角三角形时,设AB的垂直平分线交线段AC于点D,交AB于点E.
因为∠ADE=40°,DE⊥AB,所以∠A=90°-40°=50°.
因为AB=AC,所以
如图2,当△ABC为钝角三角形时,设AB的垂直平分线交AB于点E,交CA的延长线于点 D.
因为∠ADE=40°,DE⊥AB,所以∠DAB=50°.
因为AB=AC,所以∠B=∠C.
因为∠B+∠C=∠DAB,所以∠B=25°.
综上可知∠B的度数为65°或25°.
9.3.5 【解析】如图,作PH⊥MN于点H.
因为∠AOB=60°,所以∠OPH=30°.所以
因为PM=PN,PH⊥MN,所以
所以OM=OH-MH=3.5.
10.解:如图,连接AP,BP,CP,则
即
因为△ABC是等边三角形,所以AB=BC=AC.所以r +r +r =h(定值).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
