第二章 轴对称章末复习题(含解析)
图片预览

文档简介
中小学教育资源及组卷应用平台
第二章 轴对称
章末复习
考点整合
考点1 轴对称图形的判断
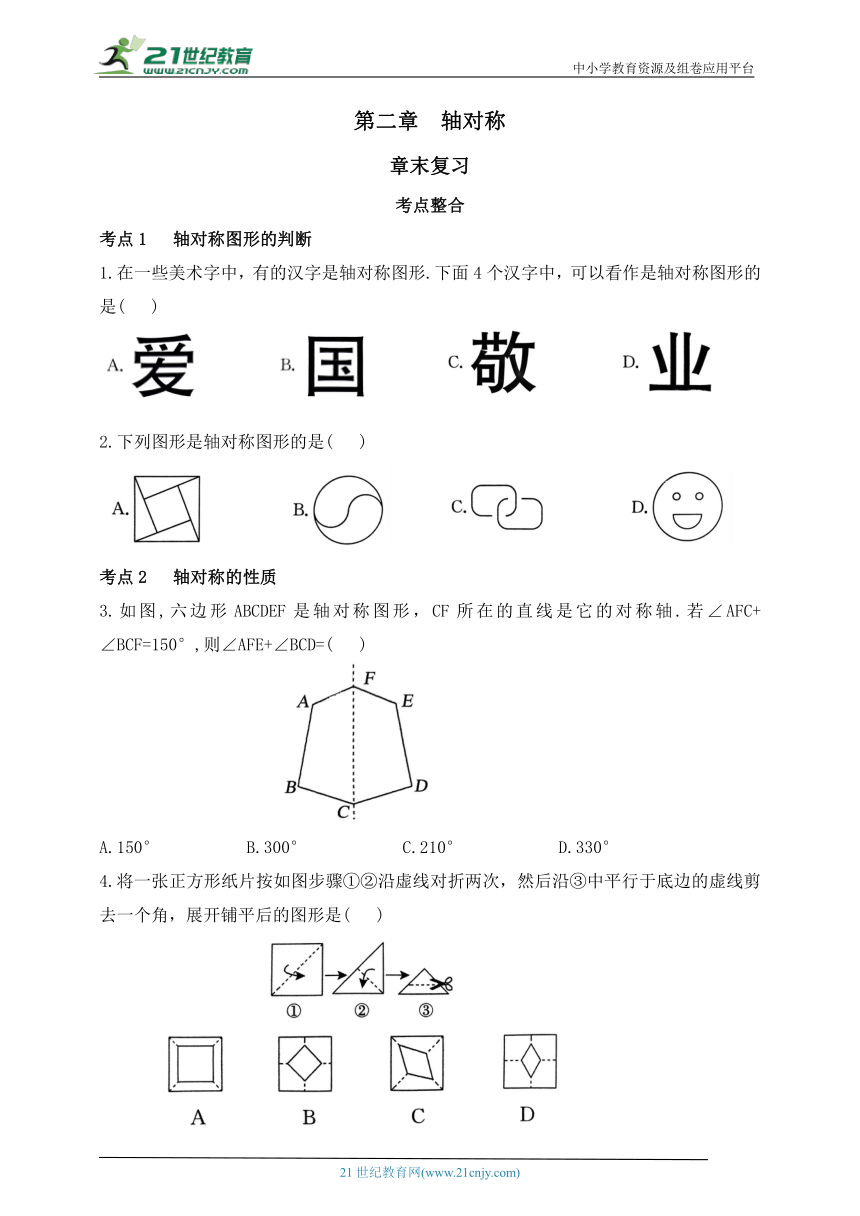
1.在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
2.下列图形是轴对称图形的是( )
考点2 轴对称的性质
3.如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴.若∠AFC+ ∠BCF=150°,则∠AFE+∠BCD=( )
A.150° B.300° C.210° D.330°
4.将一张正方形纸片按如图步骤①②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )
5.如图,点 P为∠AOB内一点,分别作出点 P关于OA,OB的对称点 P ,P ,连接P1P2交OA 于点 M,交 OB于点N.若P P =6,则△PMN 的周长为___________.
考点3 线段垂直平分线与角平分线的性质
6.如图,在△ABC中,DE是AC的垂直平分线,且分别交 BC,AC于点D,E,若∠B=60°,∠C=25°,则∠BAD的度数为( )
A.50° B.70° C.75° D.80°
7.如图,在△ABC中,AB=AC,以点 B为圆心,适当长为半径画弧,交 BA于点M,交 BC于点 N,分别以点 M,N为圆心,大于 的长为半径画弧,两弧在∠ABC的内部相交于点 P,画射线BP,交AC于点D,若AD=BD,则∠A的度数是( )
A.36° B.54° C.72° D.108°
8.如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则
考点4 等腰(边)三角形的性质与判定
9.如图,直线m∥n,△ABC是等边三角形,顶点 B在直线n上,直线m交AB于点E,交AC于点F,若∠1=140°,则∠2的度数是( )
A.80° B.100° C.120° D.140°
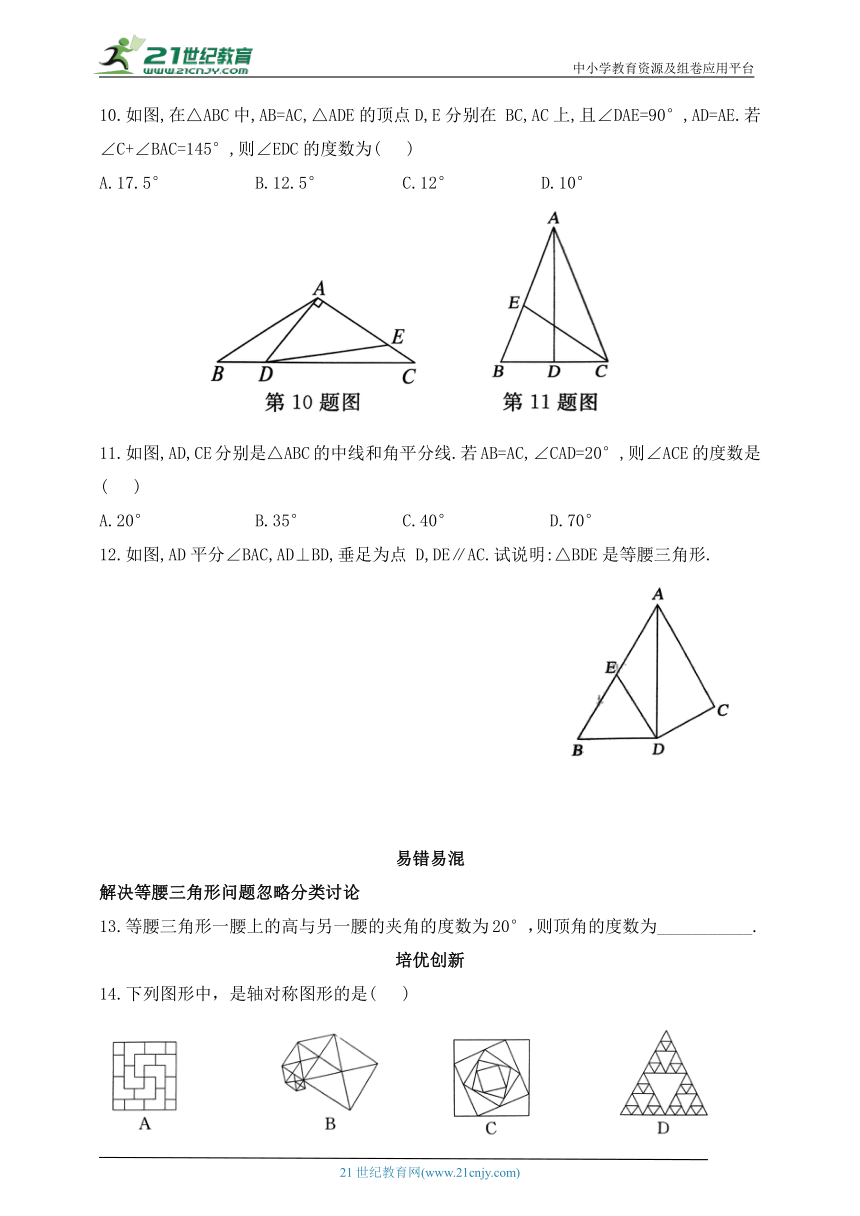
10.如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在 BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )
A.17.5° B.12.5° C.12° D.10°
11.如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
12.如图,AD平分∠BAC,AD⊥BD,垂足为点 D,DE∥AC.试说明:△BDE是等腰三角形.
易错易混
解决等腰三角形问题忽略分类讨论
13.等腰三角形一腰上的高与另一腰的夹角的度数为20°,则顶角的度数为___________.
培优创新
14.下列图形中,是轴对称图形的是( )
15.如图,在△ABC中,∠BAC=80°,AB边的垂直平分线交AB 于点 D,交 BC 于点 E,AC边的垂直平分线交AC 于点 F,交 BC于点G,连接AE,AG.则∠EAG的度数为( )
A.15° B.20° C.25° D.30°
16.如图,在△ABC中,点 D在BC边上,BD=AD=AC,E为CD的中点.若∠CAE=16°,则 ∠B=______________.
17.如图,△ABC中,AB=AC,∠B=30°,点O在BC边上运动(O不与B,C重合),点 D在线段AB上,连接AO,OD.点O运动时,始终满足∠AOD=∠B.
(1)当OD∥AC时,判断△AOB的形状并说明理由;
(2)当AO 的最小值为 4时,此时BD=____________;
(3)在点 O的运动过程中,△AOD的形状是等腰三角形时,请求出此时∠BDO的度数.
参考答案
1. D 2. D 3. B 4. A 5.6
6. B【解析】因为DE是AC的垂直平分线,所以DA=DC.所以∠DAC=∠C=25°.
因为∠B=60°,∠C=25°,所以∠BAC=95°.所以∠BAD=∠BAC-∠DAC=70°.
7. A【解析】由题意可得BP为∠ABC的平分线,所以∠ABD=∠CBD.
因为AD=BD,所以∠A=∠ABD.所以∠A=∠ABD=∠CBD.所以∠ABC=2∠A.
因为AB=AC,所以∠ABC=∠C=2∠A.所以∠A+∠ABC+∠C=∠A+2∠A+2∠A=180°.
解得∠A=36°.故选A.
8.1【解析】过点 D作DH⊥AC于点H,如图.
因为AD平分∠BAC,DE⊥AB,DH⊥AC,所以DE=DH=1.所以 故填1.
9. B【解析】因为△ABC是等边三角形,所以∠A=60°.在△AEF中,因为∠1= 180°-∠AFE=∠A+∠AEF=140°,所以∠AEF=140°-60°=80°.所以∠DEB=∠AEF=80°.因为m∥n,
所以∠2+∠DEB=180°,所以∠2=180°-80°=100°.故选B.
10. D 【解析】因为AB=AC,所以∠B=∠C.所以∠B+∠C+∠BAC=2∠C+∠BAC=180°.又因为∠C+∠BAC=145°,所以∠C=35°.因为∠DAE=90°,AD=AE,所以∠AED=45°.所以 ∠EDC=∠AED-∠C=10°.故选D.
11. B【解析】因为AD是△ABC的中线,AB=AC,∠CAD=20°,
所以 (180°-∠CAB)=70°.
因为 CE 是△ABC的角平分线,所
12.解:因为DE∥AC,所以∠CAD=∠ADE.
因为AD平分∠BAC,所以∠CAD=∠DAE.所以∠DAE=∠ADE.
因为AD⊥BD,所以∠DAE+∠B=90°,∠ADE+∠BDE=90°,所以∠B=∠BDE.
所以BE=DE,即△BDE是等腰三角形.
13.70°或110° 14. D
15. B 【解析】因为AB边的垂直平分线交BC于点E,AC边的垂直平分线交 BC 于点G,所以AE=BE,AG=CG.所以∠B=∠BAE,∠C=∠CAG.
所以∠BAE+∠CAG=∠B+∠C=180°-∠BAC=100°,
所以∠EAG=∠BAE+∠CAG-∠BAC=100°-80°=20°.故选B.
16.37°【解析】因为AD=AC,E是CD的中点,所以AE⊥CD.所以∠AEC=90°.
所以∠C=90°-∠CAE=74°.因为AD=AC,所以∠ADC=∠C=74°.
因为AD=BD,所以2∠B=180°-∠ADB=∠ADC=74°.所以∠B=37°.
17.解:(1)结论:△AOB为直角三角形.
理由:因为AB=AC,∠B=30°,所以∠C=∠B=30°.所以∠BAC=180°-30°-30°=120°.
因为OD∥AC,∠AOD=∠B=30°,所以∠OAC=∠AOD=30°.
所以∠BAO=∠BAC-∠OAC=120°-30°=90°.所以△AOB是直角三角形.
(2)6
【解析】当 AO⊥BC时,OA的值最小,如图.
在Rt△ABO中,∠AOB=90°,AO=4,∠B=30°,所以AB=2OA=8.
因为AB=AC,AO⊥BC,所以∠BAO=90°-30°=60°.
因为∠AOD=∠B=30°,所以∠ADO=180°-60°-30°=90°.
所以 所以BD=AB-AD=8-2=6.
(3)分三种情况:
①当DA=DO时,∠OAD=∠AOD=30°,所以∠BDO=∠OAD+∠AOD=60°.
②当 OA=OD 时, =75°,
所以∠BDO=180°-75°=105°.
③当AD=AO时,∠ADO=∠AOD=30°,
所以∠OAD=120°=∠BAC,点O与C重合,不合题意.
综上所述,∠BDO的度数为60°或105°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 轴对称
章末复习
考点整合
考点1 轴对称图形的判断
1.在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
2.下列图形是轴对称图形的是( )
考点2 轴对称的性质
3.如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴.若∠AFC+ ∠BCF=150°,则∠AFE+∠BCD=( )
A.150° B.300° C.210° D.330°
4.将一张正方形纸片按如图步骤①②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )
5.如图,点 P为∠AOB内一点,分别作出点 P关于OA,OB的对称点 P ,P ,连接P1P2交OA 于点 M,交 OB于点N.若P P =6,则△PMN 的周长为___________.
考点3 线段垂直平分线与角平分线的性质
6.如图,在△ABC中,DE是AC的垂直平分线,且分别交 BC,AC于点D,E,若∠B=60°,∠C=25°,则∠BAD的度数为( )
A.50° B.70° C.75° D.80°
7.如图,在△ABC中,AB=AC,以点 B为圆心,适当长为半径画弧,交 BA于点M,交 BC于点 N,分别以点 M,N为圆心,大于 的长为半径画弧,两弧在∠ABC的内部相交于点 P,画射线BP,交AC于点D,若AD=BD,则∠A的度数是( )
A.36° B.54° C.72° D.108°
8.如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则
考点4 等腰(边)三角形的性质与判定
9.如图,直线m∥n,△ABC是等边三角形,顶点 B在直线n上,直线m交AB于点E,交AC于点F,若∠1=140°,则∠2的度数是( )
A.80° B.100° C.120° D.140°
10.如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在 BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )
A.17.5° B.12.5° C.12° D.10°
11.如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
12.如图,AD平分∠BAC,AD⊥BD,垂足为点 D,DE∥AC.试说明:△BDE是等腰三角形.
易错易混
解决等腰三角形问题忽略分类讨论
13.等腰三角形一腰上的高与另一腰的夹角的度数为20°,则顶角的度数为___________.
培优创新
14.下列图形中,是轴对称图形的是( )
15.如图,在△ABC中,∠BAC=80°,AB边的垂直平分线交AB 于点 D,交 BC 于点 E,AC边的垂直平分线交AC 于点 F,交 BC于点G,连接AE,AG.则∠EAG的度数为( )
A.15° B.20° C.25° D.30°
16.如图,在△ABC中,点 D在BC边上,BD=AD=AC,E为CD的中点.若∠CAE=16°,则 ∠B=______________.
17.如图,△ABC中,AB=AC,∠B=30°,点O在BC边上运动(O不与B,C重合),点 D在线段AB上,连接AO,OD.点O运动时,始终满足∠AOD=∠B.
(1)当OD∥AC时,判断△AOB的形状并说明理由;
(2)当AO 的最小值为 4时,此时BD=____________;
(3)在点 O的运动过程中,△AOD的形状是等腰三角形时,请求出此时∠BDO的度数.
参考答案
1. D 2. D 3. B 4. A 5.6
6. B【解析】因为DE是AC的垂直平分线,所以DA=DC.所以∠DAC=∠C=25°.
因为∠B=60°,∠C=25°,所以∠BAC=95°.所以∠BAD=∠BAC-∠DAC=70°.
7. A【解析】由题意可得BP为∠ABC的平分线,所以∠ABD=∠CBD.
因为AD=BD,所以∠A=∠ABD.所以∠A=∠ABD=∠CBD.所以∠ABC=2∠A.
因为AB=AC,所以∠ABC=∠C=2∠A.所以∠A+∠ABC+∠C=∠A+2∠A+2∠A=180°.
解得∠A=36°.故选A.
8.1【解析】过点 D作DH⊥AC于点H,如图.
因为AD平分∠BAC,DE⊥AB,DH⊥AC,所以DE=DH=1.所以 故填1.
9. B【解析】因为△ABC是等边三角形,所以∠A=60°.在△AEF中,因为∠1= 180°-∠AFE=∠A+∠AEF=140°,所以∠AEF=140°-60°=80°.所以∠DEB=∠AEF=80°.因为m∥n,
所以∠2+∠DEB=180°,所以∠2=180°-80°=100°.故选B.
10. D 【解析】因为AB=AC,所以∠B=∠C.所以∠B+∠C+∠BAC=2∠C+∠BAC=180°.又因为∠C+∠BAC=145°,所以∠C=35°.因为∠DAE=90°,AD=AE,所以∠AED=45°.所以 ∠EDC=∠AED-∠C=10°.故选D.
11. B【解析】因为AD是△ABC的中线,AB=AC,∠CAD=20°,
所以 (180°-∠CAB)=70°.
因为 CE 是△ABC的角平分线,所
12.解:因为DE∥AC,所以∠CAD=∠ADE.
因为AD平分∠BAC,所以∠CAD=∠DAE.所以∠DAE=∠ADE.
因为AD⊥BD,所以∠DAE+∠B=90°,∠ADE+∠BDE=90°,所以∠B=∠BDE.
所以BE=DE,即△BDE是等腰三角形.
13.70°或110° 14. D
15. B 【解析】因为AB边的垂直平分线交BC于点E,AC边的垂直平分线交 BC 于点G,所以AE=BE,AG=CG.所以∠B=∠BAE,∠C=∠CAG.
所以∠BAE+∠CAG=∠B+∠C=180°-∠BAC=100°,
所以∠EAG=∠BAE+∠CAG-∠BAC=100°-80°=20°.故选B.
16.37°【解析】因为AD=AC,E是CD的中点,所以AE⊥CD.所以∠AEC=90°.
所以∠C=90°-∠CAE=74°.因为AD=AC,所以∠ADC=∠C=74°.
因为AD=BD,所以2∠B=180°-∠ADB=∠ADC=74°.所以∠B=37°.
17.解:(1)结论:△AOB为直角三角形.
理由:因为AB=AC,∠B=30°,所以∠C=∠B=30°.所以∠BAC=180°-30°-30°=120°.
因为OD∥AC,∠AOD=∠B=30°,所以∠OAC=∠AOD=30°.
所以∠BAO=∠BAC-∠OAC=120°-30°=90°.所以△AOB是直角三角形.
(2)6
【解析】当 AO⊥BC时,OA的值最小,如图.
在Rt△ABO中,∠AOB=90°,AO=4,∠B=30°,所以AB=2OA=8.
因为AB=AC,AO⊥BC,所以∠BAO=90°-30°=60°.
因为∠AOD=∠B=30°,所以∠ADO=180°-60°-30°=90°.
所以 所以BD=AB-AD=8-2=6.
(3)分三种情况:
①当DA=DO时,∠OAD=∠AOD=30°,所以∠BDO=∠OAD+∠AOD=60°.
②当 OA=OD 时, =75°,
所以∠BDO=180°-75°=105°.
③当AD=AO时,∠ADO=∠AOD=30°,
所以∠OAD=120°=∠BAC,点O与C重合,不合题意.
综上所述,∠BDO的度数为60°或105°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
