北师大版八年级数学上册试题 4.4一次函数的应用(含答案)
文档属性
| 名称 | 北师大版八年级数学上册试题 4.4一次函数的应用(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 345.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 00:00:00 | ||
图片预览



文档简介
4.4一次函数的应用
一.选择题
1.如图,一个条形测力计不挂重物时长5cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比,弹簧总长y(cm)关于所挂物体质量x(kg)的函数图象如图所示,则图中a的值是( )
A.15 B.18 C.20 D.33
2.如图是甲、乙两个动点在某时段速度随时间变化的图象,下列结论错误的是( )
A.点乙前3秒运动的路程为36cm
B.甲、乙两点到第3秒时运动的路程相等
C.甲、乙两点在第3秒时的速度相等
D.在4至8秒内甲的速度都大于乙的速度
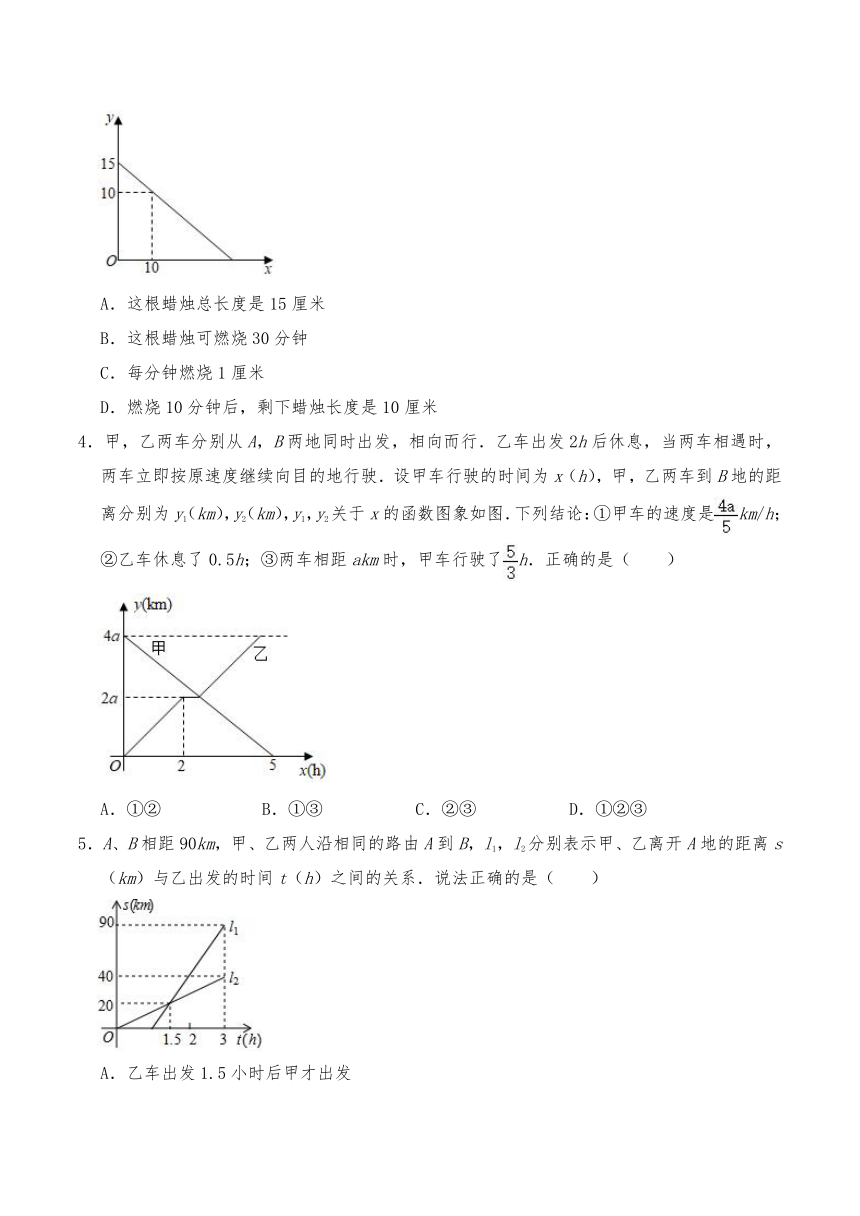
3.一根粗细均匀的蜡烛,开始燃烧后,剩下的长度y(厘米)与燃烧的时间x(分钟)的关系如图所示,根据图象得到下列信息,错误的是( )
A.这根蜡烛总长度是15厘米
B.这根蜡烛可燃烧30分钟
C.每分钟燃烧1厘米
D.燃烧10分钟后,剩下蜡烛长度是10厘米
4.甲,乙两车分别从A,B两地同时出发,相向而行.乙车出发2h后休息,当两车相遇时,两车立即按原速度继续向目的地行驶.设甲车行驶的时间为x(h),甲,乙两车到B地的距离分别为y1(km),y2(km),y1,y2关于x的函数图象如图.下列结论:①甲车的速度是km/h;②乙车休息了0.5h;③两车相距akm时,甲车行驶了h.正确的是( )
A.①② B.①③ C.②③ D.①②③
5.A、B相距90km,甲、乙两人沿相同的路由A到B,l1,l2分别表示甲、乙离开A地的距离s(km)与乙出发的时间t(h)之间的关系.说法正确的是( )
A.乙车出发1.5小时后甲才出发
B.两人相遇时,他们离开A地40km
C.甲的速度是30km/h
D.乙的速度是km/h
6.AB两地相距20km,甲从A地出发向B地前进,乙从B地出发向A地前进,两人沿同一直线同时出发,甲先以8km/h的速度前进1小时,然后减慢速度继续匀速前进,甲乙两人离A地的距离s(km)与时间t(h)的关系如图所示,则甲出发( )小时后与乙相遇.
A.1.5 B.2 C.2.5 D.3
7.一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:
①A,B两村相距10km;②甲出发2h后到达C村;③甲每小时比乙多骑行8km;④相遇后,乙又骑行了30min或55min时两人相距4km.其中正确的是( )
A.①③④ B.①②③ C.①②④ D.①②③④
二.填空题
8.某生态体验园推出了甲、乙两种消费卡.甲、乙两卡所需费用y甲,y乙(单位:元)与入园次数x(单位:次)的函数关系如图所示.当x满足 时,y甲>y乙.
9.甲骑电动车从A地以匀速前往B地,到达B地后停止,在甲车出发的同时乙骑助力车从B地匀速前往A地,到达A地后停止,甲的速度比乙快.两人之间的距离y(千米)与甲出发的时间x(分钟)的函数关系如图所示,根据图象得出下列信息:
①A,B两地相距15千米;
②甲从A地到B地用了45分钟;
③甲到达B地时,乙离A地还有4千米;
④甲骑电动车的速度为25千米/时.
其中正确的是 .(写出所有正确的序号)
10.A、B两地相距480千米,甲车从A地匀速前往B地,乙车同时从B地沿同一公路匀速前往A地.甲车出发30分钟时发现自己有物件落在A地,于是立即掉头以原速返回取件,取件后立即掉头以原速继续匀速前行(掉头和取件时间忽略不计),两车之间相距的路程y(km)与甲车出发时间t(h)之间的函数关系如图所示.则当甲车到达B地时,乙车离A地的路程为 千米.
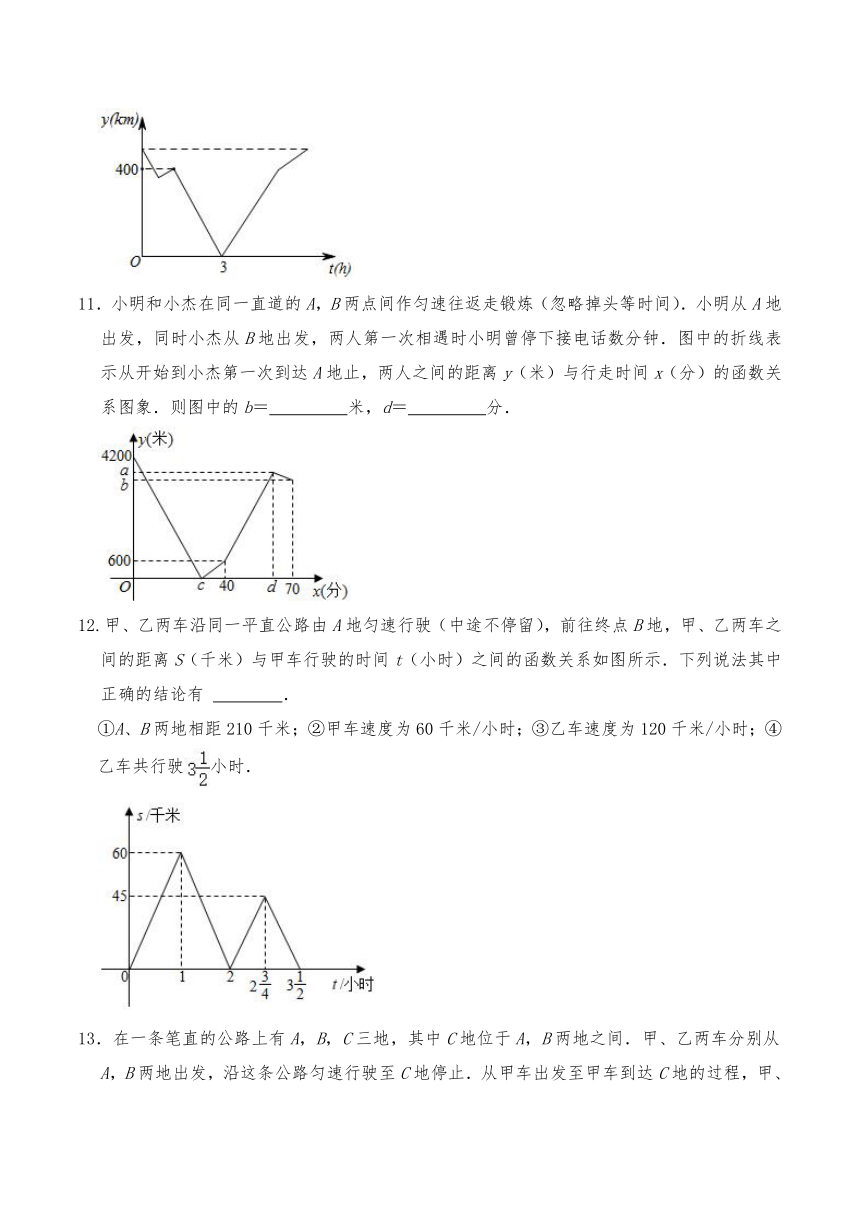
11.小明和小杰在同一直道的A,B两点间作匀速往返走锻炼(忽略掉头等时间).小明从A地出发,同时小杰从B地出发,两人第一次相遇时小明曾停下接电话数分钟.图中的折线表示从开始到小杰第一次到达A地止,两人之间的距离y(米)与行走时间x(分)的函数关系图象.则图中的b= 米,d= 分.
12.甲、乙两车沿同一平直公路由A地匀速行驶(中途不停留),前往终点B地,甲、乙两车之间的距离S(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.下列说法其中正确的结论有 .
①A、B两地相距210千米;②甲车速度为60千米/小时;③乙车速度为120千米/小时;④乙车共行驶小时.
13.在一条笔直的公路上有A,B,C三地,其中C地位于A,B两地之间.甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.根据图象可得A,B两地之间的距离为 km;当甲车出发 h时,两车相距300km.
14.甲、乙两车分别从A,B两地同时相向匀速行驶,当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过12小时后两车同时到达距A地300千米的C地(中途休息时间忽略不计).设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则当甲车到达B地时,乙车距A地 千米.
15.甲、乙两小朋友都从A地出发,匀速步行到B地(A、B两地之间为笔直的道路),甲出发半分钟后,乙才从A地出发,经过一段时间追上甲,两人继续向B地步行,当甲、乙之间的距离刚好是70米时,乙立刻掉头以原速度向A地步行,半分钟后与甲相遇,乙又立刻掉头向B地以原速度步行(两次掉头时间忽略不计).甲、乙相距的路程为y(米)与乙出发的时间x(分钟)之间的关系如图所示,当乙到达B地时,甲与B地相距的路程是 米.
16.甲、乙两人在同一条直线跑道AB上进行往返跑,甲从A地出发,乙从A、B之间的C地出发,且比甲晚出发1分钟,甲到达B地后,立即调头返回A地,并将速度降为原速的,而乙到达B地后仍以原速返回A地(甲、乙掉头的时间均忽略不计),两人之间的距离y(米)与甲的时间x(分)之间的部分函数关系如图所示,则当乙到达B地时,甲离A地的距离为 米.
三.解答题
17.小明与小亮进行百米赛跑,小明比小亮跑得快,如果两人同时起跑,小明肯定赢.现在小明让小亮先跑若干米,图中l1,l2分别表示两人在赛跑中的路程与时间的关系(图象不完整).试观察图象并回答下列问题:
(1)哪条线段是表示小明所跑的路程与时间的关系?
(2)小明让小亮先跑了多少米?
(3)谁会赢得这场比赛?
18.某商店销售一种商品,经市场调查发现:当该商品每件售价是50元时,可以销售100件,且利润为1000元;当该商品每件售价是60元时,可以销售80件,且利润为1600元.
(1)该商品每件进价是多少元?
(2)当用字母x表示商品每件售价,用字母y表示商品的销售量时,发现本题中x、y的值总是满足关系式:y=kx+b,请同学们根据题目提供的数据求出k、b的值,并求出当商品每件售价为70元时,销售利润是多少元?
19.抗击疫情,我们在行动.某药店销售A型和B型两种型号的口罩,销售一箱A型口罩可获利120元,销售一箱B型口罩可获利140元.该药店计划一次购进两种型号的口罩共100箱,其中B型口罩的进货量不超过A型口罩的3倍.设购进A型口罩x箱,这100箱口罩的销售总利润为y元.
(1)求y与x的函数关系式;
(2)该商店购进A型、B型口罩各多少箱,才能使销售利润最大?最大利润是多少?
(3)若限定该药店最多购进A型口罩60箱,则这100口罩的销售总利润能否为12540元?请说明理由.
20.如图,在平面直角坐标系中,过点C(0,12)的直线AC与直线OA相交于点A(8,4).
(1)求直线AC的表达式;
(2)求△OAC的面积;
(3)动点M在线段OA和射线AC上运动,是否存在点M,使△OMC的面积是△OAC的面积的?若存在,求出此时点M的坐标;若不存在,请说明理由.
21.如图,平面直角坐标系中,直线y=kx+b经过点A(2,0),D(0,1),点B是第一象限的点且,过点B作BC⊥y轴,垂足为C,CB=1.
(1)直线y=kx+b的解析式;
(2)求点B坐标;
(3)若点M是直线AD上的一个动点,在x轴上存在另一个点N,且以O、B、M、N为顶点的四边形是平行四边形,请直接写出点N的坐标.
22.如图,直线l:y=x+b过点A(﹣3,0),与y轴交于点B,∠OAB的平分线交y轴于点C,过点C作直线AB的垂线,交x轴于点E,垂足是点D.
(1)求点B和点C的坐标;
(2)求直线DE的函数关系式;
(3)设点P是y轴上一动点,当PA+PD的值最小时,请直接写出点P的坐标.
23.某山区的甲乙两地相距240km,一辆货车从甲地出发匀速开往乙地,货车出发2小时后,一辆小汽车从乙地出发匀速开往甲地,两车同时到达各自的目的地.已知两车行驶的路程之和y(km)与货车行驶的时间x(h)之间的函数关系如图所示.
(1)货车的速度是 km/h,a的值为 ,小汽车行驶了 小时到达甲地;
(2)求小汽车出发后y与x之间的函数关系式,并写出b的值;
(3)当两车相距100km时,求货车行驶的时间.
24.如图,在平面直角坐标系中,直线y=x+5与x轴交于点A,与y轴交于点B,过点B的另一直线交x轴正半轴于C,且△ABC面积为15.
(1)求点C的坐标及直线BC的表达式;
(2)若M为线段BC上一点,且△ABM的面积等于△AOB的面积,求M的坐标;
(3)在(2)的条件下,点E为直线AM上一动点,在x轴上是否存在点D,使以点D、E、B、C为顶点的四边形为平行四边形?若存在,直接写出点D的坐标;若不存在,请说明理由.
25.如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,C,经过点C的直线与x轴交于点B(2,0).
(1)求直线BC的解析式;
(2)点P是线段AC上一动点,若直线BP把△ABC的面积分成1:2的两部分,请求点P的坐标;
(3)若点P是直线AC上一动点,点E是坐标轴上一动点,则是否存在动点P使以点B,C,P,E为顶点的四边形是以BC为一边的平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
26.如图,在直角坐标系中放入一个矩形纸片ABCO,BC=10,将纸片翻折后,点B恰好落在x轴上,记为B',折痕为CE,已知OC:OB'=4:3.
(1)求点B'的坐标;
(2)求折痕CE所在直线的解析式;
(3)若点P是y轴上的一个动点,当△CPE为等腰三角形时,请求出点P的坐标.
答案
一.选择题
C.B.C.A.D.B.D.
二.填空题
8.x>10.
9.①④.
10.80.
11.3600,62.5.
12.①②③.
13.480;.
14.100.
15.40.
16..
三.解答题
17.解:(1)l2表示小明所跑的路程与时间的关系;
(2)观察图象可知,小明让小亮先跑了10米;
(3)由图象可知当小明跑了5秒时,小亮跑了40﹣10=30(米),小明跑了35米,
所以小明的速度为:35÷5=7(米/秒),小亮的速度为:30÷5=6(米/秒);
小明到达终点的时间是100÷7=(秒),小亮到达终点的时间是(100﹣10)÷6=15(秒),
∵<15,
∴小明会赢得这场比赛.
18.解:(1)∵100件商品的利润为1000元,
∴一件商品的利润为1000÷100=10(元),
50﹣10=40(元),
∴该商品每件进价是40元;
(2)把x=50,y=100;x=60,y=80分别代入y=kx+b得:
,解得:,
由题意得:,
解得:40≤x≤100,
∴y=﹣2x+200(40≤x≤100),
当x=70元时,y=﹣2×70+200=60,
销售利润为:(70﹣40)×60=1800(元).
∴,
当商品每件售价为70元时,销售利润是1800元.
19.解:(1)根据题意得,
y=120x+140(100﹣x)=﹣20x+14000,
答:y与x的函数关系式为:y=﹣20x+14000;
(2)根据题意得,100﹣x≤3x,解得x≥25,
∵y=﹣20x+14000,k=﹣20<0;
∴y随x的增大而减小,
∵x为正整数,
∴当x=25时,y取最大值为﹣20×25+14000=13500,则100﹣x=75,
即商店购进A型口罩25箱、B型口罩75箱,才能使销售总利润最大,最大利润为13500元;
(3)根据题意得25≤x≤60,
∵y=﹣20x+14000,k=﹣20<0;
∴y随x的增大而减小,
∵x为正整数,
∴当x=60时,y取最小值为﹣20×60+14000=12800,
∵12800>12540,
∴这100箱口罩的销售总利润不能为12540元.
20.解:(1)设直线AC解析式为y=kx+b,
将C(0,12),A(8,4)代入得:
,解得,
∴直线AC解析式为y=﹣x+12;
(2)过A作AH⊥OC于H,如图:
∵A(8,4),AH⊥OC,
∴AH=8,
∵C(0,12),
∴OC=12,
∴S△OAC=OC AH=×12×8=48;
(3)存在,
①若M在线段OA上时,如图:
∵△OMC的面积是△OAC的面积的,
∴M为OA中点,
而A(8,4),
∴M(4,2),
②当M在射线AC上时,如图:
∵△OMC的面积是△OAC的面积的,
∴M为AC的中点,
而A(8,4),C(0,12),
∴M(4,8),
由等底同高的三角形面积相等可知,若M在C上方的射线AC上的M'处,CM'=CM时,△OM'C的面积也等于△OAC的面积的,
此时C为线段MM'的中点,
而C(0,12),M(4,8),
∴M'(﹣4,16),
综上所述,M的坐标为:(4,2)或(4,8)或(﹣4,16).
21.解:(1)∵A(2,0),D(0,1),
将点A、D的坐标代入y=kx+b得:
,
解得:,
∴直线y=kx+b的解析式:y=﹣x+1;
(2)∵BC=1,BC⊥y轴,
∴设B(1,m),
∵AB=,
∴1+m2=5,
解得m=2(负值舍去),
∴B(1,2);
(3)∵点N在x轴上,O、B、M、N为顶点的四边形是平行四边形,
∴BM∥x轴,且BM=ON,
根据(1),点B的坐标为(1,2),
∴﹣x+1=2,
解得x=﹣2,
∴点M的坐标为(﹣2,2),
∴BM=1﹣(﹣2)=1+2=3,
①点N在点O的左边时,ON=BM=3,
∴点N的坐标为(﹣3,0),
②点N在点O的右边时,ON=BM=3,
∴点N的坐标为(3,0),
③作N(﹣3,0)关于A对称的点N′,则N′也符合,
点N′的坐标是(7,0),
综上所述,点N的坐标为(﹣3,0)或(3,0)或(7,0).
22.解:(1)把点A(﹣3,0)代入y=x+b,得b=4,
∴B(0,4),
∴OB=4,
∵A(﹣3,0),
∴OA=3,
在 Rt△AOB中,∠AOB=90°,
∴AB==5.
∵AC平分∠OAB,CD⊥AB,CO⊥OA,
∴CD=CO,∠ACD=∠ACO,
∵AC=AC,
∴△ACD≌△ACO(SAS),
∴AD=AO=3,BD=AB﹣AD=2.
设CD=CO=m,则BC=4﹣m,
在Rt△BDC中,
由勾股定理知,CD2+BD2=BC2,
∴m2+22=(4﹣m)2,
解得,m=,
∴C(0,);
(2)∵CD⊥AB,CO⊥OA,
∴∠CDB=∠COE=90°,
∵CD=CO,∠BCD=∠ECO,
∴△BCD≌△ECO(ASA),
OE=BD=2,
∴E的坐标(2,0),
∵C(0,),
设直线DE的函数关系式为y=kx+,
∴0=2k+,解得:k=﹣,
∴直线DE的函数关系式为y=﹣x+;
(3)作点A关于y轴对称的点A′,连接A′D交y轴于点P,即为所求的点P,此时,PA+PD的值最小,过点D作DF⊥BC于F,
∵CD=CO=,OB=4,
∴BC=,
∵CD⊥AB,BD=2,
∴DF==,
∵直线DE的函数关系式为y=﹣x+,
∴D(﹣,),
∵A(﹣3,0),
∴A′(3,0),
设A′D的解析式为y=k′x+b′,
∴,解得:,
∴A′D的解析式为y=﹣x+,
当x=0时,y=,
∴点P的坐标为(0,).
23.解:(1)由图象可得,
货车的速度是80÷2=40(km/h),
a=240+240=480,
6﹣2=4(小时),
小汽车行驶了4小时到达甲地,
故答案为:40,480,4;
(2)设小汽车出发后y与x之间的函数关系式为y=kx+m,
由题意得:,
解得,
即小汽车出发后y与x之间的函数关系式为y=100x﹣120,
∴当x=3时,y=100×3﹣120=180,
∴b的值为180;
(3)当两车相遇前相距100km时,
y+100=240,
即100x﹣120+100=240,
解得,
当两车相遇后相距100km时,
y﹣100=240,
即100x﹣120﹣100=240,
解得,
24.解:(1)直线y=x+5与x轴交于点A,与y轴交于点B,
∴A(﹣2,0),B(0,5),
即OA=2,OB=5,
∵△ABC面积为15,
∴(OA+OC) OB=15,
∴OC=4,
∴C(4,0),
设直线BC的表达式为y=kx+b,
将点B、C的坐标代入一次函数表达式得:,
解得:,
∴直线BC的表达式为:y=﹣x+5;
(2)∵S△ACM=S△ABC﹣S△ABM=S△ABC﹣S△ABO=15﹣×2×5=10,
∴S△ACM=×6×ym=10,解得:ym=,
解得:xm=,
∴M(,);
(3)∵A(﹣2,0),M(,),
设直线AM的表达式为y=k′x+b′,
将点A、M的坐标代入一次函数表达式得:,
解得:,
∴直线AM的表达式为:y=x+2.
①当BC为平行四边形的边,四边形BCDE为平行四边形时,如图:
∵B(0,5),BE∥CD,BE=CD,
∴点E的纵坐标是5,
∵点E为直线AM上一动点,直线AM的表达式为:y=x+2.
∴x+2=5,解得:x=3,
∴E (3,5),
∴BE=CD=3,
∵C(4,0),
∴D(7,0);
②当BC为平行四边形的边,四边形BDEC为平行四边形时,如图:过点E作EF⊥x轴于F,
∵四边形BDEC为平行四边形,
∴BC=ED,∠DBC=∠CED,BD=EC,
∴△BDC≌△ECD(SAS),
∴EF=OB,
∵B(0,5),
∴EF=OB=5,
∴点E的纵坐标是﹣5,
∵点E为直线AM上一动点,直线AM的表达式为:y=x+2.
∴x+2=﹣5,解得:x=﹣7,
∴OF=7,
在Rt△BOC和Rt△EFD中,
,
∴Rt△BOC≌Rt△EFD(HL),
∴DF=OC,
∵C(4,0),
∴DF=4,
∴OD=4+7=11,
∴D(﹣11,0);
③当BC为平行四边形的对角线时,
∵B(0,5),BE∥CD,BE=CD,
∴点E的纵坐标是5,
∵点E为直线AM上一动点,直线AM的表达式为:y=x+2.
∴x+2=5,解得:x=3,
∴E (3,5),
∴BE=CD=3,
∵C(4,0),
∴D(1,0).
综上,存在,满足条件的点D的坐标为(7,0)或(﹣11,0)或(1,0).
25.解:(1)由得:A(﹣4,0),C(0,﹣2),
设直线BC的解析式为y=kx+b(k≠0):
∴,解得:,
∴直线BC的解析式为y=;
(2)∵A(﹣4,0),C(0,﹣2),B(2,0).
∴AC=6,
∴S△ABC=×6×2=6,
设P(m,),(﹣4<m<0),
①当S△ABP:S△BPC=1:2时,即=,
∴,
∴m=,
∴;
当S△ABP:S△BPC=2:1时,即=,
∴,
∴m=,
∴,
∴;
(3)以点B,C,P,E为顶点的四边形是以BC为一边的平行四边形,
设P(m,)(﹣4<m<0),
①如图,当E在y轴的正半轴上时,C也在y轴上,设对角线PB、CE的交点为Q,则点Q在y轴上,
∵四边形PEBC是平行四边形,
∴PQ=BQ,
∵B(2,0),(m+2)=0,
∴m=﹣2,
代入P(m,)得=﹣,
∴P1(﹣2,﹣);
②如图,当E在y轴的负半轴上时,BP=CE.BP∥y轴,
∵B(2,0),
∴m=2,=﹣3,
∴P2(2,﹣3);
③如图,当E在x轴的负半轴上,EB为对角线,PA=CA.
∵A(﹣4.0),P(m,),C(0.﹣2),
∴(m+0)=﹣4,
解得:m=﹣8,
∴=2,
∴P3(﹣8,2).
综上,存在,P1(﹣2,﹣),P2(2,﹣3),P3(﹣8,2).
26.解:(1)∵四边形OABC是矩形,
∴∠AOC=90°,
∵OC:OB'=4:3,
设OC=4x,则OB'=3x,
∴B'C==5x,
∵B'C=BC=10,
即5x=10,
解得x=2,
∴OB'=3x=6,
∴B'(6,0);
(2)由(1)知,OC=4x=8,
∴C(0,8),
设AE=a,则BE=B'E=8﹣a,AB'=AO﹣OB'=10﹣6=4,
由勾股定理,得AE2+AB'2=BE'2,
即a2+42=(8﹣a)2,
解得a=3,
∴E点坐标为(10,3),
设直线CE的解析式为y=kx+b,
代入C点和E点坐标,得,
解得,
∴CE所在的直线解析式为y=﹣x+8;
(3)由(2)知,C(0,8),E(10,3),
设P(0,t),
则CE==5,CP=|8﹣t|,EP=,
若△CPE为等腰三角形,分以下三种情况:
①当CP=CE时,
即|8﹣t|=5,
∴t=8+5或8﹣5,
故P点坐标为(8+5,0)或(8﹣5,0);
②当CE=EP时,
即5=,
解得t=﹣2或8,
故P点的坐标为(﹣2,0)或(8,0),
③当CP=EP时,
即|8﹣t|=,
解得t=﹣,
故P点的坐标为(﹣,0);
综上,当△CPE为等腰三角形时,P点的坐标为(8+5,0)或(8﹣5,0)或(﹣2,0)或(8,0)或(﹣,0).
一.选择题
1.如图,一个条形测力计不挂重物时长5cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比,弹簧总长y(cm)关于所挂物体质量x(kg)的函数图象如图所示,则图中a的值是( )
A.15 B.18 C.20 D.33
2.如图是甲、乙两个动点在某时段速度随时间变化的图象,下列结论错误的是( )
A.点乙前3秒运动的路程为36cm
B.甲、乙两点到第3秒时运动的路程相等
C.甲、乙两点在第3秒时的速度相等
D.在4至8秒内甲的速度都大于乙的速度
3.一根粗细均匀的蜡烛,开始燃烧后,剩下的长度y(厘米)与燃烧的时间x(分钟)的关系如图所示,根据图象得到下列信息,错误的是( )
A.这根蜡烛总长度是15厘米
B.这根蜡烛可燃烧30分钟
C.每分钟燃烧1厘米
D.燃烧10分钟后,剩下蜡烛长度是10厘米
4.甲,乙两车分别从A,B两地同时出发,相向而行.乙车出发2h后休息,当两车相遇时,两车立即按原速度继续向目的地行驶.设甲车行驶的时间为x(h),甲,乙两车到B地的距离分别为y1(km),y2(km),y1,y2关于x的函数图象如图.下列结论:①甲车的速度是km/h;②乙车休息了0.5h;③两车相距akm时,甲车行驶了h.正确的是( )
A.①② B.①③ C.②③ D.①②③
5.A、B相距90km,甲、乙两人沿相同的路由A到B,l1,l2分别表示甲、乙离开A地的距离s(km)与乙出发的时间t(h)之间的关系.说法正确的是( )
A.乙车出发1.5小时后甲才出发
B.两人相遇时,他们离开A地40km
C.甲的速度是30km/h
D.乙的速度是km/h
6.AB两地相距20km,甲从A地出发向B地前进,乙从B地出发向A地前进,两人沿同一直线同时出发,甲先以8km/h的速度前进1小时,然后减慢速度继续匀速前进,甲乙两人离A地的距离s(km)与时间t(h)的关系如图所示,则甲出发( )小时后与乙相遇.
A.1.5 B.2 C.2.5 D.3
7.一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:
①A,B两村相距10km;②甲出发2h后到达C村;③甲每小时比乙多骑行8km;④相遇后,乙又骑行了30min或55min时两人相距4km.其中正确的是( )
A.①③④ B.①②③ C.①②④ D.①②③④
二.填空题
8.某生态体验园推出了甲、乙两种消费卡.甲、乙两卡所需费用y甲,y乙(单位:元)与入园次数x(单位:次)的函数关系如图所示.当x满足 时,y甲>y乙.
9.甲骑电动车从A地以匀速前往B地,到达B地后停止,在甲车出发的同时乙骑助力车从B地匀速前往A地,到达A地后停止,甲的速度比乙快.两人之间的距离y(千米)与甲出发的时间x(分钟)的函数关系如图所示,根据图象得出下列信息:
①A,B两地相距15千米;
②甲从A地到B地用了45分钟;
③甲到达B地时,乙离A地还有4千米;
④甲骑电动车的速度为25千米/时.
其中正确的是 .(写出所有正确的序号)
10.A、B两地相距480千米,甲车从A地匀速前往B地,乙车同时从B地沿同一公路匀速前往A地.甲车出发30分钟时发现自己有物件落在A地,于是立即掉头以原速返回取件,取件后立即掉头以原速继续匀速前行(掉头和取件时间忽略不计),两车之间相距的路程y(km)与甲车出发时间t(h)之间的函数关系如图所示.则当甲车到达B地时,乙车离A地的路程为 千米.
11.小明和小杰在同一直道的A,B两点间作匀速往返走锻炼(忽略掉头等时间).小明从A地出发,同时小杰从B地出发,两人第一次相遇时小明曾停下接电话数分钟.图中的折线表示从开始到小杰第一次到达A地止,两人之间的距离y(米)与行走时间x(分)的函数关系图象.则图中的b= 米,d= 分.
12.甲、乙两车沿同一平直公路由A地匀速行驶(中途不停留),前往终点B地,甲、乙两车之间的距离S(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.下列说法其中正确的结论有 .
①A、B两地相距210千米;②甲车速度为60千米/小时;③乙车速度为120千米/小时;④乙车共行驶小时.
13.在一条笔直的公路上有A,B,C三地,其中C地位于A,B两地之间.甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.根据图象可得A,B两地之间的距离为 km;当甲车出发 h时,两车相距300km.
14.甲、乙两车分别从A,B两地同时相向匀速行驶,当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过12小时后两车同时到达距A地300千米的C地(中途休息时间忽略不计).设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则当甲车到达B地时,乙车距A地 千米.
15.甲、乙两小朋友都从A地出发,匀速步行到B地(A、B两地之间为笔直的道路),甲出发半分钟后,乙才从A地出发,经过一段时间追上甲,两人继续向B地步行,当甲、乙之间的距离刚好是70米时,乙立刻掉头以原速度向A地步行,半分钟后与甲相遇,乙又立刻掉头向B地以原速度步行(两次掉头时间忽略不计).甲、乙相距的路程为y(米)与乙出发的时间x(分钟)之间的关系如图所示,当乙到达B地时,甲与B地相距的路程是 米.
16.甲、乙两人在同一条直线跑道AB上进行往返跑,甲从A地出发,乙从A、B之间的C地出发,且比甲晚出发1分钟,甲到达B地后,立即调头返回A地,并将速度降为原速的,而乙到达B地后仍以原速返回A地(甲、乙掉头的时间均忽略不计),两人之间的距离y(米)与甲的时间x(分)之间的部分函数关系如图所示,则当乙到达B地时,甲离A地的距离为 米.
三.解答题
17.小明与小亮进行百米赛跑,小明比小亮跑得快,如果两人同时起跑,小明肯定赢.现在小明让小亮先跑若干米,图中l1,l2分别表示两人在赛跑中的路程与时间的关系(图象不完整).试观察图象并回答下列问题:
(1)哪条线段是表示小明所跑的路程与时间的关系?
(2)小明让小亮先跑了多少米?
(3)谁会赢得这场比赛?
18.某商店销售一种商品,经市场调查发现:当该商品每件售价是50元时,可以销售100件,且利润为1000元;当该商品每件售价是60元时,可以销售80件,且利润为1600元.
(1)该商品每件进价是多少元?
(2)当用字母x表示商品每件售价,用字母y表示商品的销售量时,发现本题中x、y的值总是满足关系式:y=kx+b,请同学们根据题目提供的数据求出k、b的值,并求出当商品每件售价为70元时,销售利润是多少元?
19.抗击疫情,我们在行动.某药店销售A型和B型两种型号的口罩,销售一箱A型口罩可获利120元,销售一箱B型口罩可获利140元.该药店计划一次购进两种型号的口罩共100箱,其中B型口罩的进货量不超过A型口罩的3倍.设购进A型口罩x箱,这100箱口罩的销售总利润为y元.
(1)求y与x的函数关系式;
(2)该商店购进A型、B型口罩各多少箱,才能使销售利润最大?最大利润是多少?
(3)若限定该药店最多购进A型口罩60箱,则这100口罩的销售总利润能否为12540元?请说明理由.
20.如图,在平面直角坐标系中,过点C(0,12)的直线AC与直线OA相交于点A(8,4).
(1)求直线AC的表达式;
(2)求△OAC的面积;
(3)动点M在线段OA和射线AC上运动,是否存在点M,使△OMC的面积是△OAC的面积的?若存在,求出此时点M的坐标;若不存在,请说明理由.
21.如图,平面直角坐标系中,直线y=kx+b经过点A(2,0),D(0,1),点B是第一象限的点且,过点B作BC⊥y轴,垂足为C,CB=1.
(1)直线y=kx+b的解析式;
(2)求点B坐标;
(3)若点M是直线AD上的一个动点,在x轴上存在另一个点N,且以O、B、M、N为顶点的四边形是平行四边形,请直接写出点N的坐标.
22.如图,直线l:y=x+b过点A(﹣3,0),与y轴交于点B,∠OAB的平分线交y轴于点C,过点C作直线AB的垂线,交x轴于点E,垂足是点D.
(1)求点B和点C的坐标;
(2)求直线DE的函数关系式;
(3)设点P是y轴上一动点,当PA+PD的值最小时,请直接写出点P的坐标.
23.某山区的甲乙两地相距240km,一辆货车从甲地出发匀速开往乙地,货车出发2小时后,一辆小汽车从乙地出发匀速开往甲地,两车同时到达各自的目的地.已知两车行驶的路程之和y(km)与货车行驶的时间x(h)之间的函数关系如图所示.
(1)货车的速度是 km/h,a的值为 ,小汽车行驶了 小时到达甲地;
(2)求小汽车出发后y与x之间的函数关系式,并写出b的值;
(3)当两车相距100km时,求货车行驶的时间.
24.如图,在平面直角坐标系中,直线y=x+5与x轴交于点A,与y轴交于点B,过点B的另一直线交x轴正半轴于C,且△ABC面积为15.
(1)求点C的坐标及直线BC的表达式;
(2)若M为线段BC上一点,且△ABM的面积等于△AOB的面积,求M的坐标;
(3)在(2)的条件下,点E为直线AM上一动点,在x轴上是否存在点D,使以点D、E、B、C为顶点的四边形为平行四边形?若存在,直接写出点D的坐标;若不存在,请说明理由.
25.如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,C,经过点C的直线与x轴交于点B(2,0).
(1)求直线BC的解析式;
(2)点P是线段AC上一动点,若直线BP把△ABC的面积分成1:2的两部分,请求点P的坐标;
(3)若点P是直线AC上一动点,点E是坐标轴上一动点,则是否存在动点P使以点B,C,P,E为顶点的四边形是以BC为一边的平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
26.如图,在直角坐标系中放入一个矩形纸片ABCO,BC=10,将纸片翻折后,点B恰好落在x轴上,记为B',折痕为CE,已知OC:OB'=4:3.
(1)求点B'的坐标;
(2)求折痕CE所在直线的解析式;
(3)若点P是y轴上的一个动点,当△CPE为等腰三角形时,请求出点P的坐标.
答案
一.选择题
C.B.C.A.D.B.D.
二.填空题
8.x>10.
9.①④.
10.80.
11.3600,62.5.
12.①②③.
13.480;.
14.100.
15.40.
16..
三.解答题
17.解:(1)l2表示小明所跑的路程与时间的关系;
(2)观察图象可知,小明让小亮先跑了10米;
(3)由图象可知当小明跑了5秒时,小亮跑了40﹣10=30(米),小明跑了35米,
所以小明的速度为:35÷5=7(米/秒),小亮的速度为:30÷5=6(米/秒);
小明到达终点的时间是100÷7=(秒),小亮到达终点的时间是(100﹣10)÷6=15(秒),
∵<15,
∴小明会赢得这场比赛.
18.解:(1)∵100件商品的利润为1000元,
∴一件商品的利润为1000÷100=10(元),
50﹣10=40(元),
∴该商品每件进价是40元;
(2)把x=50,y=100;x=60,y=80分别代入y=kx+b得:
,解得:,
由题意得:,
解得:40≤x≤100,
∴y=﹣2x+200(40≤x≤100),
当x=70元时,y=﹣2×70+200=60,
销售利润为:(70﹣40)×60=1800(元).
∴,
当商品每件售价为70元时,销售利润是1800元.
19.解:(1)根据题意得,
y=120x+140(100﹣x)=﹣20x+14000,
答:y与x的函数关系式为:y=﹣20x+14000;
(2)根据题意得,100﹣x≤3x,解得x≥25,
∵y=﹣20x+14000,k=﹣20<0;
∴y随x的增大而减小,
∵x为正整数,
∴当x=25时,y取最大值为﹣20×25+14000=13500,则100﹣x=75,
即商店购进A型口罩25箱、B型口罩75箱,才能使销售总利润最大,最大利润为13500元;
(3)根据题意得25≤x≤60,
∵y=﹣20x+14000,k=﹣20<0;
∴y随x的增大而减小,
∵x为正整数,
∴当x=60时,y取最小值为﹣20×60+14000=12800,
∵12800>12540,
∴这100箱口罩的销售总利润不能为12540元.
20.解:(1)设直线AC解析式为y=kx+b,
将C(0,12),A(8,4)代入得:
,解得,
∴直线AC解析式为y=﹣x+12;
(2)过A作AH⊥OC于H,如图:
∵A(8,4),AH⊥OC,
∴AH=8,
∵C(0,12),
∴OC=12,
∴S△OAC=OC AH=×12×8=48;
(3)存在,
①若M在线段OA上时,如图:
∵△OMC的面积是△OAC的面积的,
∴M为OA中点,
而A(8,4),
∴M(4,2),
②当M在射线AC上时,如图:
∵△OMC的面积是△OAC的面积的,
∴M为AC的中点,
而A(8,4),C(0,12),
∴M(4,8),
由等底同高的三角形面积相等可知,若M在C上方的射线AC上的M'处,CM'=CM时,△OM'C的面积也等于△OAC的面积的,
此时C为线段MM'的中点,
而C(0,12),M(4,8),
∴M'(﹣4,16),
综上所述,M的坐标为:(4,2)或(4,8)或(﹣4,16).
21.解:(1)∵A(2,0),D(0,1),
将点A、D的坐标代入y=kx+b得:
,
解得:,
∴直线y=kx+b的解析式:y=﹣x+1;
(2)∵BC=1,BC⊥y轴,
∴设B(1,m),
∵AB=,
∴1+m2=5,
解得m=2(负值舍去),
∴B(1,2);
(3)∵点N在x轴上,O、B、M、N为顶点的四边形是平行四边形,
∴BM∥x轴,且BM=ON,
根据(1),点B的坐标为(1,2),
∴﹣x+1=2,
解得x=﹣2,
∴点M的坐标为(﹣2,2),
∴BM=1﹣(﹣2)=1+2=3,
①点N在点O的左边时,ON=BM=3,
∴点N的坐标为(﹣3,0),
②点N在点O的右边时,ON=BM=3,
∴点N的坐标为(3,0),
③作N(﹣3,0)关于A对称的点N′,则N′也符合,
点N′的坐标是(7,0),
综上所述,点N的坐标为(﹣3,0)或(3,0)或(7,0).
22.解:(1)把点A(﹣3,0)代入y=x+b,得b=4,
∴B(0,4),
∴OB=4,
∵A(﹣3,0),
∴OA=3,
在 Rt△AOB中,∠AOB=90°,
∴AB==5.
∵AC平分∠OAB,CD⊥AB,CO⊥OA,
∴CD=CO,∠ACD=∠ACO,
∵AC=AC,
∴△ACD≌△ACO(SAS),
∴AD=AO=3,BD=AB﹣AD=2.
设CD=CO=m,则BC=4﹣m,
在Rt△BDC中,
由勾股定理知,CD2+BD2=BC2,
∴m2+22=(4﹣m)2,
解得,m=,
∴C(0,);
(2)∵CD⊥AB,CO⊥OA,
∴∠CDB=∠COE=90°,
∵CD=CO,∠BCD=∠ECO,
∴△BCD≌△ECO(ASA),
OE=BD=2,
∴E的坐标(2,0),
∵C(0,),
设直线DE的函数关系式为y=kx+,
∴0=2k+,解得:k=﹣,
∴直线DE的函数关系式为y=﹣x+;
(3)作点A关于y轴对称的点A′,连接A′D交y轴于点P,即为所求的点P,此时,PA+PD的值最小,过点D作DF⊥BC于F,
∵CD=CO=,OB=4,
∴BC=,
∵CD⊥AB,BD=2,
∴DF==,
∵直线DE的函数关系式为y=﹣x+,
∴D(﹣,),
∵A(﹣3,0),
∴A′(3,0),
设A′D的解析式为y=k′x+b′,
∴,解得:,
∴A′D的解析式为y=﹣x+,
当x=0时,y=,
∴点P的坐标为(0,).
23.解:(1)由图象可得,
货车的速度是80÷2=40(km/h),
a=240+240=480,
6﹣2=4(小时),
小汽车行驶了4小时到达甲地,
故答案为:40,480,4;
(2)设小汽车出发后y与x之间的函数关系式为y=kx+m,
由题意得:,
解得,
即小汽车出发后y与x之间的函数关系式为y=100x﹣120,
∴当x=3时,y=100×3﹣120=180,
∴b的值为180;
(3)当两车相遇前相距100km时,
y+100=240,
即100x﹣120+100=240,
解得,
当两车相遇后相距100km时,
y﹣100=240,
即100x﹣120﹣100=240,
解得,
24.解:(1)直线y=x+5与x轴交于点A,与y轴交于点B,
∴A(﹣2,0),B(0,5),
即OA=2,OB=5,
∵△ABC面积为15,
∴(OA+OC) OB=15,
∴OC=4,
∴C(4,0),
设直线BC的表达式为y=kx+b,
将点B、C的坐标代入一次函数表达式得:,
解得:,
∴直线BC的表达式为:y=﹣x+5;
(2)∵S△ACM=S△ABC﹣S△ABM=S△ABC﹣S△ABO=15﹣×2×5=10,
∴S△ACM=×6×ym=10,解得:ym=,
解得:xm=,
∴M(,);
(3)∵A(﹣2,0),M(,),
设直线AM的表达式为y=k′x+b′,
将点A、M的坐标代入一次函数表达式得:,
解得:,
∴直线AM的表达式为:y=x+2.
①当BC为平行四边形的边,四边形BCDE为平行四边形时,如图:
∵B(0,5),BE∥CD,BE=CD,
∴点E的纵坐标是5,
∵点E为直线AM上一动点,直线AM的表达式为:y=x+2.
∴x+2=5,解得:x=3,
∴E (3,5),
∴BE=CD=3,
∵C(4,0),
∴D(7,0);
②当BC为平行四边形的边,四边形BDEC为平行四边形时,如图:过点E作EF⊥x轴于F,
∵四边形BDEC为平行四边形,
∴BC=ED,∠DBC=∠CED,BD=EC,
∴△BDC≌△ECD(SAS),
∴EF=OB,
∵B(0,5),
∴EF=OB=5,
∴点E的纵坐标是﹣5,
∵点E为直线AM上一动点,直线AM的表达式为:y=x+2.
∴x+2=﹣5,解得:x=﹣7,
∴OF=7,
在Rt△BOC和Rt△EFD中,
,
∴Rt△BOC≌Rt△EFD(HL),
∴DF=OC,
∵C(4,0),
∴DF=4,
∴OD=4+7=11,
∴D(﹣11,0);
③当BC为平行四边形的对角线时,
∵B(0,5),BE∥CD,BE=CD,
∴点E的纵坐标是5,
∵点E为直线AM上一动点,直线AM的表达式为:y=x+2.
∴x+2=5,解得:x=3,
∴E (3,5),
∴BE=CD=3,
∵C(4,0),
∴D(1,0).
综上,存在,满足条件的点D的坐标为(7,0)或(﹣11,0)或(1,0).
25.解:(1)由得:A(﹣4,0),C(0,﹣2),
设直线BC的解析式为y=kx+b(k≠0):
∴,解得:,
∴直线BC的解析式为y=;
(2)∵A(﹣4,0),C(0,﹣2),B(2,0).
∴AC=6,
∴S△ABC=×6×2=6,
设P(m,),(﹣4<m<0),
①当S△ABP:S△BPC=1:2时,即=,
∴,
∴m=,
∴;
当S△ABP:S△BPC=2:1时,即=,
∴,
∴m=,
∴,
∴;
(3)以点B,C,P,E为顶点的四边形是以BC为一边的平行四边形,
设P(m,)(﹣4<m<0),
①如图,当E在y轴的正半轴上时,C也在y轴上,设对角线PB、CE的交点为Q,则点Q在y轴上,
∵四边形PEBC是平行四边形,
∴PQ=BQ,
∵B(2,0),(m+2)=0,
∴m=﹣2,
代入P(m,)得=﹣,
∴P1(﹣2,﹣);
②如图,当E在y轴的负半轴上时,BP=CE.BP∥y轴,
∵B(2,0),
∴m=2,=﹣3,
∴P2(2,﹣3);
③如图,当E在x轴的负半轴上,EB为对角线,PA=CA.
∵A(﹣4.0),P(m,),C(0.﹣2),
∴(m+0)=﹣4,
解得:m=﹣8,
∴=2,
∴P3(﹣8,2).
综上,存在,P1(﹣2,﹣),P2(2,﹣3),P3(﹣8,2).
26.解:(1)∵四边形OABC是矩形,
∴∠AOC=90°,
∵OC:OB'=4:3,
设OC=4x,则OB'=3x,
∴B'C==5x,
∵B'C=BC=10,
即5x=10,
解得x=2,
∴OB'=3x=6,
∴B'(6,0);
(2)由(1)知,OC=4x=8,
∴C(0,8),
设AE=a,则BE=B'E=8﹣a,AB'=AO﹣OB'=10﹣6=4,
由勾股定理,得AE2+AB'2=BE'2,
即a2+42=(8﹣a)2,
解得a=3,
∴E点坐标为(10,3),
设直线CE的解析式为y=kx+b,
代入C点和E点坐标,得,
解得,
∴CE所在的直线解析式为y=﹣x+8;
(3)由(2)知,C(0,8),E(10,3),
设P(0,t),
则CE==5,CP=|8﹣t|,EP=,
若△CPE为等腰三角形,分以下三种情况:
①当CP=CE时,
即|8﹣t|=5,
∴t=8+5或8﹣5,
故P点坐标为(8+5,0)或(8﹣5,0);
②当CE=EP时,
即5=,
解得t=﹣2或8,
故P点的坐标为(﹣2,0)或(8,0),
③当CP=EP时,
即|8﹣t|=,
解得t=﹣,
故P点的坐标为(﹣,0);
综上,当△CPE为等腰三角形时,P点的坐标为(8+5,0)或(8﹣5,0)或(﹣2,0)或(8,0)或(﹣,0).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
