北师大版八年级数学上册试题 第5章 二元一次方程组测试卷(含答案)
文档属性
| 名称 | 北师大版八年级数学上册试题 第5章 二元一次方程组测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 253.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 00:00:00 | ||
图片预览




文档简介
第5章 二元一次方程组测试卷
一、选择题(本大题共12小题,每小题3分,共36分)
1.如图所示,若一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组的解是( )
A. B. C. D.
2.若最简二次根式和能合并,则a、b的值分别是( )
A.2和1 B.1和2 C.2和2 D.1和1
3.下列方程中,①x+y=6;②x(x+y)=2;③3x-y=z+1;④m+=7是二元一次方程的有( )
A.1个 B.2个 C.3个 D.4个
4.已知一次函数,过点,那么这个函数的表达式为( )
A. B. C. D.
5.如图,直线与相交于点,则关于x的方程的解是( )
A. B. C. D.
6.关于的二元一次方程组的解满足,则k的值是( )
A.2 B. C. D.3
7.如图,用12块形状和大小均相同的小长方形纸片拼成一个宽是60厘米的大长方形,则每个小长方形的周长是( )
A.60厘米 B.80厘米 C.100厘米 D.120厘米
8.若,则的负倒数是( )
A.2 B.-2 C. D.
9.由方程组可以得出关于x和y的关系式是( )
A. B. C. D.
10.关于x,y的方程是二元一次方程,则m和n的值是( )
A. B. C. D.
11.某车间有2个小组,甲组是乙组人数的2倍,若从甲组调8人到乙组,那么甲组人数比乙组人数的一半还多6人,则原来乙组的人数为( )
A.6 B.8 C.10 D.12
12.在平面直角坐标系中,已知A、B、C三点的坐标分别为(8,0)、(9,6)、(0,6),若一次函数y=kx﹣8k的图象将△ABC分成面积为1∶2的两个部分,则k的值为( )
A.﹣3 B.﹣2 C.﹣3或 D.﹣2或﹣3
二、填空题(本大题共6小题,每小题3分,共18分)
13.方程组有正整数解,则正整数a的值为________.
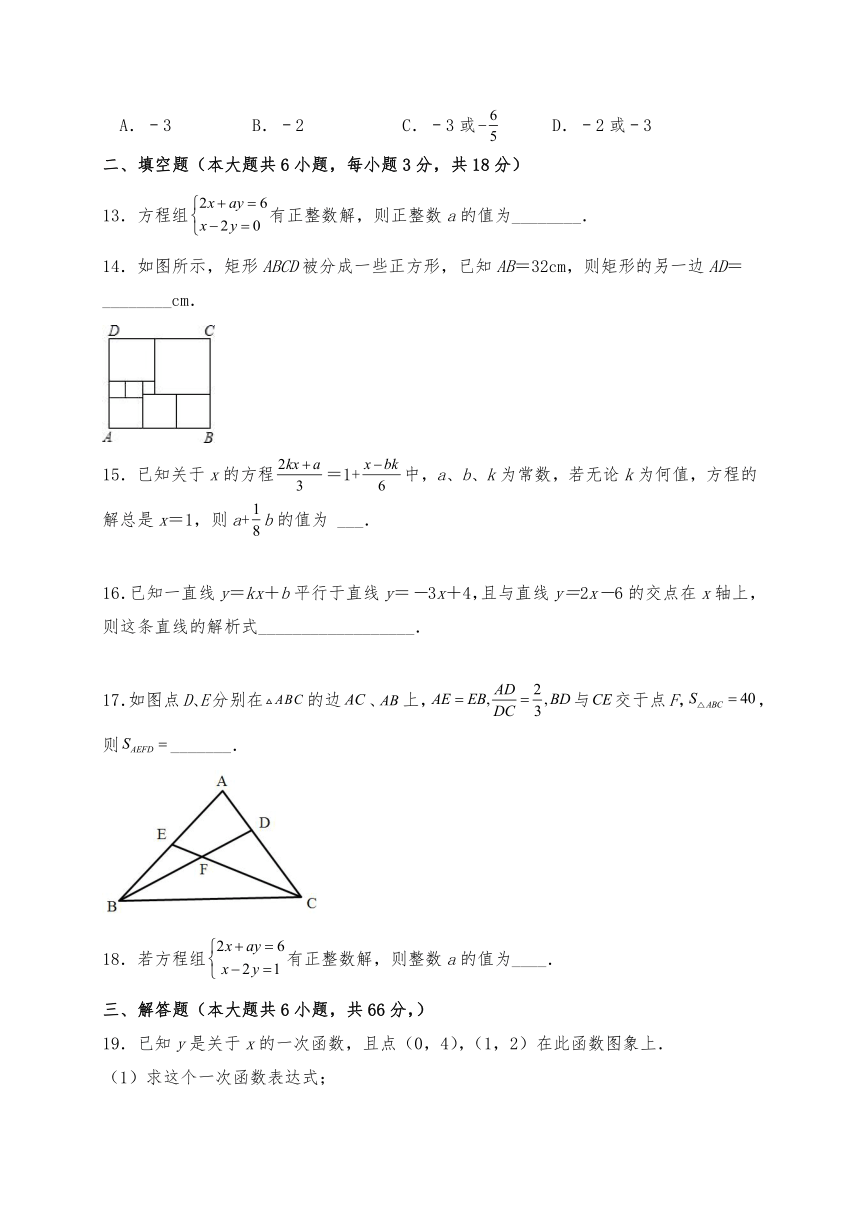
14.如图所示,矩形ABCD被分成一些正方形,已知AB=32cm,则矩形的另一边AD=________cm.
15.已知关于x的方程=1+中,a、b、k为常数,若无论k为何值,方程的解总是x=1,则a+b的值为 ___.
16.已知一直线y=kx+b平行于直线y=-3x+4,且与直线y=2x-6的交点在x轴上,则这条直线的解析式__________________.
17.如图点D、E分别在的边、上,与交于点F,,则_______.
18.若方程组有正整数解,则整数a的值为____.
三、解答题(本大题共6小题,共66分,)
19.已知y是关于x的一次函数,且点(0,4),(1,2)在此函数图象上.
(1)求这个一次函数表达式;
(2)求当时x的取值范围;
(3)在函数图象上有点P,点P到y轴的距离为2,直接写出P点的坐标.
20.已知一次函数的图象过点(-1,5),且与正比例函数y=-x的图象交于点(2,a).求:
(1)一次函数表达式;
(2)这两个函数图象与x轴所围成的三角形面积.
21.如图,一次函数y=kx+b(k≠0)的图象经过点A、B.
(1)根据图象,求一次函数y=kx+b(k≠0)的表达式;
(2)将直线AB向下平移5个单位后经过点(m,﹣5),求m的值.
22.解方程组
(1) (2)
23.已知一次函数y1=mx﹣2m+4(m≠0).
(1)判断点(2,4)是否在该一次函数的图象上,并说明理由;
(2)若一次函数y2=﹣x+6,当m>0,试比较函数值y1与y2的大小;
(3)函数y1随x的增大而减小,且与y轴交于点A,若点A到坐标原点的距离小于6,点B,C的坐标分别为(0,﹣2),(2,1).求△ABC面积的取值范围.
24.已知函数y=kx+b(k≠0)的图象经过点A(﹣2,1),点 B(1,).
(1)求直线AB的解析式;
(2)若在x轴上存在点C,使S△ACO=S△ABO,求出点C坐标.
答案
一、选择题
A.D.A.A.B.B.D.D.C.C.D.C.
二、填空题
13.2
14.29
15.
16.y=-3x+9
17.11
18.-3或-1或±2
三、解答题
19.
(1)设,把点(0,4),(1,2)代入得:
解得:,
即
(2)当时,
当时,;
当时,.
,
y随x的增大而减小.
∴x的范围是.
(3)∵点P到y轴的距离为2,
∴点P的横坐标为2或者-2
∵P点在上
∴P点坐标为(2,0),
20.
(1)解:设一次函数表达式为:,
正比例函数y=-x的图象经过点(2,a),
即该点坐标为(2,-1),
由题意可知:一次函数的图象过点(-1,5)和(2,-1),
,解得,
一次函数表达式为.
(2)解:如图所示,设两个函数图像的交点为P,即P点坐标为(2,-1),一次函数与x轴的交点为A,
A点是一次函数与x轴的交点坐标,
,解得 ,即A点坐标为(,),
,
P点坐标为(2,-1),
点P到x轴的距离为1,
两个函数图象与x轴所围成的三角形面积为:.
21.
解:(1)由图象可知,一次函数y=kx+b(k≠0)的图象经过点A(2,6)、B(﹣4,﹣3),
∴,
解得,
所以一次函数的表达式为:;
(2)将直线AB向下平移5个单位后得到,即,
∵经过点(m,﹣5),
∴,
解得m=﹣2.
22.
解:(1)
①-②得:
解得:
把代入②得:
所以方程组的解为:;
(2)
由②得:③
①-③得:
解得:④
把④代入①得:⑤
④+⑤得:
把代入④得:
所以方程组的解为:
23.
解:(1)把x=2代入y1=mx﹣2m+4得,y1=2m﹣2m+4=4,
∴点(2,4)在该一次函数的图象上;
(2)∵一次函数y2=﹣x+6的图象经过点(2,4),点(2,4)在一次函数y1=mx﹣2m+4的图象上,
∴一次函数y2=﹣x+6的图象与函数y1=mx﹣2m+4的图象的交点为(2,4),
∵y2随x的增大而减小,y1随x的增大而增大,
∴当x>2时,y1>y2;
当x=2时,y1=y2;
当x<2时,y1<y2;
(3)由题意可知,﹣6<﹣2m+4<6且m<0,
∴﹣1<m<0,
∵点B,C的坐标分别为(0,﹣2),(2,1).
∴6<AB<8,
∴6<S△ABC<8.
24.
(1)∵一次函数y=kx+b的图象经过点A(-2,1)、点B(1, ).
∴,
∴,
∴一次函数的解析式为;
(2)如图所示,过点A作AD⊥x轴于D,过点B作BE⊥x轴于E,
∵A(-2,1)、点B(1, ),
∴,,,,
∴,
∴
,
∴
∴,
∴点C的坐标为(3,0)或(-3,0).
一、选择题(本大题共12小题,每小题3分,共36分)
1.如图所示,若一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组的解是( )
A. B. C. D.
2.若最简二次根式和能合并,则a、b的值分别是( )
A.2和1 B.1和2 C.2和2 D.1和1
3.下列方程中,①x+y=6;②x(x+y)=2;③3x-y=z+1;④m+=7是二元一次方程的有( )
A.1个 B.2个 C.3个 D.4个
4.已知一次函数,过点,那么这个函数的表达式为( )
A. B. C. D.
5.如图,直线与相交于点,则关于x的方程的解是( )
A. B. C. D.
6.关于的二元一次方程组的解满足,则k的值是( )
A.2 B. C. D.3
7.如图,用12块形状和大小均相同的小长方形纸片拼成一个宽是60厘米的大长方形,则每个小长方形的周长是( )
A.60厘米 B.80厘米 C.100厘米 D.120厘米
8.若,则的负倒数是( )
A.2 B.-2 C. D.
9.由方程组可以得出关于x和y的关系式是( )
A. B. C. D.
10.关于x,y的方程是二元一次方程,则m和n的值是( )
A. B. C. D.
11.某车间有2个小组,甲组是乙组人数的2倍,若从甲组调8人到乙组,那么甲组人数比乙组人数的一半还多6人,则原来乙组的人数为( )
A.6 B.8 C.10 D.12
12.在平面直角坐标系中,已知A、B、C三点的坐标分别为(8,0)、(9,6)、(0,6),若一次函数y=kx﹣8k的图象将△ABC分成面积为1∶2的两个部分,则k的值为( )
A.﹣3 B.﹣2 C.﹣3或 D.﹣2或﹣3
二、填空题(本大题共6小题,每小题3分,共18分)
13.方程组有正整数解,则正整数a的值为________.
14.如图所示,矩形ABCD被分成一些正方形,已知AB=32cm,则矩形的另一边AD=________cm.
15.已知关于x的方程=1+中,a、b、k为常数,若无论k为何值,方程的解总是x=1,则a+b的值为 ___.
16.已知一直线y=kx+b平行于直线y=-3x+4,且与直线y=2x-6的交点在x轴上,则这条直线的解析式__________________.
17.如图点D、E分别在的边、上,与交于点F,,则_______.
18.若方程组有正整数解,则整数a的值为____.
三、解答题(本大题共6小题,共66分,)
19.已知y是关于x的一次函数,且点(0,4),(1,2)在此函数图象上.
(1)求这个一次函数表达式;
(2)求当时x的取值范围;
(3)在函数图象上有点P,点P到y轴的距离为2,直接写出P点的坐标.
20.已知一次函数的图象过点(-1,5),且与正比例函数y=-x的图象交于点(2,a).求:
(1)一次函数表达式;
(2)这两个函数图象与x轴所围成的三角形面积.
21.如图,一次函数y=kx+b(k≠0)的图象经过点A、B.
(1)根据图象,求一次函数y=kx+b(k≠0)的表达式;
(2)将直线AB向下平移5个单位后经过点(m,﹣5),求m的值.
22.解方程组
(1) (2)
23.已知一次函数y1=mx﹣2m+4(m≠0).
(1)判断点(2,4)是否在该一次函数的图象上,并说明理由;
(2)若一次函数y2=﹣x+6,当m>0,试比较函数值y1与y2的大小;
(3)函数y1随x的增大而减小,且与y轴交于点A,若点A到坐标原点的距离小于6,点B,C的坐标分别为(0,﹣2),(2,1).求△ABC面积的取值范围.
24.已知函数y=kx+b(k≠0)的图象经过点A(﹣2,1),点 B(1,).
(1)求直线AB的解析式;
(2)若在x轴上存在点C,使S△ACO=S△ABO,求出点C坐标.
答案
一、选择题
A.D.A.A.B.B.D.D.C.C.D.C.
二、填空题
13.2
14.29
15.
16.y=-3x+9
17.11
18.-3或-1或±2
三、解答题
19.
(1)设,把点(0,4),(1,2)代入得:
解得:,
即
(2)当时,
当时,;
当时,.
,
y随x的增大而减小.
∴x的范围是.
(3)∵点P到y轴的距离为2,
∴点P的横坐标为2或者-2
∵P点在上
∴P点坐标为(2,0),
20.
(1)解:设一次函数表达式为:,
正比例函数y=-x的图象经过点(2,a),
即该点坐标为(2,-1),
由题意可知:一次函数的图象过点(-1,5)和(2,-1),
,解得,
一次函数表达式为.
(2)解:如图所示,设两个函数图像的交点为P,即P点坐标为(2,-1),一次函数与x轴的交点为A,
A点是一次函数与x轴的交点坐标,
,解得 ,即A点坐标为(,),
,
P点坐标为(2,-1),
点P到x轴的距离为1,
两个函数图象与x轴所围成的三角形面积为:.
21.
解:(1)由图象可知,一次函数y=kx+b(k≠0)的图象经过点A(2,6)、B(﹣4,﹣3),
∴,
解得,
所以一次函数的表达式为:;
(2)将直线AB向下平移5个单位后得到,即,
∵经过点(m,﹣5),
∴,
解得m=﹣2.
22.
解:(1)
①-②得:
解得:
把代入②得:
所以方程组的解为:;
(2)
由②得:③
①-③得:
解得:④
把④代入①得:⑤
④+⑤得:
把代入④得:
所以方程组的解为:
23.
解:(1)把x=2代入y1=mx﹣2m+4得,y1=2m﹣2m+4=4,
∴点(2,4)在该一次函数的图象上;
(2)∵一次函数y2=﹣x+6的图象经过点(2,4),点(2,4)在一次函数y1=mx﹣2m+4的图象上,
∴一次函数y2=﹣x+6的图象与函数y1=mx﹣2m+4的图象的交点为(2,4),
∵y2随x的增大而减小,y1随x的增大而增大,
∴当x>2时,y1>y2;
当x=2时,y1=y2;
当x<2时,y1<y2;
(3)由题意可知,﹣6<﹣2m+4<6且m<0,
∴﹣1<m<0,
∵点B,C的坐标分别为(0,﹣2),(2,1).
∴6<AB<8,
∴6<S△ABC<8.
24.
(1)∵一次函数y=kx+b的图象经过点A(-2,1)、点B(1, ).
∴,
∴,
∴一次函数的解析式为;
(2)如图所示,过点A作AD⊥x轴于D,过点B作BE⊥x轴于E,
∵A(-2,1)、点B(1, ),
∴,,,,
∴,
∴
,
∴
∴,
∴点C的坐标为(3,0)或(-3,0).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
