北师大版八年级数学上册试题 第七章 平行线的证明单元检测卷 (含答案)
文档属性
| 名称 | 北师大版八年级数学上册试题 第七章 平行线的证明单元检测卷 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 988.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 13:57:18 | ||
图片预览




文档简介
第七章 平行线的证明单元检测卷
一、选择题(本大题共12小题,每小题3分,共36分).
1.下列语句是命题的是( )
A.同旁内角相等,两直线平行 B.等于同一个角的两个角相等吗?
C.延长线段AB到点C,使 D.连接A,B两点
2.下列真命题的个数是 ( )
(1)直线a、b、c、d,如果a∥b、c∥b、c∥d,则a∥d.
(2)两条直线被第三条直线所截,同旁内角的平分线互相垂直.
(3)两条直线被第三条直线所截,同位角相等.
(4)在同一平面内,如果两直线都垂直于同一条直线,那么这两直线平行.
A.1个 B.2个 C.3个 D.4个
3.已知直线m∥n,将一块含30°角的直角三角板按如图所示方式放置(∠ABC=30°),并且顶点A,C分别落在直线m,n上,若∠1=38°,则∠2的度数是( )
A.20° B.22° C.28° D.38°
4.如图,AB⊥AF,∠B、∠C、∠D、∠E、∠F的关系为( )
A.∠B+∠C+∠D+∠E+∠F=270° B.∠B+∠C﹣∠D+∠E+∠F=270°
C.∠B+∠C+∠D+∠E+∠F=360° D.∠B+∠C﹣∠D+∠E+∠F=360°
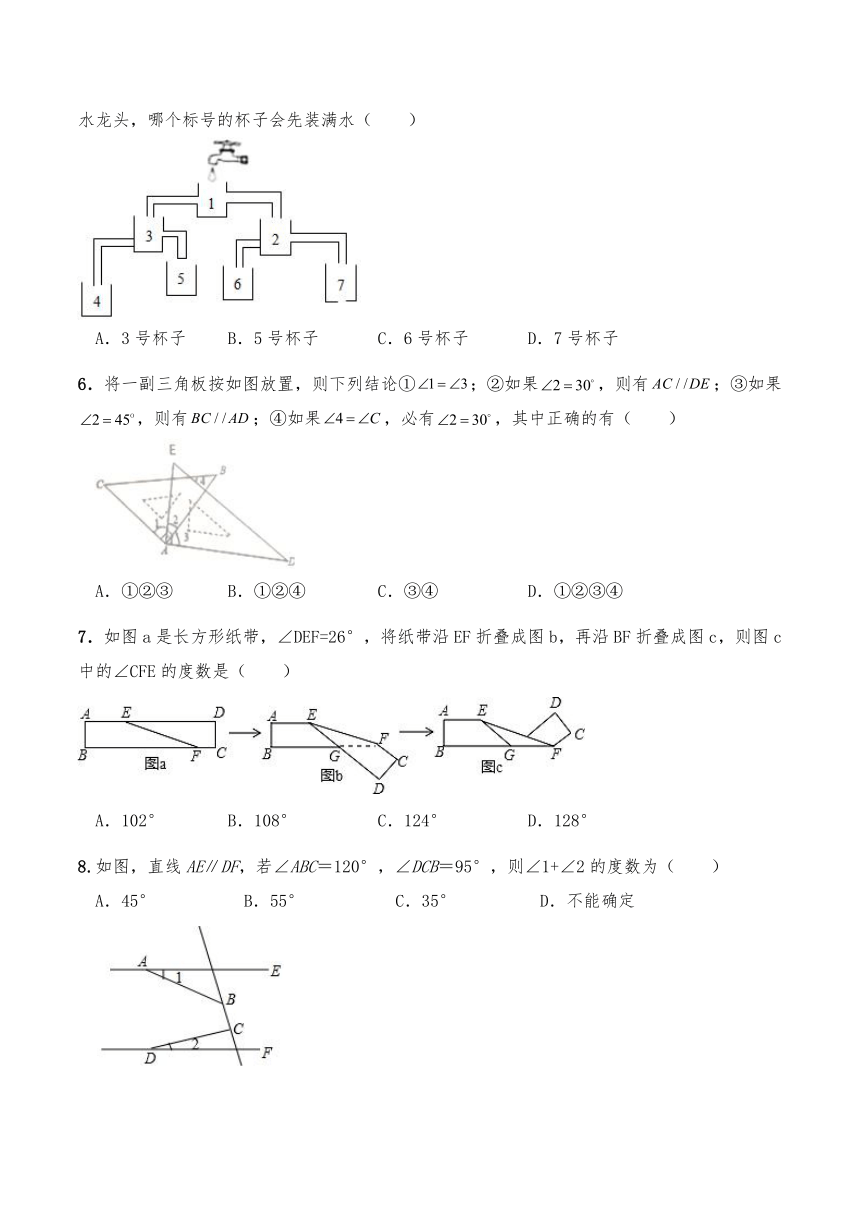
5.最近网上一个烧脑问题的关注度很高(如图所示),通过仔细观察、分析图形,你认为打开水龙头,哪个标号的杯子会先装满水( )
A.3号杯子 B.5号杯子 C.6号杯子 D.7号杯子
6.将一副三角板按如图放置,则下列结论①;②如果,则有;③如果,则有;④如果,必有,其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
7.如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
A.102° B.108° C.124° D.128°
8.如图,直线AE∥DF,若∠ABC=120°,∠DCB=95°,则∠1+∠2的度数为( )
A.45° B.55° C.35° D.不能确定
9.如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:① BC平分∠ABE;② AC∥BE;③ ∠CBE+∠D=90°;④ ∠DEB=2∠ABC.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
10.如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若∠AOB=40°,则∠MPN的度数是( )
A.90° B.100° C.120° D.140°
11.如图,,M,N分别是边上的定点,P,Q分别是边上的动点,记,当的值最小时,关于,的数量关系正确的是( )
A. B. C. D.
12.如图,,、、分别平分的外角、内角、外角.以下结论:①:②;③;④平分;⑤.其中错误的结论有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(本大题共6小题,每小题3分,共18分)
13.甲和乙玩一个猜数游戏,规则如下:已知五张纸牌上分别写有1、2、3、4、5五个数字,现甲、乙两人分别从中各自随机抽取一张,然后根据自己手中的数推测谁手上的数更大.甲看了看自己手中的数,想了想说:我不知道谁手中的数更大;乙听了甲的判断后,思索了一下说:我也不知道谁手中的数更大.假设甲、乙所作出的推理都是正确的,那么乙手中的数是____.
14.已知Rt△ABC中,∠C=90°,将∠C沿DE向三角形内折叠,使点C落在△ABC的内部,如图,则∠1+∠2=___度.
15.如图,在中,,与的平分线交于点,得;与的平分线相交于点,得;;与的平分线相交于点,得,则______.
16.如图,将一副三角板按如图所示放置,,,,且,则下列结论中:①;②若平分,则有;③将三角形绕点旋转,使得点落在线段上,则此时;④若,则.其中结论正确的选项有______.(写出所有正确结论的序号)
17.如图,在平面直角坐标系中,为坐标原点,点的坐标为,点的坐标为,点是直线:上的一个动点,若,则点的坐标是__________.
18.如图,在中,和的平分线、相交于点,交于点,交 于点,过点作于点,则下列三个结论:①;②当时,;③若,,则.其中正确的是______.
三、解答题(本大题共8小题,共66分.)
19.(1)学行线以后,香橙同学想出了过一点画一条直线的平行线的新方法,她是通过折纸做的,过程如(图1).
①请你仿照以上过程,在图2中画出一条直线b,使直线b经过点P,且,要求保留折纸痕迹,画出所用到的直线,指明结果.无需写画法:
②在(1)中的步骤(b)中,折纸实际上是在寻找过点P的直线a的 线.
(2)已知,如图3,,BE平分,CF平分.求证:(写出每步的依据).
20.如图所示,点B,E,C,F在同一条直线上,能否由,来证明AC∥DE?如果能,请给出证明;如果不能,请从下列四个条件中再选择一个合适的条件,使AC∥DE成立,并说明理由.供选择的四个条件:①;②;③AB∥DF;④.
21.已知:如图,点E在线段CD上,EA、EB分别平分∠DAB和∠ABC,∠AEB=90°,设AD=x,BC=y,且(x﹣2)2+|y﹣5|=0.
(1)求AD和BC的长.(2)试说线段AD与BC有怎样的位置关系?并证明你的结论.
(3)你能求出AB的长吗?若能,请写出推理过程,若不能,说明理由.
22.如图1,已知线段AB、CD相交于点O,连接AC、BD.(1)求证:∠A+∠C=∠B+∠D;(2)如图2,∠CAB与∠BD的平分线AP、DP相交于点P,求证:∠B+∠C=2∠P.
23.如图,直线AB∥直线CD,线段EF∥CD,连接BF、CF.
(1)求证:∠ABF+∠DCF=∠BFC;(2)连接BE、CE、BC,若BE平分∠ABC,BE⊥CE,求证:CE平分∠BCD;(3)在(2)的条件下,G为EF上一点,连接BG,若∠BFC=∠BCF,∠FBG=2∠ECF,∠CBG=70°,求∠FBE的度数.
24.综合与探究:小新在学习过程中,发现课本有一道习题,他在思考过程中,对习题做了一定变式,让我们来一起看一下吧.在中,与的平分线相交于点.
(1)如图,如果,求的度数.
(2)在()的条件下,如图2,作的外角,的平分线交于点,求的度数.
(3)如图,作的外角,的平分线交于点,延长线段,交于点,在中,是否存在一个内角等于另一个内角的倍,若存在,请直接写出的度数;若不存在,请说明理由.
25.点E在射线DA上,点F、G为射线BC.上两个动点,满足∠DBF=∠DEF,∠BDG=∠BGD,DG平分∠BDE.(1)如图,当点G在F右侧时,求证:;
(2)如图,当点G在BF左侧时,求证:;(3)如图,在(2)的条件下,P为BD延长线上一点,DM平分∠BDG,交BC于点M,DN平分∠PDM,交EF于点N,连接NG,若DG⊥NG,,求∠B的度数.
26.如图,在平面直角坐标系中,A为轴上的一动点,B(0,3),BAC=,AB=AC.
(1)如图1,若,点C在第二象限,求C点坐标;
(2)如图2,当点C在第四象限时,点F与点B关于轴对称,连接CF并延长交轴于点E,求点E坐标;(3)如图3,P为第二象限的点,点H在线段PF上,且,当点E在轴负半轴上,点F在y轴负半轴上运动时,且OE=OF,求m、n之间的数量关系.
答案
一、选择题
A.B.B.B.A.D.A.C.D.B.B.B.
二、填空题
13.3
14.
15.
16.②③④
17.或
18.①②
三、解答题
19.(1)解:①如图2所示:
②在(1)中的步骤(b)中,折纸实际上是在寻找过点的直线的垂线.故答案为垂;
(2)证明:平分,平分(已知),,(角平分线的定义),
(已知),(两直线平行,内错角相等),
(等量代换),(等式性质),(内错角相等,两直线平行).
20.解:由AC=DE,BE=FC无法证明,
选择条件②AB=DF进行证明,
∵BE=FC,∴BE+CE=FC+CE,∴BC=FE,
在△ABC和△DFE中,,
∴△ABC≌△DFE(SSS),∴∠ACB=∠DFE,∴;
选择条件④ ,
∵,∴三角形ABC和三角形DFE都是直角三角形,
在Rt△ABC和Rt△DFE中,∴Rt△ABC≌Rt△DFE(HL),
∴∠ACB=∠DFE,∴.
21.解:(1),,,解得,,即,;
(2).理由如下:、分别平分和,
,,,
,,,;
(3)能.理由如下:延长交直线于,如图,
,,而,,
在△AEB和△FEB中,
∴△AEB≌△FEB(AAS),AE=EF.
在△ADE和△FCE中,
,,.
22.证明:(1)在△AOC中,∠A+∠C=180°﹣∠AOC,
在△BOD中,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,∴∠A+∠C=∠B+∠D;
(2)在AP、CD相交线中,有∠CAP+∠C=∠P+∠CDP,
在AB、DP相交线中,有∠B+∠BDP=∠P+∠BAP,
∴∠B+∠C+∠CAP+∠BDP=2∠P+∠CDP+∠BAP,
∵AP、DP分别平分∠CAB、∠BDC,∴∠CAP=∠BAP,∠BDP=∠CDP,∴∠B+∠C=2∠P.
23.证明:(1)∵AB∥CD,EF∥CD,∴AB∥EF,∴∠ABF=∠BFE,
∵EF∥CD,∴∠DCF=∠EFC,∴∠BFC=∠BFE+∠EFC=∠ABF+∠DCF;
(2)∵BE⊥EC,∴∠BEC=90°,∴∠EBC+∠BCE=90°,
由(1)可得:∠BFC=∠ABE+∠ECD=90°,∴∠ABE+∠ECD=∠EBC+∠BCE,
∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ECD=∠BCE,∴CE平分∠BCD;
(3)设∠BCE=β,∠ECF=γ,
∵CE平分∠BCD,∴∠DCE=∠BCE=β,
∴∠DCF=∠DCE﹣∠ECF=β﹣γ,∴∠EFC=β﹣γ,
∵∠BFC=∠BCF,∴∠BFC=∠BCE+∠ECF=γ+β,∴∠ABF=∠BFE=2γ,
∵∠FBG=2∠ECF,∴∠FBG=2γ,∴∠ABE+∠DCE=∠BEC=90°,
∴∠ABE=90°﹣β,∴∠GBE=∠ABE﹣∠ABF﹣∠FBG=90°﹣β﹣2γ﹣2γ,
∵BE平分∠ABC,∴∠CBE=∠ABE=90°﹣β,∴∠CBG=∠CBE+∠GBE,
∴70°=90°﹣β+90°﹣β﹣2γ﹣2γ,整理得:2γ+β=55°,
∴∠FBE=∠FBG+∠GBE=2γ+90°﹣β﹣2γ﹣2γ=90°﹣(2γ+β)=35°.
24.解:(1),.
点是和的平分线的交点,.
(2)外角,的角平分线交于点,
∴,
.
(3)存在,的度数为或或 如图,延长至,
∵为的外角的角平分线,∴是的外角的平分线,∴
∵平分,∴
∵,∴,即.
又∵,∴,即.
,
如果在中存在一个内角等于另一个内角的倍,那么分四种情况:
①,则;
②,则,,;
③,则,解得
④,则,解得.
综上所述,的度数是或或
25.解:(1)∵DG平分∠BDE,∴∠BDG=∠ADG,
又∵∠BDG=∠BGD,∴∠ADG=∠DGB,∴,∴∠DEF=∠EFG,
∵∠DBF=∠DEF,∴∠DBF=∠EFG,∴;
(2)过点G作交AD于K,同理可证,
∴,∴∠BDG=∠DGK,∠GEF=∠KGE,
∴∠DGE=∠DGK+∠KGE,∴∠DGE=∠BDG+∠FEG;
(3)设,则,,,∵DN平分∠PDM,∴,
∴,,
∵DG⊥NG,∴,∴,
∵,∴,
∵,∴,∴,∴.
26.(1)过点C作交OA于点D,
∵,∴. , . , .
,.
在和中
, , ;
(2)过点C作交AE于点G,
∵,∴,. , .
,.
在和中
, , .
∵点F与点B关于轴对称, .设直线FC的解析式为,
将,代入解析式中得 解得
∴直线FC的解析式为. 令,则,解得, ∴;
(3),理由如下:设直线OH的解析式为,
,, , ∴直线OH的解析式为.
,. 设直线PF的解析式为 ,
将代入解析式中得 ,∴直线PF的解析式为 .
当时,,, .
,, ,, ,
设直线PE的解析式为, 将代入解析式中得,
∴直线PE的解析式为.
解得点P的纵坐标为,, .
一、选择题(本大题共12小题,每小题3分,共36分).
1.下列语句是命题的是( )
A.同旁内角相等,两直线平行 B.等于同一个角的两个角相等吗?
C.延长线段AB到点C,使 D.连接A,B两点
2.下列真命题的个数是 ( )
(1)直线a、b、c、d,如果a∥b、c∥b、c∥d,则a∥d.
(2)两条直线被第三条直线所截,同旁内角的平分线互相垂直.
(3)两条直线被第三条直线所截,同位角相等.
(4)在同一平面内,如果两直线都垂直于同一条直线,那么这两直线平行.
A.1个 B.2个 C.3个 D.4个
3.已知直线m∥n,将一块含30°角的直角三角板按如图所示方式放置(∠ABC=30°),并且顶点A,C分别落在直线m,n上,若∠1=38°,则∠2的度数是( )
A.20° B.22° C.28° D.38°
4.如图,AB⊥AF,∠B、∠C、∠D、∠E、∠F的关系为( )
A.∠B+∠C+∠D+∠E+∠F=270° B.∠B+∠C﹣∠D+∠E+∠F=270°
C.∠B+∠C+∠D+∠E+∠F=360° D.∠B+∠C﹣∠D+∠E+∠F=360°
5.最近网上一个烧脑问题的关注度很高(如图所示),通过仔细观察、分析图形,你认为打开水龙头,哪个标号的杯子会先装满水( )
A.3号杯子 B.5号杯子 C.6号杯子 D.7号杯子
6.将一副三角板按如图放置,则下列结论①;②如果,则有;③如果,则有;④如果,必有,其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
7.如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
A.102° B.108° C.124° D.128°
8.如图,直线AE∥DF,若∠ABC=120°,∠DCB=95°,则∠1+∠2的度数为( )
A.45° B.55° C.35° D.不能确定
9.如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:① BC平分∠ABE;② AC∥BE;③ ∠CBE+∠D=90°;④ ∠DEB=2∠ABC.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
10.如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若∠AOB=40°,则∠MPN的度数是( )
A.90° B.100° C.120° D.140°
11.如图,,M,N分别是边上的定点,P,Q分别是边上的动点,记,当的值最小时,关于,的数量关系正确的是( )
A. B. C. D.
12.如图,,、、分别平分的外角、内角、外角.以下结论:①:②;③;④平分;⑤.其中错误的结论有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(本大题共6小题,每小题3分,共18分)
13.甲和乙玩一个猜数游戏,规则如下:已知五张纸牌上分别写有1、2、3、4、5五个数字,现甲、乙两人分别从中各自随机抽取一张,然后根据自己手中的数推测谁手上的数更大.甲看了看自己手中的数,想了想说:我不知道谁手中的数更大;乙听了甲的判断后,思索了一下说:我也不知道谁手中的数更大.假设甲、乙所作出的推理都是正确的,那么乙手中的数是____.
14.已知Rt△ABC中,∠C=90°,将∠C沿DE向三角形内折叠,使点C落在△ABC的内部,如图,则∠1+∠2=___度.
15.如图,在中,,与的平分线交于点,得;与的平分线相交于点,得;;与的平分线相交于点,得,则______.
16.如图,将一副三角板按如图所示放置,,,,且,则下列结论中:①;②若平分,则有;③将三角形绕点旋转,使得点落在线段上,则此时;④若,则.其中结论正确的选项有______.(写出所有正确结论的序号)
17.如图,在平面直角坐标系中,为坐标原点,点的坐标为,点的坐标为,点是直线:上的一个动点,若,则点的坐标是__________.
18.如图,在中,和的平分线、相交于点,交于点,交 于点,过点作于点,则下列三个结论:①;②当时,;③若,,则.其中正确的是______.
三、解答题(本大题共8小题,共66分.)
19.(1)学行线以后,香橙同学想出了过一点画一条直线的平行线的新方法,她是通过折纸做的,过程如(图1).
①请你仿照以上过程,在图2中画出一条直线b,使直线b经过点P,且,要求保留折纸痕迹,画出所用到的直线,指明结果.无需写画法:
②在(1)中的步骤(b)中,折纸实际上是在寻找过点P的直线a的 线.
(2)已知,如图3,,BE平分,CF平分.求证:(写出每步的依据).
20.如图所示,点B,E,C,F在同一条直线上,能否由,来证明AC∥DE?如果能,请给出证明;如果不能,请从下列四个条件中再选择一个合适的条件,使AC∥DE成立,并说明理由.供选择的四个条件:①;②;③AB∥DF;④.
21.已知:如图,点E在线段CD上,EA、EB分别平分∠DAB和∠ABC,∠AEB=90°,设AD=x,BC=y,且(x﹣2)2+|y﹣5|=0.
(1)求AD和BC的长.(2)试说线段AD与BC有怎样的位置关系?并证明你的结论.
(3)你能求出AB的长吗?若能,请写出推理过程,若不能,说明理由.
22.如图1,已知线段AB、CD相交于点O,连接AC、BD.(1)求证:∠A+∠C=∠B+∠D;(2)如图2,∠CAB与∠BD的平分线AP、DP相交于点P,求证:∠B+∠C=2∠P.
23.如图,直线AB∥直线CD,线段EF∥CD,连接BF、CF.
(1)求证:∠ABF+∠DCF=∠BFC;(2)连接BE、CE、BC,若BE平分∠ABC,BE⊥CE,求证:CE平分∠BCD;(3)在(2)的条件下,G为EF上一点,连接BG,若∠BFC=∠BCF,∠FBG=2∠ECF,∠CBG=70°,求∠FBE的度数.
24.综合与探究:小新在学习过程中,发现课本有一道习题,他在思考过程中,对习题做了一定变式,让我们来一起看一下吧.在中,与的平分线相交于点.
(1)如图,如果,求的度数.
(2)在()的条件下,如图2,作的外角,的平分线交于点,求的度数.
(3)如图,作的外角,的平分线交于点,延长线段,交于点,在中,是否存在一个内角等于另一个内角的倍,若存在,请直接写出的度数;若不存在,请说明理由.
25.点E在射线DA上,点F、G为射线BC.上两个动点,满足∠DBF=∠DEF,∠BDG=∠BGD,DG平分∠BDE.(1)如图,当点G在F右侧时,求证:;
(2)如图,当点G在BF左侧时,求证:;(3)如图,在(2)的条件下,P为BD延长线上一点,DM平分∠BDG,交BC于点M,DN平分∠PDM,交EF于点N,连接NG,若DG⊥NG,,求∠B的度数.
26.如图,在平面直角坐标系中,A为轴上的一动点,B(0,3),BAC=,AB=AC.
(1)如图1,若,点C在第二象限,求C点坐标;
(2)如图2,当点C在第四象限时,点F与点B关于轴对称,连接CF并延长交轴于点E,求点E坐标;(3)如图3,P为第二象限的点,点H在线段PF上,且,当点E在轴负半轴上,点F在y轴负半轴上运动时,且OE=OF,求m、n之间的数量关系.
答案
一、选择题
A.B.B.B.A.D.A.C.D.B.B.B.
二、填空题
13.3
14.
15.
16.②③④
17.或
18.①②
三、解答题
19.(1)解:①如图2所示:
②在(1)中的步骤(b)中,折纸实际上是在寻找过点的直线的垂线.故答案为垂;
(2)证明:平分,平分(已知),,(角平分线的定义),
(已知),(两直线平行,内错角相等),
(等量代换),(等式性质),(内错角相等,两直线平行).
20.解:由AC=DE,BE=FC无法证明,
选择条件②AB=DF进行证明,
∵BE=FC,∴BE+CE=FC+CE,∴BC=FE,
在△ABC和△DFE中,,
∴△ABC≌△DFE(SSS),∴∠ACB=∠DFE,∴;
选择条件④ ,
∵,∴三角形ABC和三角形DFE都是直角三角形,
在Rt△ABC和Rt△DFE中,∴Rt△ABC≌Rt△DFE(HL),
∴∠ACB=∠DFE,∴.
21.解:(1),,,解得,,即,;
(2).理由如下:、分别平分和,
,,,
,,,;
(3)能.理由如下:延长交直线于,如图,
,,而,,
在△AEB和△FEB中,
∴△AEB≌△FEB(AAS),AE=EF.
在△ADE和△FCE中,
,,.
22.证明:(1)在△AOC中,∠A+∠C=180°﹣∠AOC,
在△BOD中,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,∴∠A+∠C=∠B+∠D;
(2)在AP、CD相交线中,有∠CAP+∠C=∠P+∠CDP,
在AB、DP相交线中,有∠B+∠BDP=∠P+∠BAP,
∴∠B+∠C+∠CAP+∠BDP=2∠P+∠CDP+∠BAP,
∵AP、DP分别平分∠CAB、∠BDC,∴∠CAP=∠BAP,∠BDP=∠CDP,∴∠B+∠C=2∠P.
23.证明:(1)∵AB∥CD,EF∥CD,∴AB∥EF,∴∠ABF=∠BFE,
∵EF∥CD,∴∠DCF=∠EFC,∴∠BFC=∠BFE+∠EFC=∠ABF+∠DCF;
(2)∵BE⊥EC,∴∠BEC=90°,∴∠EBC+∠BCE=90°,
由(1)可得:∠BFC=∠ABE+∠ECD=90°,∴∠ABE+∠ECD=∠EBC+∠BCE,
∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ECD=∠BCE,∴CE平分∠BCD;
(3)设∠BCE=β,∠ECF=γ,
∵CE平分∠BCD,∴∠DCE=∠BCE=β,
∴∠DCF=∠DCE﹣∠ECF=β﹣γ,∴∠EFC=β﹣γ,
∵∠BFC=∠BCF,∴∠BFC=∠BCE+∠ECF=γ+β,∴∠ABF=∠BFE=2γ,
∵∠FBG=2∠ECF,∴∠FBG=2γ,∴∠ABE+∠DCE=∠BEC=90°,
∴∠ABE=90°﹣β,∴∠GBE=∠ABE﹣∠ABF﹣∠FBG=90°﹣β﹣2γ﹣2γ,
∵BE平分∠ABC,∴∠CBE=∠ABE=90°﹣β,∴∠CBG=∠CBE+∠GBE,
∴70°=90°﹣β+90°﹣β﹣2γ﹣2γ,整理得:2γ+β=55°,
∴∠FBE=∠FBG+∠GBE=2γ+90°﹣β﹣2γ﹣2γ=90°﹣(2γ+β)=35°.
24.解:(1),.
点是和的平分线的交点,.
(2)外角,的角平分线交于点,
∴,
.
(3)存在,的度数为或或 如图,延长至,
∵为的外角的角平分线,∴是的外角的平分线,∴
∵平分,∴
∵,∴,即.
又∵,∴,即.
,
如果在中存在一个内角等于另一个内角的倍,那么分四种情况:
①,则;
②,则,,;
③,则,解得
④,则,解得.
综上所述,的度数是或或
25.解:(1)∵DG平分∠BDE,∴∠BDG=∠ADG,
又∵∠BDG=∠BGD,∴∠ADG=∠DGB,∴,∴∠DEF=∠EFG,
∵∠DBF=∠DEF,∴∠DBF=∠EFG,∴;
(2)过点G作交AD于K,同理可证,
∴,∴∠BDG=∠DGK,∠GEF=∠KGE,
∴∠DGE=∠DGK+∠KGE,∴∠DGE=∠BDG+∠FEG;
(3)设,则,,,∵DN平分∠PDM,∴,
∴,,
∵DG⊥NG,∴,∴,
∵,∴,
∵,∴,∴,∴.
26.(1)过点C作交OA于点D,
∵,∴. , . , .
,.
在和中
, , ;
(2)过点C作交AE于点G,
∵,∴,. , .
,.
在和中
, , .
∵点F与点B关于轴对称, .设直线FC的解析式为,
将,代入解析式中得 解得
∴直线FC的解析式为. 令,则,解得, ∴;
(3),理由如下:设直线OH的解析式为,
,, , ∴直线OH的解析式为.
,. 设直线PF的解析式为 ,
将代入解析式中得 ,∴直线PF的解析式为 .
当时,,, .
,, ,, ,
设直线PE的解析式为, 将代入解析式中得,
∴直线PE的解析式为.
解得点P的纵坐标为,, .
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
