北师大版八年级数学上册试题 第四章 一次函数单元检测卷(含答案)
文档属性
| 名称 | 北师大版八年级数学上册试题 第四章 一次函数单元检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 660.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 14:02:07 | ||
图片预览



文档简介
第四章 一次函数单元检测卷
一、选择题(本大题共12小题,每小题3分,共36分)
1.下列函数中,自变量取值范围错误的是( )
A. B.
C.为任意实数) D.
2.下列函数,是正比例函数的是( )
A. B. C. D.
3.一次函数的部分x和y的部分对应值如下表所示,下列结论正确的是( )
x …… 0 1 2 ……
y …… 5 2 ……
A.y随x的增大而增大 B.是方程的解
C.此函数图象不经过第三象限 D.此函数图象与x轴交于点
4.下列不能表示是的函数的是( )
A. B.
C. D.
5.若一次函数(为常数且)的图像经过点(-2,0),则关于的方程的解为( )
A. B. C. D.
6.在平面直角坐标系中,若点(x1,-1),(x2,-2),(x3,1)都在直线y=-2x+b上,则x1,x2,x3的大小关系是( )
A.x1>x2>x3 B.x3>x2>x1 C.x2>x1>x3 D.x2>x3>x1
7.如图,直线与直线都经过点,则关于x,y的方程组的解是( )
A. B. C. D.
8.已知关于x的一次函数y=kx+3k+1,不论k为何值,该函数的图象都经过点P,则点P的坐标为( )
A.(﹣3,1) B.(1,﹣3) C.(3,1) D.(1,3)
9.瓶子或者罐头盒等圆柱形的物体常常如图所示那样堆放着,随着层数的增加,物体总数也会发生变化,数据如表,则下列说法错误的是( )
层数n/层 1 2 3 4 5 ……
物体总数y/个 1 3 6 10 15 ……
A.在这个变化过程中层数是自变量,物体总数是因变量
B.当堆放层数为7层时,物体总数为28个
C.物体的总数随着层数的增加而均匀增加
D.物体的总数y与层数n之间的关系式为
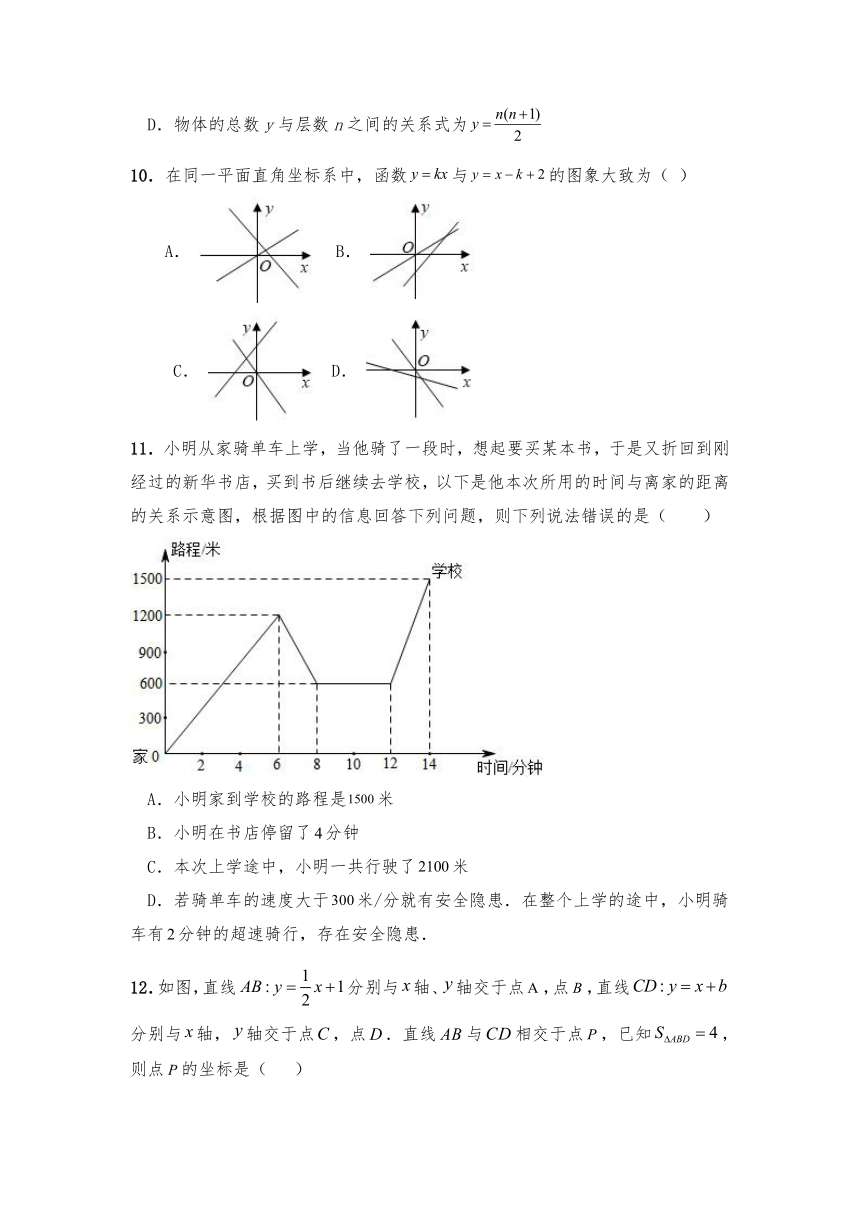
10.在同一平面直角坐标系中,函数与的图象大致为( )
A. B.
C. D.
11.小明从家骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与离家的距离的关系示意图,根据图中的信息回答下列问题,则下列说法错误的是( )
A.小明家到学校的路程是米
B.小明在书店停留了分钟
C.本次上学途中,小明一共行驶了米
D.若骑单车的速度大于米/分就有安全隐患.在整个上学的途中,小明骑车有分钟的超速骑行,存在安全隐患.
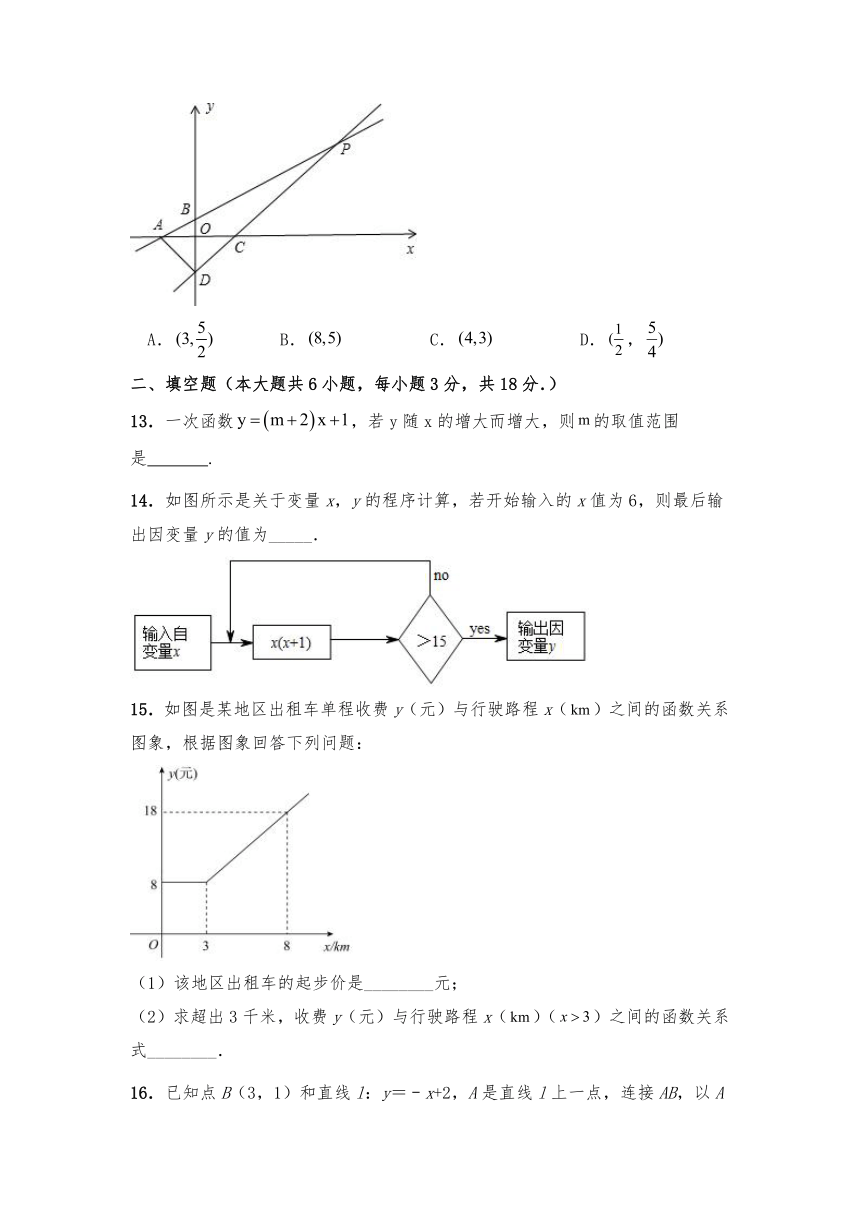
12.如图,直线分别与轴、轴交于点,点,直线分别与轴,轴交于点,点.直线与相交于点,已知,则点的坐标是( )
A. B. C. D.,
二、填空题(本大题共6小题,每小题3分,共18分.)
13.一次函数,若y随x的增大而增大,则的取值范围是 .
14.如图所示是关于变量x,y的程序计算,若开始输入的x值为6,则最后输出因变量y的值为_____.
15.如图是某地区出租车单程收费y(元)与行驶路程x()之间的函数关系图象,根据图象回答下列问题:
(1)该地区出租车的起步价是________元;
(2)求超出3千米,收费y(元)与行驶路程x()()之间的函数关系式________.
16.已知点B(3,1)和直线l:y=﹣x+2,A是直线l上一点,连接AB,以A为直角顶点作等腰直角三角形ABC,使点C落在第一象限,当AC最短时,点C的坐标是 ________.
17.如图,已知直线:,过点作轴的垂线交直线于点,过点作直线的垂线交轴于点;过点作轴的垂线交直线于点,过点作直线的垂线交轴于点;…;按此作法继续下去,则点的坐标为______.
18.如图,直线y=﹣x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则直线AM的解析式是_____.
三、解答题(本大题共8小题,共66分.)
19.定义:对于给定的两个函数,当时,它们对应函数值相等;当时,它们对应的函数值互为相反数.我们称这样的两个函数互为相关函数.
例如:一次函数,它的相关函数为
(1)已知点在一次函数的相关函数的图象上,则的值为______;(2)已知一次函数.①这个函数的相关函数为______;②若点在这个函数的相关函数的图象上,求的值;③当时,这个函数的相关函数的取值范围是,直接写出的取值范围.
20.如图,一次函数y=x+3的图象与x轴交于点B,与过点A(3,0)的一次函数的图象交于点C(1,m).(1)求m的值;(2)求一次函数图象相应的函数表达式;
(3)求的面积.
21.已知A、B两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分别到达目的地后停止.甲、乙两车之间的距离y(千米)与甲车的行驶时间x(时)之间的函数关系如图所示.
(1)乙车的速度为 千米/时;(2)求甲、乙两车相遇后y与x之间的函数关系式;
(3)当甲车到达距B地90千米处时,求甲、乙两车之间的路程.
22.如图,将平行四边形放置在平面直角坐标系中,为坐标原点,若点的坐标是,点的坐标是.
(1)点的坐标为_______;(2)求直线的表达式;(3)若点关于轴的对称点为点,设过点的直线,与四边形有公共点,结合函数图象,求的取值范围.
23.某商店销售5台A型和10台B型电脑的利润为3500元,销售10台A型和10台B型电脑的利润为4500元,(1)求每台A型电脑和B型电脑的销售利润;(2)该商店计划一次购进两种型号的电脑共80台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这80台电脑的销售总利润为y元.①求y关于x的函数关系式;②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?(3)实际进货时,厂家对A型电脑出厂价下调元,且限定商店销售B型电脑的利润不低于10000元,若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这80台电脑销售总利润最大的进货方案.
24.问题:探究函数的图象与性质.
小华根据学习函数的经验,对函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
在函数中,自变量可以是任意实数; (1)下表是与的几组对应值.
… -3 -2 -1 0 1 2 3 …
… 1 0 -1 -2 -1 0 …
①______;②若,为该函数图象上不同的两点,则______;
(2)如图,在平面直角坐标系中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;(3)根据函数图象可得函数的性质:①该函数的最小值为_____;②再写出该函数一条性质_______.
25.直线AB:y=-x+b分别与x,y轴交于A(8,0)、B两点,过点B的直线交x轴轴负半轴于C,且OB:OC=4:3.
(1)求点B的坐标为 __________;(2)求直线BC的解析式;(3)动点M从C出发沿射线CA方向运动,运动的速度为每秒1个单位长度.设M运动t秒时,当t为何值时△BCM为等腰三角形.
26.如图,正方形的边长为4,在x轴上,在y轴上,且,,点D为的中点,点E在x轴上,直线交x轴于点F.(1)如图1,若,①求证:;②点P是直线上的一个动点,求作点P使得的值最小,并直接写出的最小值;(2)如图2,E在x轴上运动,当为等腰三角形时,求点E的坐标.
答案
一、选择题
D.C.C.B.C.C.D.A.C.C.C.B
二、填空题
13..
14.42
15.(1)8元;(2)
16.(1,1)
17.
18.y=﹣+3.
三、解答题
19.由题意知:一次函数,它的相关函数为,
把x=-1代入 y= x+2 的相关函数得:y=-3,故答案为:;
(2)①;②的相关函数是,
当时,,解得;当时,,解得;∴或2;
③当n≥0时,x=n代入函数则:y=2n-1,x=n+1代入函数则:y=2(n+1)-1=2n+1,
∵2n-1<2n+1,∴-2n+1=-1,2n+1=3,∴n=1,则
当n+1<0时,x=n代入函数则:y=-2n+1,x=n+1代入函数则:y=-2(n+1)+1=-2n-1,
∵-2n+1>-2n-1,∴-2n+1=3,则n=-1(舍去);
当n+1≥0,n<0,即-1≤n<0时,x=n代入函数则:y=-2n+1,x=n+1代入函数则:y=2(n+1)-1=2n+1,
∵-2n+1>2n+1,∴-2n+1=3,2n+1=-1,∴n=-1,则 综上所述:.
20.解:(1)∵点C(1,m)在一次函数y=x+3的图象上,∴m=1+3=4;
(2)设一次函数图象相应的函数表达式为y=kx+b,
把点A(3,0),C(1,4)代入得,解得,
∴一次函数图象相应的函数表达式y=﹣2x+6;
(3)∵一次函数y=x+3的图象与x轴交于点B,∴B(﹣3,0),
∵A(3,0),C(1,4),∴AB=6,∴.
21.(1)由图可得,乙车的速度为:270÷2﹣60=75(千米/时),故答案为:75;
(2)a=270÷75=3.6,故当a=3.6时,两车之间的距离为:60×3.6=216(千米),b=270÷60=4.5,
当2<x≤3.6时,设y与x之间的函数关系式为y=kx+b,
,解得,,
即当2<x≤3.6时,y与x之间的函数关系式为y=135x﹣270;
当3.6<x≤4.5时,设y与x之间的函数关系式为y=mx+n,
,解得,,
即当3.6<x≤4.5时,y与x之间的函数关系式为y=60x;
由上可得,甲、乙两车相遇后,y与x之间的函数关系式为y=;
(3)∵甲车到达距B地90千米处时,x==3,
∴将x=3代入y=135x﹣270,得:y=135×3﹣270=135,
即当甲车到达距B地90千米处时,甲、乙两车之间的路程是135千米.
22.解:(1)∵四边形ABCO是平行四边形,O为坐标原点,点A的坐标是(6,0),点C的坐标是(1,4),∴BC=OA=6,6+1=7,∴点B的坐标是(7,4),故答案为:(7,4);
(2)设直线AC的表达式为:y=kx+b,∵点A的坐标是(6,0),点C的坐标是(1,4),
∴,解得:,∴直线AC的表达式为:y=;
(3)∵点C关于x轴的对称点为点E,点C的坐标是(1,4),∴E(1,4),
把O(0,0)和E(1,-4)代入y=kx+b得y=-4x;
把A(6,0)和E(1,-4)代入y=kx+b得y=;
把B(7,4)和E(1,-4)代入y=kx+b得y=;∴k的取值范围为:k≤-4或k≥
23.解:(1)设每台A型电脑销售利润为a元,每台B型电脑的销售利润为b元;根据题意得
,解得,
答:每台A型电脑销售利润为200元,每台B型电脑的销售利润为250元;
(2)①据题意得,y=200x+250(80 x),即y= 50x+20000,
②据题意得,80 x≤2x,解得x≥26,
∵y= 50x+20000, 50<0,∴y随x的增大而减小,
∵x为正整数,∴当x=27时,y取最大值,则80 x=53,
即商店购进27台A型电脑和53台B型电脑的销售利润最大;
(3)据题意得,y=(200+m)x+250(80 x),即y=(m 50)x+20000,
∵250(80 x)≥10000,解得:x≤40, 26≤x≤40,且为正整数,
①0<m<50时,y随x的增大而减小,∴当x=27时,y取最大值,
即商店购进27台A型电脑和53台B型电脑的销售利润最大.
②m=50时,m 50=0,,
即商店购进A型电脑数量满足26≤x≤40的整数时,均获得最大利润;
③当50<m<100时,m 50>0,y随x的增大而增大,∴当x=40时,y取得最大值.
即商店购进40台A型电脑和40台B型电脑的销售利润最大.
24.解:(1)①把x=3代入y=|x|-2,得m=3-2=1.故答案为1;
②把y=8代入y=|x|-2,得8=|x|-2,解得x=-10或10,
∵A(n,8),B(10,8)为该函数图象上不同的两点,∴n=-10.故答案为-10;
(2)该函数的图象如图所示,
(3)①有图像可知,该函数的最小值为-2;故答案为-2;
②当x>0时,y随x的增大而增大,当x<0时,y随x的增大而减小.
故答案为:当x>0时,y随x的增大而增大,当x<0时,y随x的增大而减小.
25.解:(1)y=﹣x+b分别与x轴交于A(8、0),得:﹣8+b=0.解得b=8,即函数解析式为y=﹣x+8,当x=0时,y=8,B点坐标是(0,8);
(2)由OB:OC=4:3,BC=8,得:8:BC=4:3,解得BC=6,即C(﹣6,0),设直线BC的解析式为y=kx+b,图象经过点B,C,得:,解得: ,∴直线BC的解析式为y=x+8;
(3)设M点坐标(a,0),由勾股定理得:BC==10,分三种情况讨论:
①当MC=BC=10时,由路程处以速度等于时间,得10÷1=10(秒),即M运动10秒,△BCM为等腰三角形;
②当MC=MB时,MC2=MB2,即(a+6)2=a2+82,化简,得12a=28,解得a=即M(,0).MC=﹣(﹣6)=+6=,由路程除以速度等于时间,得÷1=(秒),即M运动秒时,△BCM为等腰三角形;
③当BC=BM时,得OC=OM=6,即MC=6﹣(﹣6)=6+6=12,由路程除以速度等于时间,得12÷1=12(秒),即M运动12秒时,△BCM为等腰三角形.
综上所述:t=10(秒),t=(秒),t=12(秒)时,△BCM为等腰三角形.
26.(1)①∵正方形ABCO的边长为4,∴OC=OA=AB=BC=4,∠B=∠DAE=∠COE=90,
∵点D为AB的中点,∴BD=AD=2,
在Rt△BCD中,,
在Rt△ADE中,,
在Rt△OCE中,,∴,
勾股定理的逆定理可知,△EDC为直角三角形,且∠CDE=90,故∠CDE=90;
②如图,作点A关于DE的对称点为,连接交DE于点H,连接交DE于P,点P为所求作,
由对称性可知,,,
∴PA+PF=+PF,PA+PF取得最小值,最小值,
由题意知A(4,0),D(4,2),C(0,4),B(4,4),E(3,0),
设直线CD的解析式为,
∴,解得:,∴直线CD的解析式为,
当时,,∴点的坐标为(8,0),同理求得直线DE的解析式为,
∵,∴∥CF,∴设直线的解析式为,
把A(4,0)代入得,,∴,∴直线的解析式为,
联立,解得:,∴点的坐标为(,),
又,∴,,
∴,,∴点的坐标为(,),∴,
∴,∴PA+PF的最小值为;
(2)∵E在x轴上运动,∴设点的坐标为(,),
∵△ECD为等腰三角形,∴CD=CE或EC=ED或CD=DE,
∵C(0,4),D(4,2),E(,),∴,
,,
①当CD=CE时,则,∴,解得,∴(,),(,);
②当EC=ED时,则,∴,解得,∴(,);
③当CD=DE时,则,∴,解得,,
时,E与F重合,C、D、E共线,无法构成三角形;∴(,);
综上所述,当△ECD为等腰三角形时,点的坐标为(,)或(,)或(,)或(,).
一、选择题(本大题共12小题,每小题3分,共36分)
1.下列函数中,自变量取值范围错误的是( )
A. B.
C.为任意实数) D.
2.下列函数,是正比例函数的是( )
A. B. C. D.
3.一次函数的部分x和y的部分对应值如下表所示,下列结论正确的是( )
x …… 0 1 2 ……
y …… 5 2 ……
A.y随x的增大而增大 B.是方程的解
C.此函数图象不经过第三象限 D.此函数图象与x轴交于点
4.下列不能表示是的函数的是( )
A. B.
C. D.
5.若一次函数(为常数且)的图像经过点(-2,0),则关于的方程的解为( )
A. B. C. D.
6.在平面直角坐标系中,若点(x1,-1),(x2,-2),(x3,1)都在直线y=-2x+b上,则x1,x2,x3的大小关系是( )
A.x1>x2>x3 B.x3>x2>x1 C.x2>x1>x3 D.x2>x3>x1
7.如图,直线与直线都经过点,则关于x,y的方程组的解是( )
A. B. C. D.
8.已知关于x的一次函数y=kx+3k+1,不论k为何值,该函数的图象都经过点P,则点P的坐标为( )
A.(﹣3,1) B.(1,﹣3) C.(3,1) D.(1,3)
9.瓶子或者罐头盒等圆柱形的物体常常如图所示那样堆放着,随着层数的增加,物体总数也会发生变化,数据如表,则下列说法错误的是( )
层数n/层 1 2 3 4 5 ……
物体总数y/个 1 3 6 10 15 ……
A.在这个变化过程中层数是自变量,物体总数是因变量
B.当堆放层数为7层时,物体总数为28个
C.物体的总数随着层数的增加而均匀增加
D.物体的总数y与层数n之间的关系式为
10.在同一平面直角坐标系中,函数与的图象大致为( )
A. B.
C. D.
11.小明从家骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与离家的距离的关系示意图,根据图中的信息回答下列问题,则下列说法错误的是( )
A.小明家到学校的路程是米
B.小明在书店停留了分钟
C.本次上学途中,小明一共行驶了米
D.若骑单车的速度大于米/分就有安全隐患.在整个上学的途中,小明骑车有分钟的超速骑行,存在安全隐患.
12.如图,直线分别与轴、轴交于点,点,直线分别与轴,轴交于点,点.直线与相交于点,已知,则点的坐标是( )
A. B. C. D.,
二、填空题(本大题共6小题,每小题3分,共18分.)
13.一次函数,若y随x的增大而增大,则的取值范围是 .
14.如图所示是关于变量x,y的程序计算,若开始输入的x值为6,则最后输出因变量y的值为_____.
15.如图是某地区出租车单程收费y(元)与行驶路程x()之间的函数关系图象,根据图象回答下列问题:
(1)该地区出租车的起步价是________元;
(2)求超出3千米,收费y(元)与行驶路程x()()之间的函数关系式________.
16.已知点B(3,1)和直线l:y=﹣x+2,A是直线l上一点,连接AB,以A为直角顶点作等腰直角三角形ABC,使点C落在第一象限,当AC最短时,点C的坐标是 ________.
17.如图,已知直线:,过点作轴的垂线交直线于点,过点作直线的垂线交轴于点;过点作轴的垂线交直线于点,过点作直线的垂线交轴于点;…;按此作法继续下去,则点的坐标为______.
18.如图,直线y=﹣x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则直线AM的解析式是_____.
三、解答题(本大题共8小题,共66分.)
19.定义:对于给定的两个函数,当时,它们对应函数值相等;当时,它们对应的函数值互为相反数.我们称这样的两个函数互为相关函数.
例如:一次函数,它的相关函数为
(1)已知点在一次函数的相关函数的图象上,则的值为______;(2)已知一次函数.①这个函数的相关函数为______;②若点在这个函数的相关函数的图象上,求的值;③当时,这个函数的相关函数的取值范围是,直接写出的取值范围.
20.如图,一次函数y=x+3的图象与x轴交于点B,与过点A(3,0)的一次函数的图象交于点C(1,m).(1)求m的值;(2)求一次函数图象相应的函数表达式;
(3)求的面积.
21.已知A、B两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分别到达目的地后停止.甲、乙两车之间的距离y(千米)与甲车的行驶时间x(时)之间的函数关系如图所示.
(1)乙车的速度为 千米/时;(2)求甲、乙两车相遇后y与x之间的函数关系式;
(3)当甲车到达距B地90千米处时,求甲、乙两车之间的路程.
22.如图,将平行四边形放置在平面直角坐标系中,为坐标原点,若点的坐标是,点的坐标是.
(1)点的坐标为_______;(2)求直线的表达式;(3)若点关于轴的对称点为点,设过点的直线,与四边形有公共点,结合函数图象,求的取值范围.
23.某商店销售5台A型和10台B型电脑的利润为3500元,销售10台A型和10台B型电脑的利润为4500元,(1)求每台A型电脑和B型电脑的销售利润;(2)该商店计划一次购进两种型号的电脑共80台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这80台电脑的销售总利润为y元.①求y关于x的函数关系式;②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?(3)实际进货时,厂家对A型电脑出厂价下调元,且限定商店销售B型电脑的利润不低于10000元,若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这80台电脑销售总利润最大的进货方案.
24.问题:探究函数的图象与性质.
小华根据学习函数的经验,对函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
在函数中,自变量可以是任意实数; (1)下表是与的几组对应值.
… -3 -2 -1 0 1 2 3 …
… 1 0 -1 -2 -1 0 …
①______;②若,为该函数图象上不同的两点,则______;
(2)如图,在平面直角坐标系中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;(3)根据函数图象可得函数的性质:①该函数的最小值为_____;②再写出该函数一条性质_______.
25.直线AB:y=-x+b分别与x,y轴交于A(8,0)、B两点,过点B的直线交x轴轴负半轴于C,且OB:OC=4:3.
(1)求点B的坐标为 __________;(2)求直线BC的解析式;(3)动点M从C出发沿射线CA方向运动,运动的速度为每秒1个单位长度.设M运动t秒时,当t为何值时△BCM为等腰三角形.
26.如图,正方形的边长为4,在x轴上,在y轴上,且,,点D为的中点,点E在x轴上,直线交x轴于点F.(1)如图1,若,①求证:;②点P是直线上的一个动点,求作点P使得的值最小,并直接写出的最小值;(2)如图2,E在x轴上运动,当为等腰三角形时,求点E的坐标.
答案
一、选择题
D.C.C.B.C.C.D.A.C.C.C.B
二、填空题
13..
14.42
15.(1)8元;(2)
16.(1,1)
17.
18.y=﹣+3.
三、解答题
19.由题意知:一次函数,它的相关函数为,
把x=-1代入 y= x+2 的相关函数得:y=-3,故答案为:;
(2)①;②的相关函数是,
当时,,解得;当时,,解得;∴或2;
③当n≥0时,x=n代入函数则:y=2n-1,x=n+1代入函数则:y=2(n+1)-1=2n+1,
∵2n-1<2n+1,∴-2n+1=-1,2n+1=3,∴n=1,则
当n+1<0时,x=n代入函数则:y=-2n+1,x=n+1代入函数则:y=-2(n+1)+1=-2n-1,
∵-2n+1>-2n-1,∴-2n+1=3,则n=-1(舍去);
当n+1≥0,n<0,即-1≤n<0时,x=n代入函数则:y=-2n+1,x=n+1代入函数则:y=2(n+1)-1=2n+1,
∵-2n+1>2n+1,∴-2n+1=3,2n+1=-1,∴n=-1,则 综上所述:.
20.解:(1)∵点C(1,m)在一次函数y=x+3的图象上,∴m=1+3=4;
(2)设一次函数图象相应的函数表达式为y=kx+b,
把点A(3,0),C(1,4)代入得,解得,
∴一次函数图象相应的函数表达式y=﹣2x+6;
(3)∵一次函数y=x+3的图象与x轴交于点B,∴B(﹣3,0),
∵A(3,0),C(1,4),∴AB=6,∴.
21.(1)由图可得,乙车的速度为:270÷2﹣60=75(千米/时),故答案为:75;
(2)a=270÷75=3.6,故当a=3.6时,两车之间的距离为:60×3.6=216(千米),b=270÷60=4.5,
当2<x≤3.6时,设y与x之间的函数关系式为y=kx+b,
,解得,,
即当2<x≤3.6时,y与x之间的函数关系式为y=135x﹣270;
当3.6<x≤4.5时,设y与x之间的函数关系式为y=mx+n,
,解得,,
即当3.6<x≤4.5时,y与x之间的函数关系式为y=60x;
由上可得,甲、乙两车相遇后,y与x之间的函数关系式为y=;
(3)∵甲车到达距B地90千米处时,x==3,
∴将x=3代入y=135x﹣270,得:y=135×3﹣270=135,
即当甲车到达距B地90千米处时,甲、乙两车之间的路程是135千米.
22.解:(1)∵四边形ABCO是平行四边形,O为坐标原点,点A的坐标是(6,0),点C的坐标是(1,4),∴BC=OA=6,6+1=7,∴点B的坐标是(7,4),故答案为:(7,4);
(2)设直线AC的表达式为:y=kx+b,∵点A的坐标是(6,0),点C的坐标是(1,4),
∴,解得:,∴直线AC的表达式为:y=;
(3)∵点C关于x轴的对称点为点E,点C的坐标是(1,4),∴E(1,4),
把O(0,0)和E(1,-4)代入y=kx+b得y=-4x;
把A(6,0)和E(1,-4)代入y=kx+b得y=;
把B(7,4)和E(1,-4)代入y=kx+b得y=;∴k的取值范围为:k≤-4或k≥
23.解:(1)设每台A型电脑销售利润为a元,每台B型电脑的销售利润为b元;根据题意得
,解得,
答:每台A型电脑销售利润为200元,每台B型电脑的销售利润为250元;
(2)①据题意得,y=200x+250(80 x),即y= 50x+20000,
②据题意得,80 x≤2x,解得x≥26,
∵y= 50x+20000, 50<0,∴y随x的增大而减小,
∵x为正整数,∴当x=27时,y取最大值,则80 x=53,
即商店购进27台A型电脑和53台B型电脑的销售利润最大;
(3)据题意得,y=(200+m)x+250(80 x),即y=(m 50)x+20000,
∵250(80 x)≥10000,解得:x≤40, 26≤x≤40,且为正整数,
①0<m<50时,y随x的增大而减小,∴当x=27时,y取最大值,
即商店购进27台A型电脑和53台B型电脑的销售利润最大.
②m=50时,m 50=0,,
即商店购进A型电脑数量满足26≤x≤40的整数时,均获得最大利润;
③当50<m<100时,m 50>0,y随x的增大而增大,∴当x=40时,y取得最大值.
即商店购进40台A型电脑和40台B型电脑的销售利润最大.
24.解:(1)①把x=3代入y=|x|-2,得m=3-2=1.故答案为1;
②把y=8代入y=|x|-2,得8=|x|-2,解得x=-10或10,
∵A(n,8),B(10,8)为该函数图象上不同的两点,∴n=-10.故答案为-10;
(2)该函数的图象如图所示,
(3)①有图像可知,该函数的最小值为-2;故答案为-2;
②当x>0时,y随x的增大而增大,当x<0时,y随x的增大而减小.
故答案为:当x>0时,y随x的增大而增大,当x<0时,y随x的增大而减小.
25.解:(1)y=﹣x+b分别与x轴交于A(8、0),得:﹣8+b=0.解得b=8,即函数解析式为y=﹣x+8,当x=0时,y=8,B点坐标是(0,8);
(2)由OB:OC=4:3,BC=8,得:8:BC=4:3,解得BC=6,即C(﹣6,0),设直线BC的解析式为y=kx+b,图象经过点B,C,得:,解得: ,∴直线BC的解析式为y=x+8;
(3)设M点坐标(a,0),由勾股定理得:BC==10,分三种情况讨论:
①当MC=BC=10时,由路程处以速度等于时间,得10÷1=10(秒),即M运动10秒,△BCM为等腰三角形;
②当MC=MB时,MC2=MB2,即(a+6)2=a2+82,化简,得12a=28,解得a=即M(,0).MC=﹣(﹣6)=+6=,由路程除以速度等于时间,得÷1=(秒),即M运动秒时,△BCM为等腰三角形;
③当BC=BM时,得OC=OM=6,即MC=6﹣(﹣6)=6+6=12,由路程除以速度等于时间,得12÷1=12(秒),即M运动12秒时,△BCM为等腰三角形.
综上所述:t=10(秒),t=(秒),t=12(秒)时,△BCM为等腰三角形.
26.(1)①∵正方形ABCO的边长为4,∴OC=OA=AB=BC=4,∠B=∠DAE=∠COE=90,
∵点D为AB的中点,∴BD=AD=2,
在Rt△BCD中,,
在Rt△ADE中,,
在Rt△OCE中,,∴,
勾股定理的逆定理可知,△EDC为直角三角形,且∠CDE=90,故∠CDE=90;
②如图,作点A关于DE的对称点为,连接交DE于点H,连接交DE于P,点P为所求作,
由对称性可知,,,
∴PA+PF=+PF,PA+PF取得最小值,最小值,
由题意知A(4,0),D(4,2),C(0,4),B(4,4),E(3,0),
设直线CD的解析式为,
∴,解得:,∴直线CD的解析式为,
当时,,∴点的坐标为(8,0),同理求得直线DE的解析式为,
∵,∴∥CF,∴设直线的解析式为,
把A(4,0)代入得,,∴,∴直线的解析式为,
联立,解得:,∴点的坐标为(,),
又,∴,,
∴,,∴点的坐标为(,),∴,
∴,∴PA+PF的最小值为;
(2)∵E在x轴上运动,∴设点的坐标为(,),
∵△ECD为等腰三角形,∴CD=CE或EC=ED或CD=DE,
∵C(0,4),D(4,2),E(,),∴,
,,
①当CD=CE时,则,∴,解得,∴(,),(,);
②当EC=ED时,则,∴,解得,∴(,);
③当CD=DE时,则,∴,解得,,
时,E与F重合,C、D、E共线,无法构成三角形;∴(,);
综上所述,当△ECD为等腰三角形时,点的坐标为(,)或(,)或(,)或(,).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
