三角形的基本概念[下学期]
文档属性
| 名称 | 三角形的基本概念[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 114.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-03 00:00:00 | ||
图片预览



文档简介
课件15张PPT。三角形的基本概念孝南区书院中学 邓志军(一)速度测试: 1、一个三角形的两边的长分别为2cm和9cm,第三边的长是一个奇数,则第三边的长为 ; 2、已知△ABC的三边分别是a、b、c,且满足 ,则△ABC是 三角形;若三边满足 , 则△ABC是 三角形;若关于x的方程
有两个相等的实数根,则△ABC是 三角形。 3、等腰三角形的底边与腰长好是一元二次方程 的两根,当b=7时,该三角形的周长为 ;当b=8时,该三角形的周长为 。 4、三条线段a、b、c满足a<b<c,且a+b>c,则以a、b、c为边 构成三角形;
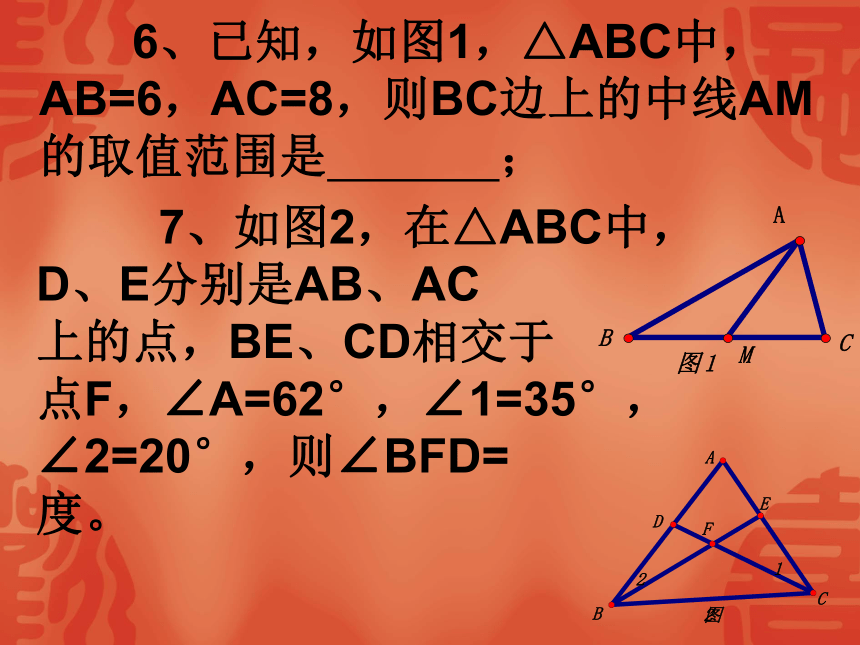
5、已知线段AB=4,BC=3,那么线段AC的长度的取值范围是: 6、已知,如图1,△ABC中,AB=6,AC=8,则BC边上的中线AM的取值范围是 ; 7、如图2,在△ABC中,D、E分别是AB、AC
上的点,BE、CD相交于
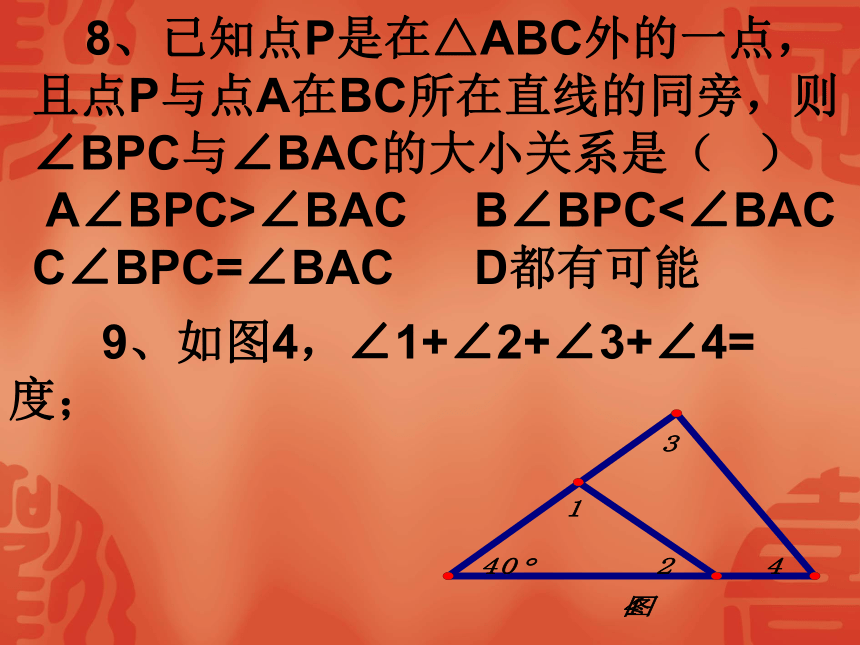
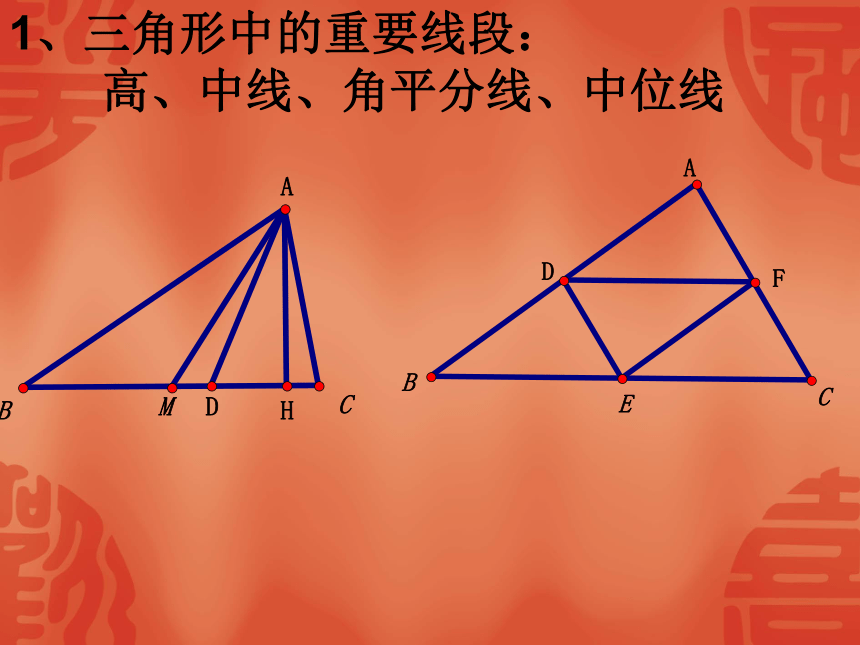
点F,∠A=62°,∠1=35°,∠2=20°,则∠BFD= 度。 8、已知点P是在△ABC外的一点,且点P与点A在BC所在直线的同旁,则∠BPC与∠BAC的大小关系是( ) A∠BPC>∠BAC B∠BPC<∠BAC C∠BPC=∠BAC D都有可能 9、如图4,∠1+∠2+∠3+∠4= 度;1、三角形中的重要线段:
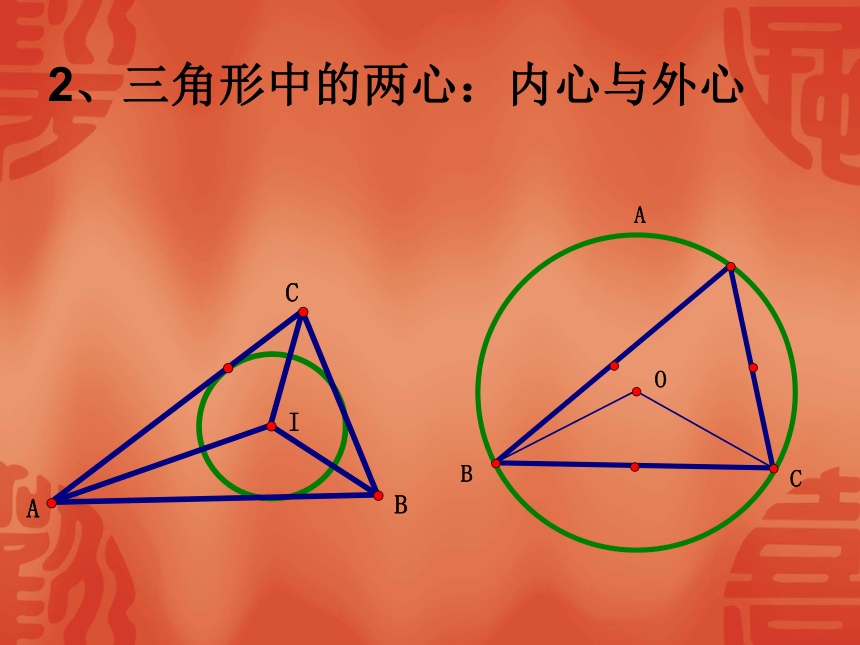
高、中线、角平分线、中位线2、三角形中的两心:内心与外心 3、三角形的分类:4、三角形三边之间的关系:定理:三角形任意两边之和大于第三边;
三角形任意两边之和小于第三边;5、三角形内角和定理及其推论: 定理:三角形的内角和为180° 推论1:三角形的外角和为360°; 推论2:三角形的一个外角等于不相邻
两内角之和; 推论3:三角形的一个外角大于任何一个和它不相邻的内角; (三)例题分析: 例1 如图,D是△ABC的∠C的外角平分线与BA的延长线的交点,求证:∠BAC>∠B
例2 如图,已知在△ABC中,AB>AC,AD是∠A的平分线,点P为AD上任意一点, 求证:AB-AC>PB-PC 例3已知等腰三角形的周长为20,腰长为x,底边长为y,试写出y与x间的函数关系式,并求自变量x的取值范围;例4已知:方程组有两组
不同的实数解;
。且等腰△ABC的三边长是a、b、c,求△ABC的周长。(四)课堂小结: 1、几何中证明线段或角的大小关系问题,通常考虑用三角形的边角关系定理来证明;若遇到线段和差间的大小关系,通常将线段的和差转化为一条线段,再用三角形的三边之间的关系来证明; 2、在解决涉及到三角形的边长的综合题时,一定要注意边长的非负性和三边应满足的关系; 3、若遇到等腰三角形的边长问题时,一定要注意讨论;(五)作业: 《能力检测》P139——P140所有题目;
有两个相等的实数根,则△ABC是 三角形。 3、等腰三角形的底边与腰长好是一元二次方程 的两根,当b=7时,该三角形的周长为 ;当b=8时,该三角形的周长为 。 4、三条线段a、b、c满足a<b<c,且a+b>c,则以a、b、c为边 构成三角形;
5、已知线段AB=4,BC=3,那么线段AC的长度的取值范围是: 6、已知,如图1,△ABC中,AB=6,AC=8,则BC边上的中线AM的取值范围是 ; 7、如图2,在△ABC中,D、E分别是AB、AC
上的点,BE、CD相交于
点F,∠A=62°,∠1=35°,∠2=20°,则∠BFD= 度。 8、已知点P是在△ABC外的一点,且点P与点A在BC所在直线的同旁,则∠BPC与∠BAC的大小关系是( ) A∠BPC>∠BAC B∠BPC<∠BAC C∠BPC=∠BAC D都有可能 9、如图4,∠1+∠2+∠3+∠4= 度;1、三角形中的重要线段:
高、中线、角平分线、中位线2、三角形中的两心:内心与外心 3、三角形的分类:4、三角形三边之间的关系:定理:三角形任意两边之和大于第三边;
三角形任意两边之和小于第三边;5、三角形内角和定理及其推论: 定理:三角形的内角和为180° 推论1:三角形的外角和为360°; 推论2:三角形的一个外角等于不相邻
两内角之和; 推论3:三角形的一个外角大于任何一个和它不相邻的内角; (三)例题分析: 例1 如图,D是△ABC的∠C的外角平分线与BA的延长线的交点,求证:∠BAC>∠B
例2 如图,已知在△ABC中,AB>AC,AD是∠A的平分线,点P为AD上任意一点, 求证:AB-AC>PB-PC 例3已知等腰三角形的周长为20,腰长为x,底边长为y,试写出y与x间的函数关系式,并求自变量x的取值范围;例4已知:方程组有两组
不同的实数解;
。且等腰△ABC的三边长是a、b、c,求△ABC的周长。(四)课堂小结: 1、几何中证明线段或角的大小关系问题,通常考虑用三角形的边角关系定理来证明;若遇到线段和差间的大小关系,通常将线段的和差转化为一条线段,再用三角形的三边之间的关系来证明; 2、在解决涉及到三角形的边长的综合题时,一定要注意边长的非负性和三边应满足的关系; 3、若遇到等腰三角形的边长问题时,一定要注意讨论;(五)作业: 《能力检测》P139——P140所有题目;
