2023秋西师大版五年级数学上册 第五单元 规律堆放的原木问题 课件(共10张PPT)
文档属性
| 名称 | 2023秋西师大版五年级数学上册 第五单元 规律堆放的原木问题 课件(共10张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-28 00:00:00 | ||
图片预览



文档简介
(共10张PPT)
数形结合
规律堆放的原木问题
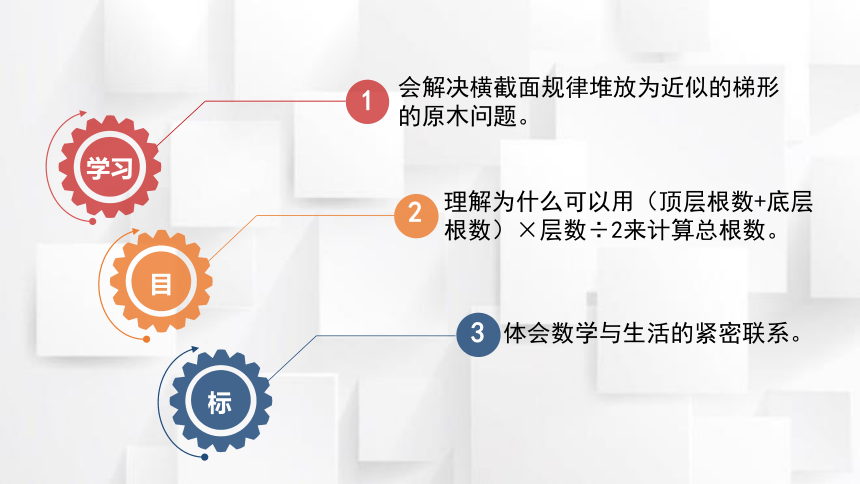
1
2
3
会解决横截面规律堆放为近似的梯形的原木问题。
理解为什么可以用(顶层根数+底层根数)×层数÷2来计算总根数。
体会数学与生活的紧密联系。
学习
目
标
情境导入
院子的一个角落里,堆着像这样摆放的一些原木。
算算院子里的这堆原木—共有多少根
问题探索
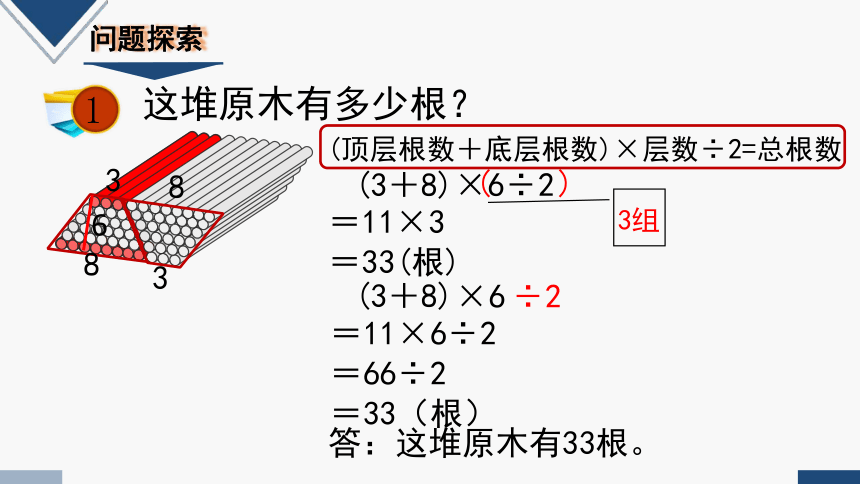
这堆原木有多少根?
1
每相邻两层相差的根数一样多
横截面堆放得像一个梯形
3+4+5+6+7+8=33(根)
=33(根)
(3+8)
+(4+7)
+(5+6)
=11×3
问题探索
这堆原木有多少根?
1
(3+8)×6÷2
(顶层根数+底层根数)×层数÷2=总根数
3
8
3
8
( )
(3+8)
=11×3
=33(根)
×6
÷2
=11×6÷2
=66÷2
=33(根)
答:这堆原木有33根。
3组
6
生活中有一堆原木,它的最下面一层堆了18根,以后每往上堆一层依次少1根,最顶层堆放了1根,请问这堆原木共有多少根?
去伪存真
18×18÷2
=324÷2
=162(根)
(1+18)×18÷2
=19×18÷2
=171(根)
(1+18)×18÷2
=19×18÷2
=171(根)
答:这堆原木一共有171根。
(顶层根数+底层根数)×层数÷2=总根数
课堂测评
(顶层支数+底层支数)×层数÷2=总支数
(4+20)×17÷2
=24×17÷2
=408÷2
=204(支)
答:一共有204支铅笔。
(第一排人数+最后一排人数)×排数÷2=总人数
最后一排人数:(4-1)×4+4=16(人)
或者4×4=16(人)
总人数:(4+16)×4÷2=40(人)
答:这个合唱队一共有40人。
总结回顾
生活中规律堆放的原木和站队列等问题,只要是每相邻两层相差的数量一样多,求总数,都可以用:
(顶层数+底层数)×层数÷2=总数
结
语
谢谢观看
数形结合
规律堆放的原木问题
1
2
3
会解决横截面规律堆放为近似的梯形的原木问题。
理解为什么可以用(顶层根数+底层根数)×层数÷2来计算总根数。
体会数学与生活的紧密联系。
学习
目
标
情境导入
院子的一个角落里,堆着像这样摆放的一些原木。
算算院子里的这堆原木—共有多少根
问题探索
这堆原木有多少根?
1
每相邻两层相差的根数一样多
横截面堆放得像一个梯形
3+4+5+6+7+8=33(根)
=33(根)
(3+8)
+(4+7)
+(5+6)
=11×3
问题探索
这堆原木有多少根?
1
(3+8)×6÷2
(顶层根数+底层根数)×层数÷2=总根数
3
8
3
8
( )
(3+8)
=11×3
=33(根)
×6
÷2
=11×6÷2
=66÷2
=33(根)
答:这堆原木有33根。
3组
6
生活中有一堆原木,它的最下面一层堆了18根,以后每往上堆一层依次少1根,最顶层堆放了1根,请问这堆原木共有多少根?
去伪存真
18×18÷2
=324÷2
=162(根)
(1+18)×18÷2
=19×18÷2
=171(根)
(1+18)×18÷2
=19×18÷2
=171(根)
答:这堆原木一共有171根。
(顶层根数+底层根数)×层数÷2=总根数
课堂测评
(顶层支数+底层支数)×层数÷2=总支数
(4+20)×17÷2
=24×17÷2
=408÷2
=204(支)
答:一共有204支铅笔。
(第一排人数+最后一排人数)×排数÷2=总人数
最后一排人数:(4-1)×4+4=16(人)
或者4×4=16(人)
总人数:(4+16)×4÷2=40(人)
答:这个合唱队一共有40人。
总结回顾
生活中规律堆放的原木和站队列等问题,只要是每相邻两层相差的数量一样多,求总数,都可以用:
(顶层数+底层数)×层数÷2=总数
结
语
谢谢观看
