多边形内角和[下学期]

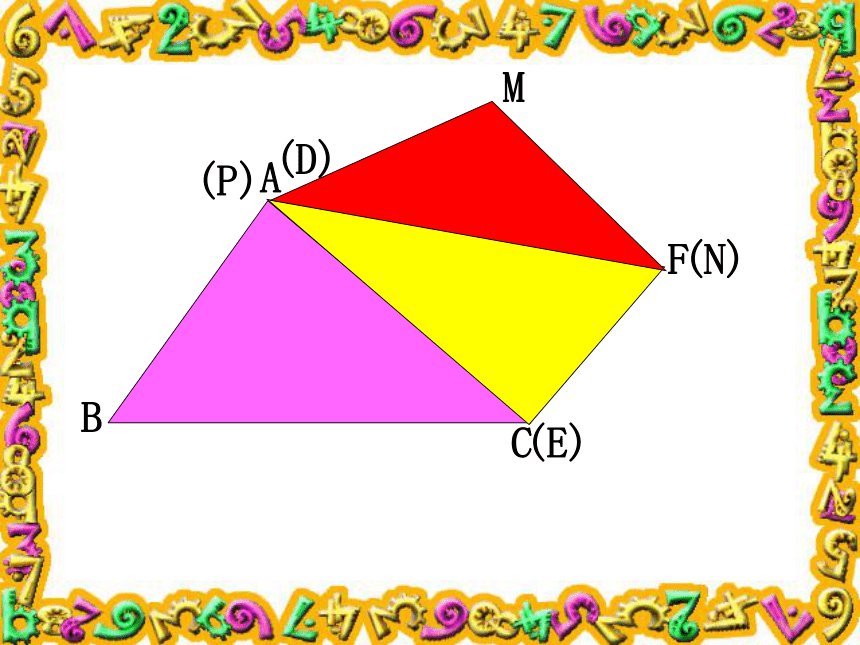
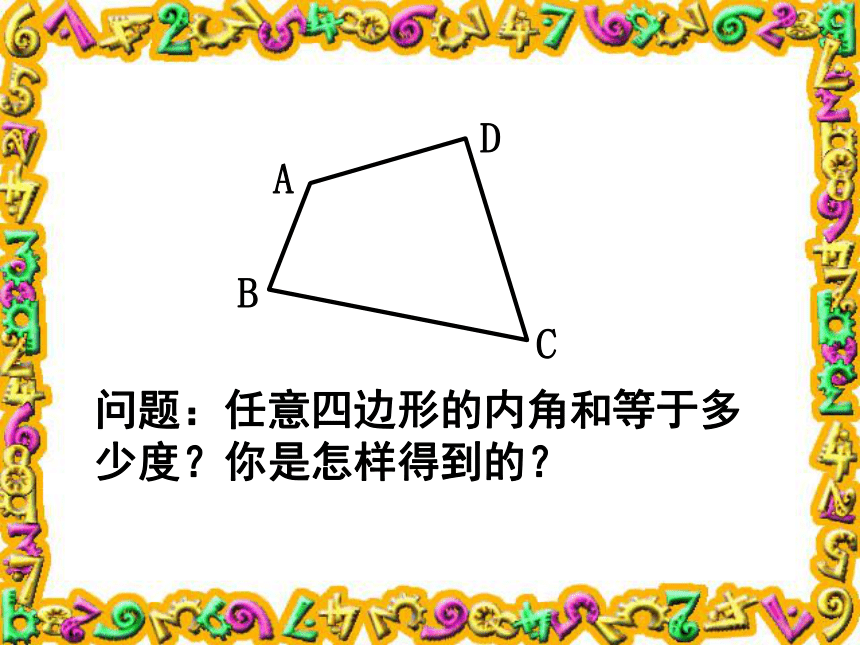
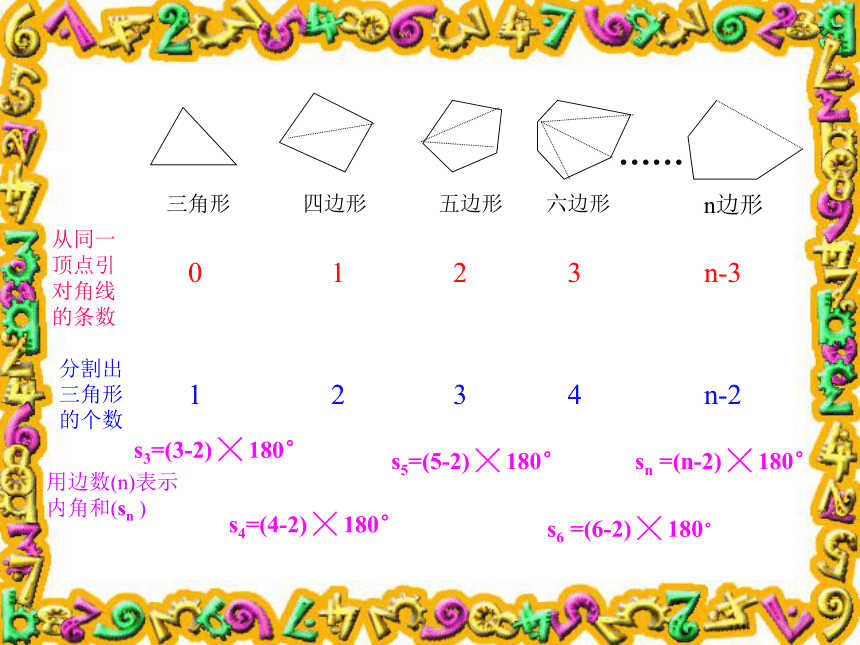
课件19张PPT。探索多边形的内角和∠A+∠B+∠C=? 问题：任意四边形的内角和等于多少度？你是怎样得到的？ 从同一顶点引对角线的条数分割出三角形的个数用边数(n)表示内角和(sn )0123n-31234n-2sn =(n-2) ╳ 180° s6 =(6-2) ╳ 180° s5=(5-2) ╳ 180° s4=(4-2) ╳ 180° s3=(3-2) ╳ 180° 多边形的内角和等于(n-2)╳180°例1.填空题：
（1）在四边形中，它有 条对角线，内角和为 。
（2）八边形的内角和为 ，十边形的内角和为 。
（3）过一多边形的一个顶点可以画10条对角线，那么这个多边形是 边形，内角和为 。
（4）一个多边形的内角和为1260°，那么它的边数为 。 2360°1080°1440°十三1980°9练习1求下列图形中x的值：思考题1.如果一个四边形的一组对角互补，那么另一组对角有什么关系？2.如图，OB⊥AB于B，OC⊥AC于C．问: ∠A与∠1有什么关系？
∠A与∠2有什么关系？ 多边形的外角和解：如图，六边形ABCDEF中，
∠1+∠7=180 °，∠2+∠8=180 °，
∠3+∠9=180 °，∠4+∠10=180 °，
∠5+∠11=180 °，∠6+∠12=180 °.∵ ∠7+∠ 8+∠9+ ∠10 +∠11+ ∠12 =（6－2）×180 °= 720°, 结论：多边形的外角和等于360°.∴ ∠1+∠ 2+∠3+ ∠4 +∠5+ ∠6 = 6×180 °－720 ° = 360°.对于 n 边形，结论仍然成立！小练习：1. 判断题：（1）当多边形的边数增加时，它的外角和也随着增加 .（2）正六边形的每个外角都等于60度 .2. 填空题：（1）正九边形的每一个外角都等于 度. 40 （2）一个多边形的每一个外角都等于30°，
这个多边形是 边形. 正十二7.3.2 多边形的内角和（4）如果多边形的内角和等于外角和，
那么这个多边形是 边形。（1）八边形的内角和等于 度.（2）一个多边形的内角和等于1260° ，
这个多边形是 边形.1080九（3）一个多边形的每一个内角都等于135°，
则这个多边形是 边形.正八2.填空题：四1、如图，五边形ABCDE的内角都相等，且∠1=∠2，∠3=∠4，求x的值。
例2. 已知一个多边形，它的内角和 等于五边形的内角和的2倍，求这个多边形的 边数。



解： 设多边形的边数为n，因为它的内角和等于 (n-2)?180°，
五边形内角和等于540o，所以，
(n-2)?180°=2×540o。
解得: n=8
?这个多边形的边数为8。
（1）已知一个多边形的边数为12，那么它的内角和为 。
（2）已知一个多边形的内角和为1080°，那么它的边数为 。
（3）已知一个正多边形，边数为9，那么它的每一个内角的度数为 。
（4）已知一个正多边形的一个内角为150°，那么它是一个 边形。.填空题1800°8140°正十二
例3. 一个多边形当边数增加1时，它的内角和增加 多少度？




当边数增加1时，

解： 设多边形的边数为n，
因为它的内角和等于 (n-2)?180°，? (n+1-2)?180°- (n-2)?180°
=n?180°-180°-n?180°+360°
= 180°
?内角和增加180°
内角和为(n+1-2)?180°，通过今天的学习你有哪些收获？