12.1 全等三角形(公开课课件)
文档属性
| 名称 | 12.1 全等三角形(公开课课件) |  | |
| 格式 | zip | ||
| 文件大小 | 570.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-11 20:42:55 | ||
图片预览



文档简介
课件23张PPT。 全等三角形12.1同一张底片洗出的照片是
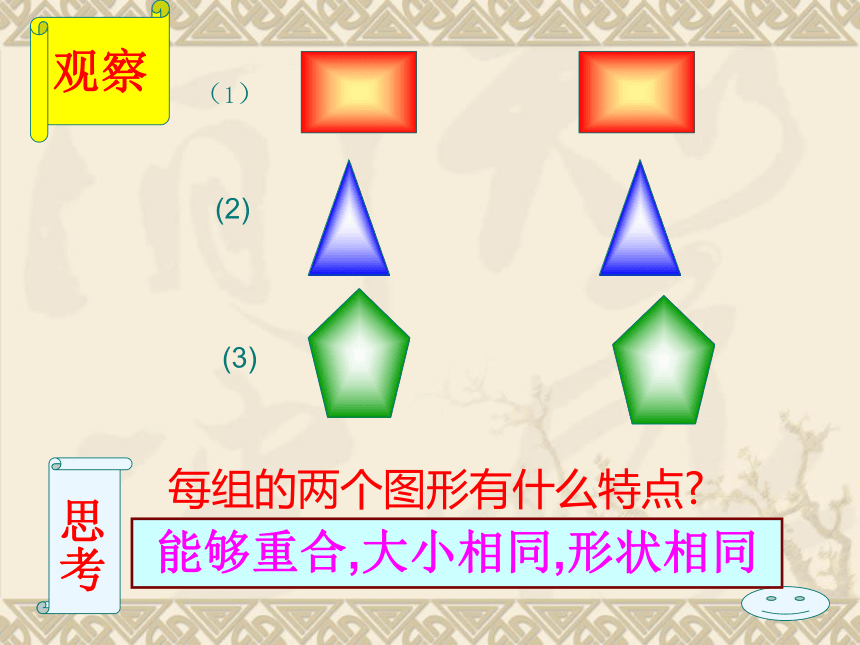
能够完全重合的(1)(2)(3) 思考每组的两个图形有什么特点?观察能够重合,大小相同,形状相同能够完全重合的两个图形叫做全等形:全等图形的特征(1) 你还能说出生活中全等图形的例子吗? (2) 如果两个图形全等,它们的形状大小一定都相同吗?全等图形的形状和大小都相同形状
相同大小
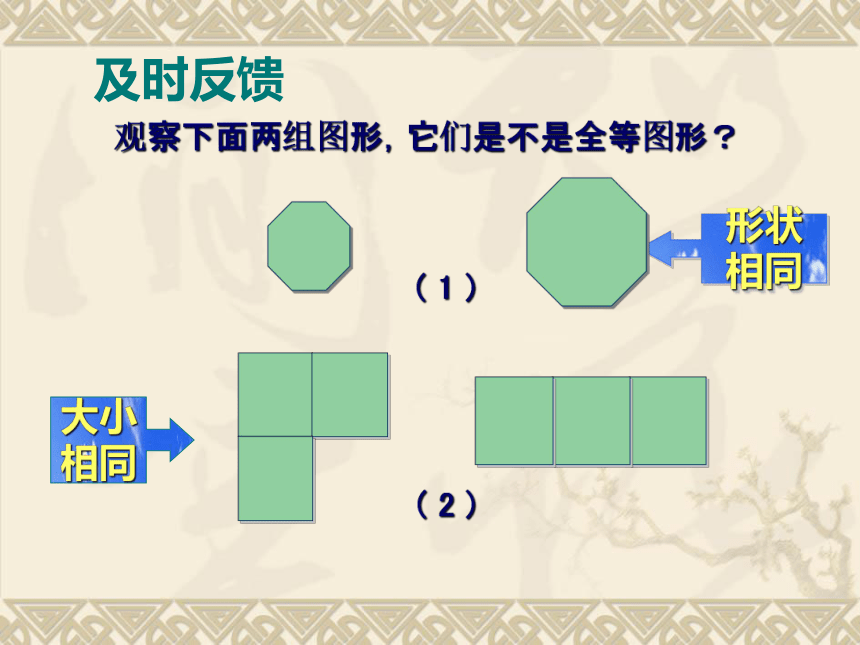
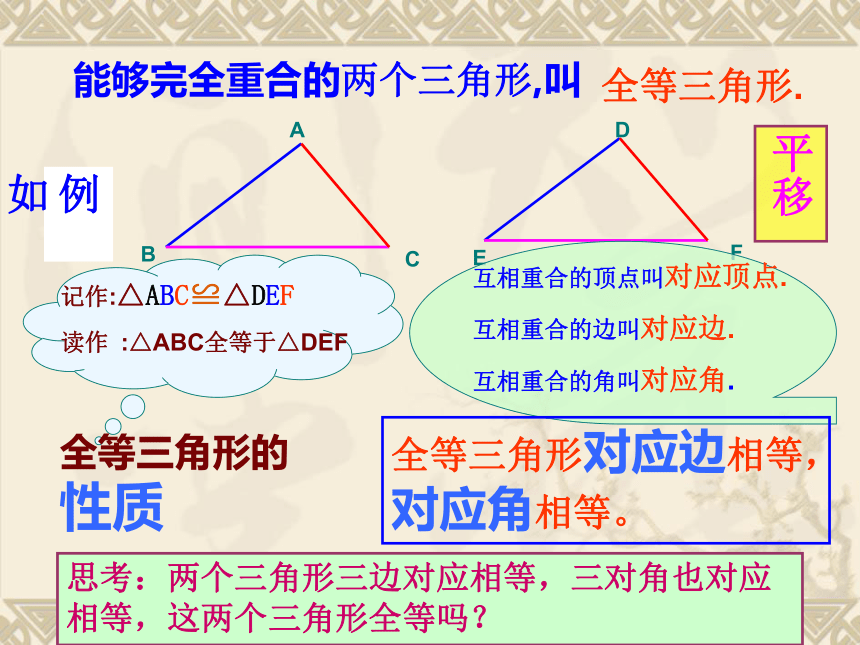
相同及时反馈例如能够完全重合的两个三角形,叫
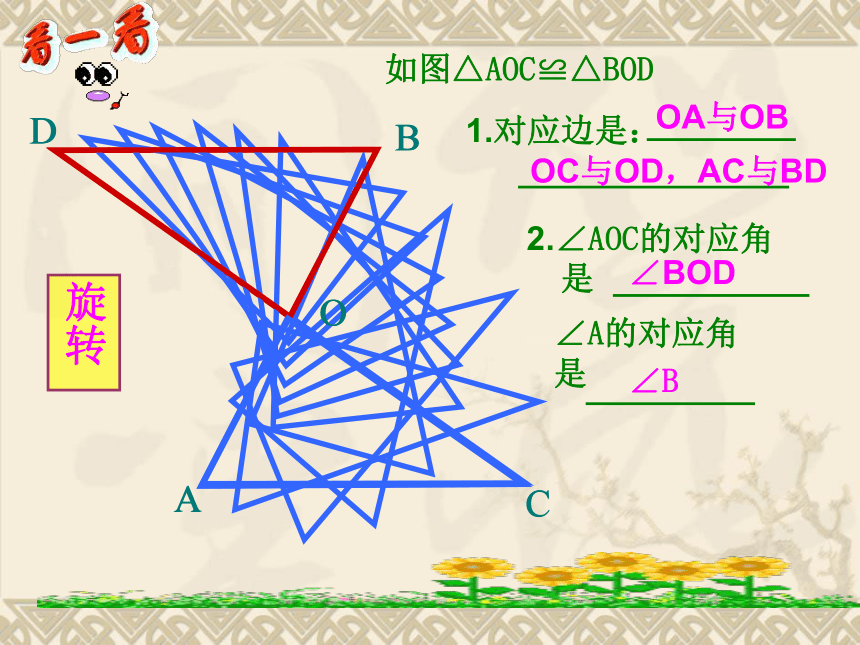
全等三角形.全等三角形对应边相等,对应角相等。全等三角形的性质平移思考:两个三角形三边对应相等,三对角也对应相等,这两个三角形全等吗?ACODB如图△AOC≌△BOD1.对应边是:2.∠AOC的对应角
是∠A的对应角
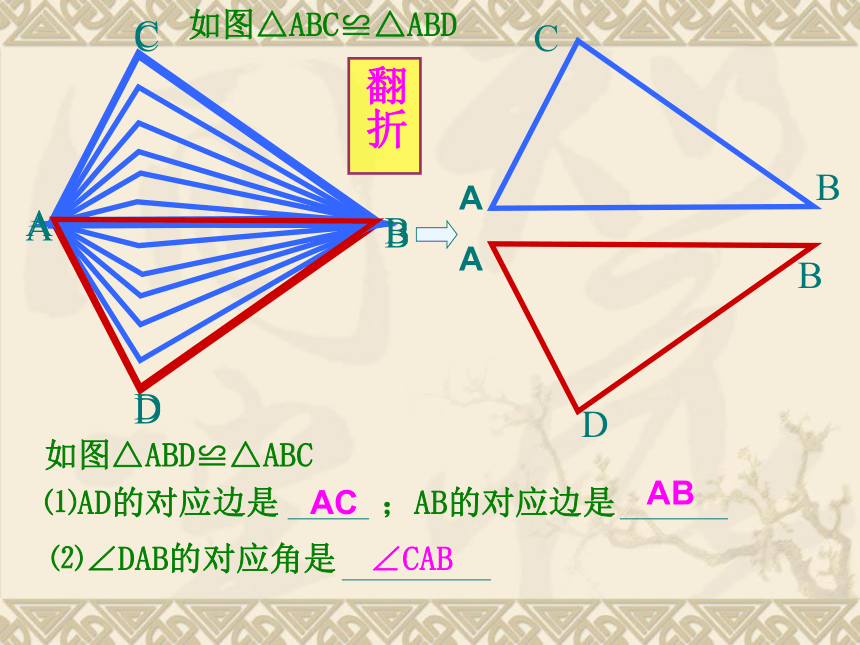
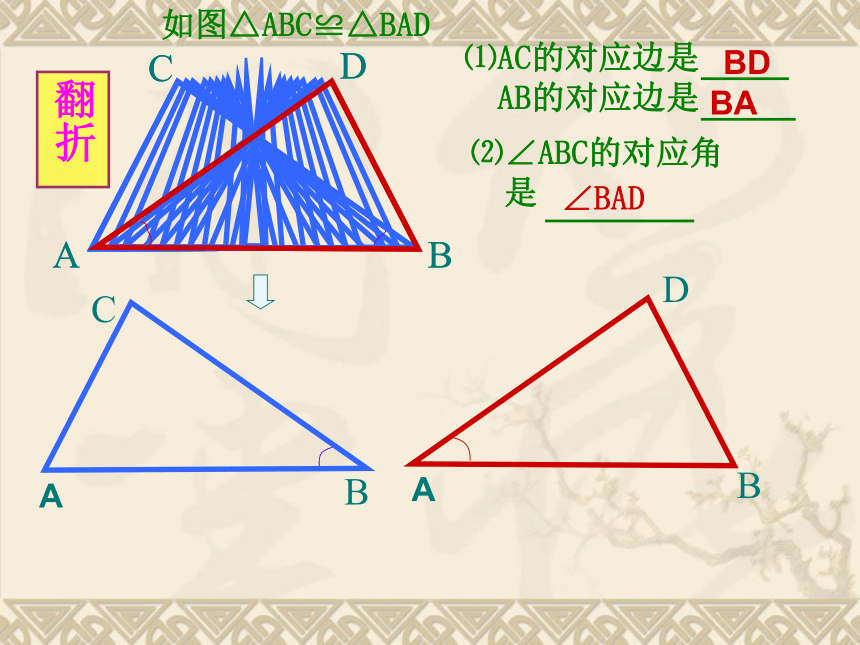
是OA与OBOC与OD,AC与BD∠BOD∠B旋转ABCDAABBDC如图△ABD≌△ABC⑴AD的对应边是 ;AB的对应边是⑵∠DAB的对应角是ACAB∠CAB翻折如图△ABC≌△ABDABBCDA⑴AC的对应边是
AB的对应边是⑵∠ABC的对应角
是BDBA∠BAD翻折如图△ABC≌△BADABCDE⑴△ ≌△⑵对应边是⑶对应角是ABCDECAC与DC,AB与DE,BC与EC∠A与∠D、∠B与∠E、∠ACB与∠DCE旋转有那些办法可以验证两个三角形全等?填一填:如图,已知△ABC≌△ADE,想一想: ∠ BAD= ∠ CAE吗?为什么?答:相等.理由如下:
∵△ABC≌△ADE(已知)
∴∠ BAC= ∠ DAE(全等三角形对应角相等)
∴∠ BAC - ∠ DAC= ∠ DAE - ∠ DAC(等式性质)
即∠ BAC= ∠ DAE对应顶点 :
对 应 边:
对 应 角:点A与点C、点B与点D、点C与点A.AB=CD、BC=DA、AC=CA、∠BAC =∠DCA 、∠B =∠C 、∠BCA= ∠DAC思考1:请同学们认真想一想:全等三角形的对应边与对应角之间有什么关系?已知全等表示:△ ≌ △ABCCDA写一写试一试
相信,你能行!找一找:请指出下列全等三角形的对应边和对应角1、 △ ABE ≌ △ ACF对应角是: ∠A和∠A、 ∠ABE和∠ACF、 ∠AEB和∠AFC;对应边是AB和AC、AE和AF、BE和CF。2、 △ BCE ≌ △ CBF对应角是: ∠BCE和 ∠CBF、 ∠BEC和∠CFB、 ∠CBE和 ∠BCF。对应边是:CB和BC、CE和BF、CF和BE。3、 △ BOF ≌ △ COE从以上学习中你能总结出找全等三角形的对应边,对应角的规律吗?提高2。如图已知△ AOC ≌ △BOD
求证:AC∥BD提高3。如图△ ABD ≌ △CDB,若AB=4,AD=5,BD=6,则BC= ,CD= 。提高4。如图△ABD≌ △EBC,AB=3cm,BC=5cm,求DE的长 1、全等用符号 表示,读作: 。 2、若△ BCE ≌ △ CBF,则∠CBE= , ∠BEC= ,BE= , CE= . 3、判断题 1)全等三角形的对应边相等,对应角相等。( ) 2)全等三角形的周长相等,面积也相等。 ( ) 3)面积相等的三角形是全等三角形。 ( ) 4)周长相等的三角形是全等三角形。 ( )≌全等于∠BCFCFBF∠CFB√ √ XX练习2如图:△ABC≌△DBF,找出图中的对应边,对应角.答:∠B的对应角是( )
∠C的对应角是( )
∠BAC的对应角是( )
AB的对应边是( )
AC的对应边是( )
BC的对应边是( )∠B∠F∠BDF DB DF BF 如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边, ∠BAC 与∠ EAD对应角,且∠BAC=25°, ∠B=35°,AB=3cm,BC=1cm,求出∠E, ∠ ADE的度数和线段DE,AE 的长度。练习3解:∵ △ABC≌△AED,(已知)∴∠E= ∠B= 35°(全等三角形对应角相等)∠ADE=∠ACB=18O°- 25°- 35°
=120 ° (全等三角形对应角相等)DE=BC=1cm, AE=AB=3cm
(全等三角形对应边相等)通过这节课的学习,你有什么收获?小结提高1、回忆这节课,学习了全等三角形的哪些知识?全等三角形的概念、性质、表示方法、对应写法等2、找全等三角形对应边、对应角的方法A、大边对应大边,大角对应大角B、公共边是对应边,公共角是对应角C、对应边所对的角是对应角,对应角 所对的边是对应边拓展与延伸下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?恭喜你,认真地学好了这节课! 作 业
能够完全重合的(1)(2)(3) 思考每组的两个图形有什么特点?观察能够重合,大小相同,形状相同能够完全重合的两个图形叫做全等形:全等图形的特征(1) 你还能说出生活中全等图形的例子吗? (2) 如果两个图形全等,它们的形状大小一定都相同吗?全等图形的形状和大小都相同形状
相同大小
相同及时反馈例如能够完全重合的两个三角形,叫
全等三角形.全等三角形对应边相等,对应角相等。全等三角形的性质平移思考:两个三角形三边对应相等,三对角也对应相等,这两个三角形全等吗?ACODB如图△AOC≌△BOD1.对应边是:2.∠AOC的对应角
是∠A的对应角
是OA与OBOC与OD,AC与BD∠BOD∠B旋转ABCDAABBDC如图△ABD≌△ABC⑴AD的对应边是 ;AB的对应边是⑵∠DAB的对应角是ACAB∠CAB翻折如图△ABC≌△ABDABBCDA⑴AC的对应边是
AB的对应边是⑵∠ABC的对应角
是BDBA∠BAD翻折如图△ABC≌△BADABCDE⑴△ ≌△⑵对应边是⑶对应角是ABCDECAC与DC,AB与DE,BC与EC∠A与∠D、∠B与∠E、∠ACB与∠DCE旋转有那些办法可以验证两个三角形全等?填一填:如图,已知△ABC≌△ADE,想一想: ∠ BAD= ∠ CAE吗?为什么?答:相等.理由如下:
∵△ABC≌△ADE(已知)
∴∠ BAC= ∠ DAE(全等三角形对应角相等)
∴∠ BAC - ∠ DAC= ∠ DAE - ∠ DAC(等式性质)
即∠ BAC= ∠ DAE对应顶点 :
对 应 边:
对 应 角:点A与点C、点B与点D、点C与点A.AB=CD、BC=DA、AC=CA、∠BAC =∠DCA 、∠B =∠C 、∠BCA= ∠DAC思考1:请同学们认真想一想:全等三角形的对应边与对应角之间有什么关系?已知全等表示:△ ≌ △ABCCDA写一写试一试
相信,你能行!找一找:请指出下列全等三角形的对应边和对应角1、 △ ABE ≌ △ ACF对应角是: ∠A和∠A、 ∠ABE和∠ACF、 ∠AEB和∠AFC;对应边是AB和AC、AE和AF、BE和CF。2、 △ BCE ≌ △ CBF对应角是: ∠BCE和 ∠CBF、 ∠BEC和∠CFB、 ∠CBE和 ∠BCF。对应边是:CB和BC、CE和BF、CF和BE。3、 △ BOF ≌ △ COE从以上学习中你能总结出找全等三角形的对应边,对应角的规律吗?提高2。如图已知△ AOC ≌ △BOD
求证:AC∥BD提高3。如图△ ABD ≌ △CDB,若AB=4,AD=5,BD=6,则BC= ,CD= 。提高4。如图△ABD≌ △EBC,AB=3cm,BC=5cm,求DE的长 1、全等用符号 表示,读作: 。 2、若△ BCE ≌ △ CBF,则∠CBE= , ∠BEC= ,BE= , CE= . 3、判断题 1)全等三角形的对应边相等,对应角相等。( ) 2)全等三角形的周长相等,面积也相等。 ( ) 3)面积相等的三角形是全等三角形。 ( ) 4)周长相等的三角形是全等三角形。 ( )≌全等于∠BCFCFBF∠CFB√ √ XX练习2如图:△ABC≌△DBF,找出图中的对应边,对应角.答:∠B的对应角是( )
∠C的对应角是( )
∠BAC的对应角是( )
AB的对应边是( )
AC的对应边是( )
BC的对应边是( )∠B∠F∠BDF DB DF BF 如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边, ∠BAC 与∠ EAD对应角,且∠BAC=25°, ∠B=35°,AB=3cm,BC=1cm,求出∠E, ∠ ADE的度数和线段DE,AE 的长度。练习3解:∵ △ABC≌△AED,(已知)∴∠E= ∠B= 35°(全等三角形对应角相等)∠ADE=∠ACB=18O°- 25°- 35°
=120 ° (全等三角形对应角相等)DE=BC=1cm, AE=AB=3cm
(全等三角形对应边相等)通过这节课的学习,你有什么收获?小结提高1、回忆这节课,学习了全等三角形的哪些知识?全等三角形的概念、性质、表示方法、对应写法等2、找全等三角形对应边、对应角的方法A、大边对应大边,大角对应大角B、公共边是对应边,公共角是对应角C、对应边所对的角是对应角,对应角 所对的边是对应边拓展与延伸下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?恭喜你,认真地学好了这节课! 作 业
