分数乘除法——倒数与比和比例-六年级上册数学人教版(课件)(共32张PPT)
文档属性
| 名称 | 分数乘除法——倒数与比和比例-六年级上册数学人教版(课件)(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 635.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-28 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
人教版小学数学
分数乘除法
------倒数与比和比例
倒数与比和比例
根据男女生人数,你可以想到几个比?
1.先计算,再观察,看看有什么规律。
乘积是 1 的两个数互为倒数。
=
3
8
8
3
=
7
15
15
7
=
5
1
5
=
12
12
1
×
×
×
×
合作归纳
2.说出下列各数的倒数。
的倒数是( ) 。
⑴
的倒数是( ) 。
⑵
的倒数是( ) 。
⑷
的倒数是( ) 。
⑸
的倒数是( ) 。
⑶
的倒数是( ) 。
⑹
3.先说出每组数的倒数,再说一说你发现了什么规律
⑴
真分数的倒数一定大于 1 。
大于 1 的假分数的倒数一定小于 1 。
不为 0 的整数,它的 倒数的分子一定是 1 。
⑵
⑷
⑶
分子是 1 的分数,它的倒数一定是整数 。
0 ×( 任何数 ) ≠1
0 没有倒数,因为0作分母没有意义。
1的倒数是多少?
0有倒数吗,为什么?
合作归纳
联 系
例子
各部分名称
分数
除法
比
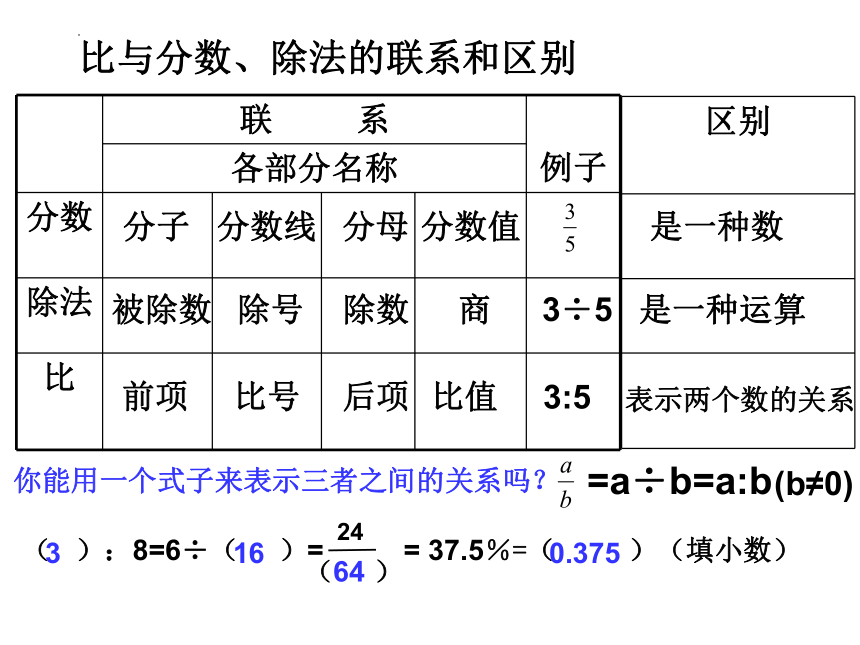
比与分数、除法的联系和区别
你能用一个式子来表示三者之间的关系吗?
=a÷b=a:b
分子
分数线
分母
分数值
商
前项
比号
后项
比值
区别
3÷5
3:5
是一种数
是一种运算
表示两个数的关系
被除数
除号
除数
(b≠0)
( ):8=6÷( )= = 37.5%=( )(填小数)
24
( )
3
16
64
0.375
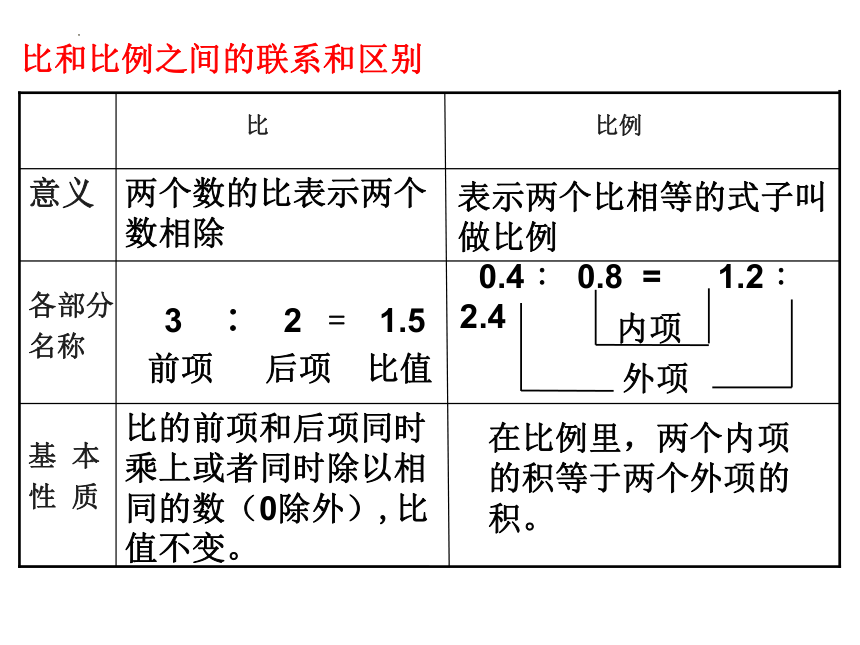
在比例里,两个内项的积等于两个外项的积。
比的前项和后项同时乘上或者同时除以相同的数(0除外),比值不变。
基 本
性 质
3 ∶ 2 = 1.5
前项 后项 比值
各部分
名称
表示两个比相等的式子叫做比例
两个数的比表示两个数相除
意义
比例
比
内项
外项
0.4 ∶ 0.8 = 1.2 ∶ 2.4
比和比例之间的联系和区别
15÷10
10÷15
42252÷90
两个数相除又叫做两个数的比。
可以写成:
可以写成:
可以写成:
15:10
10:15
42252:90
合作归纳
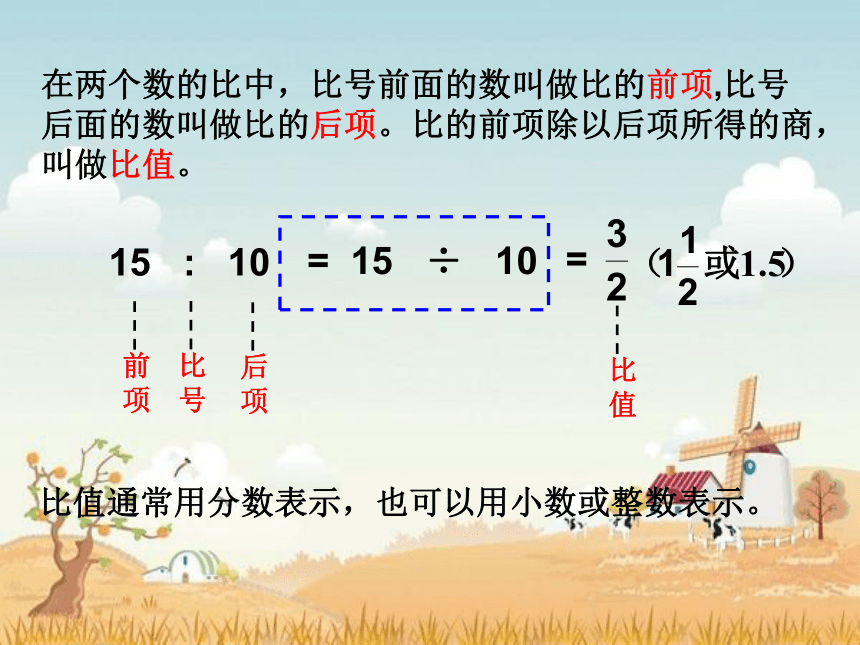
在两个数的比中,比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。
比值通常用分数表示,也可以用小数或整数表示。
前
项
比
号
后
项
比值
15 : 10
= 15 ÷ 10
=
根据分数与除法的关系,两个数的比也可以写成分数的形式。例如:
15 : 10也可以写成 ,仍读作:“15比10”。
合作归纳
如何判断两种相关联的量是否成正、反比例关系?
可以举例说明
1、全班人数一定,出勤人数与缺勤人数。
2、已知 y =3x(xy均不为0),y与x。
3、三角形的面积一定,它的底和高。
4、出油率一定,花生油的质量与花生的质量。
不成比例
成正比例关系
成正比例关系
成反比例关系
练一练
查缺补漏我能行
3.如果6a=10b(a、b≠0),那么a:b=( )。
练一练
查缺补漏我能行
2.做一个工程,甲需要6天,乙需要8天,甲和乙的工作效率比是( )。
4:3
1.把一只5毫米的蚂蚁画在纸上是20厘米,它的比例尺是( )
40:1
小试牛刀
练一练
2、用一根长96厘米的铁丝焊成一个长方体框架,使长方体的长、宽、高的比是5:4:3。这个长方体的体积是多少?
你能编一道同类型的数学问题吗?
1、男生和女生的比是4:5,女生比男生多6人,全班共有多少人?
练一练
2、一间教室,用面积是16平方分米的方砖铺地,需要50块,如果改用边长为5分米的方砖铺,需要几块?(用比例解)
智力大比拼
1、一辆客车3小时行驶240千米,照这样的速度,行驶400千米需要多少小时?(用比例解决)
1.小强的身高1米,他爸爸的身高是173厘米,小强说他和他爸爸的身高比是1 ︰ 173,对不对?如果不对,你认为是多少呢?
合作归纳
3.判断:
(1)六年级小刚的跳远成绩是2米,三年级的小明的跳远成绩是110厘米,他们的成绩比是2:110。 ( )
(2)1500米长跑,王成用6分,张静用8分钟,他俩的速度比是6:8 ( )
合作归纳
(3)大卡车的载重量是5吨,小卡车的载重量是2吨,大小卡车载重量的比是 。( )
(4)如果A是B的3倍,那么A与B的比是1﹕3。( )
合作归纳
(5) 既可以读作十五分之七,又可以读作七比十五。( )
(6)把1克盐溶于20克水中,盐与盐水重量的比是1:20。( )
合作归纳
3 :( )= 24
( ): 8 = 0.5
4
后项=前项÷比值
前项=后项×比值
比值=前项÷后项
4.填空
合作归纳
比的前项和后项同时乘或除以相同的数(0除外),比值不变。这叫做比的基本性质。
利用商不变性质,我们可以进行除法的简算。
根据分数的基本性质,我们可以把分数约分成最简分数。
应用比的基本性质,我们可以把比化成最简单的整数比。
怎样化解整数比?
比的前、后项都除以它们的最大公因数→最简比。
32 : 16
48 : 40
0.75︰2
0.15 : 0.3
化简下列各比。
合作归纳
归纳化简比的方法:
(1) 整数比
(2) 小数比
(3) 分数比
——比的前、后项都除以它们的最大公因数→最简比。
——比的前、后项都扩大相同的倍数→整数比→最简比。
——比的前、后项都乘它们分母的最小公倍数→整数比→最简比。
6、 生产一批零件,甲单独做6小时完成,乙单独做8小时完成。
(1)、甲完成任务的时间与乙完成任务的时间
的最简比是( ) ︰ ( )
(2)、甲的工作效率与乙的工作效率的最简比
是( ) ︰ ( )
(3)、乙的工作效率与甲的工作效率的最简比
是( ) ︰ ( )
合作归纳
化简比和求比值的区别
求比值 化简比
意义
方法
结果
比的前项除以
后项所得的商
把一个比化成最简单的整数比的过程
是一个比
是一个数
前项÷后项
前、后项同时乘或
除以一个不为0的数
比 最简单的整数比 比值
25 ∶100
∶
4.2∶1.4
求比值和化简比:
(1)把空气平均分成的份数:21+78 =99
(2)氧气的体积:
(3)氮气的体积:
答:有氧气140立方米,有氮气520立方米。
合作归纳
合作归纳
合作归纳
已知总数和各部分数的比,求各部分数。
1、根据比先求出总份数。
2、求出各部分数占总数的几分之几。
3、运用分数乘法列式计算,求出各部分数。
4、答题并检验。
按比例分配应用题的结构特征:
方法和步骤:
说说你这节课的收获。
还有哪里不明白吗?
人教版小学数学
分数乘除法
------倒数与比和比例
倒数与比和比例
根据男女生人数,你可以想到几个比?
1.先计算,再观察,看看有什么规律。
乘积是 1 的两个数互为倒数。
=
3
8
8
3
=
7
15
15
7
=
5
1
5
=
12
12
1
×
×
×
×
合作归纳
2.说出下列各数的倒数。
的倒数是( ) 。
⑴
的倒数是( ) 。
⑵
的倒数是( ) 。
⑷
的倒数是( ) 。
⑸
的倒数是( ) 。
⑶
的倒数是( ) 。
⑹
3.先说出每组数的倒数,再说一说你发现了什么规律
⑴
真分数的倒数一定大于 1 。
大于 1 的假分数的倒数一定小于 1 。
不为 0 的整数,它的 倒数的分子一定是 1 。
⑵
⑷
⑶
分子是 1 的分数,它的倒数一定是整数 。
0 ×( 任何数 ) ≠1
0 没有倒数,因为0作分母没有意义。
1的倒数是多少?
0有倒数吗,为什么?
合作归纳
联 系
例子
各部分名称
分数
除法
比
比与分数、除法的联系和区别
你能用一个式子来表示三者之间的关系吗?
=a÷b=a:b
分子
分数线
分母
分数值
商
前项
比号
后项
比值
区别
3÷5
3:5
是一种数
是一种运算
表示两个数的关系
被除数
除号
除数
(b≠0)
( ):8=6÷( )= = 37.5%=( )(填小数)
24
( )
3
16
64
0.375
在比例里,两个内项的积等于两个外项的积。
比的前项和后项同时乘上或者同时除以相同的数(0除外),比值不变。
基 本
性 质
3 ∶ 2 = 1.5
前项 后项 比值
各部分
名称
表示两个比相等的式子叫做比例
两个数的比表示两个数相除
意义
比例
比
内项
外项
0.4 ∶ 0.8 = 1.2 ∶ 2.4
比和比例之间的联系和区别
15÷10
10÷15
42252÷90
两个数相除又叫做两个数的比。
可以写成:
可以写成:
可以写成:
15:10
10:15
42252:90
合作归纳
在两个数的比中,比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。
比值通常用分数表示,也可以用小数或整数表示。
前
项
比
号
后
项
比值
15 : 10
= 15 ÷ 10
=
根据分数与除法的关系,两个数的比也可以写成分数的形式。例如:
15 : 10也可以写成 ,仍读作:“15比10”。
合作归纳
如何判断两种相关联的量是否成正、反比例关系?
可以举例说明
1、全班人数一定,出勤人数与缺勤人数。
2、已知 y =3x(xy均不为0),y与x。
3、三角形的面积一定,它的底和高。
4、出油率一定,花生油的质量与花生的质量。
不成比例
成正比例关系
成正比例关系
成反比例关系
练一练
查缺补漏我能行
3.如果6a=10b(a、b≠0),那么a:b=( )。
练一练
查缺补漏我能行
2.做一个工程,甲需要6天,乙需要8天,甲和乙的工作效率比是( )。
4:3
1.把一只5毫米的蚂蚁画在纸上是20厘米,它的比例尺是( )
40:1
小试牛刀
练一练
2、用一根长96厘米的铁丝焊成一个长方体框架,使长方体的长、宽、高的比是5:4:3。这个长方体的体积是多少?
你能编一道同类型的数学问题吗?
1、男生和女生的比是4:5,女生比男生多6人,全班共有多少人?
练一练
2、一间教室,用面积是16平方分米的方砖铺地,需要50块,如果改用边长为5分米的方砖铺,需要几块?(用比例解)
智力大比拼
1、一辆客车3小时行驶240千米,照这样的速度,行驶400千米需要多少小时?(用比例解决)
1.小强的身高1米,他爸爸的身高是173厘米,小强说他和他爸爸的身高比是1 ︰ 173,对不对?如果不对,你认为是多少呢?
合作归纳
3.判断:
(1)六年级小刚的跳远成绩是2米,三年级的小明的跳远成绩是110厘米,他们的成绩比是2:110。 ( )
(2)1500米长跑,王成用6分,张静用8分钟,他俩的速度比是6:8 ( )
合作归纳
(3)大卡车的载重量是5吨,小卡车的载重量是2吨,大小卡车载重量的比是 。( )
(4)如果A是B的3倍,那么A与B的比是1﹕3。( )
合作归纳
(5) 既可以读作十五分之七,又可以读作七比十五。( )
(6)把1克盐溶于20克水中,盐与盐水重量的比是1:20。( )
合作归纳
3 :( )= 24
( ): 8 = 0.5
4
后项=前项÷比值
前项=后项×比值
比值=前项÷后项
4.填空
合作归纳
比的前项和后项同时乘或除以相同的数(0除外),比值不变。这叫做比的基本性质。
利用商不变性质,我们可以进行除法的简算。
根据分数的基本性质,我们可以把分数约分成最简分数。
应用比的基本性质,我们可以把比化成最简单的整数比。
怎样化解整数比?
比的前、后项都除以它们的最大公因数→最简比。
32 : 16
48 : 40
0.75︰2
0.15 : 0.3
化简下列各比。
合作归纳
归纳化简比的方法:
(1) 整数比
(2) 小数比
(3) 分数比
——比的前、后项都除以它们的最大公因数→最简比。
——比的前、后项都扩大相同的倍数→整数比→最简比。
——比的前、后项都乘它们分母的最小公倍数→整数比→最简比。
6、 生产一批零件,甲单独做6小时完成,乙单独做8小时完成。
(1)、甲完成任务的时间与乙完成任务的时间
的最简比是( ) ︰ ( )
(2)、甲的工作效率与乙的工作效率的最简比
是( ) ︰ ( )
(3)、乙的工作效率与甲的工作效率的最简比
是( ) ︰ ( )
合作归纳
化简比和求比值的区别
求比值 化简比
意义
方法
结果
比的前项除以
后项所得的商
把一个比化成最简单的整数比的过程
是一个比
是一个数
前项÷后项
前、后项同时乘或
除以一个不为0的数
比 最简单的整数比 比值
25 ∶100
∶
4.2∶1.4
求比值和化简比:
(1)把空气平均分成的份数:21+78 =99
(2)氧气的体积:
(3)氮气的体积:
答:有氧气140立方米,有氮气520立方米。
合作归纳
合作归纳
合作归纳
已知总数和各部分数的比,求各部分数。
1、根据比先求出总份数。
2、求出各部分数占总数的几分之几。
3、运用分数乘法列式计算,求出各部分数。
4、答题并检验。
按比例分配应用题的结构特征:
方法和步骤:
说说你这节课的收获。
还有哪里不明白吗?
