2022-2023学年河北省沧州市盐山县七年级(下)期末数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年河北省沧州市盐山县七年级(下)期末数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 301.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-28 20:48:13 | ||
图片预览



文档简介
2022-2023学年河北省沧州市盐山县七年级(下)期末数学试卷
一、选择题(本大题共16小题,共42.0分。在每小题列出的选项中,选出符合题目的一项)
1. 如图所示,已知,下列结论正确的是( )
A.
B.
C.
D.
2. 下列命题:过一点有且只有一条直线与已知直线平行;过一点有且只有一条直线与已知直线垂直;同旁内角互补;垂直于同一条直线的两条直线垂直其中的假命题有( )
A. 个 B. 个 C. 个 D. 个
3. 若一个数的平方根是,则这个数的立方根是( )
A. B. C. D.
4. 在下列各数,,,,,两个之间,依次增加个,其中无理数有( )
A. 个 B. 个 C. 个 D. 个
5. 若点在第三象限,则点一定在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
6. 下列说法中,正确的是( )
的立方根是;
的算术平方根是;
的立方根是;
的平方根是.
A. 个 B. 个 C. 个 D. 个
7. 已知方程,用含的代数式表示( )
A. B. C. D.
8. 已知,则下列结论不成立的是( )
A. B. C. D.
9. 估计的值应在( )
A. 和之间 B. 和之间 C. 和之间 D. 和之间
10. 在平面直角坐标系中,已知线段的两个端点的坐标分别是、,将线段向上移动个单位,向左移动个单位平移后,点,的对应坐标为( )
A. , B. ,
C. , D. ,
11. 下列调查中,适合用全面调查的是( )
A. 调查某批次汽车的抗撞击能力
B. 调查春节联欢晚会的收视率
C. “神七”飞船发射前对重要零部件的检查
D. 调查市场上某种食品的色素含量是否符合国家标准
12. 如果关于的不等式的解集为,那么的取值范围是( )
A. B. C. D.
13. 下列说法正确的是( )
A. 点在第四象限
B. 若,则在坐标原点
C. 点在第二象限,且点到轴的距离为,点到轴的距离为,则点的坐标为
D. 在平面直角坐标系中,若点的坐标为,且平行于轴,,则点的坐标为
14. 把一堆练习本分给学生,如果每名学生分本,那么多本;如果每名学生分本,那么最后名学生只有本设有名学生,本书,根据题意,可列方程组为( )
A. B.
C. D.
15. 某次知识竞赛共有道题,答对一题得分,答错或不答均扣分,小玉得分超过分,他至少要答对道题.( )
A. B. C. D.
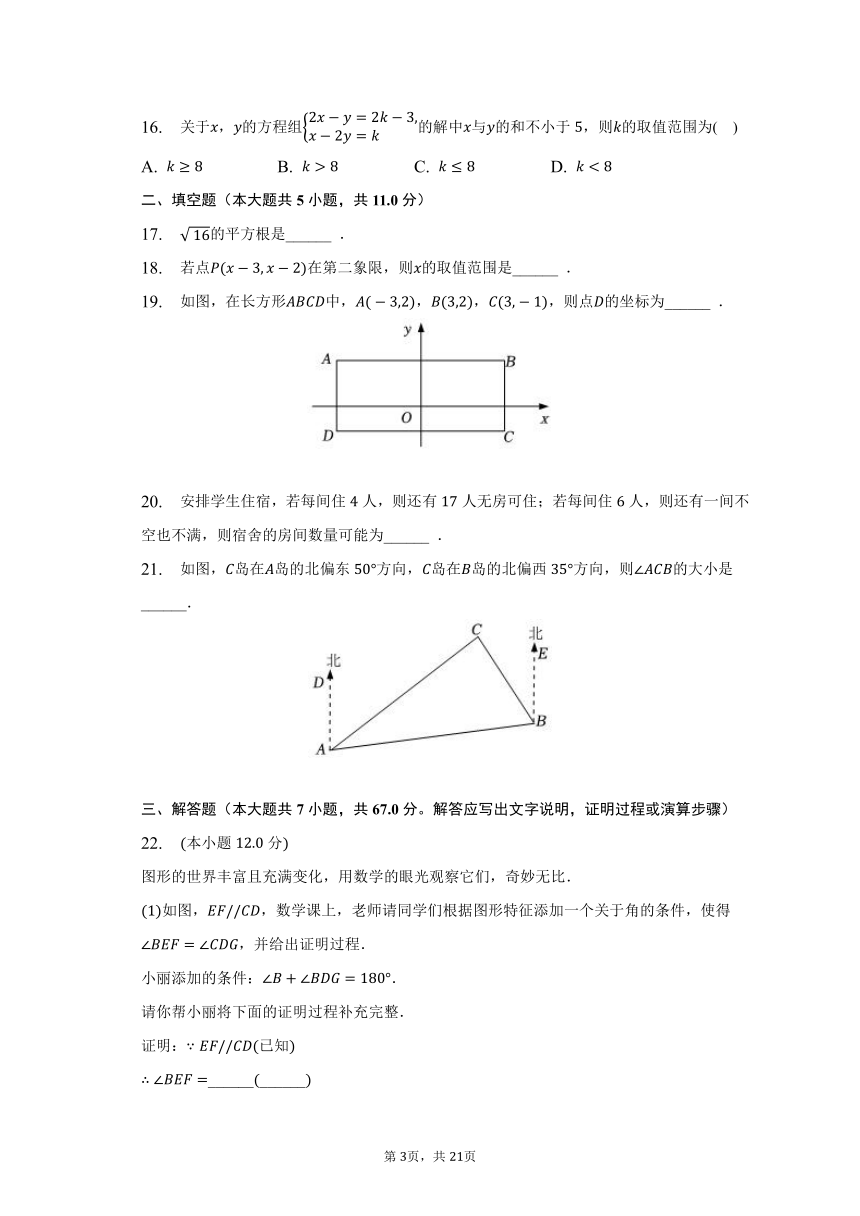
16. 关于,的方程组的解中与的和不小于,则的取值范围为( )
A. B. C. D.
二、填空题(本大题共5小题,共11.0分)
17. 的平方根是______ .
18. 若点在第二象限,则的取值范围是______ .
19. 如图,在长方形中,,,,则点的坐标为______ .
20. 安排学生住宿,若每间住人,则还有人无房可住;若每间住人,则还有一间不空也不满,则宿舍的房间数量可能为______ .
21. 如图,岛在岛的北偏东方向,岛在岛的北偏西方向,则的大小是______.
三、解答题(本大题共7小题,共67.0分。解答应写出文字说明,证明过程或演算步骤)
22. 本小题分
图形的世界丰富且充满变化,用数学的眼光观察它们,奇妙无比.
如图,,数学课上,老师请同学们根据图形特征添加一个关于角的条件,使得,并给出证明过程.
小丽添加的条件:.
请你帮小丽将下面的证明过程补充完整.
证明:已知
____________
已知
____________
____________
等量代换
拓展:如图,请你从三个选项,平分,中任选出两个作为条件,另一个作为结论,组成一个真命题,并加以证明.
条件:______,结论:______填序号.
证明:______.
23. 本小题分
解方程组;
解不等式组并在数轴上表示解集.
24. 本小题分
已知点,请分别根据下列条件,求出点的坐标.
点在轴上,则点坐标为______;
点的横坐标比纵坐标大;
点在过点且与轴平行的直线上.
25. 本小题分
已知正数的两个不等的平方根分别是和,的立方根为;是的整数部分;求的平方根.
26. 本小题分
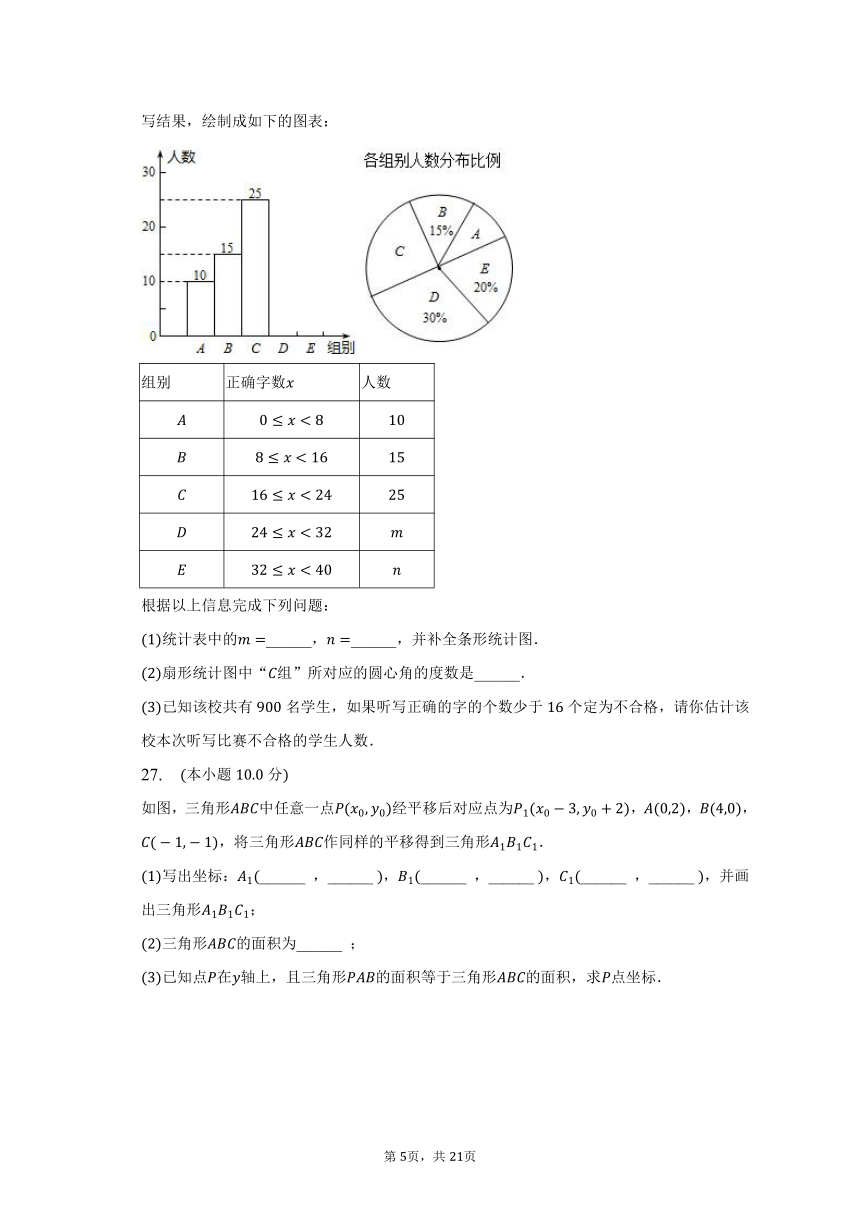
某校举行全体学生“汉字听写”比赛,每位学生听写汉字个.现随机抽取了部分学生的听写结果,绘制成如下的图表:
组别 正确字数 人数
根据以上信息完成下列问题:
统计表中的______,______,并补全条形统计图.
扇形统计图中“组”所对应的圆心角的度数是______.
已知该校共有名学生,如果听写正确的字的个数少于个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
27. 本小题分
如图,三角形中任意一点经平移后对应点为,,,,将三角形作同样的平移得到三角形.
写出坐标:______ ,______ ,______ ,______ ,______ ,______ ,并画出三角形;
三角形的面积为______ ;
已知点在轴上,且三角形的面积等于三角形的面积,求点坐标.
28. 本小题分
学校开展大课间活动,某班需要购买、两种跳绳.已知购进根种跳绳和根种跳绳共需元:购进根种跳绳和根种跳绳共需元.
求购进一根种跳绳和一根种跳绳各需多少元?
设购买种跳绳根,若班级计划购买、两种跳绳共根,所花费用不少于元且不多于元,则有哪几种购买方案?
在的条件下,哪种购买方案需要的总费用最少?最少费用是多少元?
答案和解析
1.【答案】
【解析】解:,
,
故选:.
根据平行线的性质即可得到结论.
本题考查了平行线的性质,熟练掌握两直线平行,同位角相等是解题的关键.
2.【答案】
【解析】解:过直线外一点有且只有一条直线与已知直线平行,故原命题错误,是假命题;
过直线外一点有且只有一条直线与已知直线垂直,故原命题错误,是假命题;
两直线平行,同旁内角互补,故原命题错误,是假命题;
平面内垂直于同一条直线的两条直线平行,故原命题错误,是假命题.
假命题有个,
故选:.
利用平行公理及有关平面内两直线的位置关系分别判断后即可确定正确的选项.
本题考查了命题与定理的知识,解题的关键是了解平行线的性质及平行公理等知识,难度不大.
3.【答案】
【解析】解:一个数的平方根是,
这个数为,
故的立方根是.
故选:.
首先利用平方根的定义求出这个数,然后根据立方根的定义即可求解.
此题主要考查了立方根的定义,求一个数的立方根,应先找出所要求的这个数是哪一个数的立方.由开立方和立方是互逆运算,用立方的方法求这个数的立方根.注意一个数的立方根与原数的性质符号相同.
4.【答案】
【解析】解:,
,,是有理数,
,,两个之间,依次增加个是无理数,
无理数有个,
故选:.
根据无理数、有理数的定义解答即可.
此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如,,每两个之间依次多个等形式.
5.【答案】
【解析】解:点在第三象限,
,,
,,
点一定在第二象限.
故选:.
根据第三象限的点的坐标特征求出、的正负情况,然后判断出点所在的象限即可.
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解题的关键,四个象限的符号特点分别是:第一象限,第二象限,第三象限,第四象限.
6.【答案】
【解析】解:的立方根是,原说法正确;
的算术平方根是,原说法错误;
的立方根是,原说法正确;
的平方根是,原说法错误;
正确的个数有个;
故选:.
根据立方根、平方根和算术平方根的定义分别对每小题进行分析,即可得出答案.
此题考查了立方根、平方根和算术平方根,熟练掌握立方根、平方根和算术平方根的定义是解题的关键.
7.【答案】
【解析】解:,
移项、得.
故选:.
把含的项放到方程左边,移项即可.
本题考查的是方程的基本运算技能:移项、合并同类项、系数化为等,表示谁就该把谁放到等号的一边,其他的项移到另一边,然后合并同类项、系数化就可用含的式子表示的形式.
8.【答案】
【解析】解:、由,可得,成立;
B、由,可得,不成立;
C、由,可得,成立;
D、由,可得,成立;
故选:.
根据不等式的性质解答即可.
此题考查不等式的性质,关键是根据不等式的性质解答.
9.【答案】
【解析】解:,
,
故选:.
直接利用平方数可知,从而估算无理数的大小.
此题主要考查了估算无理数的大小,正确估算无理数是解题关键.
10.【答案】
【解析】解:线段向上移动个单位,向左移动个单位平移,
平移后、对应坐标为、,
即,.
故选:.
根据将线段向上移动个单位,向左移动个单位平移,纵坐标加,横坐标减,从而得出答案.
本题考查图形的平移变换,关键是要懂得左右平移点的纵坐标不变,而上下平移时点的横坐标不变,平移变换是中考的常考点.比较对应点的坐标变化,寻找变化规律,并把变化规律运用到其它对应点上.
11.【答案】
【解析】解:、调查某批次汽车的抗撞击能力,具有破坏性,适合采用抽样调查,故本选项不合题意;
B、调查春节联欢晚会的收视率,范围广,人数多,适合采用抽样调查,故本选项不符合题意;
C、“神七”飞船发射前对重要零部件的检查,涉及安全性,适合采用全面调查,故本选项符合题意;
D、调查市场上某种食品的色素含量是否符合国家标准,范围广,适合采用抽样调查,故本选项不合题意.
故选:.
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
12.【答案】
【解析】解:不等式的解集为,
,
故选:.
运用不等式的基本性质求解即可.
本题考查了不等式的基本性质,解题的关键是熟记不等式的基本性质.
13.【答案】
【解析】
【分析】
本题主要考查了坐标与图形性质,熟练掌握坐标与图形性质进行求解是解决本题的关键.
应用坐标与图形性质进行判定即可得出答案.
【解答】
解:因为当时,点在轴上,所以选项说法不一定正确,故A选项不符合题意;
B.因为当,,或,时,,则在轴或轴上,不一定在坐标原点,所以选项说法不一定正确,故B选项不符合题意;
C.因为点在第二象限,且点到轴的距离为,点到轴的距离为,则点的坐标为,所以选项说法正确,故C选项符合题意;
D.因为在平面直角坐标系中,若点的坐标为,且平行于轴,,则点的坐标为或,所以选项说法正确,故D选项不符合题意.
故选:.
14.【答案】
【解析】解:依题意,得:.
故选:.
根据“如果每名学生分本,那么多本;如果每名学生分本,那么最后名学生只有本”,即可得出关于,的二元一次方程组,此题得解.
本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
15.【答案】
【解析】解:设小玉答对了道题,
解得,
小玉至少答对道,
故选:.
根据题意可以列出相应的不等式,从而可以求得的取值范围,由于是整数,从而可以解答本题.
本题考查一元一次不等式的应用,解题的关键是明确题意,列出相应的一元一次不等式.
16.【答案】
【解析】解:把两个方程相减,可得,
根据题意得:,
解得:.
所以的取值范围是.
故选:.
两个方程相减可得出,根据列出关于的不等式,解之可得答案.
本题主要考查解一元一次不等式,解二元一次方程组,解题的关键是掌握解一元一次不等式的能力、不等式的基本性质等知识点.
17.【答案】
【解析】解:,
的平方根是.
故答案为:.
如果一个数的平方等于,这个数就叫做的平方根,如果一个正数的平方等于,即,那么这个正数叫做的算术平方根.记为,由此即可得到答案.
本题考查平方根、算术平方根,关键是掌握平方根、算术平方根的定义.
18.【答案】
【解析】解:由题意可得:,
解得:.
故答案为:.
根据第二象限的点的特征,列出不等式组,解之即可.
本题考查了解一元一次不等式组,掌握各象限点的坐标特征是解题关键.
19.【答案】
【解析】解:,,
,轴,
四边形是长方形,
,轴,
同理可得轴,
点,
点的坐标为,
故答案为:.
先根据、的坐标求出的长,则,并证明轴,同理可得轴,由此即可得到答案.
本题主要考查了坐标与图形,熟知长方形的性质是解题的关键.
20.【答案】或或或
【解析】解:设共有间宿舍,则共有个学生,
依题意得:,
解得:.
又为正整数,
或或或.
故答案为:或或或.
设共有间宿舍,则共有个学生,然后根据每间住人,则还有一间不空也不满,列出不等式组进行求解即可.
本题主要考查了一元一次不等式组的应用,解题的关键在于能够准确根据题意列出不等式组进行求解.
21.【答案】
【解析】解:过点作,如图,
,
,
,,
,
由岛在岛的北偏东方向,岛在岛的北偏西方向,得
,.
,
故答案为:.
过点作,根据平行线的性质,求得与,再由角的和差可得答案.
本题考查了方向角,平行线的性质,利用平行线的性质得出得出,是解题关键.
22.【答案】;两直线平行,同位角相等;;同旁内角互补,两直线平行;;两直线平行,内错角相等;
;;答案不唯一
,
,,
,
,即平分.
【解析】证明:已知,
两直线平行,同位角相等,
已知,
同旁内角互补,两直线平行,
两直线平行,内错角相等,
等量代换;
故答案为;两直线平行,同位角相等;;同旁内角互补,两直线平行;;两直线平行,内错角相等;
条件:,,
结论:平分,
证明:,
,,
,
,即平分.
故答案为;;答案不唯一
,
,,
,
,即平分.
根据平行线的判定定理和性质定理解答;
根据真命题的概念写出命题的条件和结论,根据平行线的判定定理和性质定理、角平分线的定义解答.
本题考查的是命题的真假判断、平行线的判定和性质,掌握平行线的判定定理和性质定理是解题的关键.
23.【答案】解:,
得:,
解得,
把代入得:,
解得,
方程组的解为;
,
解不等式得:,
解不等式得:,
不等式组无解,
数轴表示如下:
【解析】利用加减消元法解二元一次方程组即可;
按照解一元一次不等式组的步骤,先求出两个不等式的解集,然后再求出不等式组的解集,最后在数轴上表示出不等式组的解集即可.
本题主要考查了解二元一次方程组,解一元一次不等式组,熟知相关计算方法是解题的关键.
24.【答案】解:;
点的横坐标比纵坐标大,
,
,
,,
点坐标为;
点在过点且与轴平行的直线上,
点的横坐标为,
,
,
,
点坐标为.
【解析】解:点在轴上,
,
,
,
点坐标为,
故答案为:;
点的横坐标比纵坐标大,
,
,
,,
点坐标为;
点在过点且与轴平行的直线上,
点的横坐标为,
,
,
,
点坐标为.
直接利用轴上点的坐标特点求出的值,即可求出点的坐标;
利用点的横坐标比纵坐标大求出的值,即可求出点的坐标;
利用点在过点且与轴平行的直线上,横坐标相同出的值,即可求出点的坐标.
本题考查了坐标与图形的性质,正确分析各点的坐标特点是解决问题的关键.
25.【答案】解:正数的两个不等的平方根分别是和,
,
解得:,
的立方根为,
,
解得:,
是的整数部分,
,
,
的平方根是.
【解析】根据平方根定义、立方根定义和无理数的估算求出、、的值,然后再求出的值即可得出答案.
本题主要考查了平方根、立方根和无理数的估算,解题的关键是求出,,.
26.【答案】解:;;
补全条形统计图如下:
;
估计这所学校本次听写比赛不合格的
学生人数为:
人.
【解析】
【分析】
本题考查的是频数分布表、条形图和扇形图的知识,利用统计图获取正确信息是解题的关键.注意频数、频率和样本容量之间的关系的应用.
根据条形图和扇形图确定组的人数所占的百分比求出样本容量,求出、的值;
求出组”所占的百分比,得到所对应的圆心角的度数;
求出不合格人数所占的百分比,求出该校本次听写比赛不合格的学生人数.
【解答】
解:从条形图可知,组有人,
从扇形图可知,组所占的百分比是,组所占的百分比是,组所占的百分比是,
,
,
,
,;
补全条形统计图如图;
故答案为;
“组”所对应的圆心角的度数是;
故答案为;
见答案.
27.【答案】
【解析】解:,,;如图,为所作;
三角形的面积;
故答案为,;,;,;;
设,
三角形的面积等于三角形的面积,
,解得,,
点坐标为或
利用点和的坐标特征确定平移的规律,然后写出、、的坐标,再描点即可;
用一个矩形的面积分别减去三个直角三角形的面积去计算三角形的面积;
设,利用三角形面积公式得,然后解方程求出,从而得到点坐标.
本题考查了作图平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
28.【答案】解:设购进一根种跳绳需元,购进一根种跳绳需元,
依题意得:,
解得:.
答:购进一根种跳绳需元,购进一根种跳绳需元.
该班级计划购买、两种跳绳共根,且购买种跳绳根,
购买种跳绳根.
依题意得:,
解得:,
又为整数,
可以取,,,
共有种购买方案,
方案:购买根种跳绳,根种跳绳;
方案:购买根种跳绳,根种跳绳;
方案:购买根种跳绳,根种跳绳.
设购买跳绳所需总费用为元,则.
,
随的增大而减小,
当时,取得最小值,最小值.
答:在的条件下,购买方案需要的总费用最少,最少费用是元.
【解析】设购进一根种跳绳需元,购进一根种跳绳需元,根据“购进根种跳绳和根种跳绳共需元:购进根种跳绳和根种跳绳共需元”,即可得出关于,的二元一次方程组,解之即可得出结论;
设购买种跳绳根,则购买种跳绳根,利用总价单价数量,结合总价不少于元且不多于元,即可得出关于的一元一次不等式组,解之即可得出的取值范围,再结合为整数,即可得出各购买方案;
设购买跳绳所需总费用为元,利用总价单价数量,即可得出关于的函数关系式,再利用一次函数的性质,即可解决最值问题.
本题考查了二元一次方程组的应用、一元一次不等式组的应用以及一次函数的应用,解题的关键是:找准等量关系,正确列出二元一次方程组;根据各数量之间的关系,正确列出一元一次不等式组;根据各数量之间的关系,找出关于的函数关系式.
第1页,共1页
一、选择题(本大题共16小题,共42.0分。在每小题列出的选项中,选出符合题目的一项)
1. 如图所示,已知,下列结论正确的是( )
A.
B.
C.
D.
2. 下列命题:过一点有且只有一条直线与已知直线平行;过一点有且只有一条直线与已知直线垂直;同旁内角互补;垂直于同一条直线的两条直线垂直其中的假命题有( )
A. 个 B. 个 C. 个 D. 个
3. 若一个数的平方根是,则这个数的立方根是( )
A. B. C. D.
4. 在下列各数,,,,,两个之间,依次增加个,其中无理数有( )
A. 个 B. 个 C. 个 D. 个
5. 若点在第三象限,则点一定在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
6. 下列说法中,正确的是( )
的立方根是;
的算术平方根是;
的立方根是;
的平方根是.
A. 个 B. 个 C. 个 D. 个
7. 已知方程,用含的代数式表示( )
A. B. C. D.
8. 已知,则下列结论不成立的是( )
A. B. C. D.
9. 估计的值应在( )
A. 和之间 B. 和之间 C. 和之间 D. 和之间
10. 在平面直角坐标系中,已知线段的两个端点的坐标分别是、,将线段向上移动个单位,向左移动个单位平移后,点,的对应坐标为( )
A. , B. ,
C. , D. ,
11. 下列调查中,适合用全面调查的是( )
A. 调查某批次汽车的抗撞击能力
B. 调查春节联欢晚会的收视率
C. “神七”飞船发射前对重要零部件的检查
D. 调查市场上某种食品的色素含量是否符合国家标准
12. 如果关于的不等式的解集为,那么的取值范围是( )
A. B. C. D.
13. 下列说法正确的是( )
A. 点在第四象限
B. 若,则在坐标原点
C. 点在第二象限,且点到轴的距离为,点到轴的距离为,则点的坐标为
D. 在平面直角坐标系中,若点的坐标为,且平行于轴,,则点的坐标为
14. 把一堆练习本分给学生,如果每名学生分本,那么多本;如果每名学生分本,那么最后名学生只有本设有名学生,本书,根据题意,可列方程组为( )
A. B.
C. D.
15. 某次知识竞赛共有道题,答对一题得分,答错或不答均扣分,小玉得分超过分,他至少要答对道题.( )
A. B. C. D.
16. 关于,的方程组的解中与的和不小于,则的取值范围为( )
A. B. C. D.
二、填空题(本大题共5小题,共11.0分)
17. 的平方根是______ .
18. 若点在第二象限,则的取值范围是______ .
19. 如图,在长方形中,,,,则点的坐标为______ .
20. 安排学生住宿,若每间住人,则还有人无房可住;若每间住人,则还有一间不空也不满,则宿舍的房间数量可能为______ .
21. 如图,岛在岛的北偏东方向,岛在岛的北偏西方向,则的大小是______.
三、解答题(本大题共7小题,共67.0分。解答应写出文字说明,证明过程或演算步骤)
22. 本小题分
图形的世界丰富且充满变化,用数学的眼光观察它们,奇妙无比.
如图,,数学课上,老师请同学们根据图形特征添加一个关于角的条件,使得,并给出证明过程.
小丽添加的条件:.
请你帮小丽将下面的证明过程补充完整.
证明:已知
____________
已知
____________
____________
等量代换
拓展:如图,请你从三个选项,平分,中任选出两个作为条件,另一个作为结论,组成一个真命题,并加以证明.
条件:______,结论:______填序号.
证明:______.
23. 本小题分
解方程组;
解不等式组并在数轴上表示解集.
24. 本小题分
已知点,请分别根据下列条件,求出点的坐标.
点在轴上,则点坐标为______;
点的横坐标比纵坐标大;
点在过点且与轴平行的直线上.
25. 本小题分
已知正数的两个不等的平方根分别是和,的立方根为;是的整数部分;求的平方根.
26. 本小题分
某校举行全体学生“汉字听写”比赛,每位学生听写汉字个.现随机抽取了部分学生的听写结果,绘制成如下的图表:
组别 正确字数 人数
根据以上信息完成下列问题:
统计表中的______,______,并补全条形统计图.
扇形统计图中“组”所对应的圆心角的度数是______.
已知该校共有名学生,如果听写正确的字的个数少于个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
27. 本小题分
如图,三角形中任意一点经平移后对应点为,,,,将三角形作同样的平移得到三角形.
写出坐标:______ ,______ ,______ ,______ ,______ ,______ ,并画出三角形;
三角形的面积为______ ;
已知点在轴上,且三角形的面积等于三角形的面积,求点坐标.
28. 本小题分
学校开展大课间活动,某班需要购买、两种跳绳.已知购进根种跳绳和根种跳绳共需元:购进根种跳绳和根种跳绳共需元.
求购进一根种跳绳和一根种跳绳各需多少元?
设购买种跳绳根,若班级计划购买、两种跳绳共根,所花费用不少于元且不多于元,则有哪几种购买方案?
在的条件下,哪种购买方案需要的总费用最少?最少费用是多少元?
答案和解析
1.【答案】
【解析】解:,
,
故选:.
根据平行线的性质即可得到结论.
本题考查了平行线的性质,熟练掌握两直线平行,同位角相等是解题的关键.
2.【答案】
【解析】解:过直线外一点有且只有一条直线与已知直线平行,故原命题错误,是假命题;
过直线外一点有且只有一条直线与已知直线垂直,故原命题错误,是假命题;
两直线平行,同旁内角互补,故原命题错误,是假命题;
平面内垂直于同一条直线的两条直线平行,故原命题错误,是假命题.
假命题有个,
故选:.
利用平行公理及有关平面内两直线的位置关系分别判断后即可确定正确的选项.
本题考查了命题与定理的知识,解题的关键是了解平行线的性质及平行公理等知识,难度不大.
3.【答案】
【解析】解:一个数的平方根是,
这个数为,
故的立方根是.
故选:.
首先利用平方根的定义求出这个数,然后根据立方根的定义即可求解.
此题主要考查了立方根的定义,求一个数的立方根,应先找出所要求的这个数是哪一个数的立方.由开立方和立方是互逆运算,用立方的方法求这个数的立方根.注意一个数的立方根与原数的性质符号相同.
4.【答案】
【解析】解:,
,,是有理数,
,,两个之间,依次增加个是无理数,
无理数有个,
故选:.
根据无理数、有理数的定义解答即可.
此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如,,每两个之间依次多个等形式.
5.【答案】
【解析】解:点在第三象限,
,,
,,
点一定在第二象限.
故选:.
根据第三象限的点的坐标特征求出、的正负情况,然后判断出点所在的象限即可.
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解题的关键,四个象限的符号特点分别是:第一象限,第二象限,第三象限,第四象限.
6.【答案】
【解析】解:的立方根是,原说法正确;
的算术平方根是,原说法错误;
的立方根是,原说法正确;
的平方根是,原说法错误;
正确的个数有个;
故选:.
根据立方根、平方根和算术平方根的定义分别对每小题进行分析,即可得出答案.
此题考查了立方根、平方根和算术平方根,熟练掌握立方根、平方根和算术平方根的定义是解题的关键.
7.【答案】
【解析】解:,
移项、得.
故选:.
把含的项放到方程左边,移项即可.
本题考查的是方程的基本运算技能:移项、合并同类项、系数化为等,表示谁就该把谁放到等号的一边,其他的项移到另一边,然后合并同类项、系数化就可用含的式子表示的形式.
8.【答案】
【解析】解:、由,可得,成立;
B、由,可得,不成立;
C、由,可得,成立;
D、由,可得,成立;
故选:.
根据不等式的性质解答即可.
此题考查不等式的性质,关键是根据不等式的性质解答.
9.【答案】
【解析】解:,
,
故选:.
直接利用平方数可知,从而估算无理数的大小.
此题主要考查了估算无理数的大小,正确估算无理数是解题关键.
10.【答案】
【解析】解:线段向上移动个单位,向左移动个单位平移,
平移后、对应坐标为、,
即,.
故选:.
根据将线段向上移动个单位,向左移动个单位平移,纵坐标加,横坐标减,从而得出答案.
本题考查图形的平移变换,关键是要懂得左右平移点的纵坐标不变,而上下平移时点的横坐标不变,平移变换是中考的常考点.比较对应点的坐标变化,寻找变化规律,并把变化规律运用到其它对应点上.
11.【答案】
【解析】解:、调查某批次汽车的抗撞击能力,具有破坏性,适合采用抽样调查,故本选项不合题意;
B、调查春节联欢晚会的收视率,范围广,人数多,适合采用抽样调查,故本选项不符合题意;
C、“神七”飞船发射前对重要零部件的检查,涉及安全性,适合采用全面调查,故本选项符合题意;
D、调查市场上某种食品的色素含量是否符合国家标准,范围广,适合采用抽样调查,故本选项不合题意.
故选:.
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
12.【答案】
【解析】解:不等式的解集为,
,
故选:.
运用不等式的基本性质求解即可.
本题考查了不等式的基本性质,解题的关键是熟记不等式的基本性质.
13.【答案】
【解析】
【分析】
本题主要考查了坐标与图形性质,熟练掌握坐标与图形性质进行求解是解决本题的关键.
应用坐标与图形性质进行判定即可得出答案.
【解答】
解:因为当时,点在轴上,所以选项说法不一定正确,故A选项不符合题意;
B.因为当,,或,时,,则在轴或轴上,不一定在坐标原点,所以选项说法不一定正确,故B选项不符合题意;
C.因为点在第二象限,且点到轴的距离为,点到轴的距离为,则点的坐标为,所以选项说法正确,故C选项符合题意;
D.因为在平面直角坐标系中,若点的坐标为,且平行于轴,,则点的坐标为或,所以选项说法正确,故D选项不符合题意.
故选:.
14.【答案】
【解析】解:依题意,得:.
故选:.
根据“如果每名学生分本,那么多本;如果每名学生分本,那么最后名学生只有本”,即可得出关于,的二元一次方程组,此题得解.
本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
15.【答案】
【解析】解:设小玉答对了道题,
解得,
小玉至少答对道,
故选:.
根据题意可以列出相应的不等式,从而可以求得的取值范围,由于是整数,从而可以解答本题.
本题考查一元一次不等式的应用,解题的关键是明确题意,列出相应的一元一次不等式.
16.【答案】
【解析】解:把两个方程相减,可得,
根据题意得:,
解得:.
所以的取值范围是.
故选:.
两个方程相减可得出,根据列出关于的不等式,解之可得答案.
本题主要考查解一元一次不等式,解二元一次方程组,解题的关键是掌握解一元一次不等式的能力、不等式的基本性质等知识点.
17.【答案】
【解析】解:,
的平方根是.
故答案为:.
如果一个数的平方等于,这个数就叫做的平方根,如果一个正数的平方等于,即,那么这个正数叫做的算术平方根.记为,由此即可得到答案.
本题考查平方根、算术平方根,关键是掌握平方根、算术平方根的定义.
18.【答案】
【解析】解:由题意可得:,
解得:.
故答案为:.
根据第二象限的点的特征,列出不等式组,解之即可.
本题考查了解一元一次不等式组,掌握各象限点的坐标特征是解题关键.
19.【答案】
【解析】解:,,
,轴,
四边形是长方形,
,轴,
同理可得轴,
点,
点的坐标为,
故答案为:.
先根据、的坐标求出的长,则,并证明轴,同理可得轴,由此即可得到答案.
本题主要考查了坐标与图形,熟知长方形的性质是解题的关键.
20.【答案】或或或
【解析】解:设共有间宿舍,则共有个学生,
依题意得:,
解得:.
又为正整数,
或或或.
故答案为:或或或.
设共有间宿舍,则共有个学生,然后根据每间住人,则还有一间不空也不满,列出不等式组进行求解即可.
本题主要考查了一元一次不等式组的应用,解题的关键在于能够准确根据题意列出不等式组进行求解.
21.【答案】
【解析】解:过点作,如图,
,
,
,,
,
由岛在岛的北偏东方向,岛在岛的北偏西方向,得
,.
,
故答案为:.
过点作,根据平行线的性质,求得与,再由角的和差可得答案.
本题考查了方向角,平行线的性质,利用平行线的性质得出得出,是解题关键.
22.【答案】;两直线平行,同位角相等;;同旁内角互补,两直线平行;;两直线平行,内错角相等;
;;答案不唯一
,
,,
,
,即平分.
【解析】证明:已知,
两直线平行,同位角相等,
已知,
同旁内角互补,两直线平行,
两直线平行,内错角相等,
等量代换;
故答案为;两直线平行,同位角相等;;同旁内角互补,两直线平行;;两直线平行,内错角相等;
条件:,,
结论:平分,
证明:,
,,
,
,即平分.
故答案为;;答案不唯一
,
,,
,
,即平分.
根据平行线的判定定理和性质定理解答;
根据真命题的概念写出命题的条件和结论,根据平行线的判定定理和性质定理、角平分线的定义解答.
本题考查的是命题的真假判断、平行线的判定和性质,掌握平行线的判定定理和性质定理是解题的关键.
23.【答案】解:,
得:,
解得,
把代入得:,
解得,
方程组的解为;
,
解不等式得:,
解不等式得:,
不等式组无解,
数轴表示如下:
【解析】利用加减消元法解二元一次方程组即可;
按照解一元一次不等式组的步骤,先求出两个不等式的解集,然后再求出不等式组的解集,最后在数轴上表示出不等式组的解集即可.
本题主要考查了解二元一次方程组,解一元一次不等式组,熟知相关计算方法是解题的关键.
24.【答案】解:;
点的横坐标比纵坐标大,
,
,
,,
点坐标为;
点在过点且与轴平行的直线上,
点的横坐标为,
,
,
,
点坐标为.
【解析】解:点在轴上,
,
,
,
点坐标为,
故答案为:;
点的横坐标比纵坐标大,
,
,
,,
点坐标为;
点在过点且与轴平行的直线上,
点的横坐标为,
,
,
,
点坐标为.
直接利用轴上点的坐标特点求出的值,即可求出点的坐标;
利用点的横坐标比纵坐标大求出的值,即可求出点的坐标;
利用点在过点且与轴平行的直线上,横坐标相同出的值,即可求出点的坐标.
本题考查了坐标与图形的性质,正确分析各点的坐标特点是解决问题的关键.
25.【答案】解:正数的两个不等的平方根分别是和,
,
解得:,
的立方根为,
,
解得:,
是的整数部分,
,
,
的平方根是.
【解析】根据平方根定义、立方根定义和无理数的估算求出、、的值,然后再求出的值即可得出答案.
本题主要考查了平方根、立方根和无理数的估算,解题的关键是求出,,.
26.【答案】解:;;
补全条形统计图如下:
;
估计这所学校本次听写比赛不合格的
学生人数为:
人.
【解析】
【分析】
本题考查的是频数分布表、条形图和扇形图的知识,利用统计图获取正确信息是解题的关键.注意频数、频率和样本容量之间的关系的应用.
根据条形图和扇形图确定组的人数所占的百分比求出样本容量,求出、的值;
求出组”所占的百分比,得到所对应的圆心角的度数;
求出不合格人数所占的百分比,求出该校本次听写比赛不合格的学生人数.
【解答】
解:从条形图可知,组有人,
从扇形图可知,组所占的百分比是,组所占的百分比是,组所占的百分比是,
,
,
,
,;
补全条形统计图如图;
故答案为;
“组”所对应的圆心角的度数是;
故答案为;
见答案.
27.【答案】
【解析】解:,,;如图,为所作;
三角形的面积;
故答案为,;,;,;;
设,
三角形的面积等于三角形的面积,
,解得,,
点坐标为或
利用点和的坐标特征确定平移的规律,然后写出、、的坐标,再描点即可;
用一个矩形的面积分别减去三个直角三角形的面积去计算三角形的面积;
设,利用三角形面积公式得,然后解方程求出,从而得到点坐标.
本题考查了作图平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
28.【答案】解:设购进一根种跳绳需元,购进一根种跳绳需元,
依题意得:,
解得:.
答:购进一根种跳绳需元,购进一根种跳绳需元.
该班级计划购买、两种跳绳共根,且购买种跳绳根,
购买种跳绳根.
依题意得:,
解得:,
又为整数,
可以取,,,
共有种购买方案,
方案:购买根种跳绳,根种跳绳;
方案:购买根种跳绳,根种跳绳;
方案:购买根种跳绳,根种跳绳.
设购买跳绳所需总费用为元,则.
,
随的增大而减小,
当时,取得最小值,最小值.
答:在的条件下,购买方案需要的总费用最少,最少费用是元.
【解析】设购进一根种跳绳需元,购进一根种跳绳需元,根据“购进根种跳绳和根种跳绳共需元:购进根种跳绳和根种跳绳共需元”,即可得出关于,的二元一次方程组,解之即可得出结论;
设购买种跳绳根,则购买种跳绳根,利用总价单价数量,结合总价不少于元且不多于元,即可得出关于的一元一次不等式组,解之即可得出的取值范围,再结合为整数,即可得出各购买方案;
设购买跳绳所需总费用为元,利用总价单价数量,即可得出关于的函数关系式,再利用一次函数的性质,即可解决最值问题.
本题考查了二元一次方程组的应用、一元一次不等式组的应用以及一次函数的应用,解题的关键是:找准等量关系,正确列出二元一次方程组;根据各数量之间的关系,正确列出一元一次不等式组;根据各数量之间的关系,找出关于的函数关系式.
第1页,共1页
同课章节目录
