有 理 数 的 乘法[下学期]
文档属性
| 名称 | 有 理 数 的 乘法[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 66.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-07-19 00:00:00 | ||
图片预览






文档简介
课件15张PPT。安吉县实验初中 杨晶晶 金旭东2.9有理数的乘法 第一课时
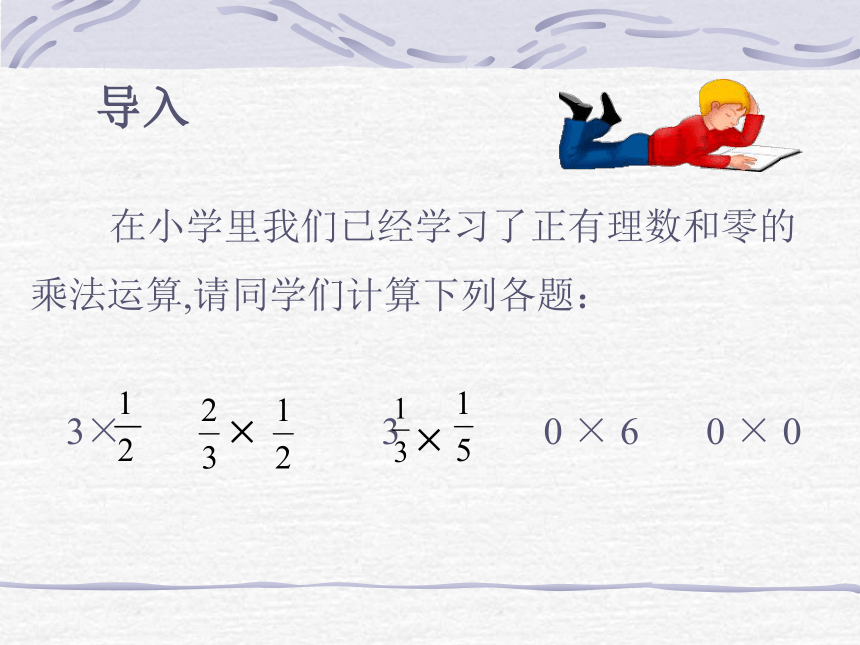
有理数的乘法法则 导入 在小学里我们已经学习了正有理数和零的
乘法运算,请同学们计算下列各题: 3× 3 0 × 6 0 × 0问题: 一只小鱼沿一条东西向的路线,以每分钟3米的速度向某方向游了2分钟,那么它现在位于原来位置的哪个方向?相距多少米? 演示动画演示 我们必须把问题说得明确些,并规定向东为正, 向西为负.
(1)若小鱼向东游,我们可用乘法表示: 3×2 = 6 即小鱼位于原来位置的东方6米处.
(宏控制的动画需在office 2000中运行)(2)若小鱼向西游,我们也可以用乘法表示:(-3)× 2 = - 6 即小鱼位于原来位置的西方6米处.
(3)若速度改为每分钟4米,请同学们写出算式.
(宏控制的动画需在office 2000中运行)寻找规律
(1)想一想
3×2 = 6 (-3)× 2 = - 6
4×2 = 6 (-4)×2 = - 6
比较上面四个算式,有什么发现?(因数、积的符号、绝对值等)
规律:
把一个因数换成它的相反数,所得的积是原来积的相反数.
- 6 60 如何确定两个有理数的积的符号和绝对值?从以上得出的几个算式,你能发现什么规律?
探索总结
有理数的乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与零相乘,都得零.
例如:
(-5)×(-3) (-5)×(-3)= +() 5×3=15 所以(-5)×(-3)=15.
----------------------同号两数相乘 --------------------------得正
-----------------------------把绝对值相乘 再如: (-6)×4 (-6)×4= -() 6×4=24 所以(-6)×4= -24. -----------------------异号两数相乘 --------------------------------------得负 ------------------------------把绝对值相乘 展开应用
1、例题
(1)(-5)×(-6) (2)(- )×4 (3) (-1 )× 2、(口答)确定下列两数的积的符号:
(1) 5×(-3) (2) (-3)×3
(3) (-2)×(-7) (4) ×
3、完成课本52页练习24、计算并找规律:
(1) 3×(-1); (2) (-5)×(-1);
(3) ×(-1); (4) 0×(-1);
(5) (-6)×1; (6) 2×1;
(7) 0×1; (8) 1×(-1)
做完这题,你能发现什么规律?一个数与1相乘,积是什么?一个数与(-1)相乘呢?(1)若ab﹥0,则必有 ( )
A、a﹥0 ,b﹥0 B 、a﹤0 ,b﹤0
C 、a﹥0 ,b﹤0 D 、a,b 同号
(2)若ab=0则一定有 ( )
A、 a=b=0 B 、a=0
C 、 a,b 至少有一个为 0 D、a,b 最多有一个为 05、精心想一想
课堂小结 1、本节课学会了那些知识和方法?试谈谈你
的感受. 2、你知道有理数的乘法与小学算术数的乘法
有何异同吗?在运用有理数的乘法法则时
应注意什么问题?
再见!
有理数的乘法法则 导入 在小学里我们已经学习了正有理数和零的
乘法运算,请同学们计算下列各题: 3× 3 0 × 6 0 × 0问题: 一只小鱼沿一条东西向的路线,以每分钟3米的速度向某方向游了2分钟,那么它现在位于原来位置的哪个方向?相距多少米? 演示动画演示 我们必须把问题说得明确些,并规定向东为正, 向西为负.
(1)若小鱼向东游,我们可用乘法表示: 3×2 = 6 即小鱼位于原来位置的东方6米处.
(宏控制的动画需在office 2000中运行)(2)若小鱼向西游,我们也可以用乘法表示:(-3)× 2 = - 6 即小鱼位于原来位置的西方6米处.
(3)若速度改为每分钟4米,请同学们写出算式.
(宏控制的动画需在office 2000中运行)寻找规律
(1)想一想
3×2 = 6 (-3)× 2 = - 6
4×2 = 6 (-4)×2 = - 6
比较上面四个算式,有什么发现?(因数、积的符号、绝对值等)
规律:
把一个因数换成它的相反数,所得的积是原来积的相反数.
- 6 60 如何确定两个有理数的积的符号和绝对值?从以上得出的几个算式,你能发现什么规律?
探索总结
有理数的乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与零相乘,都得零.
例如:
(-5)×(-3) (-5)×(-3)= +() 5×3=15 所以(-5)×(-3)=15.
----------------------同号两数相乘 --------------------------得正
-----------------------------把绝对值相乘 再如: (-6)×4 (-6)×4= -() 6×4=24 所以(-6)×4= -24. -----------------------异号两数相乘 --------------------------------------得负 ------------------------------把绝对值相乘 展开应用
1、例题
(1)(-5)×(-6) (2)(- )×4 (3) (-1 )× 2、(口答)确定下列两数的积的符号:
(1) 5×(-3) (2) (-3)×3
(3) (-2)×(-7) (4) ×
3、完成课本52页练习24、计算并找规律:
(1) 3×(-1); (2) (-5)×(-1);
(3) ×(-1); (4) 0×(-1);
(5) (-6)×1; (6) 2×1;
(7) 0×1; (8) 1×(-1)
做完这题,你能发现什么规律?一个数与1相乘,积是什么?一个数与(-1)相乘呢?(1)若ab﹥0,则必有 ( )
A、a﹥0 ,b﹥0 B 、a﹤0 ,b﹤0
C 、a﹥0 ,b﹤0 D 、a,b 同号
(2)若ab=0则一定有 ( )
A、 a=b=0 B 、a=0
C 、 a,b 至少有一个为 0 D、a,b 最多有一个为 05、精心想一想
课堂小结 1、本节课学会了那些知识和方法?试谈谈你
的感受. 2、你知道有理数的乘法与小学算术数的乘法
有何异同吗?在运用有理数的乘法法则时
应注意什么问题?
再见!
