多边形的内角和[下学期]
文档属性
| 名称 | 多边形的内角和[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 398.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-14 00:00:00 | ||
图片预览




文档简介
课件14张PPT。7.3.2 多边形的内角和三角形的内角和等于 .正方形、长
方形的内角和都等于 .?思考其他四边形的内角和等于多少?任意画一个四边形,量出它的4个内角,计算它们的和。再与其他同学比较一下,你能得出什么结论?能否利用三角形内角和等于180°得出这个结论?从四边形的一个顶点出发,可以引 1 条对角线,它将四边形分为 2 个三角形,四边形的内角和等于180°×2
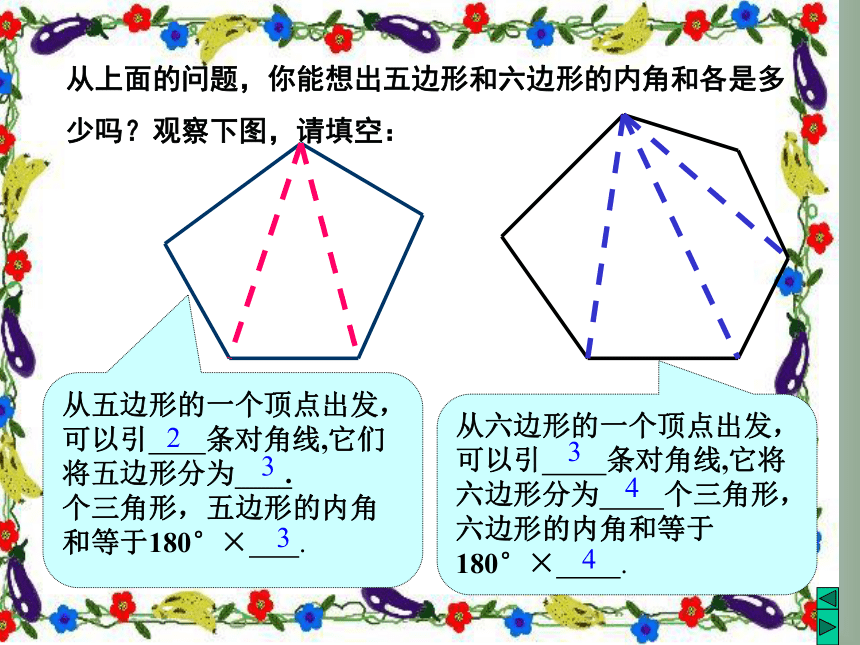
从上面的问题,你能想出五边形和六边形的内角和各是多
少吗?观察下图,请填空:从五边形的一个顶点出发,可以引 条对角线,它们将五边形分为 . 个三角形,五边形的内角和等于180°× .
从六边形的一个顶点出发,可以引 条对角线,它将六边形分为 个三角形,六边形的内角和等于180°× .
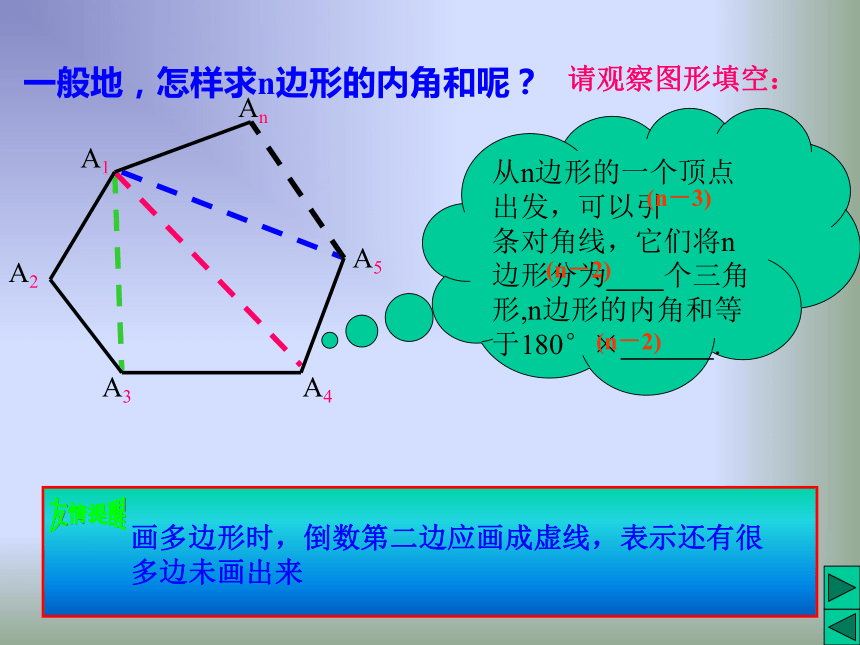
一般地,怎样求n边形的内角和呢?请观察图形填空:从n边形的一个顶点出发,可以引 条对角线,它们将n边形分为 个三角形,n边形的内角和等于180°× .
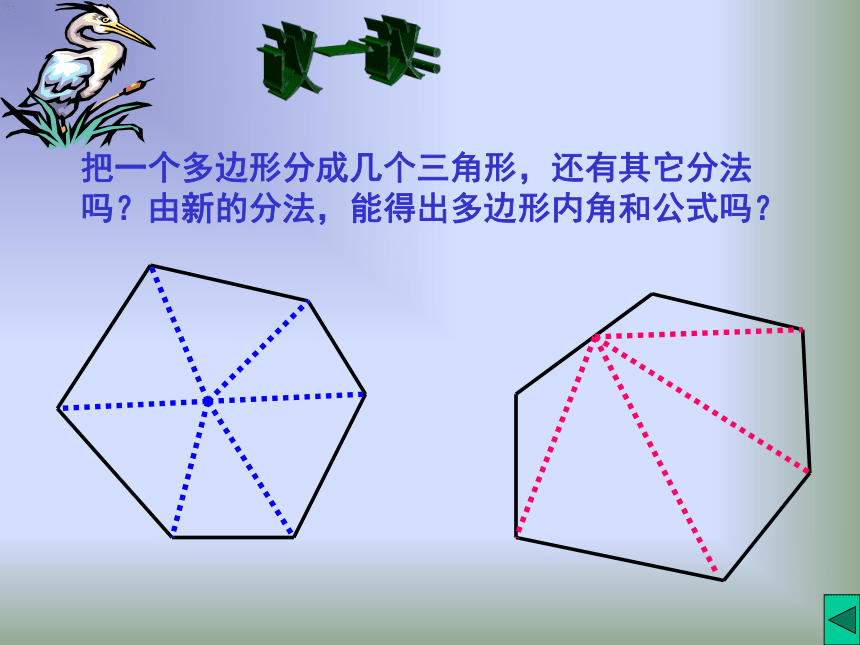
议一议:把一个多边形分成几个三角形,还有其它分法吗?由新的分法,能得出多边形内角和公式吗?根据以上的探讨,就得出
了多边形的内角和公式:n边形的内角和等于(n-2)·180°基础训练十二边形的内角和为 °
一个多边形的内角和为1080°则这个多边形的边数为 .
一个四边形的四个内角之比为7:8:2:1,则这四个角的大小分别为 °、 °、
°、 °
81800能力训练如果一个四边形的一组对角互补,那么另一组对角有什么关系?解: 如右图,四边形ABCD中,
∠A+∠C=180°.∵ ∠A+∠B+∠C+∠D=(4-2) ×180°=360 °∴ ∠B+∠D=360°-(∠A+∠C) =360°-180°=180°这就是说,如果四边形的一组对角互补,那么另一组对角也互补.已知一个多边形各个内角都相等,都等
于150°,求这个多边形的边数.解:设此多边形的边数为n,根据题意,得(n-2)· 180°=n · 150解得 n = 12则这个多边形的边数为12条探索与创新
本节课你收获了什么?小结:再见
方形的内角和都等于 .?思考其他四边形的内角和等于多少?任意画一个四边形,量出它的4个内角,计算它们的和。再与其他同学比较一下,你能得出什么结论?能否利用三角形内角和等于180°得出这个结论?从四边形的一个顶点出发,可以引 1 条对角线,它将四边形分为 2 个三角形,四边形的内角和等于180°×2
从上面的问题,你能想出五边形和六边形的内角和各是多
少吗?观察下图,请填空:从五边形的一个顶点出发,可以引 条对角线,它们将五边形分为 . 个三角形,五边形的内角和等于180°× .
从六边形的一个顶点出发,可以引 条对角线,它将六边形分为 个三角形,六边形的内角和等于180°× .
一般地,怎样求n边形的内角和呢?请观察图形填空:从n边形的一个顶点出发,可以引 条对角线,它们将n边形分为 个三角形,n边形的内角和等于180°× .
议一议:把一个多边形分成几个三角形,还有其它分法吗?由新的分法,能得出多边形内角和公式吗?根据以上的探讨,就得出
了多边形的内角和公式:n边形的内角和等于(n-2)·180°基础训练十二边形的内角和为 °
一个多边形的内角和为1080°则这个多边形的边数为 .
一个四边形的四个内角之比为7:8:2:1,则这四个角的大小分别为 °、 °、
°、 °
81800能力训练如果一个四边形的一组对角互补,那么另一组对角有什么关系?解: 如右图,四边形ABCD中,
∠A+∠C=180°.∵ ∠A+∠B+∠C+∠D=(4-2) ×180°=360 °∴ ∠B+∠D=360°-(∠A+∠C) =360°-180°=180°这就是说,如果四边形的一组对角互补,那么另一组对角也互补.已知一个多边形各个内角都相等,都等
于150°,求这个多边形的边数.解:设此多边形的边数为n,根据题意,得(n-2)· 180°=n · 150解得 n = 12则这个多边形的边数为12条探索与创新
本节课你收获了什么?小结:再见
