多边形的内角和与外角和[下学期]
文档属性
| 名称 | 多边形的内角和与外角和[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 85.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-27 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
9.2 多边形的内角和与外角和
第一课时
知识回顾
1 什么是三角形?
2 三角形的内角和是多少度?
三角形的外角和是多少度?
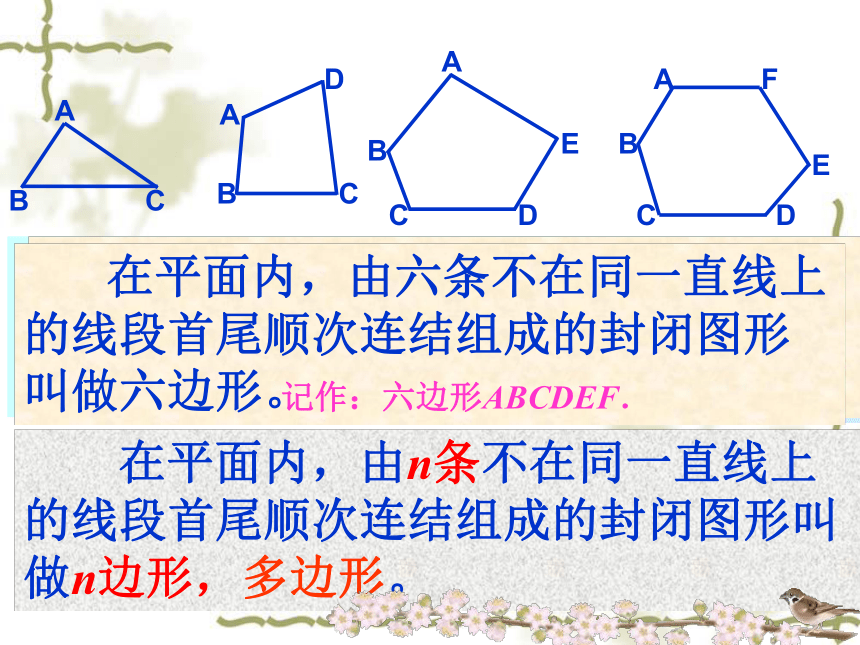
在平面内,由三条不在同一直线上的线段首尾顺次连结组成封闭图形叫做三角形。
在平面内,由n条不在同一直线上的线段首尾顺次连结组成的封闭图形叫做n边形,多边形。
A
B
C
A
B
C
D
A
B
C
D
E
A
B
C
E
D
F
记作:△ABC.
在平面内,由四条不在同一直线上的线段首尾顺次连结组成的封闭图形叫做四边形。
记作:四边形ABCD.
在平面内,由五条不在同一直线上的线段首尾顺次连结组成的封闭图形叫做五边形。
记作:五边形ABCDE.
在平面内,由六条不在同一直线上的线段首尾顺次连结组成的封闭图形叫做六边形。
记作:六边形ABCDEF.
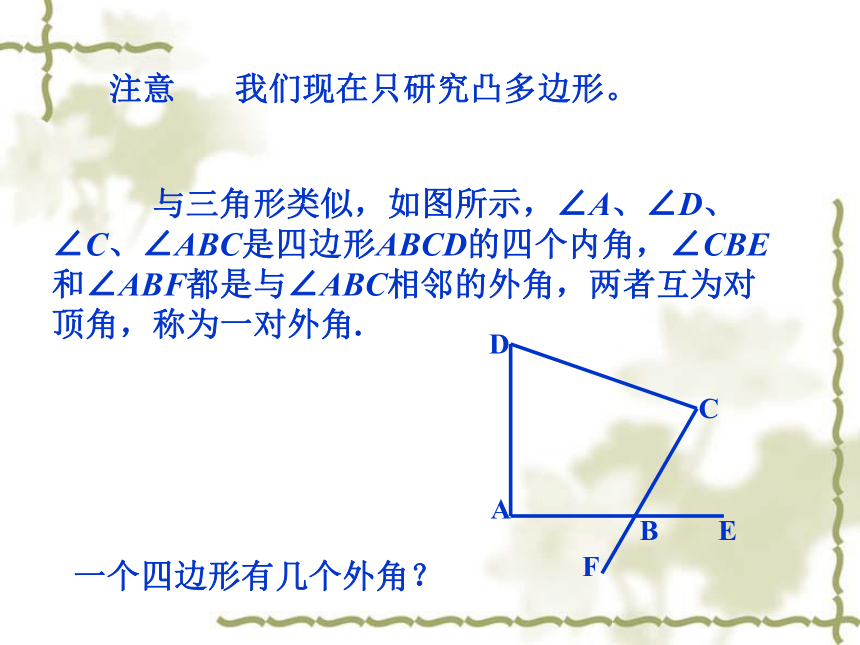
与三角形类似,如图所示,∠A、∠D、∠C、∠ABC是四边形ABCD的四个内角,∠CBE和∠ABF都是与∠ABC相邻的外角,两者互为对顶角,称为一对外角.
C
A
B
D
F
E
注意 我们现在只研究凸多边形。
一个四边形有几个外角?
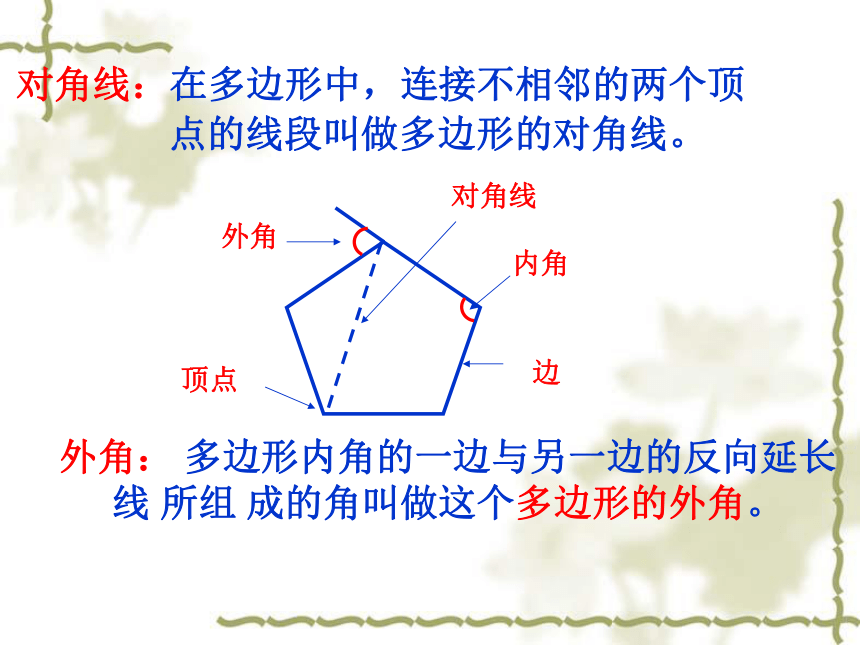
顶点
内角
边
外角
对角线
对角线:在多边形中,连接不相邻的两个顶
点的线段叫做多边形的对角线。
外角: 多边形内角的一边与另一边的反向延长 线 所组 成的角叫做这个多边形的外角。
问题 1 五边形、六边形分别有多少个内角?多少个外角?
答 五边形有5个内角,10个(5对)外角;
六边形有6个内角,12个(6对)外角.
问题 n边形有多少个内角?多少个外角?
答 n边形有n个内角,2n个(n对)外角.
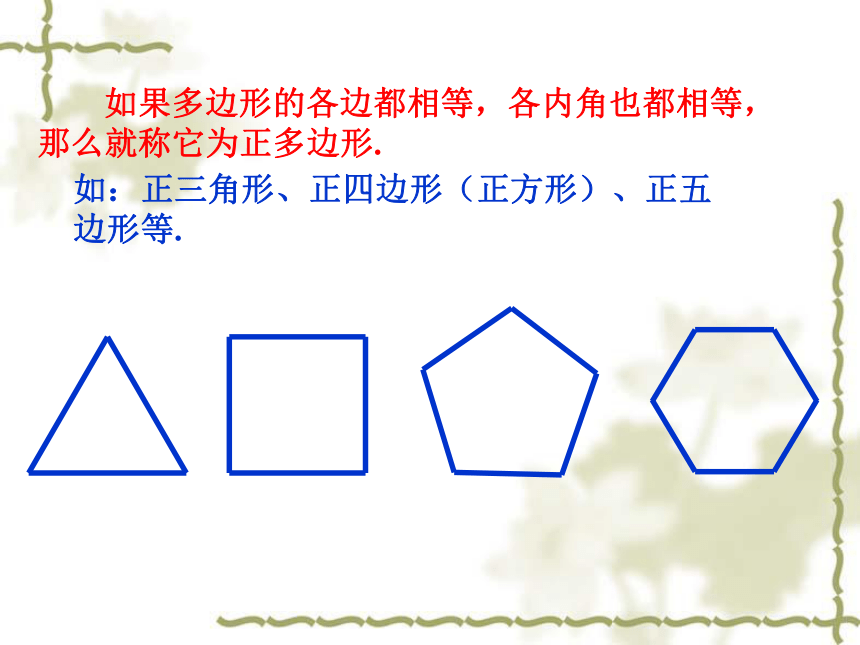
如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
如:正三角形、正四边形(正方形)、正五边形等.
议一议:
(1)一个多边形的边都相等,它的内角一定都相等吗?
(2)一个多边形的内角都相等,它的边一定都相等吗?
A
B
D
E
C
C
A
B
D
A
B
D
E
C
F
如图可以看出,从多边形的一个顶点引出的对角线把多边形划分为若干个三角形,我们已知一个三角形的内角和等于180°,那么四边形的内角和等于多少度?五边形、六边形呢?由此,n边形的内角和等于多少呢?
试一试
多边形的内角和
分成的三角形个数
n
…
6
5
4
3
多边形的边数
n-2
(n-2)·180°
1
2
3
4
180°
360°
540°
720°
…
…
结论 n边形的内角和为(n-2)·180°.
A
B
C
A
B
C
D
A
B
C
D
E
A
B
C
E
D
F
探索
例1 求八边形的内角和的度数.
练习 十边形的内角和是多少?若十边形的各个内角都相等,那么它的一个内角是多少度?
解 (n-2)·180°=(8-2)×180°=1080°.
例2 (1)一个多边形的内角和等于2340°,求它的边数;
(2)一个正多边形的一个内角为150°,你知道它是几边形?
解
(1)设边数为n,则有
(n-2)·180°=2340°
(2)设这个多边形为n边形,则有
n-2=13
(n-2)·180°=150°n
n=15;
n=12
这是个十二边形.
(1)一个多边形的内角和等于1260°,则这个多边形是 边形;
(2)一个多边形的每一个内角都是120°,则这个多边形是 边形.
练习
试一试
如图,在n边形内任取一点P与多边形的每一个顶点,可得几个三角形?(图中取n=6的情形)你能否根据这样划分多边形的方法来说明n边形的内角和等于(n-2)×180。?
●
1.先任意画一个五边形,然后画出它所有的对角线,数一数,一共有多少条对角线?
2.如果四边形有一个角是直角,另外三个角的度数之比为2∶3∶4,那么这三个内角的度数分别是多少?
3.一个多边形的内角和等于1080°,求它的边数.
4.一个多边形的每一个内角都等于144°,求它的边数.
作业
小结
本节课你的收获和体会是什么?
你有几种方法求得n边形的内角和?每种方法的关键做法是什么?
9.2 多边形的内角和与外角和
第一课时
知识回顾
1 什么是三角形?
2 三角形的内角和是多少度?
三角形的外角和是多少度?
在平面内,由三条不在同一直线上的线段首尾顺次连结组成封闭图形叫做三角形。
在平面内,由n条不在同一直线上的线段首尾顺次连结组成的封闭图形叫做n边形,多边形。
A
B
C
A
B
C
D
A
B
C
D
E
A
B
C
E
D
F
记作:△ABC.
在平面内,由四条不在同一直线上的线段首尾顺次连结组成的封闭图形叫做四边形。
记作:四边形ABCD.
在平面内,由五条不在同一直线上的线段首尾顺次连结组成的封闭图形叫做五边形。
记作:五边形ABCDE.
在平面内,由六条不在同一直线上的线段首尾顺次连结组成的封闭图形叫做六边形。
记作:六边形ABCDEF.
与三角形类似,如图所示,∠A、∠D、∠C、∠ABC是四边形ABCD的四个内角,∠CBE和∠ABF都是与∠ABC相邻的外角,两者互为对顶角,称为一对外角.
C
A
B
D
F
E
注意 我们现在只研究凸多边形。
一个四边形有几个外角?
顶点
内角
边
外角
对角线
对角线:在多边形中,连接不相邻的两个顶
点的线段叫做多边形的对角线。
外角: 多边形内角的一边与另一边的反向延长 线 所组 成的角叫做这个多边形的外角。
问题 1 五边形、六边形分别有多少个内角?多少个外角?
答 五边形有5个内角,10个(5对)外角;
六边形有6个内角,12个(6对)外角.
问题 n边形有多少个内角?多少个外角?
答 n边形有n个内角,2n个(n对)外角.
如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
如:正三角形、正四边形(正方形)、正五边形等.
议一议:
(1)一个多边形的边都相等,它的内角一定都相等吗?
(2)一个多边形的内角都相等,它的边一定都相等吗?
A
B
D
E
C
C
A
B
D
A
B
D
E
C
F
如图可以看出,从多边形的一个顶点引出的对角线把多边形划分为若干个三角形,我们已知一个三角形的内角和等于180°,那么四边形的内角和等于多少度?五边形、六边形呢?由此,n边形的内角和等于多少呢?
试一试
多边形的内角和
分成的三角形个数
n
…
6
5
4
3
多边形的边数
n-2
(n-2)·180°
1
2
3
4
180°
360°
540°
720°
…
…
结论 n边形的内角和为(n-2)·180°.
A
B
C
A
B
C
D
A
B
C
D
E
A
B
C
E
D
F
探索
例1 求八边形的内角和的度数.
练习 十边形的内角和是多少?若十边形的各个内角都相等,那么它的一个内角是多少度?
解 (n-2)·180°=(8-2)×180°=1080°.
例2 (1)一个多边形的内角和等于2340°,求它的边数;
(2)一个正多边形的一个内角为150°,你知道它是几边形?
解
(1)设边数为n,则有
(n-2)·180°=2340°
(2)设这个多边形为n边形,则有
n-2=13
(n-2)·180°=150°n
n=15;
n=12
这是个十二边形.
(1)一个多边形的内角和等于1260°,则这个多边形是 边形;
(2)一个多边形的每一个内角都是120°,则这个多边形是 边形.
练习
试一试
如图,在n边形内任取一点P与多边形的每一个顶点,可得几个三角形?(图中取n=6的情形)你能否根据这样划分多边形的方法来说明n边形的内角和等于(n-2)×180。?
●
1.先任意画一个五边形,然后画出它所有的对角线,数一数,一共有多少条对角线?
2.如果四边形有一个角是直角,另外三个角的度数之比为2∶3∶4,那么这三个内角的度数分别是多少?
3.一个多边形的内角和等于1080°,求它的边数.
4.一个多边形的每一个内角都等于144°,求它的边数.
作业
小结
本节课你的收获和体会是什么?
你有几种方法求得n边形的内角和?每种方法的关键做法是什么?
