5.2.2 直线平行的条件(1).[下学期]
文档属性
| 名称 | 5.2.2 直线平行的条件(1).[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 403.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-10 00:00:00 | ||
图片预览



文档简介
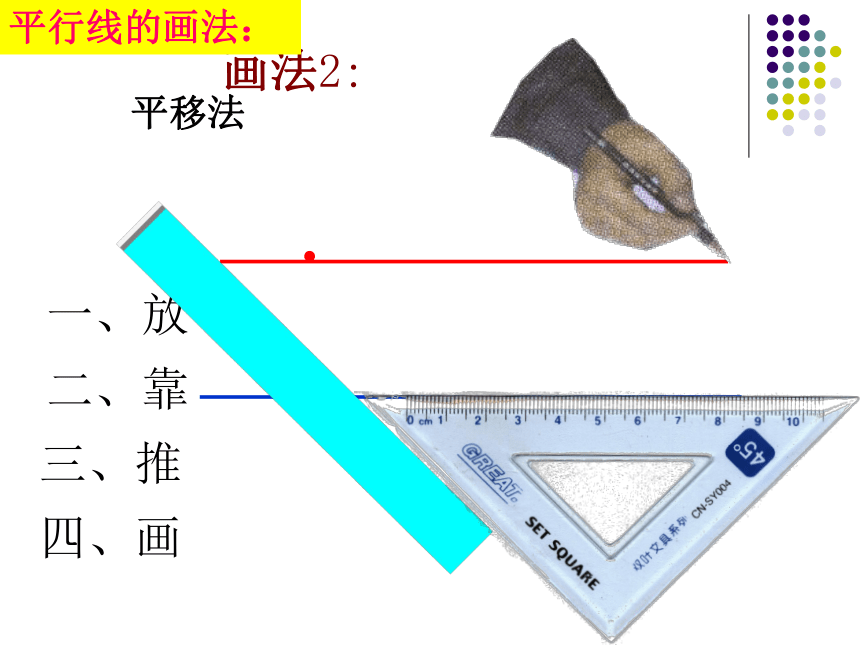
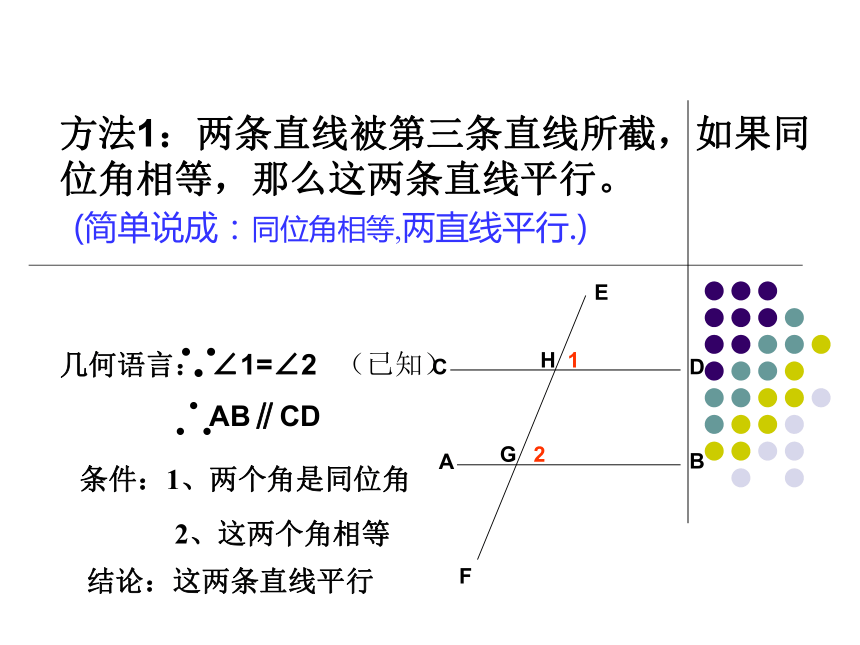
课件23张PPT。直线平行的条件(1)●一、放二、靠三、推四、画画法2:平行线的画法:平移法 方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。几何语言: ∠1=∠2
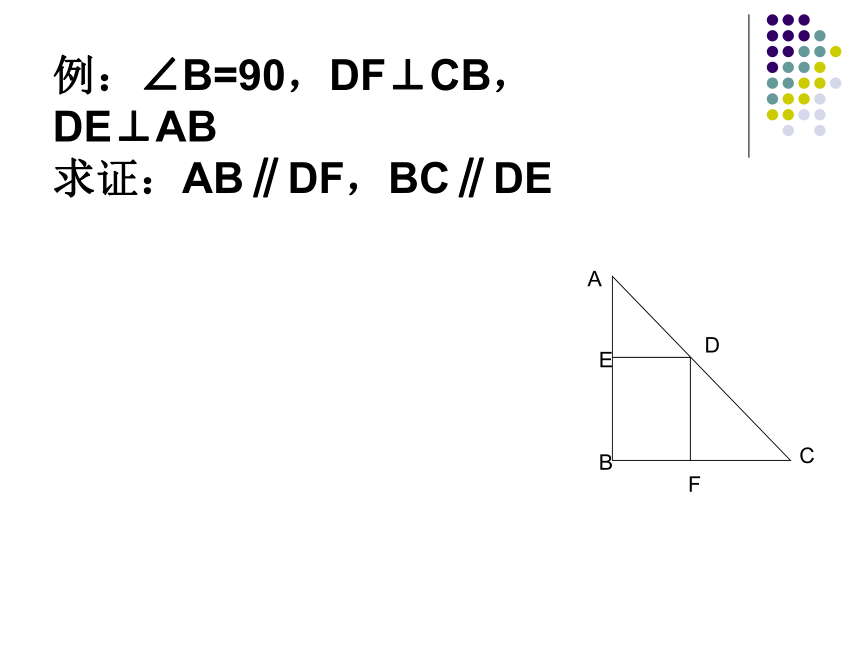
AB∥CD(简单说成:同位角相等,两直线平行.)结论:这两条直线平行条件:1、两个角是同位角2、这两个角相等(已知)例:∠B=90,DF⊥CB,DE⊥AB
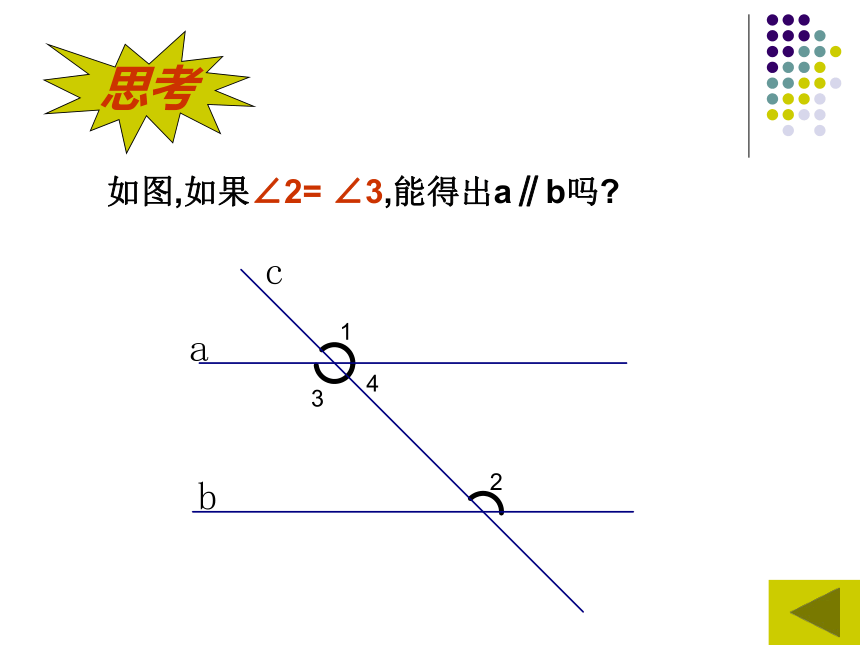
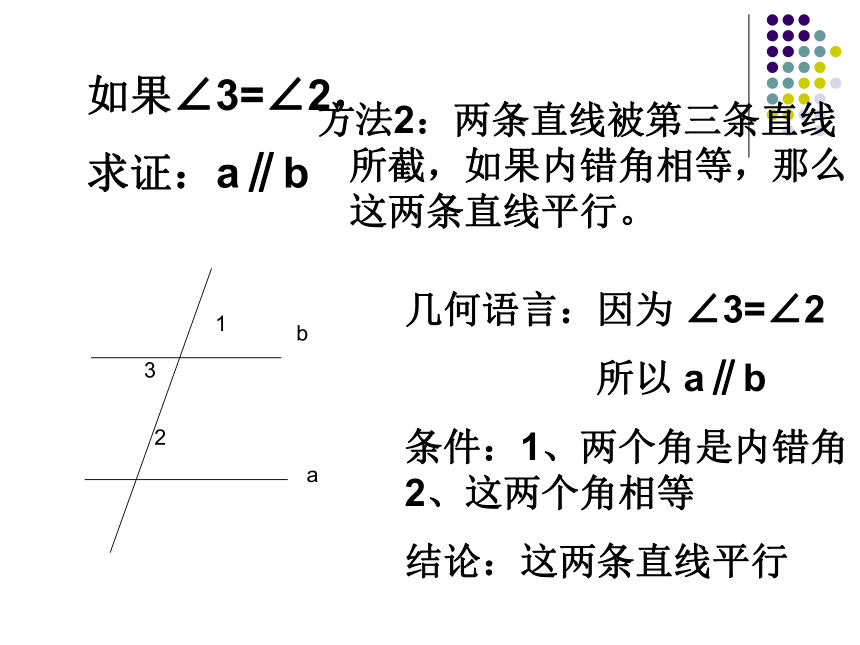
求证:AB∥DF,BC∥DE木工师傅常用角尺在长方体工件上画线,如图所画的直线CD、EF的位置关系怎样?为什么?想一想思考如图,如果∠2= ∠3,能得出a∥b吗?如果∠3=∠2,
求证:a∥b方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。几何语言:因为 ∠3=∠2
所以 a∥b
条件:1、两个角是内错角 2、这两个角相等
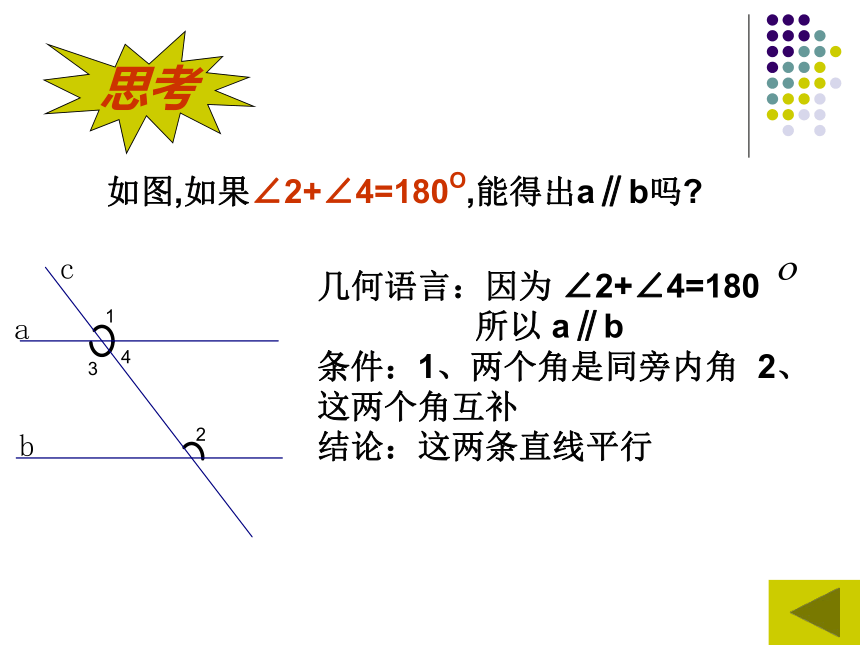
结论:这两条直线平行思考如图,如果∠2+∠4=180O,能得出a∥b吗?几何语言:因为 ∠2+∠4=180
所以 a∥b
条件:1、两个角是同旁内角 2、这两个角互补
结论:这两条直线平行两条直线平行的判定方法:方法1:两条直线被第三条直线所截,
如果同位角相等,那么这两条直线平行.方法2:两条直线被第三条直线所截,
如果内错角相等,那么这两条直线平行.方法3:两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行.1231、如图,根据图形完成下列推理过程:
(1)∵∠ABD=∠BDC(已知)
∴ ∥ ( )
(2)∵∠DBC=∠ADB(已知)
∴ ∥ ( )
(3)∵∠CBE=∠DCB(已知)
∴ ∥ ( )
(4)∵∠CBE=∠A(已知)
∴ ∥ ( )
(5)∵∠A+∠ADC=180O(已知)
∴ ∥ ( )2、两条直线被第三条直线所截,如果同位角相等,那么它们的内错角 ,同旁内角 ,这两条直线 。3、如果有两条直线被第三条直线所截,那么必定有 ( )
A 内错角相等 B 同位角相等
C 同旁内角互补 D 以上都不对4、如图,已知∠CAD=∠CBE,AF平分∠CAD,BG平分∠CBG,试问:AF与BG是否平行?为什么?5、如图,BE平分∠ABC,∠1=∠2,那么DE与BC的位置关系如何?6、如图,AB⊥BD于B,CD⊥BD于D,∠1+∠2=180O,则CD∥EF吗?为什么?7、如图,已知∠BED=∠B+∠D,试问:AB与CD平行吗?为什么?练习;1、已知∠1=60°,∠2=60°,则,a与b的关系
2、已知∠1=150°,∠2=30°,则,a与b的关系
3、已知∠1=52°,∠C= °,才能使AB∥CD(1)(2)(3)练习;1、已知∠1=60°,∠2=60°,则,a与b的关系
2、已知∠1=150°,∠2=30°,则,a与b的关系
3、已知∠1=52°,∠C= °,才能使AB∥CD例2:已知:∠1= ∠ 4, ∠1 +∠2=180°
求证:AB∥CD,AB∥EF例2:已知:∠1=140°,∠2=40°
求证:AB∥CD已知:∠1 +∠2= ∠2+∠3=180°
求证:a∥b,c∥d已知: ∠BAF=46°, ∠ACE=136°,CE⊥CD,求证:CD∥AB已知:∠C=∠D,∠D=∠1,
求证:AC∥DF,DB∥EC(四)、计算:
已知D是AB上一点,E是AC上一点, ADE=60°, B=60°, C=40°, 求 DEC 的度数。
(二)、判断:
1、两条直线被第三条直线所截,内错角相等.( )
2、同旁内角相等,两直线平行.( )(三)、填空:
(1) 2= (已知),
AC ED ( ).
(2) A + =180° (已知),
AB FD ( ).
ACBDEF123内错角相等,两直线平行 同旁内角互补,两直线平行╳╳DFCAFD2= 3.例2:已知:如图: BD平分 ABC,
1= 2 , C=70?, 求 DE BC 。 321AE D CBBD平分 ABC(已知),又 1= 2(已知),角平分线的定义内错角相等,两直线平行解:作业:P18 1,2,4
AB∥CD(简单说成:同位角相等,两直线平行.)结论:这两条直线平行条件:1、两个角是同位角2、这两个角相等(已知)例:∠B=90,DF⊥CB,DE⊥AB
求证:AB∥DF,BC∥DE木工师傅常用角尺在长方体工件上画线,如图所画的直线CD、EF的位置关系怎样?为什么?想一想思考如图,如果∠2= ∠3,能得出a∥b吗?如果∠3=∠2,
求证:a∥b方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。几何语言:因为 ∠3=∠2
所以 a∥b
条件:1、两个角是内错角 2、这两个角相等
结论:这两条直线平行思考如图,如果∠2+∠4=180O,能得出a∥b吗?几何语言:因为 ∠2+∠4=180
所以 a∥b
条件:1、两个角是同旁内角 2、这两个角互补
结论:这两条直线平行两条直线平行的判定方法:方法1:两条直线被第三条直线所截,
如果同位角相等,那么这两条直线平行.方法2:两条直线被第三条直线所截,
如果内错角相等,那么这两条直线平行.方法3:两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行.1231、如图,根据图形完成下列推理过程:
(1)∵∠ABD=∠BDC(已知)
∴ ∥ ( )
(2)∵∠DBC=∠ADB(已知)
∴ ∥ ( )
(3)∵∠CBE=∠DCB(已知)
∴ ∥ ( )
(4)∵∠CBE=∠A(已知)
∴ ∥ ( )
(5)∵∠A+∠ADC=180O(已知)
∴ ∥ ( )2、两条直线被第三条直线所截,如果同位角相等,那么它们的内错角 ,同旁内角 ,这两条直线 。3、如果有两条直线被第三条直线所截,那么必定有 ( )
A 内错角相等 B 同位角相等
C 同旁内角互补 D 以上都不对4、如图,已知∠CAD=∠CBE,AF平分∠CAD,BG平分∠CBG,试问:AF与BG是否平行?为什么?5、如图,BE平分∠ABC,∠1=∠2,那么DE与BC的位置关系如何?6、如图,AB⊥BD于B,CD⊥BD于D,∠1+∠2=180O,则CD∥EF吗?为什么?7、如图,已知∠BED=∠B+∠D,试问:AB与CD平行吗?为什么?练习;1、已知∠1=60°,∠2=60°,则,a与b的关系
2、已知∠1=150°,∠2=30°,则,a与b的关系
3、已知∠1=52°,∠C= °,才能使AB∥CD(1)(2)(3)练习;1、已知∠1=60°,∠2=60°,则,a与b的关系
2、已知∠1=150°,∠2=30°,则,a与b的关系
3、已知∠1=52°,∠C= °,才能使AB∥CD例2:已知:∠1= ∠ 4, ∠1 +∠2=180°
求证:AB∥CD,AB∥EF例2:已知:∠1=140°,∠2=40°
求证:AB∥CD已知:∠1 +∠2= ∠2+∠3=180°
求证:a∥b,c∥d已知: ∠BAF=46°, ∠ACE=136°,CE⊥CD,求证:CD∥AB已知:∠C=∠D,∠D=∠1,
求证:AC∥DF,DB∥EC(四)、计算:
已知D是AB上一点,E是AC上一点, ADE=60°, B=60°, C=40°, 求 DEC 的度数。
(二)、判断:
1、两条直线被第三条直线所截,内错角相等.( )
2、同旁内角相等,两直线平行.( )(三)、填空:
(1) 2= (已知),
AC ED ( ).
(2) A + =180° (已知),
AB FD ( ).
ACBDEF123内错角相等,两直线平行 同旁内角互补,两直线平行╳╳DFCAFD2= 3.例2:已知:如图: BD平分 ABC,
1= 2 , C=70?, 求 DE BC 。 321AE D CBBD平分 ABC(已知),又 1= 2(已知),角平分线的定义内错角相等,两直线平行解:作业:P18 1,2,4
