余角和补角[下学期]
图片预览



文档简介
课件11张PPT。3.4.2
余
角
和
补
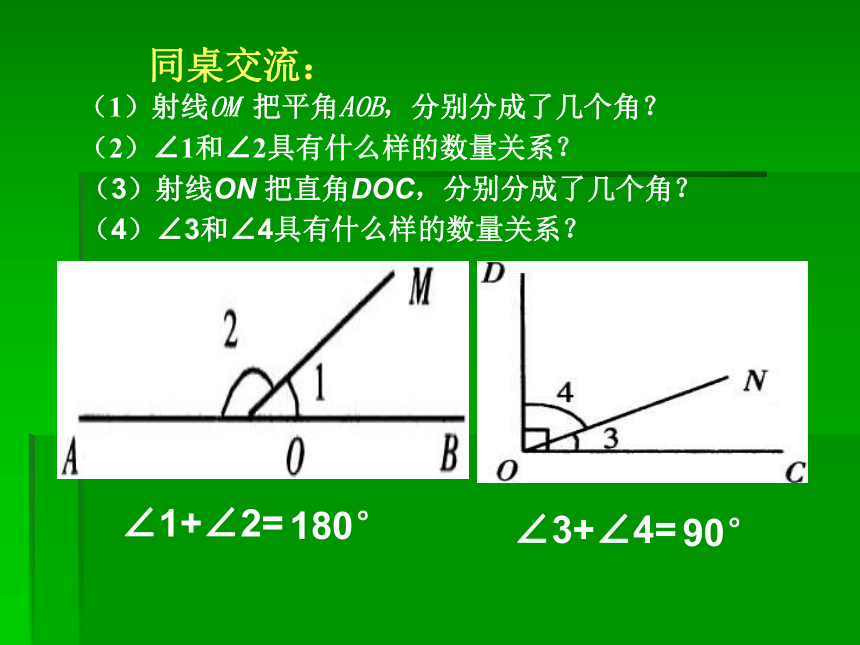
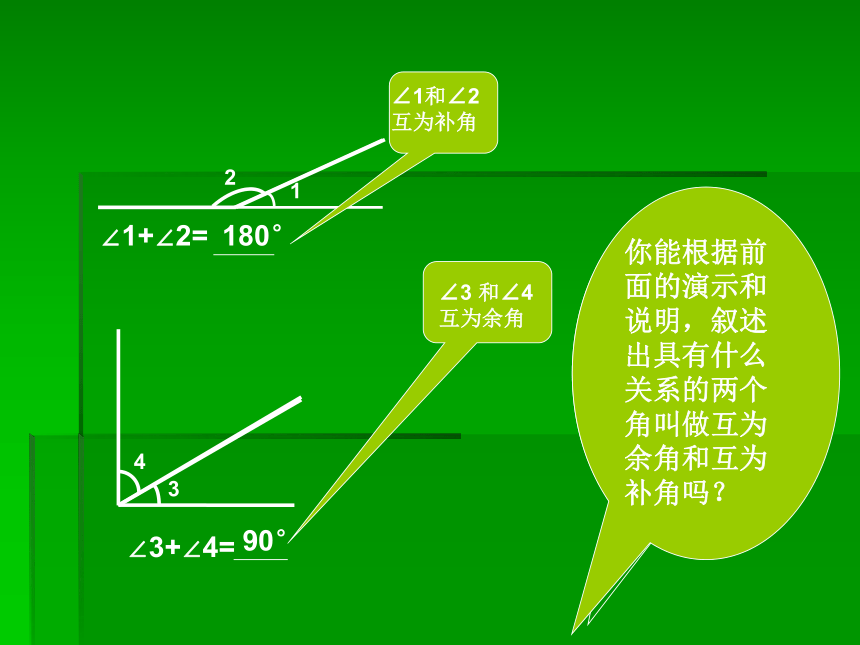
角3.4.2 余角和补角 打台球时,我们会选择适当的方向用白球击打红球,反弹后的红球会直接入袋。 这里蕴涵着哪些数学知识呢?同桌交流:(1)射线OM 把平角AOB,分别分成了几个角? (2)∠1和∠2具有什么样的数量关系? (3)射线ON 把直角DOC,分别分成了几个角? (4)∠3和∠4具有什么样的数量关系?90°180°互为余角、互为补角的定义 :1.互为余角的定义 :如果两个角的和是一个直角(等于 90°),那么这两个角叫互为余角,简称互余.其中一个角叫做另一个角的余角.2.互为补角的定义 :如果两个角的和是一个平角(等于180°),那么这两个角叫互为补角,简称互补.其中一个角叫做另一个角的补角.问题1:以上定义中的“互为”是什么意思?问题3:互为余角、互为补角的两个角是否一定有公共顶点、公共边?
1.若∠1=35°, ∠2=55°,则∠1是∠2的 ,也可以说∠2是∠1的 ;
若∠1=135°, ∠2=45°,则∠1是∠2的 ,也可以说∠2是∠1的 。
2.若∠1和∠2的互为余角,则∠1+∠2= , ∠1= —∠2, ∠2=
—∠1;
若∠1和∠2的互为补角,则∠1+∠2= , ∠1= —∠2, ∠2=
—∠1。
3.若∠α 和∠ β 互余,且∠α=37°,则∠β=
若∠α和∠β互补,且∠β=126°,则∠α=
余角余角补角补角90°90°90°180°180°180°53°54°试一试:比一比: 判断:
1.锐角的余角是锐角,锐角的补角是钝角。( )
2.钝角没有余角,但有补角,其补角是锐角。( )
3.一个角的补角一定是钝角。( )
4.一个角的补角一定比这个角大。( )
5.两个互补的角中一定有一个是钝角。( )
6.相等且互补的两个角都是直角。( )1.一个角是70°,则它的余角的补角是
2.一个角的补角是150°,则这个角的余角是
3.一个角的补角是它的3倍,则这个角是160°60°45°点击中考:实践操练:如图,要测量两堵围墙所形成的角AOB的度数,但人不能进入围墙,如何测量?C与你的学习伙伴们讨论讨论 课堂小结:学习了本节课你有哪些收获?作业:课本:140页10题3.4.2 余角和补角一.导课 三.试一试、比一
台球桌上的数学问题 比、点击中考、
二.概念 实践操练……
1.互为余角: 四.小结……
两个角的和是90° ……五.作业……
2.互为补角:
两个角的和是180°…… 如图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,34
余
角
和
补
角3.4.2 余角和补角 打台球时,我们会选择适当的方向用白球击打红球,反弹后的红球会直接入袋。 这里蕴涵着哪些数学知识呢?同桌交流:(1)射线OM 把平角AOB,分别分成了几个角? (2)∠1和∠2具有什么样的数量关系? (3)射线ON 把直角DOC,分别分成了几个角? (4)∠3和∠4具有什么样的数量关系?90°180°互为余角、互为补角的定义 :1.互为余角的定义 :如果两个角的和是一个直角(等于 90°),那么这两个角叫互为余角,简称互余.其中一个角叫做另一个角的余角.2.互为补角的定义 :如果两个角的和是一个平角(等于180°),那么这两个角叫互为补角,简称互补.其中一个角叫做另一个角的补角.问题1:以上定义中的“互为”是什么意思?问题3:互为余角、互为补角的两个角是否一定有公共顶点、公共边?
1.若∠1=35°, ∠2=55°,则∠1是∠2的 ,也可以说∠2是∠1的 ;
若∠1=135°, ∠2=45°,则∠1是∠2的 ,也可以说∠2是∠1的 。
2.若∠1和∠2的互为余角,则∠1+∠2= , ∠1= —∠2, ∠2=
—∠1;
若∠1和∠2的互为补角,则∠1+∠2= , ∠1= —∠2, ∠2=
—∠1。
3.若∠α 和∠ β 互余,且∠α=37°,则∠β=
若∠α和∠β互补,且∠β=126°,则∠α=
余角余角补角补角90°90°90°180°180°180°53°54°试一试:比一比: 判断:
1.锐角的余角是锐角,锐角的补角是钝角。( )
2.钝角没有余角,但有补角,其补角是锐角。( )
3.一个角的补角一定是钝角。( )
4.一个角的补角一定比这个角大。( )
5.两个互补的角中一定有一个是钝角。( )
6.相等且互补的两个角都是直角。( )1.一个角是70°,则它的余角的补角是
2.一个角的补角是150°,则这个角的余角是
3.一个角的补角是它的3倍,则这个角是160°60°45°点击中考:实践操练:如图,要测量两堵围墙所形成的角AOB的度数,但人不能进入围墙,如何测量?C与你的学习伙伴们讨论讨论 课堂小结:学习了本节课你有哪些收获?作业:课本:140页10题3.4.2 余角和补角一.导课 三.试一试、比一
台球桌上的数学问题 比、点击中考、
二.概念 实践操练……
1.互为余角: 四.小结……
两个角的和是90° ……五.作业……
2.互为补角:
两个角的和是180°…… 如图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,34
