1.3 探索三角形全等的条件 第2课时 课件(共48张PPT) 2023-2024学年苏科版数学八年级上册
文档属性
| 名称 | 1.3 探索三角形全等的条件 第2课时 课件(共48张PPT) 2023-2024学年苏科版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 00:00:00 | ||
图片预览






文档简介
(共48张PPT)
1 . 3
探索三角形全等的条件
第2课时
利用两角一边判定三角形全等
讨 论
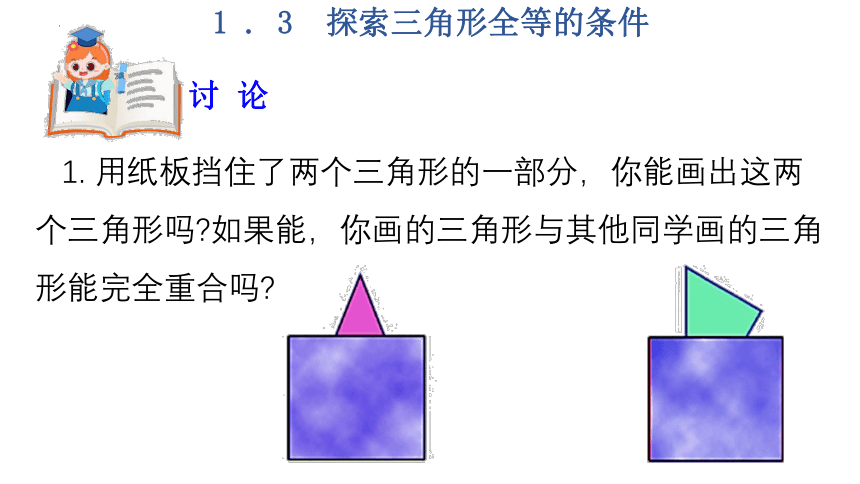
1. 用纸板挡住了两个三角形的一部分,你能画出这两个三角形吗 如果能,你画的三角形与其他同学画的三角形能完全重合吗
第一个不能,因为第一个图中的三角形只确定了一个角,其他边与角大小不确定;
第二个能,因为第二个三角形确定了两角及其夹边的大小,所以这个三角形的形状与大小就确定了,即只需往下延长左右两边的线段就得到第三个顶点.
画的二角形能完全重合.
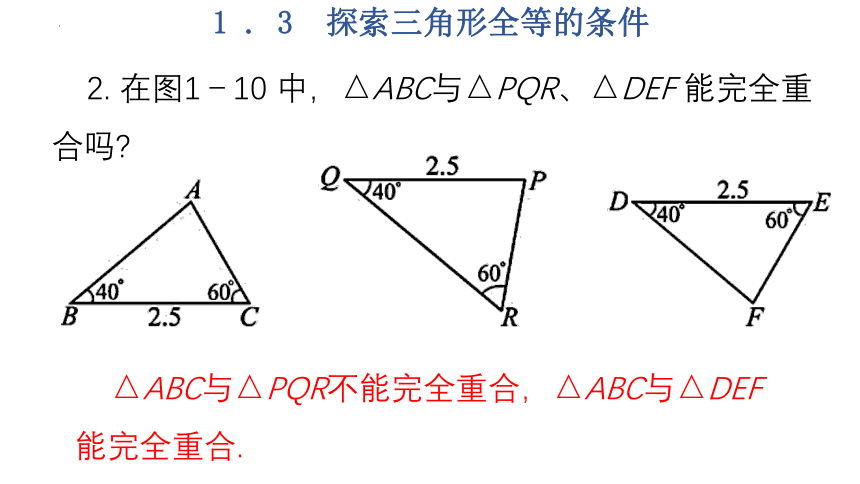
2. 在图1-10 中,△ABC与△PQR、△DEF 能完全重合吗
△ABC与△PQR不能完全重合,△ABC与△DEF 能完全重合.
操 作
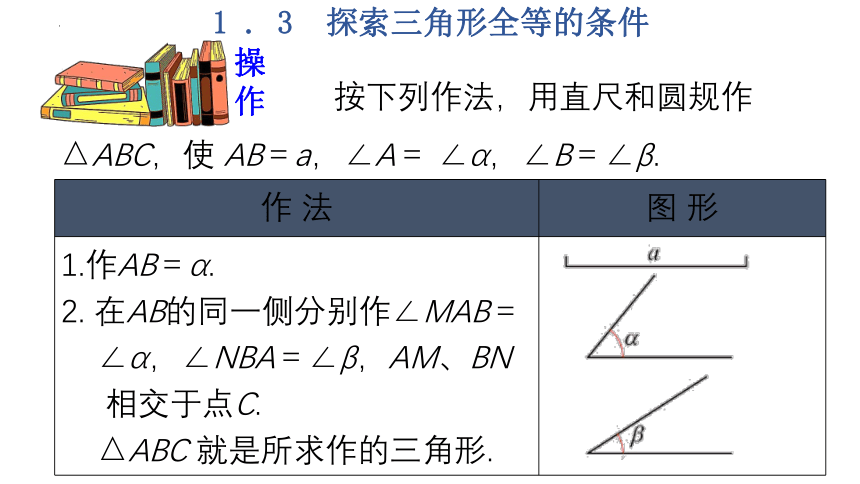
按下列作法,用直尺和圆规作△ABC,使 AB=a,∠A= ∠α,∠B=∠β.
作 法 图 形
1.作AB=α. 2. 在AB的同一侧分别作∠MAB= ∠α,∠NBA=∠β,AM、BN 相交于点C. △ABC 就是所求作的三角形.
你作的三角形与其他同学作的三角形能完全重合吗
实践告诉我们判定两个三角形全等的又一个基本事实:
两角及其夹边分别相等的两个三角形全等 (可以简写成“角边角”或“ASA”).
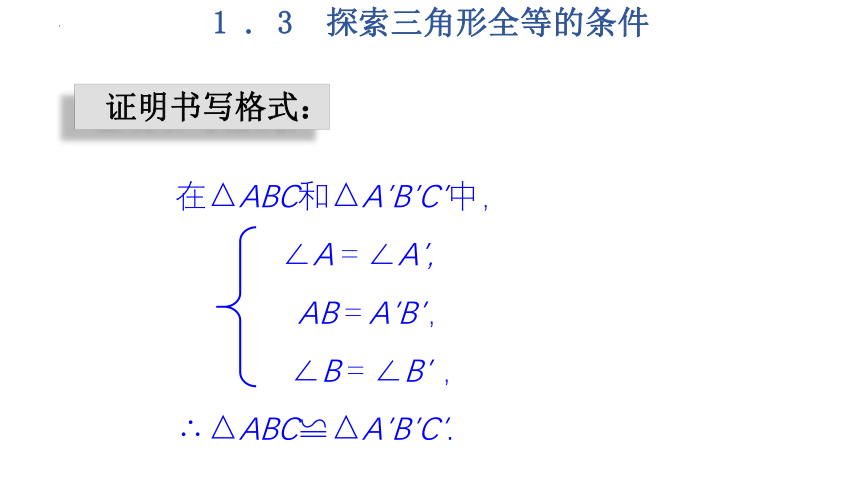
证明书写格式:
在△ABC和△A′B′C′中,
∠A=∠A′,
AB=A′B′,
∠B=∠B′ ,∴△ABC≌△A′B′C′.
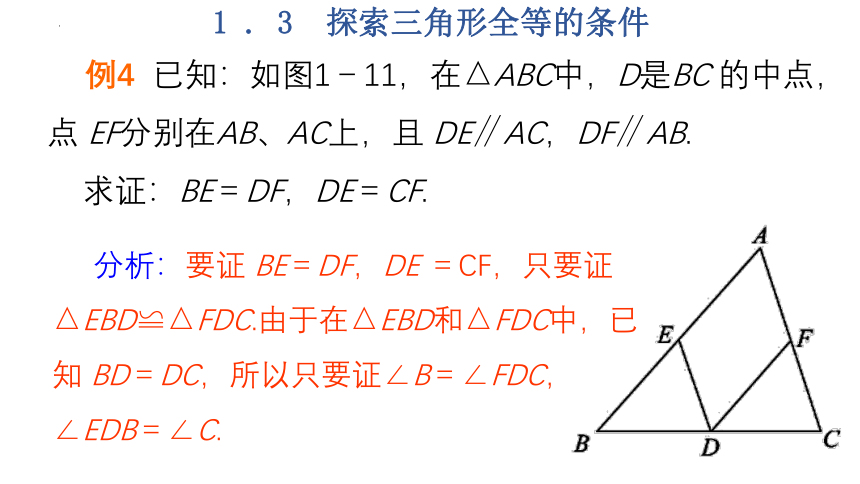
例4 已知:如图1-11,在△ABC中,D是BC 的中点,点 EF分别在AB、AC上,且 DE∥AC,DF∥AB.
求证:BE=DF,DE=CF.
分析:要证 BE=DF,DE =CF,只要证△EBD≌△FDC.由于在△EBD和△FDC中,已知 BD=DC,所以只要证∠B=∠FDC,∠EDB=∠C.
证明:∵DE//AC,DF// AB(已知),
∴∠EDB=∠C,∠B=∠FDC
(两直线平行,同位角相等).
∵D 是 BC 的中点(已知),
∴BD=DC(线段中点的定义).
在△EBD 和△FDC 中,
∠EDB=∠C (已证).
BD=DC (已证),
∠B=∠FDC (已证),
∴△EBD ≌△FDC (ASA).
∴ BE=DF,DE=CF
(全等三角形的对应边相等).
练2
已知:如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:AD=AE.
分析:证明△ACD≌△ABE中,就可以得出 AD=AE.
AC=AB ,
∠C=∠B ,
∴△ACD≌△ABE (ASA).
∴AD=AE.
∠A=∠A (公共角),
证明:在△ACD和△ABE中,
练 习
1. 找出图中的全等三角形,并说明理由.
解:图中全等二角形共有三组:
(1) ①与⑥全等.
理由如下:在△ABC 和△MNG 中,
∠A=∠M,
AB=MN,
∠B=∠N,
∴△ABC ≌ △MNG(ASA).
(2) ②与④全等.
理由如下:
在△TSW中,∠S=180°-70°-50°=60°,
∴∠S=∠Y.
在△XYZ 和△TSW中,
∴△ XYZ ≌ △TSW (ASA).
∠Y=∠S,
ZY=WS,
∠Z=∠W,
(3) ③与⑤全等.
理由如下:
在△RQP 和△DEF 中,
∠R=∠D,
PR=FD,
∠P=∠F,
∴△RQP ≌ △DEF (ASA).
2. 已知:如图,AB、CD相交于点 O,O是AB的中点,
AC//BD.
求证:O是CD的中点.
证明:∵O是AB的中点(已知),
∴OA=OB(线段中点的定义).
∵AC∥BD (已知),
∴∠A=∠B (两直线平行,内错角相等).
在△AOC 和△BOD中,
∠A=∠B(已证),
OA=OB(已证),
∠AOC=∠BOD (对顶角相等),
∴ △AOC ≌ △BOD (ASA).
∴ OC=OD (全等三角形的对应边相等),
即O是CD的中点.
讨 论
如图1-12,在△ABC 和△MNP 中,∠A=∠M,∠B =∠N,BC=NP. △ABC与△MNP 全等吗 为什么
由三角形内角和定理可知∠C=∠P.
根据“ASA”可以证明△ABC ≌△MNP.
由此可以得到基本事实 (ASA) 的推论:
两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”).
例5 已知:如图1-13,△ABC≌△A′B′C′,AD、A′D′分别是△ABC 和△A′B′C′的高.
求证:AD=A′D′.
分析:要证 AD=A′D′,只要证 △ABD⊥△A′B′D′. 由于在△ABD和△A′B′D′中,∠ADB -∠A′D′B′=90°,所以只要证 AB=A′B′,∠B=∠B′.
证明:∵△ABC≌△A′B′C′(已知),
∴ AB=A′B′,∠B=∠B′
(全等三角形的对应边相等、
对应角相等).
∵ AD、A′D′分别是△ABC和
△A′B′C′的高(已知),
∴ ∠ADB=∠A′D′B′=90°.
在△ABD 和△A′B′D′中,
∠B=∠B′(已证),
∠ADB = ∠A′D′B′(已证),
AB=A′B′(已证),
∴△ABD ≌ △A′B′D′(AAS).
∴AD=AD
(全等三角形的对应边相等).
练3
如图,AD是△ABC的中线,过C,B分别作AD及AD的延长线的垂线CF,BE.
求证:BE=CF.
导引:要证明BE=CF,可根据中线及垂线的定义和对顶角的性质来证明△BDE和△CDF全等.
证明:∵AD是△ABC的中线,
∴BD=CD.
∵CF⊥AD,BE⊥AE,
∴∠CFD=∠BED=90°.
在△BDE和△CDF中,
∠BED=∠CFD,
∠BDE=∠CDF,
BD=CD,
∴ △BDE≌△CDF(AAS).
∴ BE=CF.
讨 论
在图1-13中,如果 AD、A′D′分别是△ABC和△A′B′C′的角平分线(或中线),那么AD与A′D′相等吗 试证明你的结论.
练 习
1. 已知: 如图,∠A=∠D,∠ACB=∠DBC.
求证:AB=DC.
证明:在△ABC 和△DCB 中,
∠A=∠D(已知),
∠ACB=∠DBC(已知),
BC=CB(公共边),
∴△ABC≌△DCB(AAS)
∴AB=DC(全等三角形的对应边相等).
2. 已知:如图,CB⊥AD,AE⊥DC,垂足分别为 B、E,
AE、BC 相交于点F,且AB=BC.
求证:△ABF≌△CBD.
证明:∵CB⊥AD,AE⊥DC(已知),
∴∠ABF=∠CBD
=∠AED=90°
(垂直的定义).
∴∠A+∠D=90°,∠C+∠D=90°
(直角三角形的两个锐角互余).
∴∠A=∠C (同角的余角相等).
在△ABF 和△CBD 中,
∠A=∠C(已证)
AB=CB(已知),
∠ABF=∠CBD(已证)
∴△ABF≌△CBD(ASA)
讨 论
1. 如图1-14,∠A=∠B,∠1=∠2,EA=EB. 你能证
明 AC=BD 吗
能
2. 如图1-15,点C、F在AD上,且AF=DC,∠B=∠E,
∠A=∠D. 你能证明AB=DE 吗
能
例6 已知:如图1-16,点A、B、C、D 在一条直线上,EA ∥FB,EC∥FD,EA=FB.
求证:AB=CD.
分析:要证 AB=CD,只要证 AB+BC=CD+BC,即AC=BD,所以只要证 △EAC≌△FBD.
证明:∵EA∥FB,EC∥FD(已知),
∴∠A=∠FBD,∠ECA=∠D
(两直线平行,同位角相等)
在△EAC和△FBD中,
∠A=∠FBD(已证),
∠ECA=∠D(已证),
EA=FB(已知),
∴△EAC≌△FBD(AAS).
∴ AC=BD
(全等三角形的对应边相等),
即 AB+BC =CD+BC.
∴ AB=CD
(等式的性质).
上面的推理过程可以用符号“=>”简明地表述如下:
EA∥FB => ∠A =∠FBD
EC∥FD => ∠ECA=∠D => △AEA≌△FBD
EA = FB
=> AB+BC = CD+BC => AB=CD
=> AC=BD
练 习
1. 已知:如图,AB=AC,点 D、E分别在AB、AC 上,
∠1 =∠2 .
求证:DB=EC.
2. 已知: 如图,∠ABC =∠DCB,∠1=∠2.
求证:AB=DC.
本课小结
全等三角形
利用两角一边判定,三角形全等
两角及其夹边
(ASA)
两角和其中一角的对边(AAS)
1 . 3
探索三角形全等的条件
第2课时
利用两角一边判定三角形全等
讨 论
1. 用纸板挡住了两个三角形的一部分,你能画出这两个三角形吗 如果能,你画的三角形与其他同学画的三角形能完全重合吗
第一个不能,因为第一个图中的三角形只确定了一个角,其他边与角大小不确定;
第二个能,因为第二个三角形确定了两角及其夹边的大小,所以这个三角形的形状与大小就确定了,即只需往下延长左右两边的线段就得到第三个顶点.
画的二角形能完全重合.
2. 在图1-10 中,△ABC与△PQR、△DEF 能完全重合吗
△ABC与△PQR不能完全重合,△ABC与△DEF 能完全重合.
操 作
按下列作法,用直尺和圆规作△ABC,使 AB=a,∠A= ∠α,∠B=∠β.
作 法 图 形
1.作AB=α. 2. 在AB的同一侧分别作∠MAB= ∠α,∠NBA=∠β,AM、BN 相交于点C. △ABC 就是所求作的三角形.
你作的三角形与其他同学作的三角形能完全重合吗
实践告诉我们判定两个三角形全等的又一个基本事实:
两角及其夹边分别相等的两个三角形全等 (可以简写成“角边角”或“ASA”).
证明书写格式:
在△ABC和△A′B′C′中,
∠A=∠A′,
AB=A′B′,
∠B=∠B′ ,∴△ABC≌△A′B′C′.
例4 已知:如图1-11,在△ABC中,D是BC 的中点,点 EF分别在AB、AC上,且 DE∥AC,DF∥AB.
求证:BE=DF,DE=CF.
分析:要证 BE=DF,DE =CF,只要证△EBD≌△FDC.由于在△EBD和△FDC中,已知 BD=DC,所以只要证∠B=∠FDC,∠EDB=∠C.
证明:∵DE//AC,DF// AB(已知),
∴∠EDB=∠C,∠B=∠FDC
(两直线平行,同位角相等).
∵D 是 BC 的中点(已知),
∴BD=DC(线段中点的定义).
在△EBD 和△FDC 中,
∠EDB=∠C (已证).
BD=DC (已证),
∠B=∠FDC (已证),
∴△EBD ≌△FDC (ASA).
∴ BE=DF,DE=CF
(全等三角形的对应边相等).
练2
已知:如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:AD=AE.
分析:证明△ACD≌△ABE中,就可以得出 AD=AE.
AC=AB ,
∠C=∠B ,
∴△ACD≌△ABE (ASA).
∴AD=AE.
∠A=∠A (公共角),
证明:在△ACD和△ABE中,
练 习
1. 找出图中的全等三角形,并说明理由.
解:图中全等二角形共有三组:
(1) ①与⑥全等.
理由如下:在△ABC 和△MNG 中,
∠A=∠M,
AB=MN,
∠B=∠N,
∴△ABC ≌ △MNG(ASA).
(2) ②与④全等.
理由如下:
在△TSW中,∠S=180°-70°-50°=60°,
∴∠S=∠Y.
在△XYZ 和△TSW中,
∴△ XYZ ≌ △TSW (ASA).
∠Y=∠S,
ZY=WS,
∠Z=∠W,
(3) ③与⑤全等.
理由如下:
在△RQP 和△DEF 中,
∠R=∠D,
PR=FD,
∠P=∠F,
∴△RQP ≌ △DEF (ASA).
2. 已知:如图,AB、CD相交于点 O,O是AB的中点,
AC//BD.
求证:O是CD的中点.
证明:∵O是AB的中点(已知),
∴OA=OB(线段中点的定义).
∵AC∥BD (已知),
∴∠A=∠B (两直线平行,内错角相等).
在△AOC 和△BOD中,
∠A=∠B(已证),
OA=OB(已证),
∠AOC=∠BOD (对顶角相等),
∴ △AOC ≌ △BOD (ASA).
∴ OC=OD (全等三角形的对应边相等),
即O是CD的中点.
讨 论
如图1-12,在△ABC 和△MNP 中,∠A=∠M,∠B =∠N,BC=NP. △ABC与△MNP 全等吗 为什么
由三角形内角和定理可知∠C=∠P.
根据“ASA”可以证明△ABC ≌△MNP.
由此可以得到基本事实 (ASA) 的推论:
两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”).
例5 已知:如图1-13,△ABC≌△A′B′C′,AD、A′D′分别是△ABC 和△A′B′C′的高.
求证:AD=A′D′.
分析:要证 AD=A′D′,只要证 △ABD⊥△A′B′D′. 由于在△ABD和△A′B′D′中,∠ADB -∠A′D′B′=90°,所以只要证 AB=A′B′,∠B=∠B′.
证明:∵△ABC≌△A′B′C′(已知),
∴ AB=A′B′,∠B=∠B′
(全等三角形的对应边相等、
对应角相等).
∵ AD、A′D′分别是△ABC和
△A′B′C′的高(已知),
∴ ∠ADB=∠A′D′B′=90°.
在△ABD 和△A′B′D′中,
∠B=∠B′(已证),
∠ADB = ∠A′D′B′(已证),
AB=A′B′(已证),
∴△ABD ≌ △A′B′D′(AAS).
∴AD=AD
(全等三角形的对应边相等).
练3
如图,AD是△ABC的中线,过C,B分别作AD及AD的延长线的垂线CF,BE.
求证:BE=CF.
导引:要证明BE=CF,可根据中线及垂线的定义和对顶角的性质来证明△BDE和△CDF全等.
证明:∵AD是△ABC的中线,
∴BD=CD.
∵CF⊥AD,BE⊥AE,
∴∠CFD=∠BED=90°.
在△BDE和△CDF中,
∠BED=∠CFD,
∠BDE=∠CDF,
BD=CD,
∴ △BDE≌△CDF(AAS).
∴ BE=CF.
讨 论
在图1-13中,如果 AD、A′D′分别是△ABC和△A′B′C′的角平分线(或中线),那么AD与A′D′相等吗 试证明你的结论.
练 习
1. 已知: 如图,∠A=∠D,∠ACB=∠DBC.
求证:AB=DC.
证明:在△ABC 和△DCB 中,
∠A=∠D(已知),
∠ACB=∠DBC(已知),
BC=CB(公共边),
∴△ABC≌△DCB(AAS)
∴AB=DC(全等三角形的对应边相等).
2. 已知:如图,CB⊥AD,AE⊥DC,垂足分别为 B、E,
AE、BC 相交于点F,且AB=BC.
求证:△ABF≌△CBD.
证明:∵CB⊥AD,AE⊥DC(已知),
∴∠ABF=∠CBD
=∠AED=90°
(垂直的定义).
∴∠A+∠D=90°,∠C+∠D=90°
(直角三角形的两个锐角互余).
∴∠A=∠C (同角的余角相等).
在△ABF 和△CBD 中,
∠A=∠C(已证)
AB=CB(已知),
∠ABF=∠CBD(已证)
∴△ABF≌△CBD(ASA)
讨 论
1. 如图1-14,∠A=∠B,∠1=∠2,EA=EB. 你能证
明 AC=BD 吗
能
2. 如图1-15,点C、F在AD上,且AF=DC,∠B=∠E,
∠A=∠D. 你能证明AB=DE 吗
能
例6 已知:如图1-16,点A、B、C、D 在一条直线上,EA ∥FB,EC∥FD,EA=FB.
求证:AB=CD.
分析:要证 AB=CD,只要证 AB+BC=CD+BC,即AC=BD,所以只要证 △EAC≌△FBD.
证明:∵EA∥FB,EC∥FD(已知),
∴∠A=∠FBD,∠ECA=∠D
(两直线平行,同位角相等)
在△EAC和△FBD中,
∠A=∠FBD(已证),
∠ECA=∠D(已证),
EA=FB(已知),
∴△EAC≌△FBD(AAS).
∴ AC=BD
(全等三角形的对应边相等),
即 AB+BC =CD+BC.
∴ AB=CD
(等式的性质).
上面的推理过程可以用符号“=>”简明地表述如下:
EA∥FB => ∠A =∠FBD
EC∥FD => ∠ECA=∠D => △AEA≌△FBD
EA = FB
=> AB+BC = CD+BC => AB=CD
=> AC=BD
练 习
1. 已知:如图,AB=AC,点 D、E分别在AB、AC 上,
∠1 =∠2 .
求证:DB=EC.
2. 已知: 如图,∠ABC =∠DCB,∠1=∠2.
求证:AB=DC.
本课小结
全等三角形
利用两角一边判定,三角形全等
两角及其夹边
(ASA)
两角和其中一角的对边(AAS)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
